SQLで最急降下する

信州大学 kstm Advent Calendar 2018の4日目です

最近BigQueryやSQLServerに機械学習系のアルゴリズムが追加されてますね．
今回はSQLの再帰クエリを使って最急降下して遊びました．

最急降下法

関数$f(x)$について，以下の更新式で極値となるパラメータの値を求めます．

$$
x \leftarrow x - \eta \frac{\partial\mathcal{f}}{\partial x}
$$

ためしにSQLで次の関数を最小化してみましょう．

$$
y(x) = x^2 - 6x + 9
$$

$y' = 2x - 6$，学習率を$\eta=0.01$とするとこんなかんじ

with
    recursive gd(iter, x, y) as (
        select
            0, cast(0.0 as decimal(6,3)), cast(9 as decimal(6,3))
        union all
        select
            iter+1, x-0.01*(2.0*x-6.0), pow(x-0.01*(2.0*x-6.0),2)-6*(x-0.01*(2.0*x-6.0)) + 9 
        from
            gd
        where
            iter < 1000
            and y - (pow(x-0.1*(2.0*x-6.0),2)-6*(x-0.1*(2.0*x-6.0)) + 9) > 0.001
    )
select * from gd order by iter desc limit 1

結果は．．．

iter	x	y
197	2.941	0.003

できた！

線形回帰もやってみる

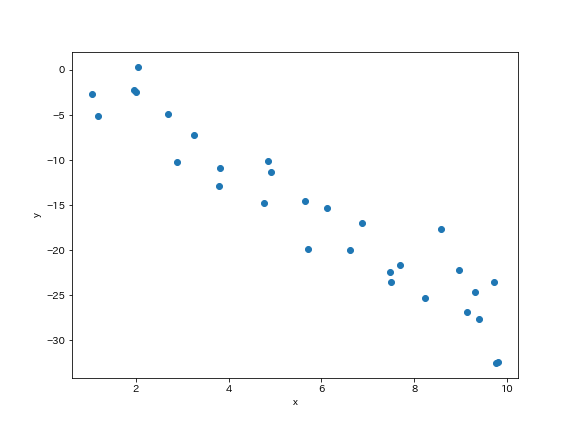
$y \sim \mathcal{N}(a + bx, \sigma)$のようなデータを適当に作っておきます．
ここでは$a=1, b=-3$にしました．

誤差関数と更新式は以下．
$$ \mathcal{L} = \frac{1}{2N} \sum_{i=1}^{N}(a+bx_i-y_i)^2 $$

\begin{align}
\frac{\partial\mathcal{L}}{\partial a} &= \frac{1}{N} \sum_{i=1}^{N}(a+bx_i-y_i) \\
\frac{\partial\mathcal{L}}{\partial b} &= \frac{1}{N} \sum_{i=1}^{N}(a+bx_i-y_i)x_i
\end{align}

学習率$\eta=0.01$で，誤差の変化が$0.01$以下になったら終了するようにしました．

with
    recursive agg as (
        select
            sum(x) s_x,
            sum(y) s_y,
            sum(x*x) s_x2,
            sum(y*y) s_y2,
            sum(x*y) s_xy,
            count(*) n
        from lr
    ),
    gd(iter, a, b, loss) as (
        select
            0, cast(1.0 as decimal(10, 5)), cast(1.0 as decimal(10, 5)), cast(100.0 as decimal(10, 5))
        from lr
        union all
        select
            iter+1,
            a-0.01*(n*a+b*s_x-s_y)/n,
            b-0.01*(a*s_x+b*s_x2-s_xy)/n,
            (n*pow(a-0.01*(n*a+b*s_x-s_y)/n,2)
             +pow(b-0.01*(a*s_x+b*s_x2-s_xy),2)*s_x2
             +s_y2
             +2*(a-0.01*(n*a+b*s_x-s_y)/n)*(b-0.01*(a*s_x+b*s_x2-s_xy))*s_x
             -2*(a-0.01*(n*a+b*s_x-s_y)/n)*s_y
             -2*(b-0.01*(a*s_x+b*s_x2-s_xy))*s_xy)/(2*n)
        from
            gd, agg
        where
            iter < 5000
            and loss > 0.1
            and abs(
                loss-(n*pow(a-0.01*(n*a+b*s_x-s_y)/n,2)
                +pow(b-0.01*(a*s_x+b*s_x2-s_xy),2)*s_x2
                +s_y2
                +2*(a-0.01*(n*a+b*s_x-s_y)/n)*(b-0.01*(a*s_x+b*s_x2-s_xy))*s_x
                -2*(a-0.01*(n*a+b*s_x-s_y)/n)*s_y
                -2*(b-0.01*(a*s_x+b*s_x2-s_xy))*s_xy)/(2*n)) > 0.01
    )
select * from gd order by iter desc limit 1

結果はこちら

iter	a	b	loss
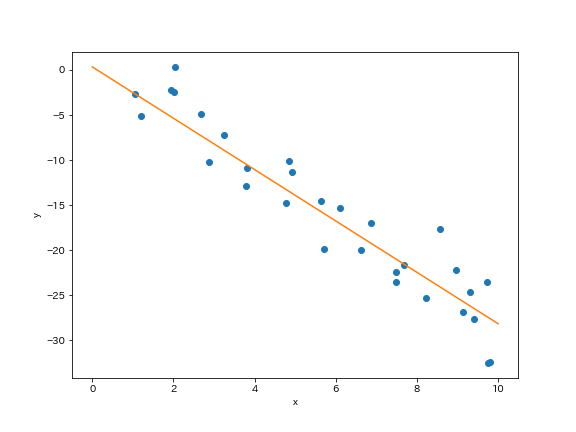
18	0.34115	-2.84881	3.31067

いいかんじですね．

今回の実装を実行したnotebookはこちらです．