Boidsモデルで魚の群れの動きを再現する

概要

群れの動きを表現するモデルとして、Boidsモデルというものがある。

群体を構成する一つ一つの個体に対して、以下のルールを適用することで、群体としての動きを再現できる、というもの。

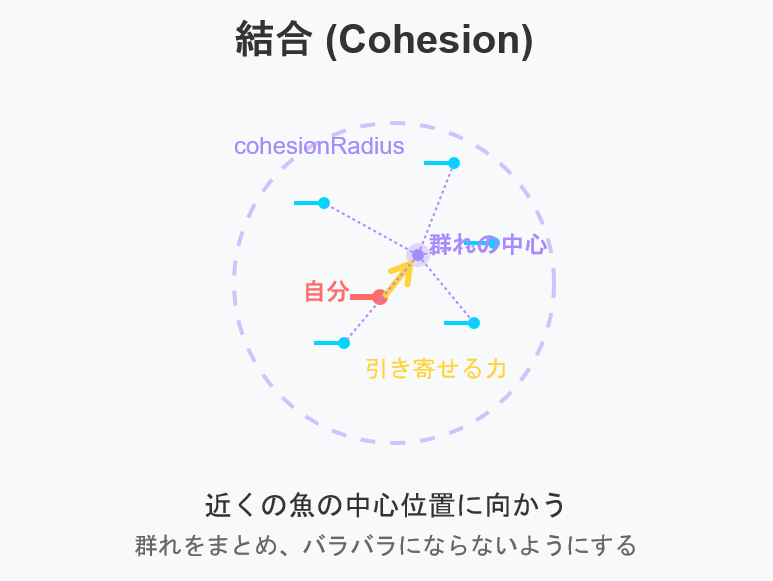
• 結合（Cohesion）
  • オブジェクトが他のオブジェクトが集まっている群れの中心方向へ向かうように方向を変える。
• 分離（Separation）
  • オブジェクトが他のオブジェクトとぶつからないように距離をとる。
• 整列（Alignment）
  • オブジェクトが他のオブジェクトと概ね同じ方向に飛ぶように速度と方向を合わせる。

群れ全体に対する記述ではなく、個々の魚の挙動に対する言及である点がポイント。
各々の魚が上記の原理に従って動くだけで、全体として群体っぽい動き（水族館で見るイワシの群れみたいな動き）を再現できる。 　

今回は、簡単に以下の技術スタックで実装する。

• HTML5 Canvas
• Vanilla JavaScript

完成イメージは以下。

Boidsモデルについて

Boidsモデルについて、もう少し詳しく整理する。
各々の魚は上述の３つの力（結合・分離・整列）の影響を受けて、自身の速度ベクトルを刻々と変化させる。それぞれの力について以下に整理する。

※文字通り(物理の文脈における)「力」(≒加速度)である。つまり、次の時刻における速度$\boldsymbol{v}(t + dt) = \boldsymbol{v}(t) + \frac{\boldsymbol{F}_{net}}{m} dt$ を計算するための材料とする。

結合（Cohesion）

群れの中心に引き寄せられる方向に力を受ける。群れの中心が離れているほど強く力を受ける。

🐠「なるべくみんなといっしょにいたい」
群れのぬくもり。

自分の周囲にいる魚たちの群れの中心の座標を計算し、自分の座標から見た位置ベクトルを結合ベクトル $\boldsymbol{F}_{coh}$とする。

\boldsymbol{F}_{coh} =  \left( \frac{1}{n} \sum_{範囲内} \boldsymbol{r} \right) - \boldsymbol{r_0}

実装は以下。

    /**
     * Cohesion (結合): 近くの魚の中心に向かう
     * @param {Fish[]} allFish - すべての魚の配列
     * @returns {{x: number, y: number}} 結合のための力ベクトル
     */
    cohesion(allFish) {
        let centerX = 0;
        let centerY = 0;
        let count = 0;

        for (let other of allFish) {
            if (other === this) continue;

            const distance = this.distanceTo(other);

            // 一定距離内の魚の位置を平均する
            if (distance > 0 && distance < this.cohesionRadius) {
                centerX += other.x;
                centerY += other.y;
                count++;
            }
        }

        if (count > 0) {
            centerX /= count;
            centerY /= count;

            // 中心に向かう方向ベクトル
            return {
                x: centerX - this.x,
                y: centerY - this.y
            };
        }

        return { x: 0, y: 0 };
    }

分離（Separation）

他の魚とぶつからないように距離をとる。
🐠「みんなといっしょにいたいけどパーソナルスペースは守りたい。」
ATフィールド。

他の魚との距離が近いほど、強く反発する方向に力を受ける。距離(の1乗)に反比例して力を受けるものとする。
この反発を表すベクトルをすべての魚に対して計算し、総和を取ったものを分離ベクトル $\boldsymbol{F}_{sep}$ とする。
つまり以下を分離ベクトルとする。

\boldsymbol{F}_{sep} = \frac{1}{n} \sum_{範囲内} - \frac{\boldsymbol{r}-\boldsymbol{r_0}}{ | \boldsymbol{r}-\boldsymbol{r_0} |^2 }

実装は以下。

    /**
     * Separation (分離): 近くの魚から離れる
     * @param {Fish[]} allFish - すべての魚の配列
     * @returns {{x: number, y: number}} 分離のための力ベクトル
     */
    separation(allFish) {
        let steerX = 0;
        let steerY = 0;
        let count = 0;

        for (let other of allFish) {
            if (other === this) continue; // 自分自身は除外

            const distance = this.distanceTo(other);

            // 一定距離内の魚から離れる
            if (distance > 0 && distance < this.separationRadius) {
                // 離れる方向のベクトル
                const diffX = this.x - other.x;
                const diffY = this.y - other.y;

                steerX += diffX / (distance * distance); // 距離に反比例するように調整
                steerY += diffY / (distance * distance);
                count++;
            }
        }

        // 平均を取る
        if (count > 0) {
            steerX /= count;
            steerY /= count;
        }

        return { x: steerX, y: steerY };
    }

整列（Alignment）

周囲の魚の平均速度と同じ方向に力を受ける。

🐠「みんながこの向きに泳いでいるから自分も同じ向きに進もう。」
右へ倣え。

「周囲の魚の平均速度」を整列ベクトル$\boldsymbol{F}_{ali}$とする。つまり以下を整列ベクトルとする。

\boldsymbol{F}_{ali} = \frac{1}{n} \sum_{範囲内} \boldsymbol{v}

実装は以下。

    /**
     * Alignment (整列): 近くの魚と速度を合わせる
     * @param {Fish[]} allFish - すべての魚の配列
     * @returns {{x: number, y: number}} 整列のための力ベクトル
     */
    alignment(allFish) {
        let avgVx = 0;
        let avgVy = 0;
        let count = 0;

        for (let other of allFish) {
            if (other === this) continue;

            const distance = this.distanceTo(other);

            // 一定距離内の魚の速度を平均する
            if (distance > 0 && distance < this.alignmentRadius) {
                avgVx += other.vx;
                avgVy += other.vy;
                count++;
            }
        }

        if (count > 0) {
            avgVx /= count;
            avgVy /= count;

            // 平均速度に向かう力(現在の速度との差分)
            return {
                x: avgVx - this.vx,
                y: avgVy - this.vy
            };
        }

        return { x: 0, y: 0 };
    }

3つの力を受けた魚の挙動

上述の通り、先の３つの力（≒加速度）の影響を受けて、次の時刻の魚の速度ベクトルを以下の要領で計算する。
ここで、 $W_{coh}$, $W_{sep}$, $W_{ali}$はそれぞれ、結合、分離、整列の力が魚の速度ベクトルに影響を与える度合い(重み)である。

\begin{eqnarray}
\boldsymbol{v}(t + dt) &=& \boldsymbol{v}(t) + \frac{\boldsymbol{F}_{net}}{m}dt \\
&\simeq&  \boldsymbol{v}(t) + (W_{coh}\boldsymbol{F}_{coh} + W_{sep}\boldsymbol{F}_{sep} + W_{ali}\boldsymbol{F}_{ali}) dt
\end{eqnarray}

    /**
     * 次のフレームでの座標と速度を計算する
     * @param {number} deltaTime - 経過時間(秒)
     * @param {number} canvasWidth - キャンバスの幅
     * @param {number} canvasHeight - キャンバスの高さ
     * @param {Fish[]} allFish - すべての魚の配列(群体行動用)
     */
    update(deltaTime, canvasWidth, canvasHeight, allFish) {
        // Boidsアルゴリズムの3つの力を計算
        const coh = this.cohesion(allFish);
        const sep = this.separation(allFish);
        const ali = this.alignment(allFish);

        // 各力に重みを適用して速度に加算
        this.vx += coh.x * this.cohesionWeight;
        this.vy += coh.y * this.cohesionWeight;
        
        this.vx += sep.x * this.separationWeight;
        this.vy += sep.y * this.separationWeight;

        this.vx += ali.x * this.alignmentWeight;
        this.vy += ali.y * this.alignmentWeight;

        // 基本的な移動: 速度を座標に加算
        this.x += this.vx * deltaTime;
        this.y += this.vy * deltaTime;

        // 画面端の処理: 反対側から出現(トーラス構造)
        if (this.x < 0) this.x = canvasWidth;
        if (this.x > canvasWidth) this.x = 0;
        if (this.y < 0) this.y = canvasHeight;
        if (this.y > canvasHeight) this.y = 0;
    }

ここまでのコードをfishクラスとして実装し、そのほか、画面に描画するためのコードを記述。
コードの全量は以下を参照。

osakana-simulator/
├── index.html      # メインHTMLファイル（UI・レイアウト）
├── simulator.js    # シミュレーター本体クラス（初期化・更新・描画ループ）
├── fish.js         # 魚クラス（Boidsアルゴリズムの実装）
└── README.md       # このファイル

動作確認

冒頭の再掲になるが、以下のように魚群を模した挙動が再現できた。
見ていて楽しい！

発展：障害物

障害物をよける動作を追加する。

障害物クラスobstacle.jsを定義したうえで、以下のように第４の力：回避ベクトル $\boldsymbol{F}_{avo}$ を定義する。

\boldsymbol{F}_{avo} = \frac{1}{n} \sum_{範囲内} \frac{\boldsymbol{r_0}-\boldsymbol{r_c}}{ | \boldsymbol{r_0}-\boldsymbol{r_c} | } \frac{r_{avo} - (|\boldsymbol{r_0}-\boldsymbol{r_c}|-r_a)}{r_{avo}}

ここで、 $\boldsymbol{r_0}$ が魚の位置、 $\boldsymbol{r_c}$ が障害物の中心、 $r_{avo}$ が魚の回避半径、 $r_{a}$ が障害物の半径である。つまり、図の緑の部分の重なりが大きいほど強く回避する方向に力がかかる。

実装は以下。

    /**
     * Avoidance (回避): 障害物から離れる
     * @param {Obstacle[]} obstacles - すべての障害物の配列
     * @returns {{x: number, y: number}} 回避のための力ベクトル
     */
    avoidObstacles(obstacles) {
        let steerX = 0;
        let steerY = 0;
        let count = 0;

        for (let obstacle of obstacles) {
            // 障害物との距離を計算
            const distance = obstacle.distanceToPoint(this.x, this.y);

            // 一定距離内の障害物から離れる
            if (distance < this.avoidanceRadius) {
                // 障害物の中心から魚への方向ベクトルを取得
                const direction = obstacle.getDirectionFromCenter(this.x, this.y);

                // 距離に反比例する力（近いほど強く離れる）
                const force = (this.avoidanceRadius - distance) / this.avoidanceRadius;

                steerX += direction.x * force;
                steerY += direction.y * force;
                count++;
            }
        }

        // 平均を取る
        if (count > 0) {
            steerX /= count;
            steerY /= count;
        }

        return { x: steerX, y: steerY };
    }

コードの全量は以下。

osakana-simulator/
├── index.html      # メインHTMLファイル（UI・レイアウト）
├── simulator.js    # シミュレーター本体クラス（初期化・更新・描画ループ）
├── fish.js         # 魚クラス（Boidsアルゴリズムの実装）★
├── obstacle.js     # 障害物クラス（障害物の表現と距離計算）★
└── README.md       # このファイル

動作結果は以下。いい感じに障害物をよけて群れが動いてくれている。楽しい！

おわりに

さも自分が書いた感じですが、実装も、図も、全部claude codeにおまかせです・・・(claudeを初導入して威力を実感したかったこともあり）。やりたいことをREADME.mdに書く→「これを実現したいのですが、どのような技術スタックで実装するのがよいか提案してください」→「じゃあそれで」のムーブが強すぎます。

さすがに記事まで書かせると人間様のやることがなくなってしまうので、この記事の文章だけ自分で書いています。

もともとは、数年前に「21_21 DESIGN SIGHT」という美術館で「群れのルール」というインスタレーションの展示を見て、自分でも実装してみたい！と思ったのがきっかけだったのですが、画面を描画するとっかかりの部分で詰まってそのまま忘れ去っていたところ、近年のAIの台頭でこの部分のハードルが低くなったので改めて試してみたくなった、という経緯でした。手元で魚が泳いで大変満足です。

最後に、claude様の素晴らしいパフォーマンスぶりを貼って終わりにしようと思います。
もう人間いらないな・・・

↓コード修正はお手ものの

↓READMEも書いてくれる

↓git操作もできる

↓図も作れる (→svgならこのままパワポに貼って人間で微修正もできる)