2.7.5. Scipyでの実践的な最適化のためのガイド
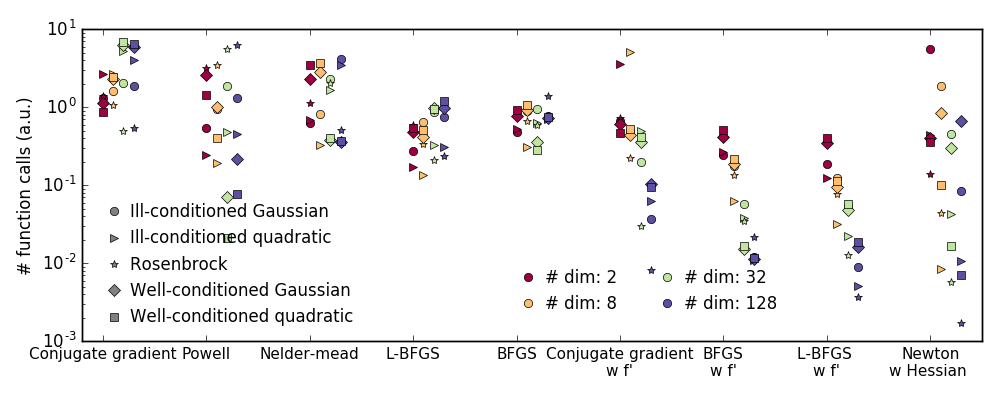
2.7.5.1. 手法の選択
すべての手法はscipy.optimize.minimize()のmethod引数として利用できます。
勾配が未知の場合:
- 一般的には、数値的に勾配を近似する必要がある場合でも、BFGSやL-BFGS が好ましいです。
これらはどちらもmethod引数を省略した場合のデフォルトで、問題に拘束条件や境界があるかによって選ばれます。 - 良条件下ではPowellやNelder-Meadの両者は勾配を必要とせず高次元でもうまく動きますが悪条件の問題ではこれらは挫折します。
勾配が既知の場合:
- BFGSまたはL-BFGS。
- BFGSの計算オーバーヘッドはL-BFGSより大きく、L-BFGSは共役勾配法よりも大きくなります。一方で BFGSはたいていの場合でCGと比べて少ない関数評価で済みます。なので共役勾配法は関数の計算コストが低い場合にはBFGSよりよい方法といえます。
ヘッセ行列がある場合:
- ヘッセ行列を計算できるなら、ニュートン法(Newton-CGまたはTCG)が好ましいです。
ノイズのある測定値の場合:
- Nelder-MeadまたはPowellを使います。
2.7.5.2. 最適化を高速化する
- 正しい手法を選択して(上記参照)、可能なら勾配やヘッセ行列を解析的に計算します。
- 可能なら前処理を利用します。
- 初期値を賢く選択します。例えば、多くの似たような最適化をするなら、別の結果でウォームアップした点から始めます。
- 精度が必要なければ
tol引数を使って許容誤差を緩めます。
2.7.5.3. 勾配の計算
勾配の計算、さらにはヘッセ行列の計算は、うんざりする作業ですが苦労する分の価値があります。Sympyによる記号計算は役に立つかもしれません。
非常によくある最適化が収束しない原因は、勾配の計算でのヒューマンエラーです。scipy.optimize.check_grad()を利用して勾配が正しいかを確認できます。この関数は与えた勾配と数値的に計算した勾配の差のノルムを返します:
>>> optimize.check_grad(f, jacobian, [2, -1])
2.384185791015625e-07
間違いを見つけるためにscipy.optimize.approx_fprime()も参照してください。
2.7.5.4. 総合演習
演習問題: 単純(?)な二次関数
np.random.seed(0)
K = np.random.normal(size=(100, 100))
def f(x):
return np.sum((np.dot(K, x - 1))**2) + np.sum(x**2)**2
時間計測してみましょう。最も高速な方法は?BFGSはどうしてうまく動作しないのでしょうか?
ソースコード
2.7.4.10. Alternating optimization — Scipy lecture notes
演習問題: 局所的に平らな最小値
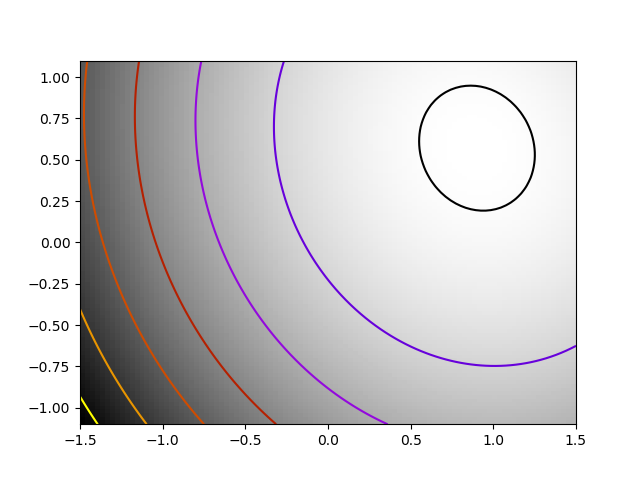
関数exp(-1/(.1*x**2 + y**2)を考えます。この関数は (0, 0) で最小になります。(1, 1) の初期値から始めて、この最小値から 1e-8 以内になるまで試しましょう。
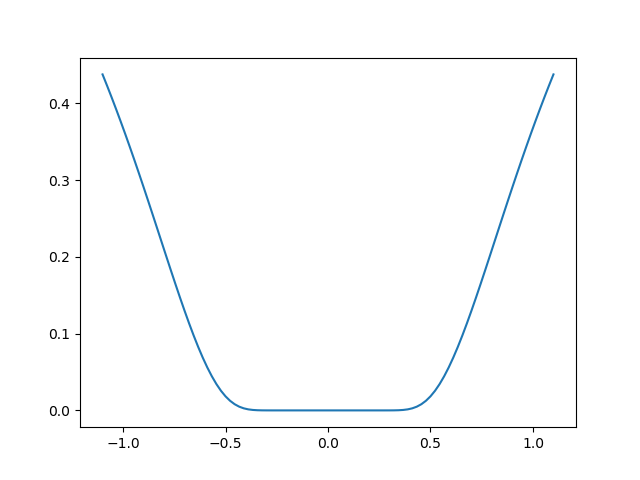
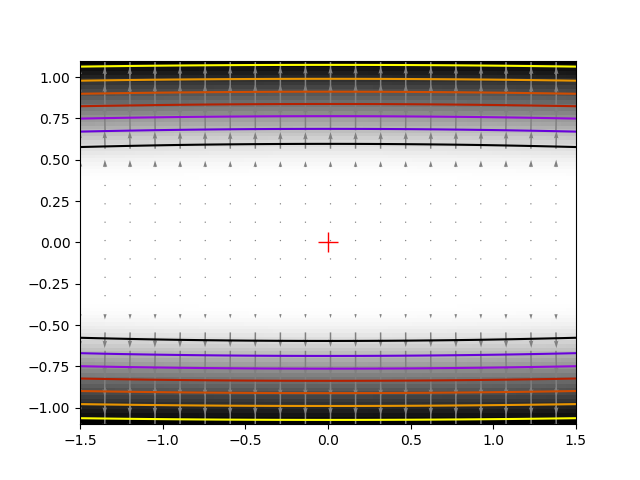
ソースコード
2.7.4.5. Finding a minimum in a flat neighborhood — Scipy lecture notes
関連リンク
元記事
2.7.5. Practical guide to optimization with scipy — Scipy lecture notes