趣味で宇宙開発を行う団体「リーマンサット・プロジェクト」がお送りする新春アドベントカレンダーです.まとめ記事はこちらからご覧になれます.
who are you?
アームを展開しての自撮りミッションを目指す10cm立方の超小型人工衛星rsp-01開発チームで,姿勢制御系を務めています.普段は,大学でロケットエンジンの数値計算をしています.
はじめに
ISSの軌道や衛星の姿勢を扱う記事が飛び出しましたので,この記事では,さらに遠くの太陽系惑星の運動を表示するところを目指してみたいと思います.
以下が軌道要素をもとに計算した軌道のプロットです.内側から水星,金星,...,海王星を表示しています.図の単位は,太陽と地球の平均距離である1天文単位です.
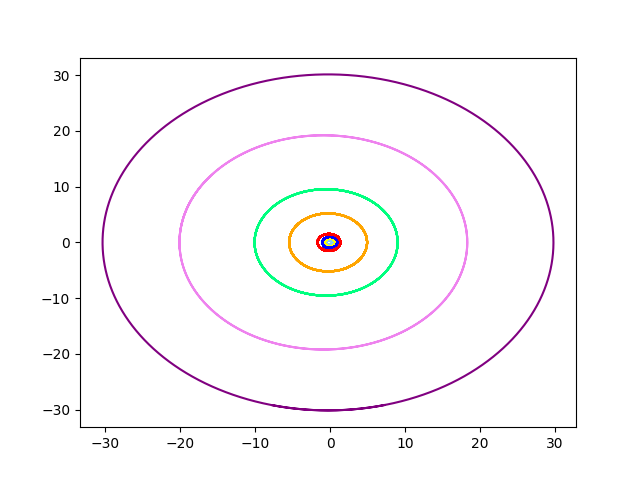
惑星の軌道
1.軌道決定に必要な変数の定義
惑星軌道は楕円形状として決定でき,半長径$a$と離心率$e$が必要です.
2つのパラメータは,2000年1月1日正午を基準とするユリウス世紀$T_{TDB}$を引数として,決定できます.係数は,「ミッション解析と軌道設計の基礎」を参照し付録のelements.pyのように作成しています.
\begin{align}
\sum_{k=1}^4 c_{p,k}{T_{TDB}}^{k-1}
\end{align}
2.ニュートンラプソン法による近点離角の導出
各時刻における衛星の位置を示す平均近点離角$M$も上式により決定されます.惑星の座標を決定するために必要な近点離角$E$をこれまでに得た離心率$e$と平均近点離角$M$を用いて求めます.このときに利用するのが,ケプラー方程式です.
\begin{align}
M=E-e\mathrm{sin}E
\end{align}
この式は,解析解が存在しないので,数値解を用います.ここで,$f(E)$を定義すると
\begin{align}
f(E)&=M-E+e\mathrm{sin}E\\
f'(E)&=e\mathrm{cos}E-1
\end{align}
であり,
\begin{align}
E'&=E-f(E)/f'(E)\\
\end{align}
座標の更新を繰り返すと,下図のように方程式の解に近づきます.$E$の値の変化が十分に小さくなった時点で,反復計算を打ち切ります.
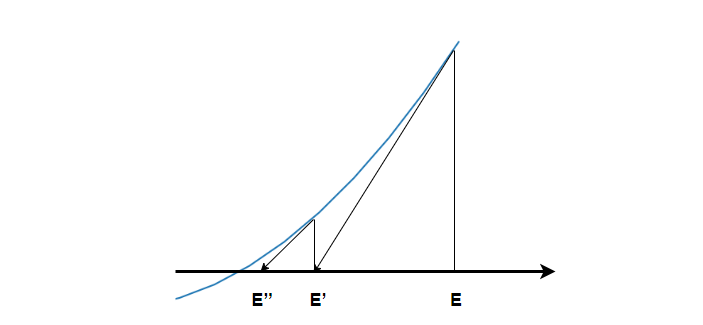
3.x,y座標系への変換
図のように距離を定義すると,惑星の$x$座標と$y$座標は,楕円の性質を利用して次式のように定義されます.
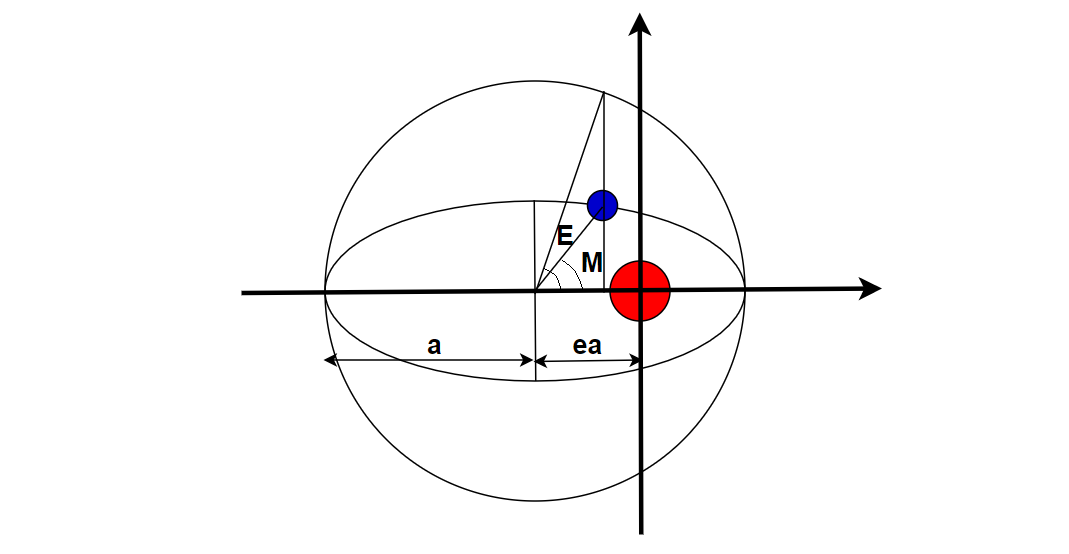
\begin{align}
x&=a\mathrm{cos}E-ae\\
y&=a\sqrt{1-e^2}\mathrm{sin}E
\end{align}
1.および2.で求めた$a$,$e$,$E$を代入することで,あるユリウス世紀$T_{TDB}$における惑星の位置$x$,$y$が求められました.
1.~3.の計算を繰り返し実行することで,惑星の運動を追うことができます.
本記事は,リーマンサット・プロジェクトアドベントカレンダー内で作成しました.
リーマンサット・プロジェクトは「普通の人が集まって宇宙開発しよう」を合言葉に活動をしている民間団体です.
他では経験できない「宇宙開発プロジェクト」に誰もが携わることができます.
興味を持たれた方は https://www.rymansat.com/join からお気軽にどうぞ.
@kentaniさんの「みんなで人工衛星、1人で家のテレビを遠隔操作」もオススメです.
付録
import numpy as np
def elems(num, JC):
coeff = np.empty((6, 4))
JC_term = np.array([[1.], [JC], [JC ** 2], [JC ** 3]])
if num == 1: #mercury
coeff = np.array([[0.38709831, 0, 0, 0], # semimajor axis: a
[0.20563175, 0.000020406 , -0.0000000284, 0.000000017], # eccentricity: e
[7.00498600, -0.00595160 , 0.00000081000, 0.000000041], # orbital inclination: i (for 3D)
[48.3308930, -0.12542290 , -0.0000883300, -0.000000196], # longitude of the ascending node: Omega ( for 3D)
[77.4561190, 0.158864300 , -0.0000134300, 0.000000039], # Perihelion longitude: ~omega
[252.250906, 149472.6746358, -0.0000053500, 0.000000002]]) # mean latitude: lamda
elif num == 2: #venus
coeff = np.array([[0.72332982, 0, 0, 0],
[0.00677188, -0.000047766, 0.0000000975, 0.000000044],
[3.39466200, -0.000856800, -0.00003244, 0.000000010],
[76.6799200, -0.278008000, -0.00014256, -0.000000198],
[131.563707, 0.004864600 , -0.00138232, -0.000005332],
[181.979801, 58517.815676, 0.000001650, -0.000000002]])
elif num == 3: #earth
coeff = np.array([[1.000001018, 0, 0, 0],
[0.01670862, -0.0000420370, -0.0000001236, 0.00000000004],
[0.00000000, 0.01305460000, -0.0000093100, -0.0000000340],
[0.00000000, 0.00000000000, 0.0000000000, 0.00000000000],
[102.937348, 0.32255570000, 0.0001502600, 0.00000047800],
[100.466449, 35999.3728519, -0.0000056800, 0.00000000000]])
elif num == 4: #mars
coeff = np.array([[1.523679342, 0, 0, 0],
[0.093400620, 0.00009048300, -0.0000000806, -0.00000000035],
[1.849726000, -0.0081479000, -0.0000225500, -0.00000002700],
[49.55809300, -0.2949846000, -0.0006399300, -0.00000214300],
[336.0602340, 0.44388980000, -0.0001732100, 0.000000300000],
[355.4332750, 19140.2993313, 0.00000261000, -0.00000000300]])
elif num == 5: #jupiter
coeff = np.array([[5.202603191, 0.0000001913, 0, 0],
[0.048494850, 0.0001632440, -0.0000004719, -0.000000002],
[1.303270000, -0.001987200, 0.0000331800 , 0.0000000920],
[100.4644410, 0.1766828000, 0.0009038700 , -0.000007032],
[14.33130900, 0.2155525000, 0.0007225200 , -0.000004590],
[34.35148400, 3034.9056746, -0.0000850100, 0.000000004]])
elif num == 6: #saturn
coeff = np.array([[9.554909596, -0.0000021389, 0, 0],
[0.055086200, -0.0003468180, 0.0000006456, 0.0000000034],
[2.488878000, 0.00255150000, -0.000049030, 0.0000000180],
[113.6655240, -0.2566649000, -0.000183450, 0.0000003570],
[93.05678700, 0.56654960000, 0.0005280900, 0.0000048820],
[50.07747100, 1222.11379430, -0.000085010, 0.0000000040]])
elif num == 7: #uranus
coeff = np.array([[19.218446062, -0.0000000372, 0.00000000098, 0],
[0.04629590, -0.000027337, 0.0000000790, 0.00000000025],
[0.77319600, -0.001686900, 0.0000034900, 0.00000001600],
[74.0059470, 0.0741461000, 0.0004054000, 0.00000010400],
[173.005159, 0.0893206000, -0.000094700, 0.00000041430],
[314.055005, 428.46699830, -0.000004860, 0.00000000600]])
elif num == 8: #neptune
coeff = np.array([[30.110386869, -0.0000001663, 0.00000000069, 0],
[0.0089880900, 0.00000640800, -0.0000000008, 0],
[1.7699520000, 0.00022570000, 0.00000023000, 0.0000000000],
[131.78405700, -0.0061651000, -0.0000021900, -0.000000078],
[48.123691000, 0.02915870000, 0.00007051000, 0.0000000000],
[304.34866500, 218.486200200, 0.00000059000, -0.000000002]])
temp = np.dot(coeff, JC_term)
elements = np.empty((3, 1))
elements[0] = temp[0]
elements[1] = temp[1]
elements[2] = temp[5] - temp[4] # M = lamda - ~omega
elements[2] = np.deg2rad(elements[2])
return elements
import matplotlib.pyplot as plt
def plot_2D(state_x, state_y):
fig = plt.figure()
plt.plot(state_x[0, :], state_y[0, :], color = 'skyblue')
plt.plot(state_x[1, :], state_y[1, :], color = 'yellow')
plt.plot(state_x[2, :], state_y[2, :], color = 'blue')
plt.plot(state_x[3, :], state_y[3, :], color = 'red')
plt.plot(state_x[4, :], state_y[4, :], color = 'orange')
plt.plot(state_x[5, :], state_y[5, :], color = 'springgreen')
plt.plot(state_x[6, :], state_y[6, :], color = 'violet')
plt.plot(state_x[7, :], state_y[7, :], color = 'purple')
plt.show()
import numpy as np
import elements as elems
import plotResult as pltResult
def newtonRaphson(e, meanE):
E = 2 * meanE
eps = 1e-10
while True:
E -= (meanE - E + e * np.sin(E)) / (e * np.cos(E) - 1)
if abs(meanE - E + e * np.sin(E)) < eps:
return E
def main():
JDbase = 2451545 # Julian century := 0 -> Julian day := 2451545
JY2JD = 36525 # Julian year = 0 -> Julian Day = 36525
dJD = 1
totalJD = 65000
JD = np.arange(JDbase, JDbase + totalJD, dJD)
imax = len(JD)
planet = 8
dimension = 2
state_x = np.empty((planet, imax))
state_y = np.empty((planet, imax))
temp_elem = np.empty(3, ) # a, e, M
r = np.zeros((dimension, 1))
for i in range(0, imax):
JC = (JD[i] - JDbase) / JY2JD
for planum in range(1, planet + 1):
temp_elem = elems.elems(planum, JC)
E = newtonRaphson(temp_elem[1], temp_elem[2])
state_x[planum - 1][i] = temp_elem[0][0] * (np.cos(E) - temp_elem[1][0]) #x
state_y[planum - 1][i] = temp_elem[0][0] * np.sqrt(1 - temp_elem[1][0] ** 2) * np.sin(E) #y
pltResult.plot_2D(state_x, state_y)
if __name__ == '__main__':
main()