点群の深層学習の世界をのぞいていくシリーズ
はじめに
iphoneにもLiDARカメラが搭載される昨今ですが、
ノイズや外れ値から無縁の精度を得るには未だ時間がかかりそうです。
「深層学習ならノイズ・外れ値に対してもっと頑強になれるんじゃね?」という期待の元、
深層学習系の点群の位置合わせ等について勉強していきます。
勉強の過程をそのまま書いてるので、
本番に行く前に前提知識の説明が膨大に膨れたりしますがご容赦ください
勉強の方針
https://arxiv.org/abs/2003.03164
https://github.com/XuyangBai/D3Feat.pytorch
D3Feat。学習ベースの特徴量検出と特徴量記述の抽出による位置合わせについて勉強します。
前提知識
特徴点(feature)と記述子(descriptor)
特徴点は特徴的な部分をポイントで抽出したもの、
記述子は特徴点周りの「領域」から周囲の情報を記述するもの。
https://graziegrazie.hatenablog.com/entry/2019/03/16/084321
KPConv
まだ論文は読んでない
D2-Net
まだ論文は読んでない
距離学習 metric learning
https://qiita.com/jw-automation/items/7bbe1c872fcec7fa6c1d
https://qiita.com/gesogeso/items/547079f967d9bbf9aca8
畳み込みネットワークで分類しようとすると、特徴が違いすぎて同じ分類にできなかったり、
逆に違うものと見なしたいのに特徴が似すぎていて同じものとみなされてしまうようなものがあったとする。
このような問題に対して「ペナルティ」を導入する。
同じ分類になるならそのデータ同士が近くなるようにペナルティを設定し、
違う分類なら絶対に同じにならないように遠いペナルティを設定する。
・・・・というようなイメージらしい。
本稿がそれをどのように実装するかはこれを書いてる時点ではわかってない。
→追記。
https://www.softbanktech.co.jp/special/blog/cloud_blog/2019/0068/
「ペナルティ」を損失関数で設計します。
方法はいくつかあるようですが、本稿では「Triplet Loss」を採用しているようなので、
これについて勉強します。
TripletLoss = \max(0, (d_{pos}-d_{anc}) - (d_{neg}-d_{anc}) + \alpha)
まず、三枚の画像を考えます。
これをAグループに属するものとそうでないものをわけます。
$d_i$はCNNで出力された特徴です。$d_{anc}$はAグループの「基準」となる画像の特徴、
$d_{pos}$はグループAに属するであろう画像の特徴、$d_{neg}$はグループAには決して属さない画像の特徴です。
ネガティブな場合
式の意味について考えます。
maxの中の値がマイナスであれば、損失は0として出力されます。
ネットワークでいえば、これ以上最適化が必要ない理想的な状態です。
損失が0になる理想的な状態となる状態は、$(d_{neg}-d_{anc})$がとてもとても大きい場合です。
違う分類なら絶対に同じにならないように遠いペナルティを設定する。
$(d_{neg}-d_{anc})$は、異なるグループ同士がどれくらい距離が離れているかを計算したもの。
Aグループとの距離が最初からすでに十分離れているのであれば、ペナルティを課す必要はないので
損失は0、すなわち最適化を行う必要はありません。
ポジティブな場合
同じ分類になるならそのデータ同士が近くなるようにペナルティを設定する
$(d_{pos}-d_{anc})$がとてもとても大きい場合というのは、
同じグループなのに距離が大きくなってしまっている状態なので、
より近くなるようにパラメータを調整しなければなりません。
なので計算結果としては、$(d_{pos}-d_{anc})$の大きな値を出力し、
最適化のフェーズで$\alpha$を調整することで、ペナルティを設定します。
L2ノルム
\| {\bf x} \|_ = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2 }
読む(論文)
0
3D分野では特徴記述子がぜんぜん研究進んでないからもっと研究してこうぜ!という目的。
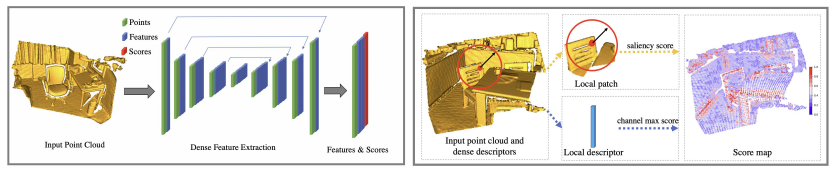
3D点群ごとに密度や構造が変造する問題に対して、畳み込みネットワークを活用することで
特徴量記述子の検出および、特徴点のスコアを予想します。
1
最近の研究でも学習による特徴量記述子に関する研究が進んでいますが、
学習ベースのキーポイント検出はあまり盛んではありません。
キーポイントの検出と記述子を合わせて学習しないと結果が一致しない場合があるので、
どちらも両方を学習するフレームワークを目指します。
この論文の重要なポイントは3つです。
(1)共有学習:D2-Netの拡張・KPConvによる畳み込み演算により、
特徴検出・記述子を密に結合させて学習を行います。
(2)密度に対する不変性:D2-Netを順応させることで点群固有の密度の違いに対する問題に対応します。
(3)収束性:収束されない場合があるので、トレーニング中に計算される特徴マッチングの結果より、
収束されるように新たな自己監視検出器損失を提案します。
3
この論文は、キーポイントの検出と記述子を合わせた学習はD2-netに触発されています。
D2-netは2D画像をベースにしているので点群用にカスタマイズする必要があります。
以降では、まばらでいて不規則に登録される点群に対して、
特徴点・記述子を抽出する基本的な流れと、本稿における「肝」を説明します。
3.1 「密」な特徴量記述子の抽出
過去の研究で、不規則な点群に対して適切に特徴をキャプチャする方法として
KPConvという方法が提案されました。まず簡単にKPConvを確認します。
ある点xでの「密な」特徴$F_in$をカーネル$g$で畳み込み式は下記で表されます。
(F_in * g) = \sum_{x_{i}\in N_x}g(x_i-x)f_i
$x$を中心としたカーネルサイズ$N_x$の範囲内にあるポイントに対して、
周囲のポイントの差分とその特徴$f_i$を掛け合わせます。
(おそらくこの時点で既に各ポイントの特徴$f_i$は計算済みである。)
$g$については下記式。
g(x_i-x)=\sum_{K}^{k=1}h(x-x_i,x_k)W_k
$h$は相関関数、$x_k$はカーネルポイント・・・・カーネルポイントってなに?
詳細はKPConvの論文を読まないとわからなそうです。
(※これを読んでいる時点としては、ソースを解析しながら調べることにします。)
この時点では、密度に対する不変性は確保できていません。
よって、ここでは正規化を行う式を採用します。
g(x_i-x)=\frac{1}{|N_x|}\sum_{K}^{k=1}h(x-x_i,x_k)W_k
このネットワークにより出力されるのは、$F \in R^{N×c}$の密な特徴行列です。
この$F_i$が$c$次元の「特徴量記述子$d_i$」となります。
d_i = F_{i:},d_i\in R^c
$N×c$の直積集合なので、1つのポイントあたりc次元の特徴が存在する。
3.2 「密」な特徴点の抽出
概要
D2-netでは、2D画像に対する特徴点の抽出のアプローチとして、
隣接するピクセルを近傍として選択することで計算を行います。
これを3Dに置き換えるには、あるポイントの「半径近傍」に置き換えることで対応します。
しかし、それだけだとD2-netの性質上、局所的にポイント数が少ない領域は
誤った高スコアになってしまい、正しい計算が行えません。
したがって、密度に対して不変性を保ってスコアを計算しなければなりません。
問題を定式化するために、数式で整理します。
記述子の項で$F \in R^{N×c}$を定義しました。
これに対して、$D_k(k=1,\cdots,c)$を定義します。
D^k = F_{:k},D^k\in R^N
あるポイントに対して抽出されたc個の密な記述子を、$D^k$と表記します。
本稿では、あるポイント$x_i$がキーポイントであるかを以下の基準で判断します。
(x_iはキーポイントである)\\
⇔\\
(1) k = \underset{t}{\textrm{argmax}}(D_{i}^{t})\\
(2) i = \underset{j\in N_{x_{i}}}{\textrm{argmax}}(D_{j}^{t})\\
まず$F$は$N×c$の直積からなる集合であるので、カラムは$1,\cdots,c$です。
そのうち、$x_i$に対応する$D_i$は、i番目の行になります。
よって、上記の内容としては、
(1)$D_i$の中で最大の特徴をもつのは何列目の特徴であるかを取得し、それを[k]と置いた後、、
(2)$x_i$の周囲のポイントの$D$を比較し、これらの$D$のなかでk列目の値が最大なのが$x_i$であることを確認する
これが基準の概要となります。
詳細
顕著性スコア:密度不変性を考慮した計算
ここでは、あるポイントが他のポイントと比べてどれだけ顕著か、どれだけ特徴的かをスコアで定義します。
D2-Netの定義のままだと、密度の不変性が保てないので、下記式を定義します。
\alpha_{i}^{k} = \frac{exp(D_{i}^{k})}{\sum_{x_j \in N_{x_{i}}} exp(D_{j}^{k})}\\
⇒convert for 3D⇒\\
\alpha_{i}^{k} = ln(1 + exp(D_{i}^{k} - \frac{1}{|N_{x_{i}}|}\sum_{x_j \in N_{x_i}} D_j^k))
その特徴$D_i^k$と周辺の特徴の平均値$\frac{1}{|N_{x_{i}}|}\sum_{x_j \in N_{x_i}} D_j^k$の差分から計算されます。
また、合計の代わりに平均応答を使うやり方もあるらしい(が、どこにその式が記載されてるかよくわからない)
チャネルの最大スコア
\beta_{i}^{k} = \frac{D_i^k}{max_t (D_i^t)}
あるポイント$x_i$に対して、c個ある特徴のうち最大の値で各特徴の値を割っていきます。
このスコアは、最も優れた次元の特徴を取得するのに利用されるらしい。
最後
s_i = max_k(\alpha_i^k \beta_i^k)
そしてこの式でスコアを計算します。
もっともスコアが高いものを、キーポイントとして選択します。
4
記述子の損失
特徴点検出・記述子を密に結合させて学習させるには損失をどのように計算するか定義しなければなりません。
まず、現在手元にある情報を整理します。
あるポイント$x_i$に対して、記述子$d_i \in R^c$と、スコアが高いほど特徴点としてみなされる$s_i$が計算されています。
さて、点群A,Bの2つのうち、$A_i,B_i$というペアを考えます。
$A_i,B_i$が同じ箇所の周辺のポイントを指しているなら密な特徴の差分はほぼほぼ0になるはず。
これを式にすればL2ノルムで下記のようになります。
d_{pos}(i)=\| {\bf d_{A_{i}} - d_{B_{i}}} \|_{2}
同じ特徴になるであろう物同士の差分なので、これを「ポジティブ」な差分距離$d_{pos}$とみなします。
これに対して、同じ特徴にはならないだろうという者同士の「ネガティブ」な差分距離$d_{neg}$も計算します。
d_{neg}(i)=min(\| {\bf d_{A_{i}} - d_{B_{j}}} \|_{2})\\
such that \| {\bf B_j - B_i} \|_{2} > R
Rは「この距離の範囲内なら同じ特徴だろう」とみなせる距離です。
この距離よりも大きくなる$B_j$とは、数式的には$B_i$の特徴とはまず異なるだろうという特徴になります。
さらに$min(| {\bf d_{A_{i}} - d_{B_{j}}} |_2)$とすることで、
特徴はちがくとも全く違うというほどでもなく、ぎりぎり違うような特徴との差分を計算したものが、
上式の「ネガティブ」な差分距離の意味である、・・・と私は認識しています。
L_desc = \frac{1}{n}\sum_{i}(max(0,d_{pos}(i)-M_{pos}) + max(0,M_{neg}-d_{neg}(i)))
計算された損失について。
この学習のベースには、距離学習の考え方があります。
$(max(0,d_{pos}(i)-M_{pos})$の計算によって、
$x_{A_i}$と$x_{B_i}$の特徴同士の距離の差分$d_{pos}(i)$と、基準$M_pos$との差分が小さい場合は
同じポイントであるとみなす、というコンセプトのもとで損失計算・パラメータを調整し、
$max(0,M_{neg}-d_{neg}(i))$の計算によって、
異なるポイント同士である$x_{A_i}$と$x_{B_j}$の特徴の距離が、大きすぎる場合には
「距離学習 metric learning」的にはパラメータの調整が必要なく十分にカテゴリが離れている、
・・・・というコンセプトのもとで損失計算・パラメータを調整する。
要約するなら、
$(max(0,d_{pos}(i)-M_{pos})$はターゲットとなる2つのポイントが異なれば異なるほど大きくなり、
$max(0,M_{neg}-d_{neg}(i))$では、周囲のポイントとの特徴の距離と同じであればあるほど大きくなる。
$L_desc$は、大きくなる値が小さくなるように最適化を行うための損失関数。
すなわち、2つのポイント$A_i,B_i$が同じになるように、そして、周囲のポイントの特徴と
ターゲットのポイントの特徴大きく異なるように最適化を行うための損失関数。
・・・・と、私は認識します。
**$M_{pos},M_{neg}$**ってなんだろう?この節まで書いた時点ではわかってません。
https://arxiv.org/pdf/1705.10872.pdf
をちらっと読みましたが、読み方が浅いせいか明確にはわかりません。
「前提知識」の項の「距離学習 metric learning」的に言えば、
$d_{pos}$と同じグループに属するカテゴリの基準値が$M_{pos}$となります。
$d_{pos}$にはターゲットのポイント間の距離が入っているので、
$M_{pos}$には同じポイントとみなす閾値めいた数値が入っている・・・?
よくわかりません。
特徴点の損失
L_detect = \frac{1}{n}[(d_{pos}(i)-d_{neg}(i))(s_{A_i} + s_{B_i})]
$d_{pos} - d_{neg} < 0$なら、正しいマッチングが行えていることを示しており、
$L_detect$は$s_{A_i},s_{B_i}$が高くなるように促します。
$d_{pos} - d_{neg} > 0$なら、現在のネットワークでマッチングを行うのは不十分であることを示しており、
$L_detect$は$s_{A_i},s_{B_i}$が低くなるように促します。
一致する対応には高いスコア、一致しない対応には低いスコアを予測し、損失を最小限に抑えます。