全体像もまだ把握しきれていない著者が、メモ代わりに記載したものをまとめたものです。
Pytorchのチュートリアルの内容+αで調べた内容をまとめます。
(・・・と、書きましたがほとんどチュートリアルに準拠してません。)
自在に使えることを目標にして、わかるものを確定させてから、
コツコツと実装していく方針で勉強します。
今回は第2章です。
前 -> https://qiita.com/akaiteto/items/9ac0a84377600ed337a6
はじめに
前回、ニュートラルネットワークの各層の処理を見るだけに終わったので、
今回は最適化を中心に勉強します。
前提として、MNISTのサンプルソースをただ動かすだけなのは少しわかりにくいと感じたので、
できるだけシンプルな例を位置から組んで実際に動かしてから、
そこから自力で各種手法を自力で実装する事を目標に勉強します。
ついでに自作の最適化手法をニュートラルネットワークに組み込んでみます。
なお、実装するものはただの最急降下法です。
ニュートラルネットワークに自作の最適化手法を実装するときの参考になるかもしれません。
ネットワークの学習
前回の勘違い
前回、損失関数の説明で以下のような計算結果を提示しました。
やったこととしては至ってシンプルです。
まず適用な入力データを定義したネットワークに入力し、
出力値(特徴の情報が入ったデータ)を取得しました。
その後、その他いろんな入力データに対しても同様に行い、
最初に計算した出力地との「誤差」を計算し、それを「評価」として出力しました。
# 実行結果
*****学習フェーズ*****
ネットワーク学習用の入力データ
tensor([[[[0., 1., 0., 1.],
[0., 0., 0., 0.],
[0., 1., 0., 1.],
[0., 0., 0., 0.]]]])
*****評価フェーズ*****
同じデータを入力
input:
tensor([[[[0., 1., 0., 1.],
[0., 0., 0., 0.],
[0., 1., 0., 1.],
[0., 0., 0., 0.]]]])
評価 tensor(0., grad_fn=<MseLossBackward>)
ちょっと違うデータを入力
input:
tensor([[[[0., 2., 0., 2.],
[0., 0., 0., 0.],
[0., 2., 0., 2.],
[0., 0., 0., 0.]]]])
評価 tensor(0.4581, grad_fn=<MseLossBackward>)
ぜんぜん違うデータを入力
input:
tensor([[[[ 10., 122., 10., 122.],
[1000., 200., 1000., 200.],
[ 10., 122., 10., 122.],
[1000., 200., 1000., 200.]]]])
評価 tensor(58437.6680, grad_fn=<MseLossBackward>)
「きっとこの評価値を閾値で判定して同じものかどうか判断するんだろうなー」
と、当時の私は思いました。
0.5以上離れてたら違うデータとしてみなすのかな?くらいの認識です。
出力された値とは、いわば各データの特徴を抽出した数値。
だから、CNNというのはその特徴がどれくらい近いか見るための物なんだ!と。
・・・が、これはいろいろやることが足りていません。
今のままではただフィルターをかけただけです。学習というものを私は正しく理解していませんでした。
正解データA
tensor([[[[0., 2., 0., 2.],
[0., 0., 0., 0.],
[0., 2., 0., 2.],
[0., 0., 0., 0.]]]])
入力データB
tensor([[[[0., 1., 0., 1.],
[0., 0., 0., 0.],
[0., 1., 0., 1.],
[0., 0., 0., 0.]]]])
評価 tensor(0.4581, grad_fn=<MseLossBackward>)
学習フェーズにおける神髄、それは、
「微妙に違うけど実は同じものを指している入力データA、Bを、
同じものとして認識できるようにしようぜ!!」ということです。
評価 tensor(0.4581, grad_fn=<MseLossBackward>)
誤差として出力されたこの数値。
この数値は入力データAとBがどれくらいズレているか表すもの。
数値上では誤差が発生していますが、実はAとBは同じものなので、
誤差は理想的には「0」でなければならないのです。
すなわち、学習の本質とは
入力データAとBの大きい誤差、「0.4581」と出力されたものを
限りなく「0」で出力されるように「小手先を加える」こと、これこそが本質。
誤差を0として出力するようにネットワークの各層の「重み」を調整することで、
「誤差はないよーAとBは同じだよー」と”学習”させる事が本質なのです。
最適化してみる
最適化(思考停止)
重みの調整はどんな計算式で調整しているのかな?
・・・というのは一旦おいておいて、まずは思考停止でpytorchで学習させてみます。
わけもわからずいきなりMNISTの例でいろんなかっこいい層を使うのは嫌なので、
理解している範囲でよりシンプルな例でテストしてみます。
パターンA
tensor([[[[0., 1., 0., 1.],
[0., 1., 0., 1.],
[0., 1., 0., 1.],
[0., 1., 0., 1.]]]])
パターンB
tensor([[[[1., 1., 1., 1.],
[0., 1., 0., 1.],
[0., 1., 0., 1.],
[1., 1., 1., 1.]]]])
上記の2つのパターンを学習・テストさせてみましょう。
全体
import torch.nn as nn
import torch.nn.functional as F
import torch
from torch import optim
import matplotlib.pyplot as plt
import numpy as np
class DataType():
TypeA = "TypeA"
TypeA_idx = 0
TypeB = "TypeB"
TypeB_idx = 1
TypeOther_idx = 1
def outputData_TypeA(i):
npData = np.array([[0,i,0,i],
[0,i,0,i],
[0,i,0,i],
[0,i,0,i]])
tor_data = torch.from_numpy(np.array(npData).reshape(1, 1, 4, 4).astype(np.float32)).clone()
return tor_data
def outputData_TypeB(i):
npData = np.array([[i,i,i,i],
[0,i,0,i],
[0,i,0,i],
[i,i,i,i]])
tor_data = torch.from_numpy(np.array(npData).reshape(1, 1, 4, 4).astype(np.float32)).clone()
return tor_data
class Test_Conv(nn.Module):
kernel_filter = None
def __init__(self):
super(Test_Conv, self).__init__()
ksize = 4
self.conv = nn.Conv2d(
in_channels=1,
out_channels=4,
kernel_size=4,
bias=False)
def forward(self, x):
x = self.conv(x)
x = x.view(1,4)
return x
# テスト時データ準備
input_data = []
strData = "data"
strLabel = "type"
for i in range(20):
input_data.append({strData:outputData_TypeA(i),strLabel:DataType.TypeA})
for i in range(20):
input_data.append({strData:outputData_TypeB(i),strLabel:DataType.TypeB})
print("以下のパターンのテストデータを計200個準備")
print("パターンA")
print(outputData_TypeA(1))
print("パターンB")
print(outputData_TypeB(1))
print("この2つのパターンが識別できるか確かめます。")
print("\n\n")
# ネットワーク定義
Test_Conv = Test_Conv()
# 入力
import torch.optim as optim
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(Test_Conv.parameters(), lr=0.001, momentum=0.9)
print("***学習させる前にやってみる***")
##学習したモデルで適当なデータを入れてみる。
NG_data = outputData_TypeA(999999999)
answer_data = [DataType.TypeA_idx]
answer_data = torch.from_numpy(np.array(answer_data).reshape(1).astype(np.int64)).clone()
print("\n\n")
outputs = Test_Conv(NG_data)
_, predicted = torch.max(outputs.data, 1)
correct = (answer_data == predicted).sum().item()
print("正答率: {} %".format(correct / len(predicted) * 100.0))
print("***学習フェーズ***")
epochs = 2
for i in range(epochs):
for dicData in input_data:
# 学習用データの準備
train_data = dicData[strData]
# 正解用データの準備
answer_data = []
label = dicData[strLabel]
if label == DataType.TypeA:
answer_data = [DataType.TypeA_idx]
elif label == DataType.TypeB:
answer_data = [DataType.TypeB_idx]
else:
answer_data = [DataType.TypeOther_idx]
answer_data = torch.from_numpy(np.array(answer_data).reshape(1).astype(np.int64)).clone()
# 最適化処理
optimizer.zero_grad()
outputs = Test_Conv(train_data)
loss = criterion(outputs, answer_data)
# print(train_data.shape)
# print(outputs.shape)
# print(answer_data.shape)
#
# exit()
loss.backward()
optimizer.step()
print("\t", i, " : 誤差 = ",loss.item())
print("\n\n")
print("***テストフェーズ***")
##学習したモデルで適当なデータを入れてみる。
input_data = outputData_TypeA(999999999)
answer_data = [DataType.TypeA_idx]
answer_data = torch.from_numpy(np.array(answer_data).reshape(1).astype(np.int64)).clone()
outputs = Test_Conv(input_data)
_, predicted = torch.max(outputs.data, 1)
correct = (answer_data == predicted).sum().item()
print("正答率: {} %".format(correct / len(predicted) * 100.0))
exit()
以下のパターンのテストデータを計200個準備
パターンA
tensor([[[[0., 1., 0., 1.],
[0., 1., 0., 1.],
[0., 1., 0., 1.],
[0., 1., 0., 1.]]]])
パターンB
tensor([[[[1., 1., 1., 1.],
[0., 1., 0., 1.],
[0., 1., 0., 1.],
[1., 1., 1., 1.]]]])
この2つのパターンが識別できるか確かめます。
***学習させる前にやってみる***
正答率: 0.0 %
***学習フェーズ***
0 : 誤差 = 1.3862943649291992
0 : 誤差 = 1.893149733543396
0 : 誤差 = 2.4831488132476807
0 : 誤差 = 3.0793371200561523
0 : 誤差 = 3.550563335418701
0 : 誤差 = 3.7199602127075195
0 : 誤差 = 3.3844733238220215
0 : 誤差 = 2.374782085418701
0 : 誤差 = 0.8799697160720825
0 : 誤差 = 0.09877146035432816
0 : 誤差 = 0.006193255074322224
0 : 誤差 = 0.00034528967808000743
0 : 誤差 = 1.8000440832111053e-05
0 : 誤差 = 8.344646857949556e-07
0 : 誤差 = 0.0
0 : 誤差 = 0.0
0 : 誤差 = 0.0
0 : 誤差 = 0.0
0 : 誤差 = 0.0
0 : 誤差 = 0.0
0 : 誤差 = 0.0
0 : 誤差 = 0.0
0 : 誤差 = 0.0
.
.
.
***テストフェーズ***
正答率: 100.0 %
シンプルなソースですが一つずつ見てみます。
ネットワークの定義
class Test_Conv(nn.Module):
kernel_filter = None
def __init__(self):
super(Test_Conv, self).__init__()
ksize = 4
self.conv = nn.Conv2d(
in_channels=1,
out_channels=4,
kernel_size=4,
bias=False)
def forward(self, x):
x = self.conv(x)
x = x.view(1,4)
return x
MNISTでは入力データとして一度にすべてのデータを入れていました。
ですがそれだと規模が大きくなりすぎて直観的にわかりづらそうだったので、
1枚1枚モノクロの画像をいれていくように設定しています。
畳み込み層$out_channels=4$なので4つの特徴をフィルターで抽出し、
$x.view$では正解のラベルと比較するために次元を整えています。
学習させる前に適用してみる
print("***学習させる前にやってみる***")
##学習したモデルで適当なデータを入れてみる。
NG_data = outputData_TypeA(999999999)
answer_data = [DataType.TypeA_idx]
answer_data = torch.from_numpy(np.array(answer_data).reshape(1).astype(np.int64)).clone()
print("\n\n")
outputs = Test_Conv(NG_data)
_, predicted = torch.max(outputs.data, 1)
correct = (answer_data == predicted).sum().item()
print("正答率: {} %".format(correct / len(predicted) * 100.0))
学習させる前にやってみます。
コードは違いますが、「前回の勘違い」の再現です。案の定、正解率は0%です。
ネットワークの学習
# 学習用データの準備
train_data = dicData[strData]
# 正解用データの準備
answer_data = []
label = dicData[strLabel]
if label == DataType.TypeA:
answer_data = [DataType.TypeA_idx]
elif label == DataType.TypeB:
answer_data = [DataType.TypeB_idx]
else:
answer_data = [DataType.TypeOther_idx]
answer_data = torch.from_numpy(np.array(answer_data).reshape(1).astype(np.int64)).clone()
# 最適化処理
optimizer.zero_grad()
outputs = Test_Conv(train_data)
loss = criterion(outputs, answer_data)
loss.backward()
optimizer.step()
print("\t", i, " : 誤差 = ",loss.item())
「前回の勘違い」の項の中で、以下のように書きました
入力データAとBの大きい誤差、「0.4581」と出力されたものを
限りなく「0」で出力されるように「小手先を加える」こと、これこそが本質。
ネットワークの学習ではこの処理を行っています。
処理のはじめには、まず$train_data$にパターンA・パターンBのいずれかのデータを一つだけ入れます。
outputs = Test_Conv(train_data)
ネットワーク内部では4つのフィルターをかけることで4つの特徴を計算し、
「1つ」のデータあたり4つの特徴を内包したデータを出力します。
次元で言えば[1,4]のデータです。
続けて、正解データについても準備します。
answer_data = torch.from_numpy(np.array(answer_data).reshape(1).astype(np.int64)).clone()
出力された「1つのデータ」に対する正解を設定します。
文字列は設定できないので、パターンAのデータであれば「0」、
パターンBのBであれば「1」と設定します。
1つのデータに対する正解データなので、正解データの次元は[1]のデータです。
次元のイメージ図
# 今回の例
[出力データの構造]
- データ
- 1つ目の特徴
- 2つ目の特徴
- 3つ目の特徴
- 4つ目の特徴
[正解データの構造]
- データに対する回答(1?0?)
loss = criterion(outputs, answer_data)
そして誤差を計算します。
各正解ラベルごとに重みを調整するので、正解ラベルも一緒に入れます。
optimizer.step()
そして最適化、というこれまでにはまだ出てきていない新たな処理を実行します。
forループの中でタイプA、タイプBごとの出力データをポンポン入れていき、
各タイプ内での誤差が0に近づくように、重みを調整しているのだと思います。
(今は思考停止フェーズなので、どんな調整を行っているかは後々勉強します!)
最適化とは何か。
wikipediaまんまですが、プログラムの最適な状態をさがすことを最適化といいます。
ここでは、誤差が最小になるのはどこなのかを計算することで、最適化を行います。
実行結果
実行結果を見てみます。
***テストフェーズ***
正答率: 100.0 %
はい、100%になっていますね。
学習前は0%だったものが、無事学習できました。
最適化(自分で実装)
処理の肝は$optimizer.step()$で行われる最適化処理です。
pytorchで使える最適化の手法はたくさんあり、今回はSGD(確率的勾配降下法)というものを選びました。
ここまでおこなった最適化処理を振り返ると、
pytorchですでに実装された関数を使っているだけで、私はなにもやっていません。
論文で何かの最適化手法を実装したいと思ったとき、
具体的にはどうすればよいのでしょうか?
・・・ということで、
「最急降下法(GD)」というシンプルな最適化手法を例にまずは実装します。
先に言いますと、最急降下法は実用的ではないです。
今回使用したSGDから時代が逆行しています。ただ、勉強には向いている気がするので、
最急降下法を実装してみます。
最適化のイメージ
最適化ってなにやるの?というのを直観的なイメージをかためるために、簡単に式で表してみます。
(これを作った時点で私は論文も何も読んでません。
イメージなので厳密な意味で間違えてます。軽く参考にする程度で・・・)
y = f(x)
ネットワークに入力データを入れたら特徴の値が数値で帰ってきました。
言い換えるなら、入力データ$x$を入れたら出力として$y$が返ってきた状態です。
これを$y=f(x)$とします。
gosa = |f(A)-f(B)|
そしてこの式に対して、入力データ$A$と$B$を与えたとき、
差が最小値になるように調整したいわけです。
AとBは実は同じデータなので、同じ出力結果を得たいわけです。
gosa(weight) = |g(A)-g(B)|\\
g(x) = weight * f(x)
ここでパラメータ$weight$を導入します。
ネットワークの関数である$f(x)$に重みを与えてやります。
この式の導入により、誤差を最小にしたいという問題は、
誤差を最小にできるパラメータ$weight$を発見することに置き換わります。
$gosa(weight)$が最小となる$weight$を見つけさえすれば良いわけです。
簡単なグラフで最適化
簡単な式で最適化してみます。
最小化問題と言うと、中学生のころに$y=x^2$の問題をやりました。
当時は、手動の計算を前提として、非常に限定的な計算式で最小値を求めていましたね。
ここでは、$y=x^2$を$gosa(weight)$であると仮定して、
最急降下法という最適化手法で解いてみます。
y = x^2\\
\frac{d}{dy}
=
2x
$y=x^2$の微分$\frac{d}{dy}$は上記のようになります。
$y=x^2$と言うグラフは、$\frac{d}{dy}$という最小の単位で徐々に変化していくグラフとなります。
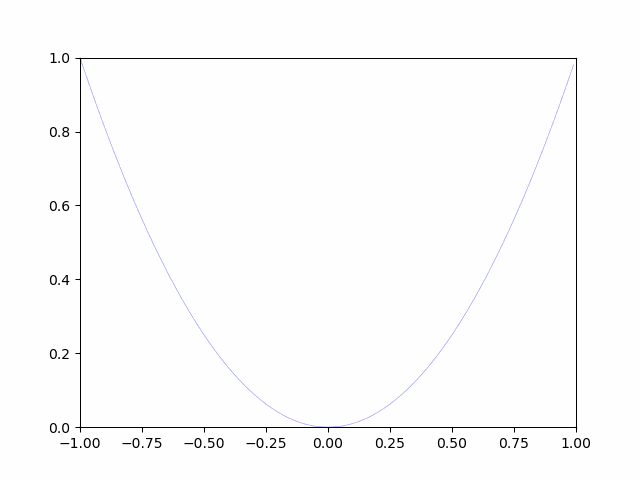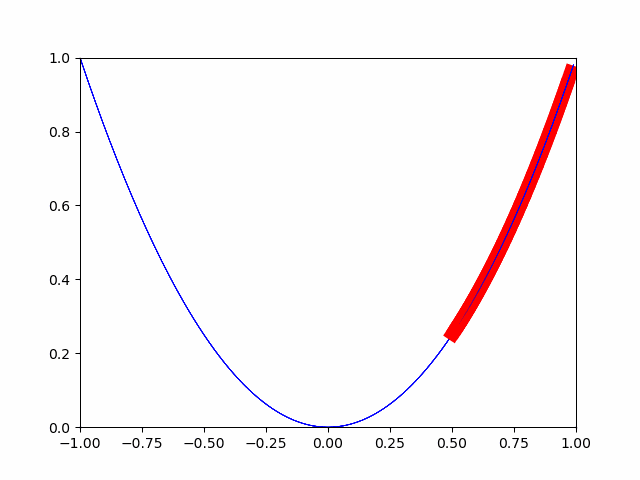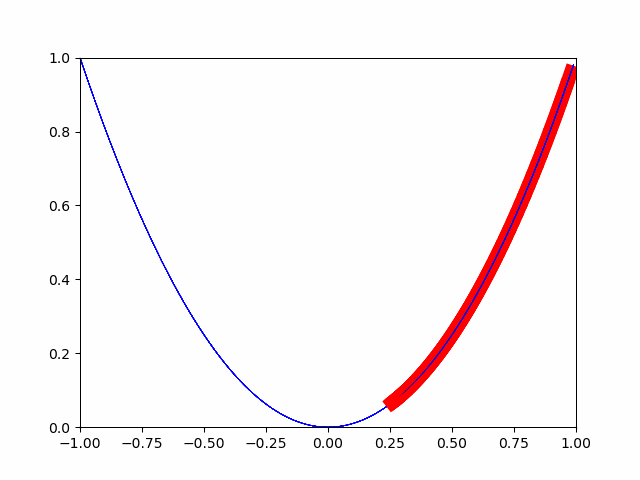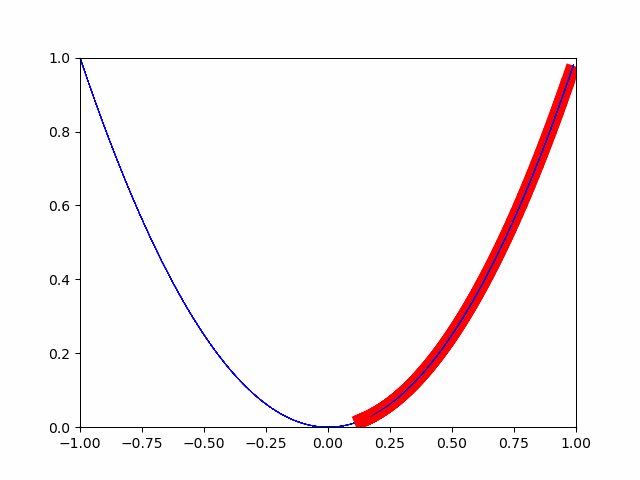
最急降下法とは、微小変化分だけ徐々に徐々に移動させて、
微小変化分が完全に0になった地点が最小値であるとみなす手法です。
(中学の頃、傾きが0になる地点は最小・最大になるみたいな問題がありましたね。)
ということで、pytorchの自動微分機能を使ってやってみます。
画像の通り、徐々に最小値に向かっていることがわかります。
このようにして、最小値に対する最適化が行われます。
以下、ソース。
if __name__ == '__main__':
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import numpy as np
import torch
import torchvision
import torchvision.transforms as transforms
def func(x):
return x[0] ** 2
fig, ax = plt.subplots()
artists = []
im, = ax.plot([], [])
# グラフの範囲
ax.set_xlim(-1.0, 1.0)
ax.set_ylim(0.0, 1.0)
# f = x*xの定義用
F_main = np.arange(-1.0, 1.0, 0.01)
n_epoch = 800 # 学習回数
eta = 0.01 # ステップ幅
x_arr = []
f_arr = []
x_tor = torch.tensor([1.0], requires_grad=True)
for epoch in range(n_epoch):
# 最適化する関数の定義
f = func(x_tor)
# x_tor地点での勾配を計算
f.backward()
with torch.no_grad():
# 1.勾配法
# x_torから微小変化分を少しずつ引いて行って、
# 最小値に少しずつ近づけていく
x_tor = x_tor - eta * x_tor.grad
# 2.ここはアニメーション用の処理
f = x_tor[0] ** 2
x_arr.append(float(x_tor[0]))
f_arr.append(float(f))
x_tor.requires_grad = True
def update_anim(frame):
# gif保存するための処理
# FuncAnimation実行後、自動で繰り返し実行される。(frame = フレーム数)
ims = []
if frame == 0:
y = f_arr[frame]
x = x_arr[frame]
else:
y = [f_arr[frame-1],f_arr[frame]]
x = [x_arr[frame-1],x_arr[frame]]
ims.append(ax.plot(F_main ,F_main*F_main,color="b",alpha=0.2,lw=0.5))
ims.append(ax.plot(x ,y,lw=10,color="r"))
# im.set_data(x, y)
return ims
anim = FuncAnimation(fig, update_anim, blit=False,interval=50)
anim.save('GD_パターン1.gif', writer="pillow")
exit()
最適化の実装(最急降下法)
実装してみます。
なお、この項の目的は最急降下法を実装することそのものではなく、
「こうやって自作の最適化関数実装するんだー」というのを確認するための検証です。
また長々と書くのは何なので、要点だけ書きます。
optimizer = optim.SGD(Test_Conv.parameters(), lr=0.001, momentum=0.9)
pytorchでは、optimから様々な最適化手法を選択します。
各手法の実装は、$torch.optim.Optimizer$というクラスを継承することで作成されます。
裏を返せば、$torch.optim.Optimizer$の継承クラスを自作すれば簡単に自作できます。
ということで、先ほどと同様に$y=x^2$に対して最適化します。
この例ではニュートラルネットワークは使っていませんが、
私が定義した$SimpleGD$を同じように定義すれば、ニュートラルネットワークでも変わらず使えます。
↓↓↓全体のソース↓↓↓
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import numpy as np
import torch
import torchvision
import torchvision.transforms as transforms
class SimpleGD(torch.optim.Optimizer):
def __init__(self, params, lr):
defaults = dict(lr=lr)
super(SimpleGD, self).__init__(params, defaults)
@torch.no_grad()
def step(self, closure=None):
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
d_p = p.grad
# tensorの足し算
# p = p - d/dp(微小変化) * lr
# (lrは微小変化だけだと変化の幅が小さすぎるので掛け合わせている)
p.add_(d_p*-group['lr'])
return loss
def func(x):
return x[0] ** 2
fig, ax = plt.subplots()
artists = []
im, = ax.plot([], [])
# グラフの範囲
ax.set_xlim(-1.0, 1.0)
ax.set_ylim(0.0, 1.0)
# f = x*xの定義用
F_main = np.arange(-1.0, 1.0, 0.01)
n_epoch = 50 # 学習回数
eta = 0.01 # ステップ幅
x_tor = torch.tensor([1.0], requires_grad=True)
param=[x_tor]
optimizer = SimpleGD(param, lr=0.1)
for epoch in range(n_epoch):
optimizer.zero_grad()
# 最適化する関数の定義
f = func(x_tor)
# x_tor地点での勾配を計算
f.backward()
optimizer.step()
x_tor.requires_grad = True
# 徐々にy=x*xの最小値=0.0に向かっていく
# print(x_tor)
exit()
このうち、特に重要なのは、
自作の最適化関数を宣言した「class SimpleGD」の部分です。
class SimpleGD(torch.optim.Optimizer):
def __init__(self, params, lr):
defaults = dict(lr=lr)
super(SimpleGD, self).__init__(params, defaults)
@torch.no_grad()
def step(self, closure=None):
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
d_p = p.grad
# tensorの足し算
# p = p - d/dp(微小変化) * lr
# (lrは微小変化だけだと変化の幅が小さすぎるので掛け合わせている)
p.add_(d_p*-group['lr'])
return loss
詳しく見てみます。
まずinit部分について。
def __init__(self, params, lr):
defaults = dict(lr=lr)
super(SimpleGD, self).__init__(params, defaults)
lrというのは、微小変化分を差し引いていくときに、
微小変化だけだと変化の幅が小さすぎる・大きすぎるので、
微小変化にかけあわせてやるパラメータを指定しています。
SimpleGDではlrが必要だったのでここに宣言しました。
他にも必要な場合はinitの引数に追加して、dictの中にもしっかり宣言を追加して下さい。
@torch.no_grad()
def step(self, closure=None):
torch.optim.Optimizerクラス継承時に、宣言しなければならない関数です。
学習中にこの関数を呼び出すことで、最適化が行われます。
self.param_groupsは、SimpleGDのインスタンスを作成したときに渡したparamsです。
backward()で勾配(微小変化)が計算済みであれば、ここから勾配も取得できます。
d_p = p.grad
# tensorの足し算
# p = p - d/dp(微小変化) * lr
# (lrは微小変化だけだと変化の幅が小さすぎるので掛け合わせている)
p.add_(d_p*-group['lr'])
p.grad、すなわち微小変化分を取得し、
その微小変化分をp=テンソルに反映させています。
この操作により、徐々に徐々にパラメーターが最小値へと向かっていきます。
・・・・なお、最急降下法は微小分を引いてるだけなので、局所解に簡単に陥ります。
局所解。$y=x^2$のような凸がたくさんあるグラフを想像してください。
最急降下法は傾きが0になる場所を最小値とみなすので、
この凸の先っちょのどれかに到達すると必ず極値とみなしてしまいます。
このことから、この手法はどんなデータに対しても頑強ではないといえます。
おわりに
1章2章でなんとなくのネットワークの概要がすこしだけわかりました。
次回以降の予定としては、
一番勉強したかった点群系の機械学習の勉強、
特にPointNetについて勉強します。
それ以降は、RNN、オートエンコーダ、GAN 、DQNをざっくり勉強します。