全体像もまだ把握しきれていない著者が、メモ代わりに記載したものをまとめたものです。
Pytorchのチュートリアルの内容+αで調べた内容をまとめます。
今回は第1章です。
はじめに
インストールと、CNNの基本的な各層について勉強します。
32×32の行列のような大きな次元で計算すると
どんな計算をおこなっているかをイメージしづらいので
簡単な例で実際のコードを計算し、ある程度の計算式も記載するようにしました。
直観的な把握を目指します。
1-インストール
上記URLから自分のPCの環境を選択し、[Run this Command]のコマンドを実行します。
1-0.はじめてさわってみる
numpyと同じような感じで行列を出力してみます。
https://pytorch.org/tutorials/beginner/blitz/tensor_tutorial.html#sphx-glr-beginner-blitz-tensor-tutorial-py
x = torch.empty(5, 3)
print(x)
# 実行結果
tensor([[1.9349e-19, 4.5445e+30, 4.7429e+30],
[7.1354e+31, 7.1118e-04, 1.7444e+28],
[7.3909e+22, 4.5828e+30, 3.2483e+33],
[1.9690e-19, 6.8589e+22, 1.3340e+31],
[1.1708e-19, 7.2128e+22, 9.2216e+29]])
numpyっぽい。
1-1.勾配
$requires_grad$とすることで、ある地点での勾配を求められるそうです。
x = torch.tensor([1.0, 2.0], requires_grad=True)
例として、下記の2変数の関数に対する勾配を求めてみます。
f(x,y)=2x + y^2\\
勾配を式で求めると以下のような式になります。
\frac
{\partial f}
{\partial x}
=
2\\
\frac
{\partial f}
{\partial y}
=
2y\\
上式より、$x$方向の勾配は2、$y$方向の勾配は2yで決定されることがわかります。
(x,y)=(1,2)の地点での勾配は下記より(2,4)となります。
\frac
{\partial f}
{\partial x}
=
2\\
\frac
{\partial f}
{\partial y}
=
2*2=4\\
・・・という計算をやってくれるのがrequires_gradになります。
実際にpytorchでやったものが以下になります。
from __future__ import print_function
import torch
# 計算地点の準備
z = torch.tensor([1.0, 2.0], requires_grad=True)
# f(z)の準備
f = z[0]*2 + z[1]**2
# 微分の実行
f.backward()
print(z.grad)
# 実行結果
tensor([2., 4.])
1-2.ニュートラルネットワーク
https://pytorch.org/tutorials/beginner/blitz/neural_networks_tutorial.html
チュートリアルの次項でさっそくネットワークが定義されます。
import torch
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 1 input image channel, 6 output channels, 3x3 square convolution
# kernel
self.conv1 = nn.Conv2d(1, 6, 3)
self.conv2 = nn.Conv2d(6, 16, 3)
# an affine operation: y = Wx + b
self.fc1 = nn.Linear(16 * 6 * 6, 120) # 6*6 from image dimension
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# Max pooling over a (2, 2) window
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
# If the size is a square you can only specify a single number
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
size = x.size()[1:] # all dimensions except the batch dimension
num_features = 1
for s in size:
num_features *= s
return num_features
net = Net()
print(net)
params = list(net.parameters())
print(len(params))
print(params[0].size()) # conv1's .weight
input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)
net.zero_grad()
out.backward(torch.randn(1, 10))
いきなり走らせても「?」となるので、一つ一つ中身を見てみます。
クラスの継承
class Net(nn.Module):
def __init__(self):
# 各層を定義
def forward(self, x):
# 各層の処理を実行
nn.Moduleクラスを継承することで、
自由にネットワークの構成を定義することができるようです。
initにてクラスが初期化されるタイミングで各層の定義を行い、
forwardにて定義した層を呼び出してCNNの本幹の処理を呼び出します。
実際の流れとしては、
自分で定義したクラスのインスタンスが作成されたタイミングでforwardが実行されます。
forwardの処理
処理の本幹はforwardの処理内容になります。
サンプルソースを分解し、各層を一つずつ見てみます。
(活性化関数の説明は一旦飛ばします)
def forward(self, x):
# Max pooling over a (2, 2) window
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
# If the size is a square you can only specify a single number
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
↓↓↓↓↓↓↓↓↓↓↓↓↓
max_pool2d : プーリング層
Conv2d : 畳み込み層
Linear : 全結合層
pooling層(プーリング層)
max_pool2dを単体で実行してみます。
import torch
import torch.nn as nn
import numpy as np
import torch.nn.functional as F
class Test_Pooling(nn.Module):
def __init__(self):
super(Test_Pooling, self).__init__()
def forward(self, x):
print("Before")
print("size : \t",x.size())
print("data : \n",x.to('cpu').detach().numpy().copy())
print("\n")
x = F.max_pool2d(x, (2, 2))
print("After")
print("size : \t",x.size())
print("data : \n",x.to('cpu').detach().numpy().copy())
print("\n")
return x
net = Test_Pooling()
# 入力
nparr = np.array([1,2,3,4]).astype(np.float32).reshape(2,2)
nparr = np.block([[nparr,nparr],[nparr,nparr]]).reshape(1,1,4,4)
input = torch.from_numpy(nparr).clone()
# 出力
out = net(input)
# 実行結果
Before
size : torch.Size([1, 1, 4, 4])
data :
[[[[1. 2. 1. 2.]
[3. 4. 3. 4.]
[1. 2. 1. 2.]
[3. 4. 3. 4.]]]]
After
size : torch.Size([1, 1, 2, 2])
data :
[[[[4. 4.]
[4. 4.]]]]
入力データは以下の通りです。
input = \begin{pmatrix}
1 & 2 & 1 & 2\\
3 & 4 & 3 & 4\\
1 & 2 & 1 & 2\\
3 & 4 & 3 & 4\\
\end{pmatrix}\\
max_pool2dの動作としては、引数で指定した(2,2)の範囲内で、
最大の値を抽出し行列として値を返します。
上記の入力行列に適用すれば、1、2,3,4の部分行列に対して実行されるので、
その結果、4が4つ並んだ(2,2)が出力されます。
プーリングを行う目的は主に2つ。
1.次元の削減
2.移動・回転の不変性の確保
1つは次元の削減。
見てわかる通り、16個の数値が4個に削減されています。
画像数百枚を処理すると考えれば、何倍も一気に処理の短縮が期待できそうです。
(削減された分情報は失われるので、
どこまでプーリングしてよいかは物によって違うのでしょうが。)
もう1つは不変性。
入力画像が回転していたり、位置がずれている場合は当然起こりえます。
そういったケースにもある程度の保証ができるものがプーリングと思われます。
例えば、グレースケールの画像のピクセルの配列が、
一方では、$(0,0,0,0,1,2,3,4,5,1,2)$、
もう一方は$(0,1,2,3,4,5,1,2,3,4,5)$と
片方の画像が同じものを映しているのに横にずれていた場合を考えた場合。
仮に(1,12)の横長の範囲でマックスプーリングを行えば、
どちらの画像でも(5)が出力され、「両者が同じ数値を示す」、すなわち、
画像の移動に関係なく特徴の手がかりを見つけることが可能になります。
(・・・と、調べたことを書きましたが、1の目的のほうはともかく、
果たして2のほうはどれくらい効果的が実際に期待できるのか、
画像に対しては若干信用しきれていない印象があります。(順不同な点群ならともかく))
conv層(畳み込み層)その1
畳み込みのイメージ及び、実際にどんな計算をおこなっているかを整理します。
「畳み込み」とは何か。
誤解を恐れずに言えば、畳み込みを行うことで、
特徴的な部分を強調して抽出するために行う、という認識です。
例えばラプラシアンフィルターという5×5のフィルターを
畳み込み積分すると、上記の画像のようにエッジが強調された画像が出力されます。
エッジ部分の特徴が強調されて抽出されるわけですね。
(参考:https://desktop.arcgis.com/ja/arcmap/10.3/manage-data/raster-and-images/convolution-function.htm)
計算式としてはどのような計算が行われるかについては、
音声処理だとわかりづらいですが、画像の場合は視覚的にわかりやすいです。(↓)
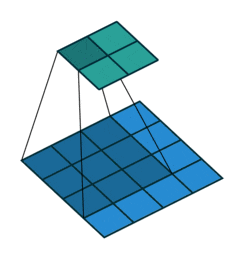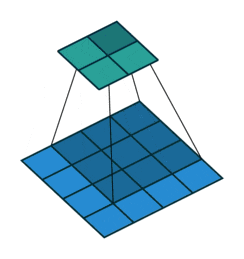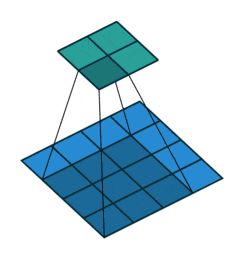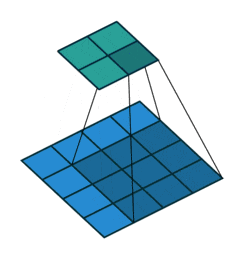
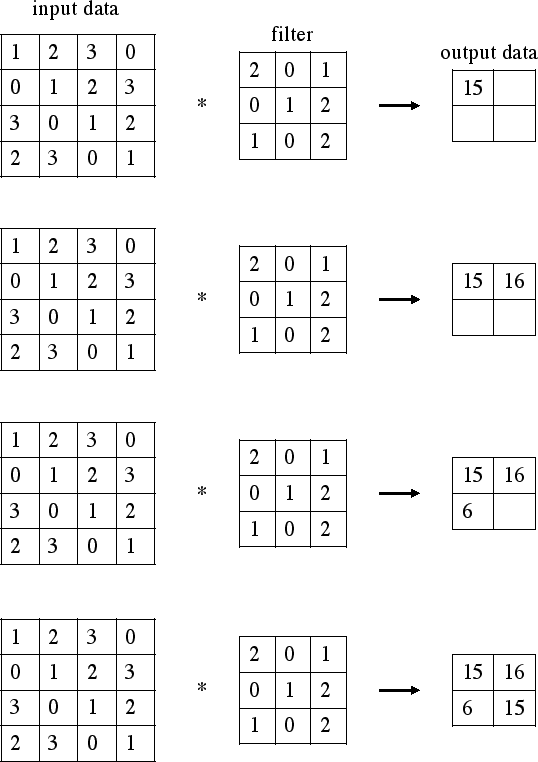
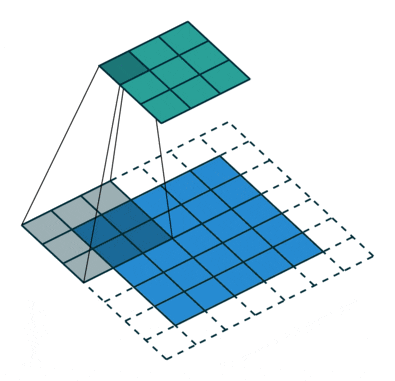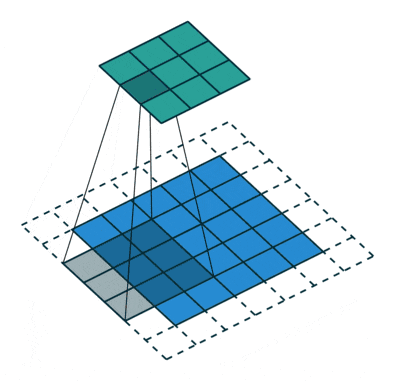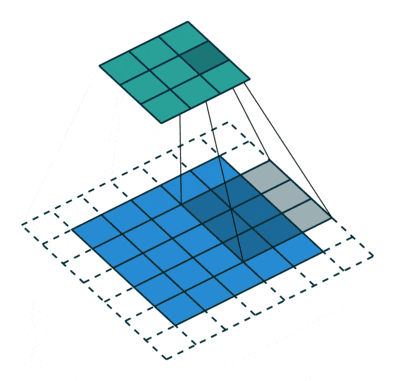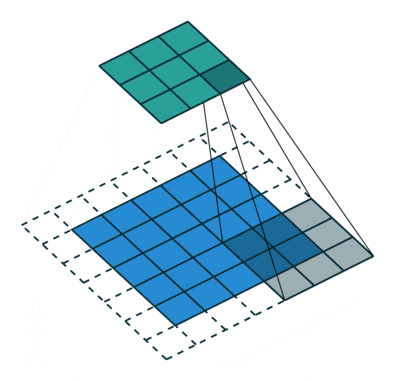
画像領域の畳み込みの場合は、ターゲットの画像(青い行列)のピクセルに対して、
上記の動画のように順々に「カーネル」(緑の行列)を当てはめて計算していきます。
計算としては上記の画像の例で言えば、
[input data]の(2,2)の1のピクセルを中心にカーネルを当てはめて。
(1*2)+(2*0)+(3*1)+(0*0)+(1*1)+(2*2)+(3*1)+(0*0)+(1*2)=15
と、同じ位置にあるもの同士を乗算したものを足していきます。
図の例で言えば、3×3のフィルターを隙間なく当てはめようとすると、
4×4の[output data]が計算されます。
ということでこれらを踏まえてソースをいじりつつ、
計算の様子を少しだけみてみます。
class Test_Conv(nn.Module):
kernel_filter = None
def __init__(self):
super(Test_Conv, self).__init__()
# self.conv = nn.Conv2d(1, 1, 3)
ksize = 4
self.conv = nn.Conv2d(
in_channels=1,
out_channels=1,
kernel_size=4,
bias=False)
self.kernel_filter = self.conv.weight.data.numpy().reshape(ksize,ksize)
def forward(self, x):
print("Before")
print("size : \t",x.size())
print("data : \n",x.to('cpu').detach().numpy().copy())
print("\n")
print("Calc Self Conv")
x_np = x.to('cpu').detach().numpy().copy().reshape(4,4)
calc_conv = 0 ;
for col in range(self.kernel_filter.shape[0]):
for row in range(self.kernel_filter.shape[1]):
calc_conv += self.kernel_filter[row][col] * x_np[row][col]
print("kernel filter :")
print(self.kernel_filter )
print("data : \n",calc_conv)
print("\n")
x = self.conv(x)
print("After")
print("size : \t",x.size())
print("data : \n",x.to('cpu').detach().numpy().copy())
print("\n")
return x
net = Test_Conv()
# 入力
nparr = np.array([1,2,3,4]).astype(np.float32).reshape(2,2)
nparr = np.block([[nparr,nparr],[nparr,nparr]]).reshape(1,1,4,4)
input = torch.from_numpy(nparr).clone()
# 出力
out = net(input)
exit()
エッジを抽出するラプラシアンフィルターでは、
固定のカーネルフィルターを適用させていました。
ですがpytorchのConv2dで自動で生成されるカーネルフィルターは、
実行のたびにランダムに値が変わるようです。
(どんな計算をしてどんな意図でconv2dがこのフィルターを計算しているかは未調査です。
フィルタ―は意図的に設定することはできないんでしょうか?)
さて、出力結果は以下の通りとなりました。
# 実行結果
Before
size : torch.Size([1, 1, 4, 4])
data :
[[[[1. 2. 1. 2.]
[3. 4. 3. 4.]
[1. 2. 1. 2.]
[3. 4. 3. 4.]]]]
Calc Self Conv
kernel filter :
[[-0.03335193 -0.05553913 0.10690624 -0.0219309 ]
[-0.02052614 0.23662615 -0.07596081 -0.04400161]
[ 0.19031712 -0.06902602 -0.24611491 -0.06604707]
[-0.05149609 -0.08155683 0.06496871 -0.15480098]]
data :
-0.8313058316707611
After
size : torch.Size([1, 1, 1, 1])
data :
[[[[-0.8313058]]]]
[Before]の[dara]が、
入力データ。先ほどのアニメーションで言うところの青い行列です。
そして[After]。
[dara]が畳み込み層で計算された結果です。
[-0.8313058]とありますね。
次に[Calc Self Conv]を見てみます。
ここで、上述の計算を試しに手計算してみました。
Conv2dの宣言時にkernel_size=4と指定したので、
計算のもとになるkernel filter には4×4の行列で出力されていることがわかります。
これが先ほどのアニメーションでいうところの緑の行列です。
さて、それでは手計算の結果とconv2dの結果を比べてみます。
[Calc Self Conv]と[After]の[data]のところを見ると、
数値がほぼほぼ同じことがわかりますね。
このようなイメージで、畳み込み層は計算が行われます。
なおこの例は計算を簡易にするためにかなり簡易にしているので、
次以降でもう少し掘り下げます。
conv層(畳み込み層)その2
もう少し勉強します。
畳み込みがどんな計算をおこなっているかまでは、なんとなくわかりました。
次は実際の計算を行ったときに関わってくるパラメーターをもう少し見てみます。
conv2dには主に以下のパラメータが存在します。
in_channels
out_channels
kernel_size
stride
padding
bias
直観的な説明を行うために、
実際のコードで一つずつ見てみます。
in_channels
in_channelsには、1つのデータ辺りの次元数をセットします。
data :
[[[[0. 1. 0. 1.]
[0. 0. 0. 0.]
[0. 1. 0. 1.]
[0. 0. 0. 0.]]]]
上記のデータを例に見てみます。
画像でいうなればこのデータはグレースケール画像、
チャンネル数(色の数)は1つだけのデータです。
このようなデータなら、「1」をセットします。
RGBの3次元のデータなら「3」、
点群のように位置とRGBを持っているなら「6」と入力します。
out_channels
out_channelsには出力するデータの次元数が出力されます。
ここで指定した数だけカーネルフィルターが生成され、
フィルターの適用結果が指定した数だけ返ってきます。
すなわち、言い換えるならここの次元が多いほど、
その次元の数だけ作成されたフィルターによって特徴が抽出され、
様々な特性を持った特徴を数量として抽出できるわけです。
たとえば、
動物の特徴を抽出するフィルター、
人間の特徴を抽出するフィルター、
コップの特徴を抽出するフィルター、
と様々な特徴を抽出するフィルターの数をここで宣言するわけですね。
(この説明だけ聞くと、多ければ多いほど良さそうに思えてきます。
直観的には、特徴を細かく抽出しすぎると、
Aさん・Bさんのような細かい分類はできても、
人間と言うくくりで分類できない等の問題が起きそうな気がします
(個人的な実践を伴わないイメージ))
stride
strideは、フィルターを書けるときの移動の幅を指します。

この画像で言えば、1つずつ移動しているのでストライドは「1」ですね。
コードでもう少しこの動きを見てみます。
class Test_Conv2(nn.Module):
kernel_filter = None
def __init__(self):
super(Test_Conv2, self).__init__()
self.conv = nn.Conv2d(
in_channels=1,
out_channels=2,
kernel_size=2,
stride=2,
padding=0,
bias=False)
self.kernel_filter = self.conv.weight.data.numpy()
def forward(self, x):
print("Before")
print("size : \t",x.size())
print("data : \n",x.to('cpu').detach().numpy().copy())
print("\n")
print("Calc Self Conv")
print("kernel filter :")
print(self.kernel_filter )
print("\n")
x = self.conv(x)
print("After")
print("size : \t",x.size())
print("data : \n",x.to('cpu').detach().numpy().copy())
print("\n")
return x
net = Test_Conv2()
# 入力
nparr = np.array([0,1,0,0]).astype(np.float32).reshape(2,2)
nparr = np.block([[nparr,nparr],[nparr,nparr]]).reshape(1,1,4,4)
input = torch.from_numpy(nparr).clone()
# 出力
out = net(input)
exit()
# 実行結果
Before
size : torch.Size([1, 1, 4, 4])
data :
[[[[0. 1. 0. 1.]
[0. 0. 0. 0.]
[0. 1. 0. 1.]
[0. 0. 0. 0.]]]]
Calc Self Conv
kernel filter :
[[[[-0.07809174 -0.39049476]
[-0.00448102 -0.09000683]]]
[[[ 0.03750324 0.12070286]
[-0.06378353 0.22772777]]]]
After
size : torch.Size([1, 2, 2, 2])
data :
[[[[-0.39049476 -0.39049476]
[-0.39049476 -0.39049476]]
[[ 0.12070286 0.12070286]
[ 0.12070286 0.12070286]]]]
ストライドを「2」と設定しました。
2つずつずれるので、計算としては、
[Before]の[data]と
[Calc Self Conv]の[kernel filter]とを
掛け合わされることになります。
input = \begin{pmatrix}
0 & 1 \\
0 & 0
\end{pmatrix}\\\\
filter = \begin{pmatrix}
-0.07809174 & -0.39049476 \\
-0.00448102 & -0.09000683
\end{pmatrix}\\
実際に2個ずつずれているのか、
実行結果で確認します。
入力データは上記の[input]の部分行列が4つ並んだ行列です。
このような入力データに対して(2,2)の[filter]を当てはめようとすれば、
[input]の部分行列にピッタリ当てはまるように4回掛け合わせることになります。
output = \begin{pmatrix}
-0.39049476 & -0.39049476 \\
-0.39049476 & -0.39049476
\end{pmatrix}\\
したがって、
[input]の部分行列と[filter]の行列との畳み込みが4回行われるので、
[input]の部分行列が唯一[1]担っている箇所のフィルターの数値が4回出力されますね。
したがって、[output]のような結果として畳み込みが計算されます。
以上より、
2つずつピクセルがズレて畳み込みが行われる様子がなんとなくわかったかと思います。
padding
特に明言はしませんでしたが、フィルターをストライドさせるとき、
フィルターがちょうど画像の中に納まる範囲でフィルターを動かす前提で説明しました。

この画像で言えば、青い画像のピクセルの中央付近、
(1,1)(1,2)(2,1)(2,2)を中心としてフィルターを当てていますね。
(0,0)の左上の位置にフィルターを当てはめようとすると、
上のほうが重ならなくて、計算できなくなってしまうことが予想できます。
画像の中央部分は等しくフィルターで計算されているのに、
画像の端の部分はフィルターがかけられていない、という状態が発生する、
すなわち、これは端の部分の特徴が抽出できていない状態です。
なので、両端に[0]の仮想的な列・行を追加して計算することで、
端の部分も計算するのが「パディング」という考え方になります。
bias
出力結果のすべての要素に値が加算されるだけです。
各フィルターごとに重要度の優劣を決めるのにつかったりするんでしょうか?
あるいは逆に、小さな特徴しか拾えないものを
他の特徴と同じように扱うために大きくする、とかあるんでしょうか?
出力結果
パラメータによって畳み込みの出力結果の次元は変化します。
conv2dのパラメータをもとに、次元がどのように変わるか見てみます。
in_channels
out_channels
kernel_size
stride
padding
bias
例1 入力データ=(次元=1,(4×4))) / カーネルサイズ=2 / パディング=0
in_channels=1\\
out_channels=1\\
kernel_size=2\\
stride=2\\
padding=0\\
bias=0\\
\\
\\
input = \begin{pmatrix}
0 & 1 & 0 & 1\\
0 & 0 & 0 & 0\\
0 & 1 & 0 & 1\\
0 & 0 & 0 & 0
\end{pmatrix}\\\\
filter = \begin{pmatrix}
-0.07809174 & -0.39049476 \\
-0.00448102 & -0.09000683
\end{pmatrix}\\
この場合、(2,2)のフィルターが(4,4)の入力データを
2個ずつ移動してピッタリ沿うように移動します。
出力結果は2×2です。
例2 入力データ=(次元=1,(4×4))) / カーネルサイズ=3 / パディング=0
in_channels=1\\
out_channels=1\\
kernel_size=3\\
stride=2\\
padding=0\\
bias=0\\
\\
\\
input = \begin{pmatrix}
0 & 1 & 0 & 1\\
0 & 0 & 0 & 0\\
0 & 1 & 0 & 1\\
0 & 0 & 0 & 0
\end{pmatrix}\\\\
filter = \begin{pmatrix}
-0.41127872
\end{pmatrix}\\
この場合、(3,3)のフィルターが(4,4)の入力データを2個ずつ移動します。
左上から計算されるので、入力データが(1,1)の位置を中心として、
フィルターの畳み込みが行われます。
そこからストライドが2なので横に2ずれると、
次の計算の中心位置は(1,3)。右端っこなので、
フィルターが全て収まりません。
縦に対しても2こずつずれるので、
結果的にはストライドの操作を繰り返しても1回しか畳み込みが行われません。
したがって、結果は1つだけになります。
例2 入力データ=(次元=1,(4×4))) / カーネルサイズ=3 / パディング=1
in_channels=1\\
out_channels=1\\
kernel_size=3\\
stride=2\\
padding=1\\
bias=0\\
\\
\\
input = \begin{pmatrix}
0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 1 & 0 & 1 & 0\\
0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 1 & 0 & 1 & 0\\
0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0\\
\end{pmatrix}\\\\
filter = \begin{pmatrix}
0.08725476 & 0.4106578 \\
0.08725476 & 0.4106578 \\
\end{pmatrix}\\
0が両端に1行/列ずつパディングされました。
左上を基準に、3×3のフィルターが収まる位置で計算していくと、
(1,1)(1,3)(3,1)(3,3)を中心として4回計算されます。
したがって、出力結果は2×2です。
Linear層(全結合層)
全結合層。
やってることは非常にシンプルで、
畳み込み層などで抽出された様々な特徴を
1つにまとめましょう?ということをやっています。
誤解を恐れずイメージで言うなら、
「赤い四角」。「青い四角」、「それ以外」を判別しようとした場合を考えます。
四角の特徴だけを抽出しても、赤と青は識別できないので、
色の特徴もあわせてみないといけません。
よって、四角の特徴と色の特徴、複数の特徴を合わせてみるために行うのが、
全結合層と私は認識しています。
y = xA^T \\
やっている計算もシンプルで、
入力$x$に対して線形変換$A$を適用させて、
出力として$y$を計算するだけです。
y = xA^T \\
⇔\\
\begin{pmatrix}
y_1 \\
y_2 \\
\end{pmatrix}
=
\begin{pmatrix}
A_{00} & A_{01} \\
A_{10} & A_{11} \\
\end{pmatrix}
\begin{pmatrix}
x_1 \\
x_2 \\
\end{pmatrix}\\
⇔\\
\begin{pmatrix}
y_1 = A_{00} x_1 + A_{01}x_2\\
y_2 = A_{10} x_1 + A_{11}x_2 \\
\end{pmatrix}\\
もう少し直観的な説明を試みます。
上式は、2次元の小さなデータに対して先ほどの式を展開させたものです。
入力データ$x$とは、すなわち画像から特徴を抽出した数値です。
式では$x_1$と$x_2$の値をもっていますが、
これを先ほどの例に習い、
「画像から四角い特徴を抽出した結果」
「画像から色の特徴を抽出した結果」
とします。
上述の通り、それぞれ単体だけでは
赤い四角か青い四角かはわかりません。
合わせて結果を見ないといけません。
それを踏まえて最期の式をみると、
$x_1$と$x_2$が統合されていることがわかります。
一応、コードでも動作を見てます。
class Test_Linear(nn.Module):
fc_filter = None
def __init__(self):
super(Test_Linear, self).__init__()
self.conv = nn.Conv2d(
in_channels=1,
out_channels=2,
kernel_size=4,
stride=2,
padding=0)
self.kernel_filter = self.conv.weight.data.numpy()
self.fc = nn.Linear(in_features=1,
out_features=1,
bias=False)
self.fc_filter = self.fc.weight.data.numpy()
print(self.fc_filter)
def forward(self, x):
nparr = np.array( [[[[1.0]],[[100.0]]]]).astype(np.float32)
input = torch.from_numpy(nparr).clone()
x = input
print("Before")
print("size : \t",x.size())
print("data : \n",x.to('cpu').detach().numpy().copy())
print("\n")
x = self.fc(x)
print("After Linear")
print("size : \t",x.size())
print("data : \n",x.to('cpu').detach().numpy().copy())
print("\n")
return x
net = Test_Linear()
# 入力
nparr = np.array([0,1,0,0]).astype(np.float32).reshape(2,2)
nparr = np.block([[nparr,nparr],[nparr,nparr]]).reshape(1,1,4,4)
input = torch.from_numpy(nparr).clone()
# 出力
out = net(input)
exit()
# 実行結果
[[0.04909718]]
Before
size : torch.Size([1, 2, 1, 1])
data :
[[[[ 1.]]
[[100.]]]]
After Linear
size : torch.Size([1, 2, 1, 1])
data :
[[[[0.04909718]]
[[4.909718 ]]]]
めちゃくちゃシンプルです。
$A=[0.04909718]$
$x=[1,100]^T$
を$y = xA^T$にしたがって計算し、
$y=[0.04909718,4.909718]^T$
を出力しているだけです。
ちなみにout_features=2として、
出力される次元を増やすと、
# 実行結果
[[-0.5130856]
[ 0.6920992]]
Before
size : torch.Size([1, 2, 1, 1])
data :
[[[[ 1.]]
[[100.]]]]
After Linear
size : torch.Size([1, 2, 1, 2])
data :
[[[[ -0.5130856 0.6920992]]
[[-51.30856 69.20992 ]]]]
Aの次元が一つ増えて、
$A=[-0.5130856,0.6920992]$
となり、
出力される$y$もさっきの結果にもう一つ追加される形で出力されます。
ここまでの内容まとめ
https://pytorch.org/tutorials/beginner/blitz/neural_networks_tutorial.html
pytorchのサンプルソースにあるネットワークの構成を、
めちゃくちゃざっくり流れを分析すると、
1.畳み込み層で特徴を抽出し、
2.プーリング層や活性化関数で(このページでは触れてない)抽出した特徴を整理し、
3.最終的には結合層で統合
という流れであることがわかります。
ここまでの内容で、我々は特徴を数値として獲得することができました。
しかしこれだけでは識別処理はできません。
これまでの内容を使えば、
AさんとBさんの特徴は取得できますが、
仮にAかBかわからない人がやってきたとき、
その正体不明人の特徴がA,Bどちらの物か判断する必要があります。
1-2.損失関数
これまでの内容に記載したネットワークですでに特徴の抽出は可能です。
どちゃくそシンプルな例で識別をしてみます。
class Test_Conv(nn.Module):
kernel_filter = None
def __init__(self):
super(Test_Conv, self).__init__()
# self.conv = nn.Conv2d(1, 1, 3)
ksize = 4
self.conv = nn.Conv2d(
in_channels=1,
out_channels=1,
kernel_size=4,
bias=False)
self.kernel_filter = self.conv.weight.data.numpy().reshape(ksize,ksize)
def forward(self, x):
x = self.conv(x)
return x
net = Test_Conv()
# 入力
nparr = np.array([0,1,0,0]).astype(np.float32).reshape(2,2)
nparr = np.block([[nparr,nparr],[nparr,nparr]]).reshape(1,1,4,4)
input = torch.from_numpy(nparr).clone()
print("*****学習フェーズ*****")
print("ネットワーク学習用の入力データ")
print(input)
print("\n")
# 出力
out = net(input)
# ターゲット入力 #同じデータを入力
out_target1 = net(input)
criterion = nn.MSELoss()
loss = criterion(out, out_target1)
print("*****評価フェーズ*****")
print("同じデータを入力")
print("input:")
print(input)
print("評価",loss)
print("\n")
# ターゲット入力 #ちょっと違うデータを入力
nparr2 = np.array([0,2,0,0]).astype(np.float32).reshape(2,2)
nparr2 = np.block([[nparr2,nparr2],[nparr2,nparr2]]).reshape(1,1,4,4)
input2 = torch.from_numpy(nparr2).clone()
out_target2 = net(input2)
criterion = nn.MSELoss()
loss = criterion(out, out_target2)
print("ちょっと違うデータを入力")
print("input:")
print(input2)
print("評価",loss)
print("\n")
# ターゲット入力 #ぜんぜん違うデータを入力
nparr3 = np.array([10,122,1000,200]).astype(np.float32).reshape(2,2)
nparr3 = np.block([[nparr3,nparr3],[nparr3,nparr3]]).reshape(1,1,4,4)
input3 = torch.from_numpy(nparr3).clone()
out_target3 = net(input3)
criterion = nn.MSELoss()
loss = criterion(out, out_target3)
print("ぜんぜん違うデータを入力")
print("input:")
print(input3)
print("評価",loss)
print("\n")
# 実行結果
*****学習フェーズ*****
ネットワーク学習用の入力データ
tensor([[[[0., 1., 0., 1.],
[0., 0., 0., 0.],
[0., 1., 0., 1.],
[0., 0., 0., 0.]]]])
*****評価フェーズ*****
同じデータを入力
input:
tensor([[[[0., 1., 0., 1.],
[0., 0., 0., 0.],
[0., 1., 0., 1.],
[0., 0., 0., 0.]]]])
評価 tensor(0., grad_fn=<MseLossBackward>)
ちょっと違うデータを入力
input:
tensor([[[[0., 2., 0., 2.],
[0., 0., 0., 0.],
[0., 2., 0., 2.],
[0., 0., 0., 0.]]]])
評価 tensor(0.4581, grad_fn=<MseLossBackward>)
ぜんぜん違うデータを入力
input:
tensor([[[[ 10., 122., 10., 122.],
[1000., 200., 1000., 200.],
[ 10., 122., 10., 122.],
[1000., 200., 1000., 200.]]]])
評価 tensor(58437.6680, grad_fn=<MseLossBackward>)
特に説明することもないのですが、
out = net(input)
out_target3 = net(input3)
各入力データを作成したネットワークに入力して特徴を計算し、
(out,out_target3にはconv2dで計算した行列が入っています。)
# 評価方法を定義
criterion = nn.MSELoss()
# 評価実行
loss = criterion(out, out_target3)
評価方法を定義(ここでは平均二乗誤差)し、評価する。
特徴が近ければ値は0に近くなるし、
特徴が遠ければ値は大きくなります。