最初に

　こんにちは、CodeNextに所属しています、@aiskoaskosdです。Chainerには普段からお世話になっていますので、恩返しができたら良いなと思い、記事を書かせていただきました。
　今日はここ1~2年で話題になった画像認識モデルを中心に、実装公開・いくつかの論文内容の説明をしていきます。2013年以前の論文もいくつか例外的に実装しています。24個中、22個のモデルの実装をChainerで行いました。残念ながら12月22日現在で、全ての実装とcifar10による検証が終わりませんでした。逐次更新していきます。
　間違った解釈をしている部分や実装の間違いがあると思います。その際は、教えていただけると非常にうれしいです。

論文

1. Netowork In Network
2. Very Deep Convolutional Networks for Large-Scale Image Recognition
3. Going deeper with convolutions
4. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
5. Rethinking the Inception Architecture for Computer Vision
6. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
7. Training Very Deep Networks
8. Deep Residual Learning for Image Recognition
9. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning
10. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size
11. Identity Mappings in Deep Residual Networks
12. Resnet in Resnet: Generalizing Residual Architectures
13. Deep Networks with Stochastic Depth
14. Swapout: Learning an ensemble of deep architectures
15. Wide Residual Networks
16. FractalNet: Ultra-Deep Neural Networks without Residuals
17. Weighted Residuals for Very Deep Networks
18. Residual Networks of Residual Networks: Multilevel Residual Networks
19. Densely Connected Convolutional Networks
20. Xception: Deep Learning with Depthwise Separable Convolutions
21. Deep Pyramidal Residual Networks
22. Neural Architecture Search with Reinforcement Learning
23. Aggregated Residual Transformations for Deep Neural Networks
24. Deep Pyramidal Residual Networks with Separated Stochastic Depth

パラメータ数は基本的に実際に実装したモデルから算出されおり、畳み込み層およびFC層のバイアス項を除いた重みの合計を計算しています。
日付はarxivの初版の投稿日となっています。
表の読み方は以下のようになります。
$\phi$(cifar 10 total accuracy 実装): 実装がまだ終わってない
$\times$(cifar 10 total accuracy 実装): 実装の検証はまだ
$\bigtriangleup$(cifar 10 total accuracy 実装): 実装の検証はしたが、論文に記述する精度に達しなかった
$\bigcirc$(cifar 10 total accuracy 実装): 実装の検証結果が、論文に記述する精度とほぼ一致
$\times$(cifar 10 total accuracy 論文): 論文内に記述がない
$\times$(imagenet top-5 error): 論文内に記述がない

紹介論文	日付	モデル	パラメータ数($10^6$)	cifar10 total accuracy 論文(%)	cifar10 total accuracy 実装	imagenet top-5 error(%)
1	131116	Caffe実装参考	0.1	91.19	$\bigtriangleup$(90.10)	$\times$
1	131116	Caffe実装参考 with BN	0.1	論文が存在しない	91.52%	論文が存在しない
2	140904	モデルA	129	$\times$	92.1(モデルA)	6.8(モデルE)
3	140917	googlenet	6	$\times$	91.33%	6.67
4	150211	inceptionv2	10	$\times$	94.89%	4.9
5	151202	inceptionv3(参考)	22.5	$\times$	94.74%	3.58
6	150206	model A	43.9(sppの代わりにglobal average pooling)	$\times$	94.98%	4.94
7	150722	Highway(Fitnet19)	2.8	92.46	$\bigcirc$(93.35%,ただしBNがついたり、higway部分の構成が異なります)	$\times$
8	151210	ResNet110	1.6	93.57	$\bigcirc$(93.34%)	3.57
9	160223	inception v4	$\times$	$\times$	$\phi$	3.1
10	160224	Squeezenet with BN	0.7	82%(alexnet without data augmentation)	$\bigcirc$(92.63%)	17.5(without BN and single)
11	160316	ResNet164	1.6	94.54	$\bigcirc$(94.39%)	4.8(single)
12	160325	18-layer + wide RiR	9.5	94.99	$\bigtriangleup$(94.43%)	$\times$
13	160330	ResNet110	1.7	94.75	$\bigcirc$(94.76%)	$\times$
14	160520	Swapout v2(32)W×4	7.1	95.24	$\bigcirc$(95.34%)	$\times$
15	160523	WRN28-10	36.2	96.0	$\bigcirc$(95.76%)	$\times$
16	160524	20 layers	33.7	95.41	$\bigtriangleup$(93.77%)	7.39%(FractalNet-34)
17	160528	WResNet-d	19.1	95.3	$\times$	$\times$
18	160809	RoR-3-WRN58-4	13.6	96.23	$\times$	$\times$
19	160825	k=24, depth=100	27.0	96.26	$\bigcirc$ 95.12%(k=12, depth=40)	$\times$
20	161007	xception	$\times$	$\times$	$\phi$	5.5(single)
21	161010	$\alpha = 270$	28.4	96.23	$\bigcirc$(95.9%)	4.7($\alpha = 450$)
22	161105	depth=49	32(論文より)	96.16	$\bigtriangleup$90.35(Appendix A: 4.1M)	$\times$
23	161116	ResNeXt-29, 16×64d	68.3	96.42	$\bigcirc$(95.72%: 2x64d)	$\times$
24	161205	depth=182, $\alpha$=150	16.5	96.69	$\times$	$\times$

実装

検証が終わっていないモデルの使用は気をつけてください

cifar10の数値感覚

　現時点で97%以上ではSoTAになると思います。僕が知っている限り、最高精度は96.69%です。そろそろcifar100か別のデータセットを評価の軸にするべきかもしれません。

感想

　22から出たgoogleの論文がとても衝撃的で、ここから何か発展していくような可能性が少しあると個人的に思っています(根拠はないです)。22はgpu800個とRNN+policy gradientでネットワークの探索を行っていて、cifar10で96.16%を記録しています。これでmnistで99%とかだったら、ふーんで終わりなんですが、cifar10でSoTAに近い値が出ているのがとても驚異的です。データにネットワーク構造を決めさせるというのは、とても魅力的なアイデアで、DNNの登場を彷彿させます(特徴量設計をデータにさせる)。
　それとここでは紹介しなかったのですが、HyperNetworksがとても興味深く、読んだ時に衝撃を受けたのを覚えています。HyperNetworksはネットワークの重みを生成するネットワークで、これから何か融合or発展してきそうな技術です。
　何もなければ順当にResブロックの改造・Resブロックのつながり方が今後発展していくように思えますが、どうなるのでしょうか。

　いくつか論文紹介

4. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

　Batch normalizationは一言で言うと、”バッチ間でそれぞれの入力をチャンネルレベルで正規化する”です。このBatch Normalizationはとても有益です。ネットワークにいれない理由がないです。収束もはやくなりますし、精度もやや上がります。
　Batch Normalizationは大事なのでがっつり説明します。まずBatch Normalizationを行う動機の元となる、内部共変量シフト(internal covariate shift)という現象の説明と、具体的なアルゴリズムについて説明していきます。

内部共変量シフト(internal covariate shift)

　レイヤー$l_{i}$の重みが誤差逆伝搬法で変化したとします。すると、その重みを用いて出力される出力値の分布（出力の性質）は変化します。レイヤー$l_{i+1}$は、変化した出力値の分布に対応した上で、適切な非線形写像を学習しなくてはいけません。ここの何が問題かというと、変化した出力の分布に適応するための学習に大きな労力が割かれるため、識別のための非線形写像の学習が非常に遅くなるということです。この現象のことを内部共変量シフトと、論文内では定義されています。
　この内部共変量シフトは、学習が停滞する原因となっています。仮にSGDの学習係数を大きく設定したとします。すると、レイヤー$l_{i}$の重みが大きく変化します。そのためレイヤー$l_{i+1}$は、変化した出力値に適応できず(もしくは適応するのにとてつもない時間がかかってしまい)、学習が停滞してしまいます。結果として学習をするために学習係数を小さく設定しなくてはならず、今度は学習はしても学習の収束が遅くなってしまいます。あっちを立てれば、こっちが立たずといった感じです。
　この内部共変量シフトはモデルが深いほど深刻な問題となります。低層の出力変化がわずかだとしても、上層で増幅されて、ささいな変化が大きな変化となってしまったりするからです。バタフライ・エフェクトみたいですね。
　これに対する解決策は非常に単純です。出力値の分布が変化してしまうなら、同じ分布になるように毎回調整してあげれば良いわけです。BN(Batch Normalization)は入力を正規化(平均0、分散1)し、出力します。そのため、BNの出力を入力とする場合には、出力の分布が安定したものとなり、出力分布の変化に対応するための学習の必要性が軽減します。本質的にやらなきゃいけない非線形写像の学習に集中することができ、結果として学習がはやく収束します。さらに、分布が安定しているので、学習係数を大きく設定することができます。これもまた、学習がはやく収束することに大きな貢献をします。このBNを入れると、GoogLeNetの学習時間が7%程度になります。すごいですね。

Batch Normalizationのアルゴリズム

　入力を$x_{i,cxy}$とします。これはバッチ$i$におけるチャンネル$c$の$(x,y)$の位置にある入力ということを意味します。チャンネル$c$での平均を$\mu_{c}$、チャンネル$c$での分散を$\sigma_{c}^2$とします。するとバッチ数を$m$、入力の高さ$Y$、入力の幅を$X$としたとき、$\mu_{c}$と$\sigma_{c}^2$は以下のように表せます。

$$\begin{equation}
\mu_{c} = \frac{1}{mXY}\sum_{i=1}^{m} \sum_{y=1}^{Y} \sum_{x=1}^{X} x_{i,cxy} \tag{4.1}
\end{equation}$$

$$\begin{equation}
\sigma_{c}^2 = \frac{1}{mXY}\sum_{i=1}^{m} \sum_{y=1}^{Y} \sum_{x=1}^{X} (x_{i,cxy} -\mu_c)^2 \tag{4.2}
\end{equation}$$

　式(4.1)、(4.2)を見ると、バッチ間で各チャンネルごとに平均$\mu_{c}$と分散$\sigma_{c}^2$を計算していることがわかります。これは学習ではありません。
　次にそれぞれの入力$x_{i,cxy}$を正規化したものを$\hat{x_{i,cxy}}$とします。ここでスケール$\gamma_{c}$とシフト$\beta_{c}$を各チャンネル毎に定義します。$\gamma_{c}$とシフト$\beta_{c}$は誤差逆伝搬法で学習するパラメータです。なぜこんなものを導入するのかは、後述します。Batch Normalizationに$x_{i,cxy}$を入力としていれた場合、最終的な出力$y_{i,cxy}$および、正規化した値である$\hat{x_{i,cxy}}$を以下のように定義します。

$$\begin{equation}
\hat{x_{i,cxy}} = \frac{x_{i,cxy} - \mu_{c}}{\sqrt{\sigma_{c}^2 + \epsilon}} \tag{4.3}
\end{equation}$$

$$\begin{equation}
y_{i,cxy} = BN(x_{i,cxy}) = \gamma_{c} \hat{x_{i,cxy}} + \beta_{c} \tag{4.4}
\end{equation}$$

　式(4.3)は式(4.1)、(4.2)を使って、単純に$x_{i,cxy}$を正規化しているのがわかります(分散$\sigma_{c}^2$が0の場合$\hat{x_{i,cxy}}$が無限大になってしまうので、小さな数字$\epsilon$を足しています。Chainerでは$2.0\times 10^{-5}$をデフォルト値として使っています。)。ここで疑問なのが式(4.4)です、ここで$\gamma_{c}$とシフト$\beta_{c}$で線形写像しているのですが、式(4.3)で既に本丸の正規化は終えています、何をしているのでしょうか？
　$\gamma_{c} = \sigma_{c}、\beta_{c}=\mu_{c}$とします。すると$\epsilon$が小さいため無視したとき、$y_{i,cxy}$は以下のようになります。
$$\begin{equation}
y_{i,cxy} = \gamma_{c} \hat{x_{i,cxy}} + \beta_{c} = \sigma_{c} \times \frac{x_{i,cxy} - \mu_{c}}{\sqrt{\sigma_{c}^2}} + \mu_{c} = x_{i,cxy} \tag{4.5}
\end{equation}$$
　式(4.5)を見ると、正規化された$\hat{x_{i,cxy}}$が$\gamma_{c} = \sigma_{c}^2、\beta_{c}=\mu_{c}$によって、元の入力$x_{i,cxy}$に戻されています。これは$\gamma_{c}$とシフト$\beta_{c}$を導入することにより、正規化のため消えてしまう有意な特徴量などを保持することを狙っています。Batch Normlizationで学習されるパラメータはスケール$\gamma_{c}$とシフト$\beta_{c}$のみです。
　　$x_{i,cxy}、\mu_{c}、\sigma_{c}^2、\hat{x_{i,cxy}}、\gamma_{c}、\beta_{c}$はそれぞれ微分可能です。導出は論文内にあります。確認すると確かに微分可能でした。気になる方は、ぜひ導出してみてください。ChainerでBatch Normalizationはワンラインで記述可能です。楽でとてもよいです。

5. Rethinking the Inception Architecture for Computer Vision

　ネットワーク自体はgooglenetを順当に拡張していったものです。この論文の良い所はネットワークの設計方針を言語化したところです。とりわけdownsamplingする前には、ネットワークのチャンネル数を増やすといった部分はとても大切です。

6. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification

　現在のDNNのスタンダードな初期化方法で、xavier初期化をReLU拡張したものです。ReLU初期化、msra初期化、He初期化などと呼ばれたりします。このxavier初期化はforward中に出力の分散値が変わらないような重みの分散を算出する方法で、とても革命的なものです。データdrivenな初期化として、All you need is a good init・Data-dependent Initializations of Convolutional Neural Networksなどが今年提案されたりしましたが、これもxavier初期化を拡張したものです。僕は基本的にmsra初期化で算出した分散値を用いて、対角化したランダム行列を生成し、それらを重みの初期値として使っています。
　この論文では初期化以外にReLUを拡張したPReLUを提案しています。内容は単純で、x<0の部分をReLUのように0にするのでなく、axとするといったものです。このときaを誤差逆伝搬法で学習します。
　この論文の面白い点は学習されたaの値です。以下が結果になります。

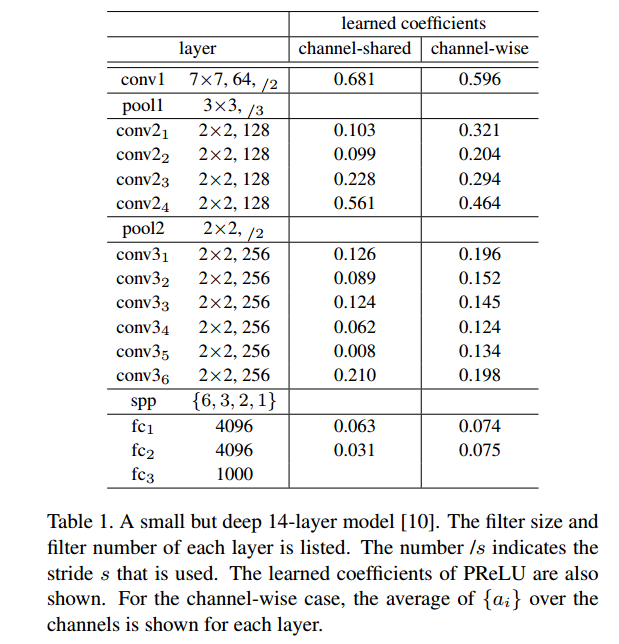
　初期層では大きなaで、上層にいくと小さな値になっていきます。初期層では情報を保持して、上層にいくにつれ情報を捨てていっているように見えます。初期層では線形性を保持し、上層に行くにつれ非線形となっていっているようにも見て取れます。この結果はCReLUと非常に密接しています。CReLUはReLU(x)とReLU(-x)を連結したものを出力するというアイデアの非線形関数です。他にもおもしろい点として、downsampling(pool)する前ではaの値が大きくなる点です。情報がpoolで落ちるので、落とさないようにしているように見えます。
　このaの値を見るとCNNの気持ちがわかるような気がして好きです。

7. Training Very Deep Networks

　Highway networksと呼ばれるものです。Highway networksは数式的に以下のようになります。
$$y=H(x, W_h)T(x, W_T)+xC(x, W_c)$$
$H(x, W_h)$は通常の非線形関数です。$T(x, W_T)$は非線形関数を、$C(x, W_c)$
は入力xをどれだけ荷重するか算出する関数です。$T(x,W_T)=1,C(x,W_c)=1$と単純化したものがResidual Networksになります。そのためResidual NetworksはHighway Networksを単純化したものだ、とよく言われます。論文内では$C(x,W_c)=1-T(x,W_T), 0\le T(x,WT) \le 1$といった形のネットワークを構築しています。
　この論文の面白い点が、学習されたネットワークの上層部分の層を抜いてもネットワークの精度がほとんど変わらないことが観察された点です。実はResidual Networksでも同じ現象が確認されていて、あまりに大量の上層をいじると精度が下がるのですが、数層を抜いたり、シャッフルしたりしても精度がほぼ変わらないことがわかっています[Residual Networks Behave Like Ensembles of Relatively Shallow Networks]。これを知った時は驚きました。

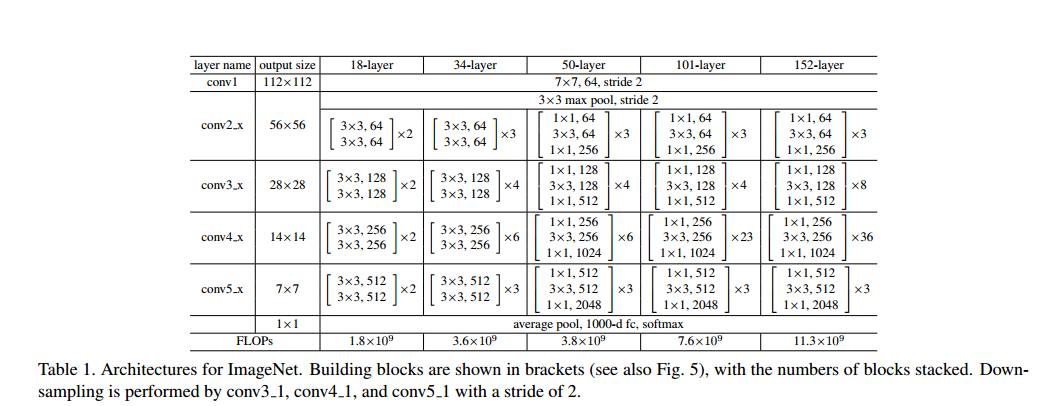
8. Deep Residual Learning for Image Recognition

　認識部門でILSVRC2015の覇者となったネットワークです。Highway Netoworks(7)を単純化した構成になっており、特徴的な部分はresidualと呼ばれ構造になります。今年出たネットワークのほとんどはこれをベースに改良したものになります。

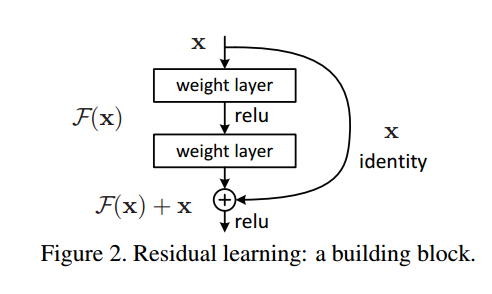
　上図がresidualな構造を端的に示しています。単純に入力xを非線形関数を適用したF(x)に足すだけです。このFを数層のconv、BN、ReLUで構成しています。以下がネットワークの全体図です。

10. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size

　このsqueezenetは非常にコスパが良いモデルです。fire moduleというmoduleが提案されており、それを用いてネットワークが組み上げられています。fire moduleは以下のようになります。

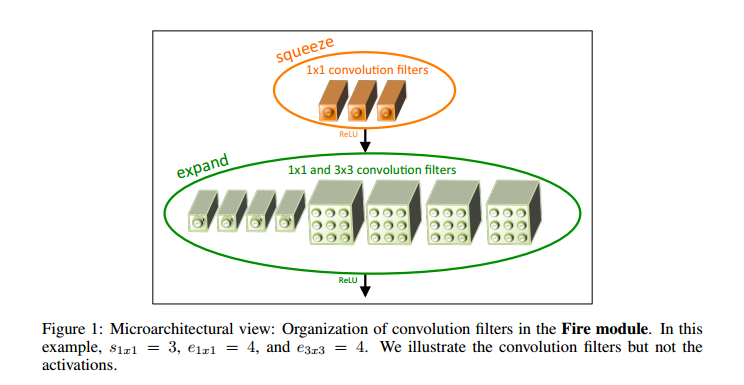
　fire moduleのアイデアは非常に単純で、1x1convで次元削減(次段の入力チャンネル数を減らす)を行った出力を、3x3convと1x1convに入力し、それぞれの出力を連結するといったものです。論文内のネットワークにBNを付与したものは、重み数が0.7M程度でcifar10で92.6%を得ることが出来ます。
　実務で2~100クラスの画像認識タスクを解くなら、これで大体片が付きます。

11. Identity Mappings in Deep Residual Networks

　いくつかの種類のResブロックを試して、BN-ReLU-Conv-BN-ReLU-Convが良かったということが示されている論文です。一般にResidual Networksというと、現在はこれを指すと思います。

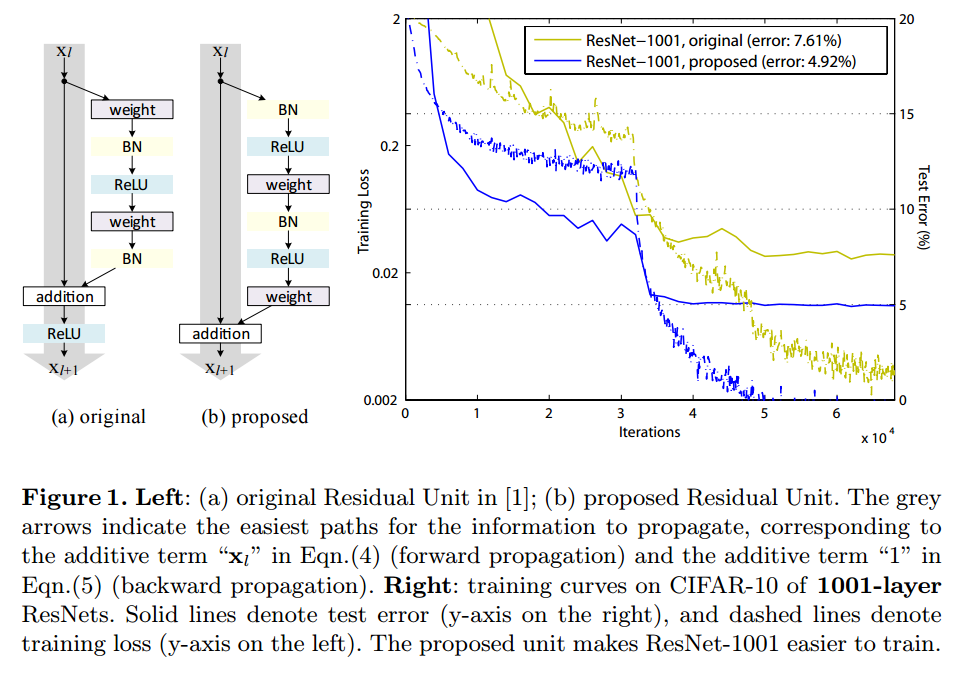
13. Deep Networks with Stochastic Depth

　stochastic depthと呼ばれるもので、確率的にResブロックをdropoutするといった正則化方法です。これは複数の論文のモデルでも既に採用されていて、若干効果が出ているように思えます。しかし24で通常のstochastic depthでは効果がなかったという報告もあるので、stochastic depthに対する評価は暫定的で、注視する必要があります。
　Resブロックに対するdropout確率は、下層から上層に向かって減少させていく手法が、最も精度が出るようです。論文内では、最下層は1(dropをしない)、上層では0.5(50%の確率でdropする)程度のdrop確率を設定し、中間層にはそれら値を線形的に算出したdrop確率を適用する方法が論文内では取られていて、その結果が最も良いです。

14. Swapout: Learning an ensemble of deep architectures

　Resブロックのresidualな部分と非線形関数の出力値それぞれ独立にdropoutをかける手法です。数式で表すと以下のようになります。
$$y=p_{1}F(x)+ p_{2}x$$
$y$はResブロックの出力、$x$は入力、$F$は非線形関数、$p_{1},p_{2}$はベルヌーイ分布で、0か1の出力値を取ります。これはどういうことかというと、以下の図が直感的です。

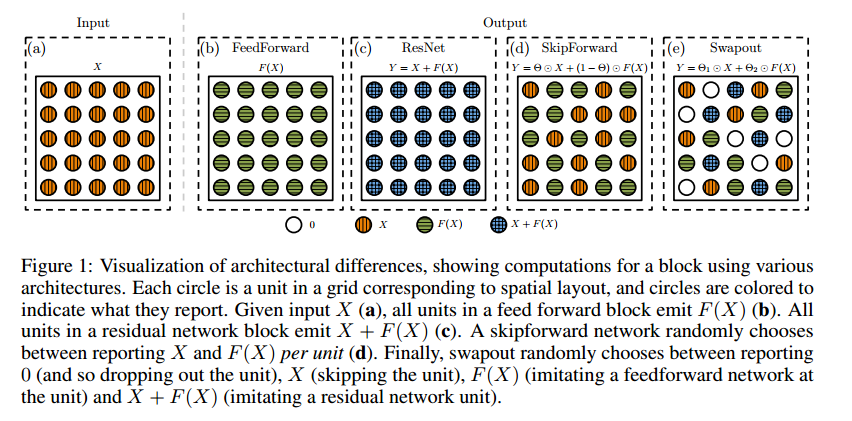
　図のeがswapoutなのですが、見てわかるように出力値が0,x,F(x),F(x)+xのどれかになっているのが見て取れると思います。上式はそれを表しているだけです。swapoutはこれを全てのResブロックに適用したネットワークです。pがTの確率で1、1-Tの確率で0を出力するとしたとき、低層ではTの値を大きく、上層にいくほど小さくするパターンがうまくいっています。

15. Wide Residual Networks

　深くするのでなく、Resブロックの幅を増やしたら、精度が上がるよという論文です。全体のネットワークは以下の図のようになります。

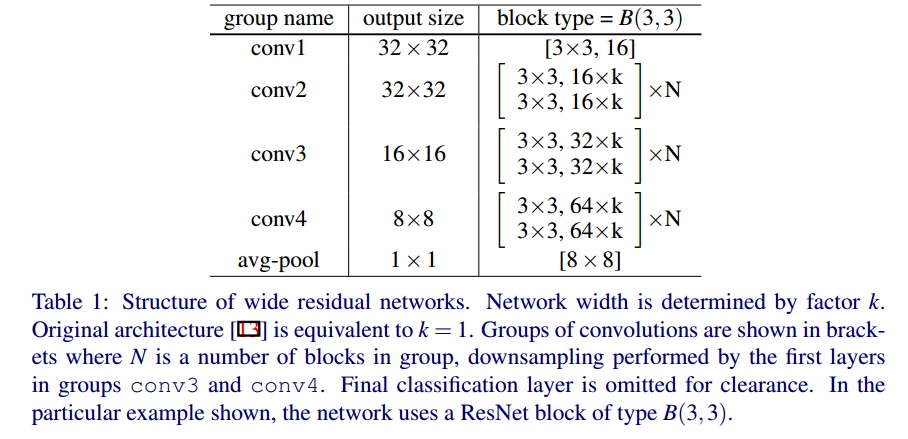
　ブロック数のNと、幅パラメータkでネットワーク構成が決まります。Nを4、kを10としたパターンが論文内で最もうまくいっています。
　もちろんこれだけでは論文にならないので、どのResブロックで精度が出るのかも検証しています。結論として、Resブロック内で3x3のconvを2つ使用するのが良かったことが示されています。3x3convを2つ重ねるのでなく、1、3、4つ重ねたりするケースではパフォーマンスが落ちるといった知見はおもしろかったです。cifar10では効果が出ないのですが、cifar100などのタスクではResブロック内のconv間でdropoutを挿入すると、精度が上がったそうです。
　wideにすると学習速度もはやくなり(Resnet-1001の8倍の学習速度)、通常のResnetと比べて、最大5倍程度のパラメータ数を使用しても学習をすることが可能です。実際に組んだモデルで学習させてみると、学習が本当にはやいです。cifar10では1epoch目で60%程度の精度が出ます。

16. FractalNet: Ultra-Deep Neural Networks without Residuals

　16はfractal netで、residualを持たず、平均値を取る構造とフラクタル的なネットワークであることが特徴的です。平均値を取るため、タイトルにwithout Residualsと付いています。フラクタルな構造は以下の図がわかりやすいです。

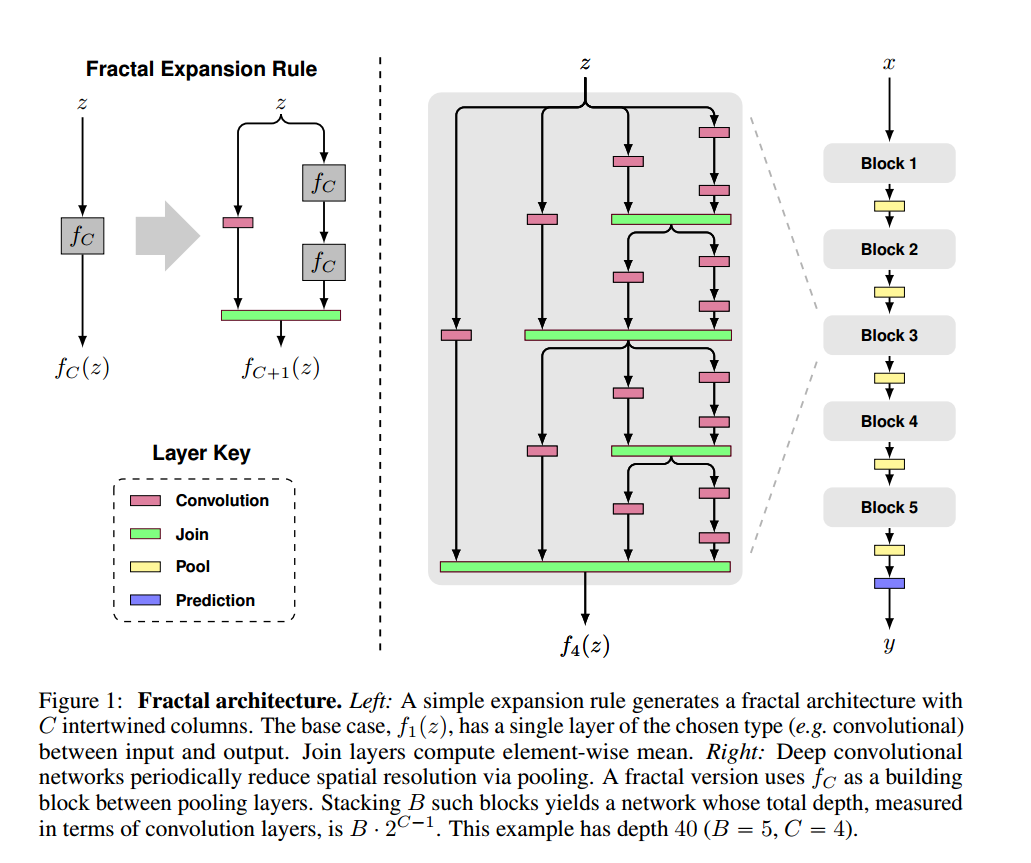
　図にあるようなFractal Expansion Ruleを使ってネットワークを構成します。この論文では2つのconvからの出力に平均値を適用(図のjoin層)しています。joinをresidualした際にネットワークの精度はどうなるか、といったことが非常に興味があります(論文ではjoinに平均のみを適用)。
　論文のタイトルはwithout residualsと謳っていますが、平均を取ることは本質的にresidualと同じであるように感じます。著者は違うと主張しているのですが、個人的には疑問を感じています。
　ネットワークを学習していていておもしろいと思ったのが、最初の20epoch程度は学習が停滞する点です(論文内に記述あり)。あまり見たことがない挙動です。学習係数を大きくしたところ、1epoch目から学習しました(涙目)。

17. Weighted Residuals for Very Deep Networks

　Hを非線形関数、xを入力、$\alpha$を学習パラメータ、yをResブロックの出力とした時、以下の数式のようなResブロックを定義するのが、この論文のメインアイデアです。
$$y=\alpha H(x)+ x$$
　図的には以下のようになります。

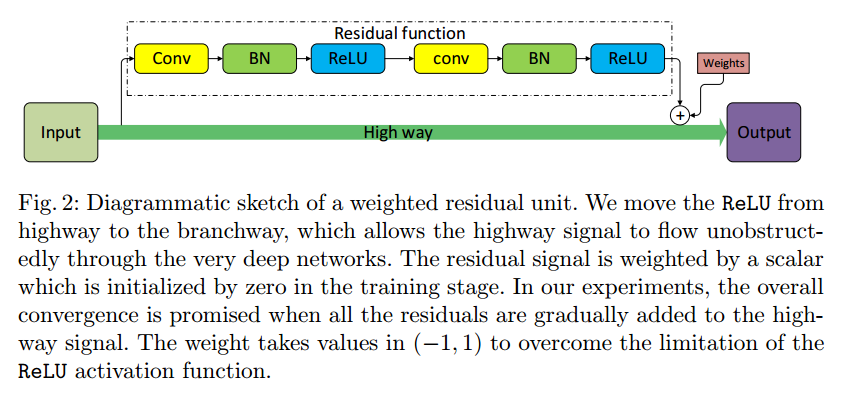
　この論文の面白い点は誤差逆伝搬法で学習される$\alpha$の値です。

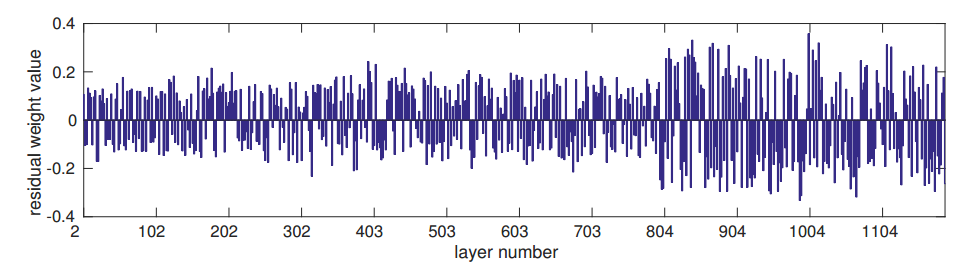
　図を見ると上層では$\alpha$の値が大きい傾向にあるのが見て取れます。H(x)が大きく足されるので、非線形性が上層で積極的に利用されているように見えます。ただH(x)の出力値がとても小さい可能性もあり、その部分の検証は論文内にありません。

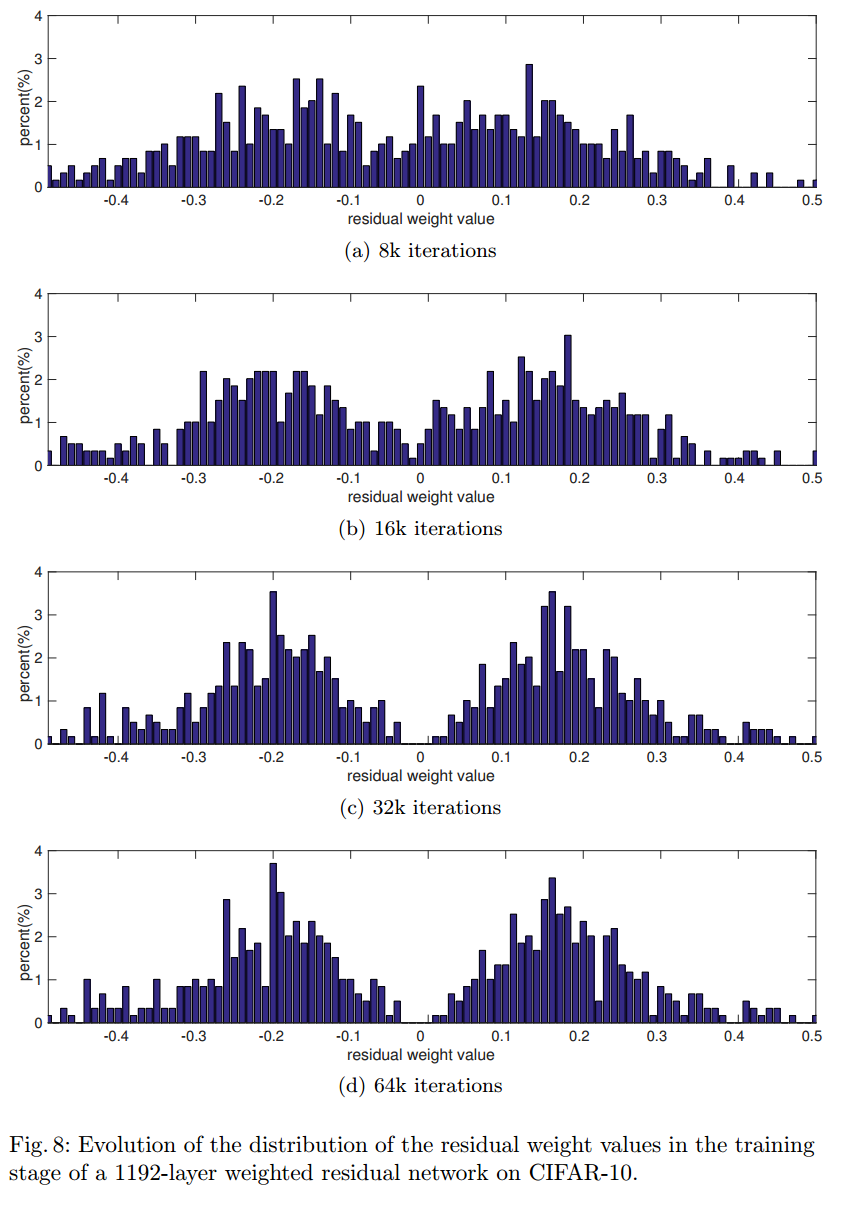
　上図は$\alpha$がどのように変化していったかの図です。おもしろいのが対称性を満たしている点です。何故こうなるのかわかりませんが、とても興味深いです。

18. Residual Networks of Residual Networks: Multilevel Residual Networks

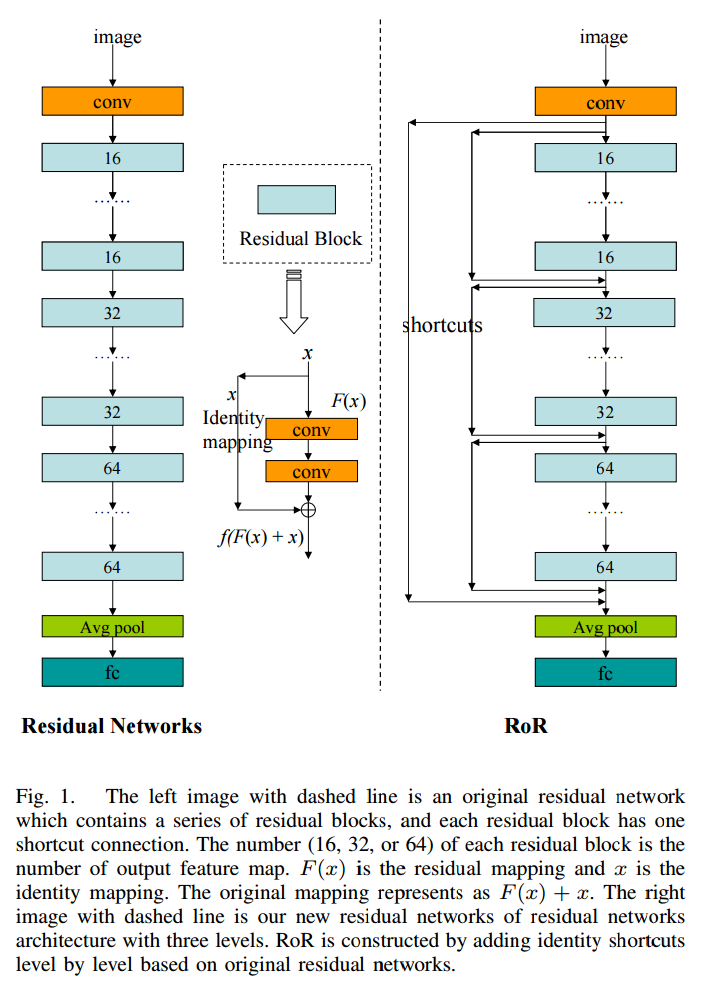
　他のレイヤーからもskip connectionを入れるというシンプルなアイデアです。以下の図を見るのがわかりやすいです。アイデアとしてはこれだけです。

19. Densely Connected Convolutional Networks

　19はDense netで、出力をどんどん入力に連結してブロックに入れていくのが特徴的です。以下の図のように、出力が再帰的に次の入力になっていきます。

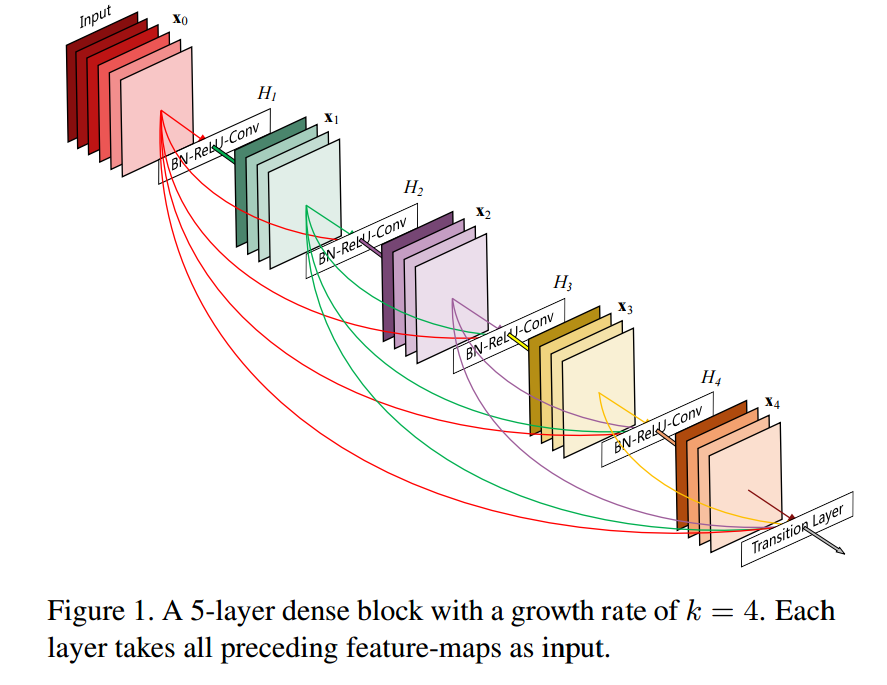
　residualでなく出力を再帰的に連結する点が異なっているのですが、本質的にResidualネットワークと同じことをやっているように思えます。

20. Xception: Deep Learning with Depthwise Separable Convolutions

　Resブロックのconvをseparable convに置き換え、それを用いて構成されたネットワークです。separable convはchannel wiseなconvと1x1convを順に適用したもので、重み数を小さく出来る特徴があります。channel wiseなconvはチャンネル間での相関をみないconvで、畳み込み窓を計算した後に、和を取らずに出力するconvです。
　この論文で主張されているのですが、residual構造がなくても、vggベースのネットワークでinception v4に比類するものが得られることが観察されたそうです。ただしresidual構造を入れたほうが収束がはやいことが、この論文では同時に検証されています。residual構造は黙って入れておけばよいといった感じでしょうか。

21. Deep Pyramidal Residual Networks

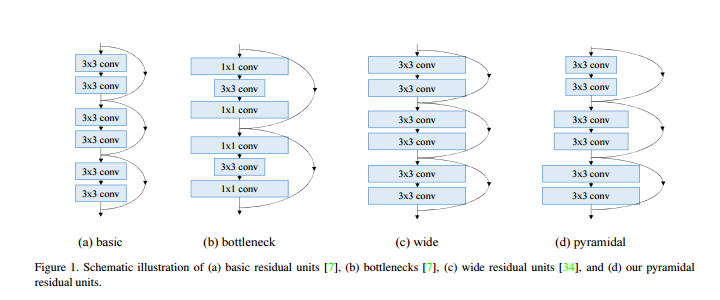
　Resブロックの出力チャンネル数を徐々に大きくしていくというシンプルなアイデアです。一般のResidual NetworksではResブロック内でdownsampleとしてstride2のconvを適用するときに、チャンネル数を事前に2倍にします。pyramidal networksはdownsample前に急激にチャンネル数を増やすのでなく、徐々に増やしていく、図のdのような形のネットワークになります。

22. Neural Architecture Search with Reinforcement Learning

　googleが800個のgpuとRNNを使って、ネットワークの生成をしている論文です。validationデータの精度とpolicy gradientを使って誤差逆伝搬法から適切なCNNネットワークを吐き出すRNNネットワークを学習します。驚く点がcifar10でSoTA程度の精度が出せている点です。
　生成されるネットワークを単純化した点(filterは3,5,7のみなど)と、生成したネットワークの評価をSGDで単純に行う、といった点がうまくいった理由のように思えます。
　生成されたネットワークはとても興味深いです。以下が生成された軽量ネットワークになります。

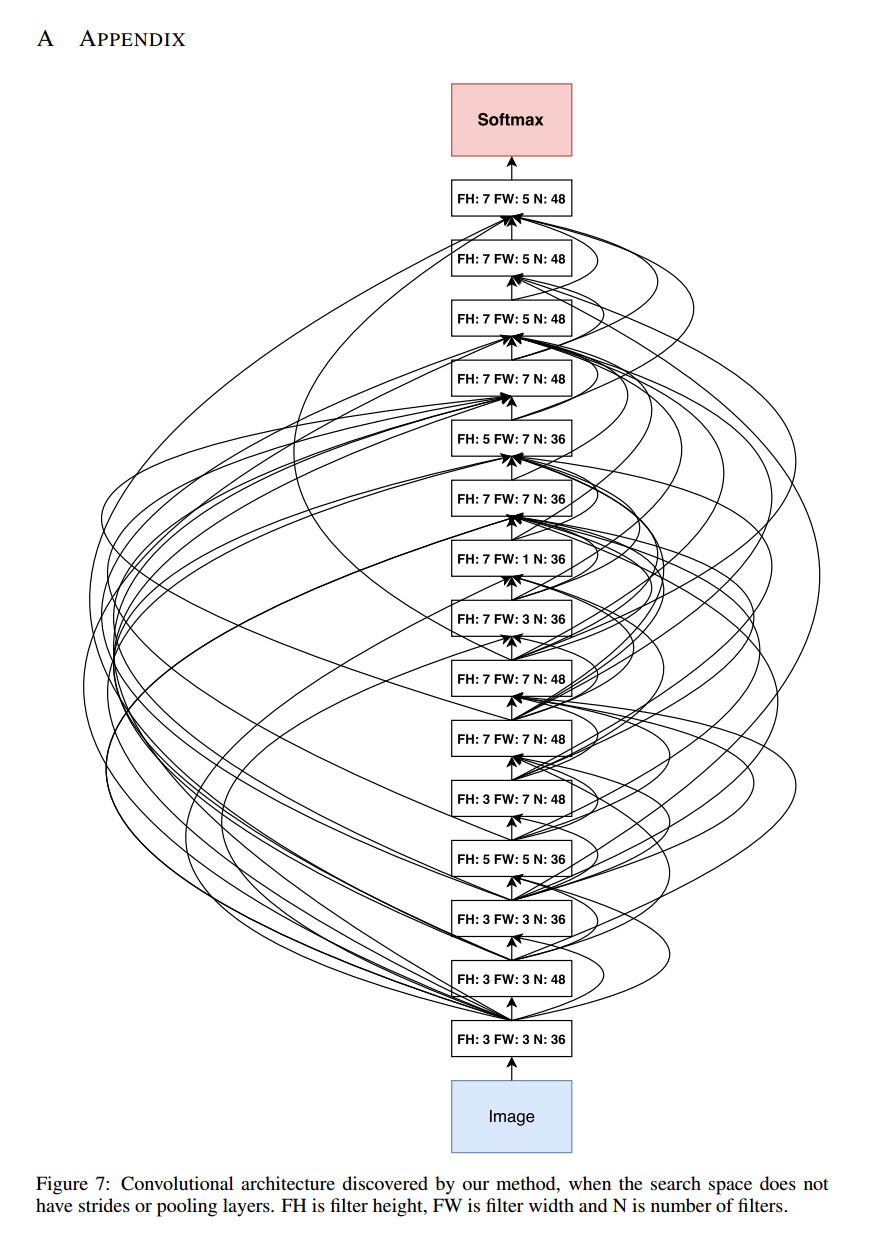
　矢印が合流している点は連結になります。residualな構造はありません。19のdense netと構成が似ています。データがネットワーク構造を決めているので、人間には理解できない非常に複雑な入力になっています。面白い点は、この矢印を削除したり、増やしたりするとテスト精度が下がった点です。
　ネットワーク生成に自由度をもっと与えれば、もっと精度が出るような気がします。しかし自由度が高すぎると、ネットワークが適切に生成できない気がするので、調整作業と実験をするためのハードウェアが必須です。この実験を検証できる環境は、世界でも数えるくらいだと思いますが。。。

23. Aggregated Residual Transformations for Deep Neural Networks

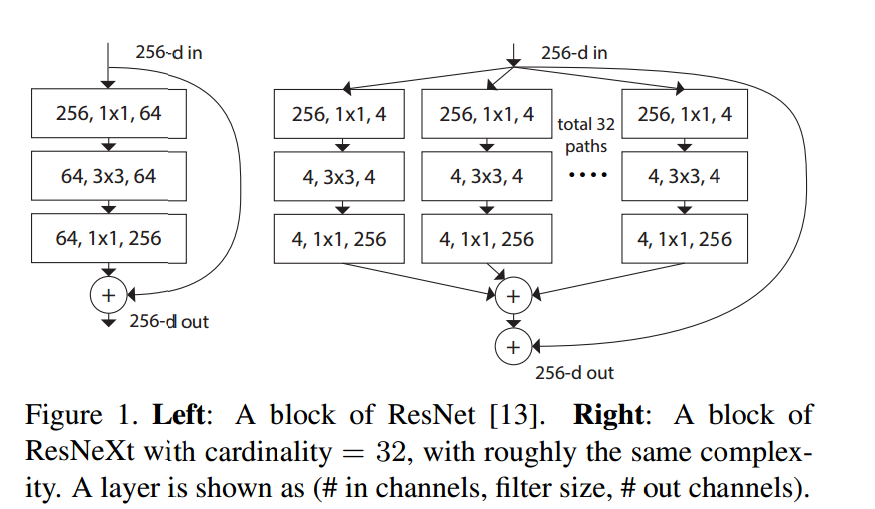
　ResNeXtと呼ばれるネットワークで、上図左にあるようなResブロックを右のようなものと置き換えます。上図右のResブロックは下図の(a),(b),(c)と等価になります。chainerではgroup convがないので、(b)で実装しました。

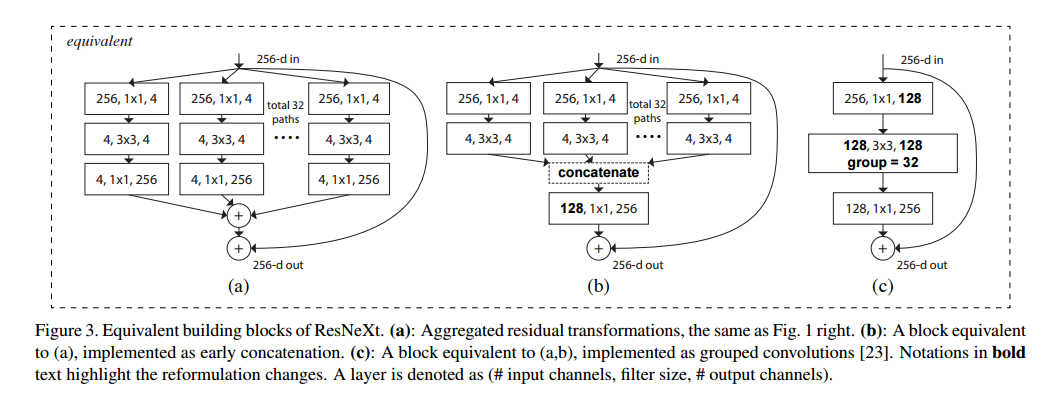
　論文内でResブロック内での入力の分岐数をcardinalityと呼んでいて、cardinalityとブロックの幅を適切に増加させたほうが、単純にブロック幅を増加させた同パラメータ数のWide Residual Networksなどと比べて精度が出ることを主張しています。

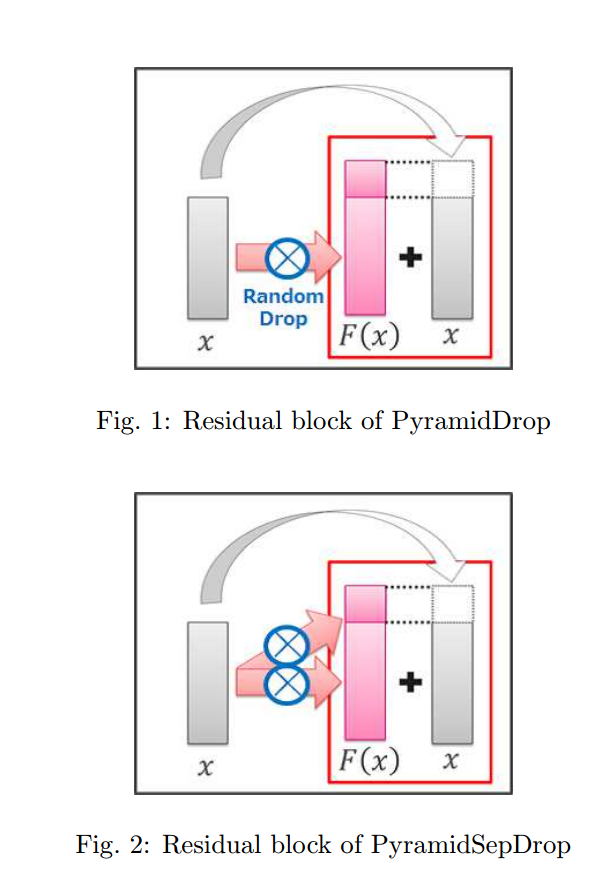
24. Deep Pyramidal Residual Networks with Separated Stochastic Depth

　24は21のpyramidal netにseparated stochastic depthを適用したものになります。separated stochastic depthはチャンネルが増加する部分にもstochastic depthを独立に適用するというアイデアです。以下の図のような形です。

2016年の深層学習を用いた画像認識モデル

最初に

論文

実装