※2023年10月26日：「機械学習としてのカルマンスムーザー」より改題

カルマンフィルター（Kalman Filter）、便利ですよね。
制御工学やロボティクスの世界では割とお馴染みの技術ですが、以前こちらの記事（機械学習としてのカルマンフィルター）がトレンド入りしていたように、機械学習やデータ解析の文脈で語られることは少ないようです。

一方で、制御エンジニアでも カルマンスムーザー（Kalman Smoother） についてはご存じない方が多いんじゃないかと思います。実際、Google検索で「カルマンフィルター」が約120万件ヒットするのに対し、「カルマンスムーザー」が約700件しかヒットしないことが如実に物語っています。（実は他の言い方があるのか？）

名前から想像つくかもしれませんが、カルマンスムーザーはカルマンフィルターを拡張したアルゴリズムです。やや強引ですが、カルマンフィルターが「モデルベース型 オンライン 機械学習」だとすれば、カルマンスムーザーは「モデルベース型 オフライン 機械学習」だといえるかもしれません。

今回は、制御工学では普段あまり扱わない「数理モデル」を題材に、カルマンスムーザーについて紹介したいと思います。

カルマンスムーザーとは

冒頭で、カルマンスムーザーはカルマンフィルターを拡張したアルゴリズムである、と言いました。ここでは両者の違いを少し掘り下げてみます。

カルマンフィルターは、予測と更新という2つのステップを繰り返すことで、ある時点までに得られた誤差を含む情報をもとに、「現在の状態を予測する」アルゴリズムでした。

カルマンフィルターは、その後得られた情報を用いて過去の予測結果を修正することはありません。なので、後から見れば予測結果が明らかに間違っていることもあります。 カルマンフィルターは過去を振り返ることができない のです。オンライン型ゆえに仕方がない面ではあります。

カルマンスムーザーは、カルマンフィルターで得られた予測結果を「遡って修正する」ことができるアルゴリズムです。つまり、 カルマンスムーザーは過去を振り返ることができる といえます。すべての情報が出揃うまで計算に手を付けることはできませんが（＝オフライン型）、データ解析の視点から見れば、実はこちらの方が嬉しいという方も多いのではないでしょうか？

両者の関係を簡単な図に表すとこのようになります。

アルゴリズムの定式化

離散時間モデル

使用する離散時間モデルを以下のように定義します。

\begin{align}
\boldsymbol{x}_t &= f(\boldsymbol{x}_{t-1}, \boldsymbol{u}_t) + \boldsymbol{w}_t \\
\boldsymbol{z}_t &= h(\boldsymbol{x}_t) + \boldsymbol{v}_t
\end{align}

各記号の意味は以下のとおりです。添え字は時刻（ステップ）を表します。

$\boldsymbol{x}$ : 状態ベクトル（推定したい変数）
$\boldsymbol{u}$ : 入力ベクトル
$\boldsymbol{z}$ : 観測ベクトル（誤差を含む）
$\boldsymbol{w}$ : プロセスノイズ（平均$0$・共分散$Q_t$)
$\boldsymbol{v}$ : 観測ノイズ（平均$0$・共分散$R_t$)
$f(\cdot)$ : 状態方程式
$h(\cdot)$ : 観測方程式

今回、$f(\cdot)$と$h(\cdot)$はどちらも非線形関数として定義しているため、カルマンフィルターの計算に直接用いることができません¹。そこで、それぞれの偏微分行列（ヤコビアン）を以下のように定義しておきます。

\begin{align}
F(\bar{\boldsymbol{x}}, \bar{\boldsymbol{u}}) &= \left. \frac{\partial f(\boldsymbol{x}, \boldsymbol{u})}{\partial \boldsymbol{x}} \right|_{\boldsymbol{x}=\bar{\boldsymbol{x}}, \boldsymbol{u}=\bar{\boldsymbol{u}}} \\
H(\bar{\boldsymbol{x}}) &= \left. \frac{\partial h(\boldsymbol{x})}{\partial \boldsymbol{x}} \right|_{\boldsymbol{x}=\bar{\boldsymbol{x}}}
\end{align}

カルマンフィルター

時刻$k$でのカルマンフィルターの予測・更新ステップは以下のように書くことができます。
（ちなみに、具体的な動作原理はこちらの記事が非常によくまとまっています）

予測ステップ （事前推定値・事前誤差共分散）

\begin{align}
\boldsymbol{\hat{x}}_{k|k-1} &= f(\boldsymbol{\hat{x}}_{k-1|k-1}, \boldsymbol{u}_k) \\
P_{k|k-1} &= F(\boldsymbol{x}_{k-1|k-1}, \boldsymbol{u}_k) P_{k-1|k-1}F^T(\boldsymbol{x}_{k-1|k-1}, \boldsymbol{u}_k) + Q_k 
\end{align}

更新ステップ （カルマンゲイン・事後推定値・事後誤差共分散）

\begin{align}
S_k &= H(\boldsymbol{x}_{k|k-1}) P_{k|k-1} H^T(\boldsymbol{x}_{k|k-1}) + R_k \\
K_k &= P_{k|k-1} H^T(\boldsymbol{x}_{k|k-1}) S_k^{-1} \\
\boldsymbol{\hat{x}}_{k|k} &= \boldsymbol{\hat{x}}_{k|k-1} + K_k(\boldsymbol{z}_k - h (\boldsymbol{\hat{x}}_{k|k-1})) \\
P_{k|k} &= (I - K_k H(\boldsymbol{x}_{k|k-1})) P_{k|k-1}  \\
\end{align}

各記号の意味は以下のとおりです。

$\hat{\boldsymbol{x}}_{a|b}$ : 時刻$b$までの情報を考慮に入れた、時刻$a$における$\boldsymbol{x}$の推定値（期待値）
$P_{n|m}$ : $\hat{\boldsymbol{x}}_{a|b}$の誤差共分散（確からしさ）

カルマンスムーザー

スムージングのアルゴリズムは数種類ありますが、今回はRTS（Rauch-Tung-Striebel）と呼ばれるアルゴリズムを使用します。「時刻ステップ（$\Delta t$）が一定であること」という条件付きですが、通常はあまり問題にならないはずです。

時刻$n$まで各時刻の観測量と、カルマンフィルターによる予測結果が得られているとき、各ステップを遡る形で以下の「平滑ステップ」を計算します。

平滑ステップ

\begin{align}
C_k &= P_{k|k} F^T(x_{k+1|n}) P_{k+1|k}^{-1} \\
\hat{\boldsymbol{x}}_{k|n} &= \hat{\boldsymbol{x}}_{k|k} + C_k (\hat{\boldsymbol{x}}_{k+1|n} - \hat{\boldsymbol{x}}_{k+1|k}) \\
P_{k|n} &= P_{k|k} + C_k (P_{k+1|n} - P_{k+1|k}) C_k^T
\end{align}

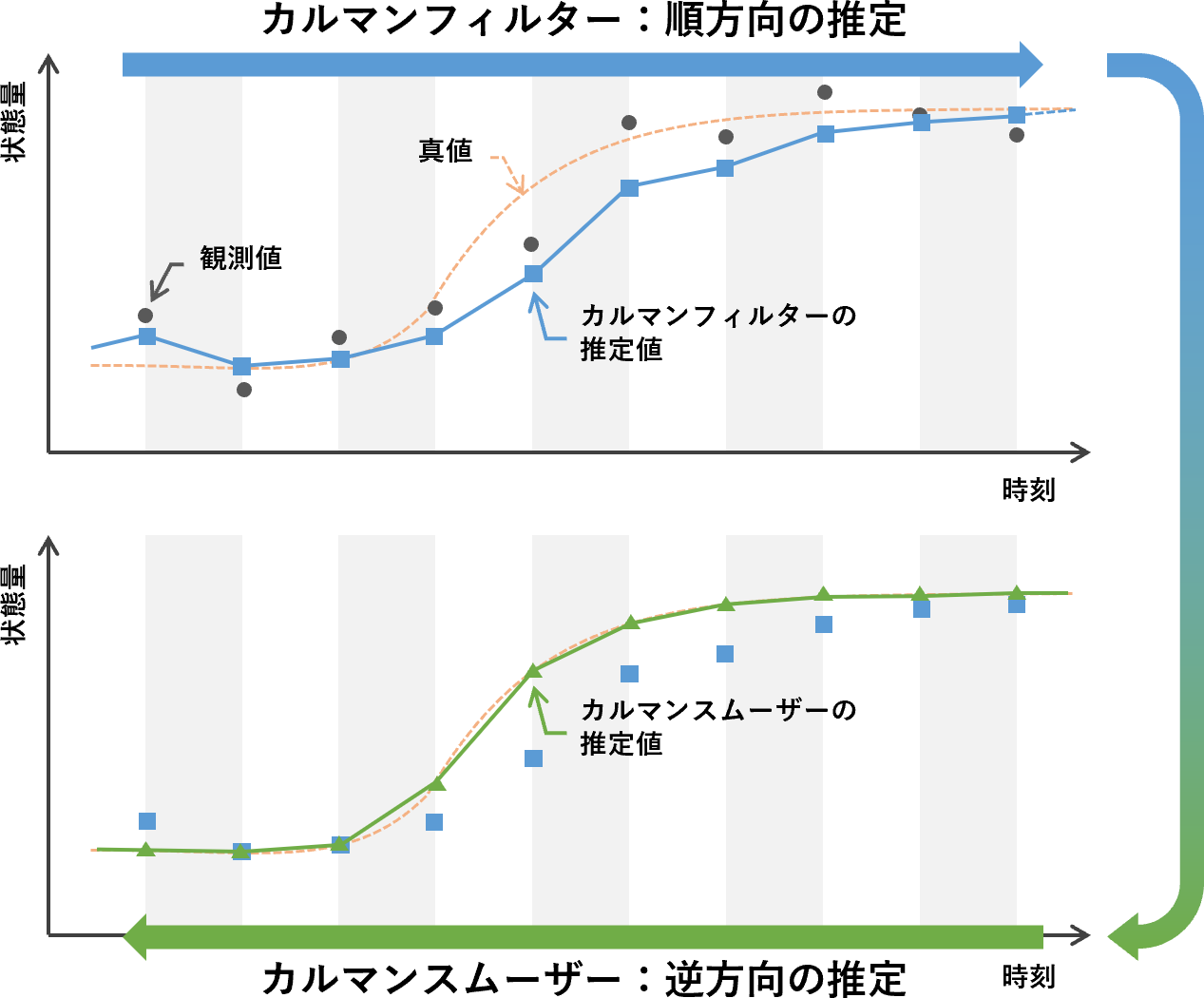
$\hat{\boldsymbol{x}}_{k|n}$という添え字からもわかるように、平滑ステップでは時刻$n$までの情報すべてを使って各時刻の状態を推定しています。情報量について図で表現すると以下のようになるでしょうか。

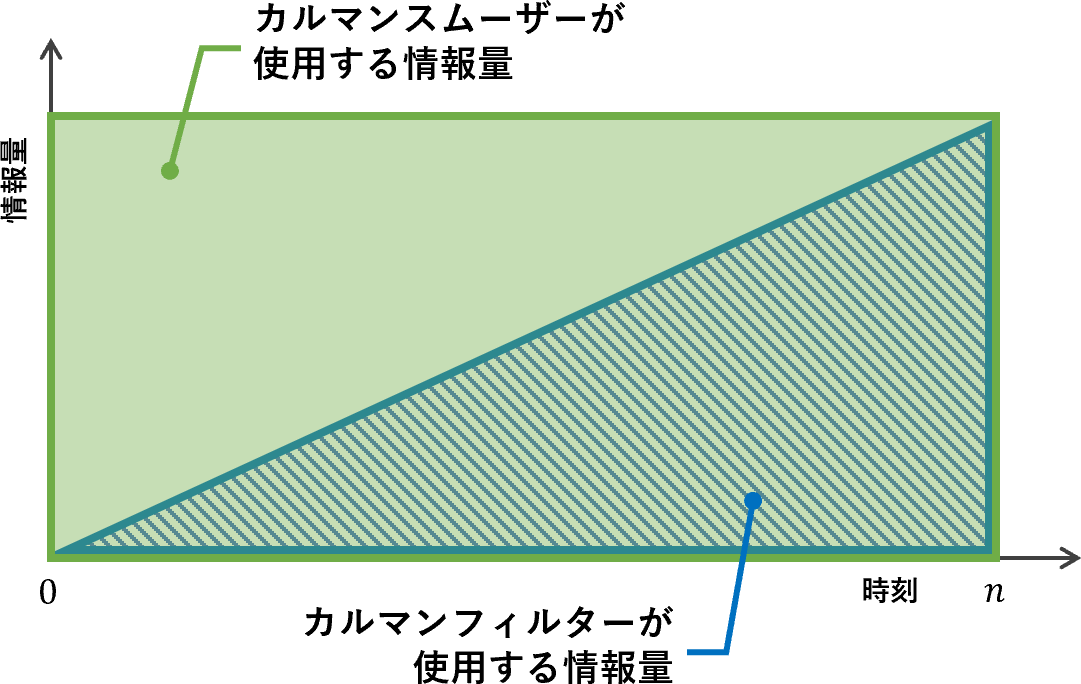
カルマンフィルターが十分な情報量が得られていなかった前半部分では、精度の改善が特に期待できそうです。

問題設定

普段は倒立振子だとかロボットといった「動きモノ」を扱うことがほとんどなのですが、今回はこちらの記事と同じ「（ミジンコの）個体数増加モデル」を取り上げようと思います。連続時間モデルは以下のような非線形微分方程式で表すことができます。

\frac{dn}{dt} = rn \left( 1-\frac{n}{K} \right)

$n$ : 個体数
$r$ : 内的自然増加率（生物固有のパラメータ）
$K$ : 環境収容力（環境依存のパラメータ）

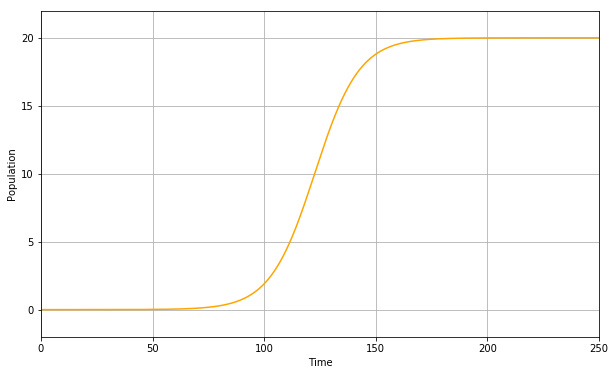
例えば、$r=0.1, K=20$としたときの個体数は以下のグラフのようになります。

今回、$r$は何らかの方法で既に分かっているものと仮定し、個体数の観測値から$n$と$K$を同時に推定することを考えます。ただし、上の式を見ると$K$の逆数が$n$に掛かっています。このままでは非線形性が強く、正しく推定できない可能性があるので、$L=\frac{1}{K}$とおいて$n, L$を推定することにします（それでも非線形であることに変わりはありませんが）。したがって、状態量ベクトルは以下のとおり定義できます。

\boldsymbol{x} = \left[ \begin{matrix} n \\ L \end{matrix} \right]

演算周期を$\Delta t$として微分方程式を離散化すると以下のようになります。なお、今回は途中で個体を追加したり取り出したりすることはないとして、入力$\boldsymbol{u}=0$とします。

\begin{align}
f(\boldsymbol{x}) &= \boldsymbol{x} + \frac{dn}{dt} \Delta t \\
&= \boldsymbol{x}_{t-1} + \left[ \begin{matrix} rn - L n^2 r \\ 0 \end{matrix} \right] \cdot \Delta t \\
\end{align}

h(\boldsymbol{x}) = n

ヤコビアンは以下のように計算できます（$A$は連続時間でのヤコビアンに相当します）。

\begin{align}
F(\bar{\boldsymbol{x}}) &= I + \left[ \begin{matrix} r - 2Lnr & -n^2r \\ 0 & 0 \end{matrix} \right] \Delta t\\
&= I + A \Delta t
\end{align}

H = \left[ \begin{matrix} 1 & 0 \end{matrix} \right]

さて、ここでモデルの可観測性を確認しておきます。「可観測である」とは、簡単にいえば「限られた観測値からすべての状態量を推定できる」ことです。もし可観測ではない場合は、どんなに頑張っても（カルマンフィルターの考え方では）すべての状態量を推定することはできません。

可観測性は、以下のような可観測行列$M_o$の階数（ランク）を計算することで確かめることができます。ここで、$\boldsymbol{x}$の次元を$m$とします（今回の場合は$m=2$です）。$M_o$がフルランクであれば、そのモデルは可観測です。

Mo = \left[ \begin{matrix} C \\ CA \\ \vdots \\ CA^{m-1} \end{matrix} \right]

実際にSymPyを使って計算してみましょう。

from sympy import *

L = Symbol('L')
n = Symbol('n')
r = Symbol('r')

A = Matrix([[r-2*L*n*r, -n*n*r], [0, 0]])
C = Matrix([[1, 0]])

Mo = Matrix([C, C*A])
rank = Mo.rank()

$rank=2$となるので、可観測であることが分かります（ちなみに、$r$も推定しようとすると不可観測になります）。

シミュレーション

実装

必要な式が出揃ったので、Python+Numpyでシミュレーターを実装してみます。基本的には式を書き下していくだけなので、それほど難しくはないはずです（コードは記事の最後に載せてあります）。

パラメータは以下のとおりとしました。

項目	記号	値
シミュレーション時間	$T$	$250$
サンプリング周期	$\Delta t$	$0.1$
内的自然増加率	$r$	$0.1$
環境収容力	$K$	$20$
初期個体数	$n_0$	$0.0001$
プロセスノイズ行列	$Q_t$	$\mathrm{diag}(0, 0)$
観測ノイズ行列	$R_t$	$\mathrm{diag}(\sqrt{2}^2)$
初期値	$\boldsymbol{x}_0$	$\left[ \begin{matrix} n_0 & 1/K \end{matrix} \right]^T$
初期推定値	$\hat{\boldsymbol{x}}_0$	$\left[ \begin{matrix} 0.01 & 0.01 \end{matrix} \right]^T$
初期共分散	$P_0$	$\mathrm{diag}(0.1^2, 0.05^2)$

結果

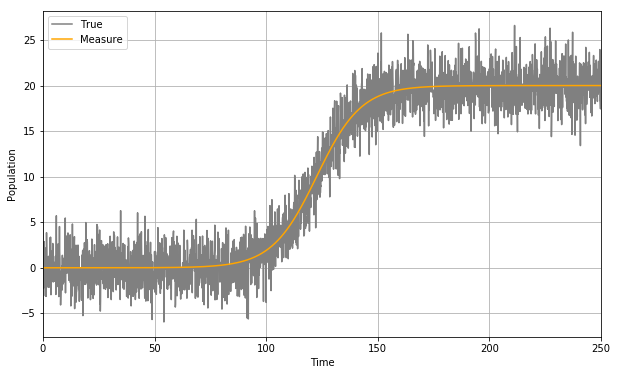
シミュレーション結果を見ていきましょう。まずは個体数（真値）と観測値です。盛大にノイズが乗っていますね。

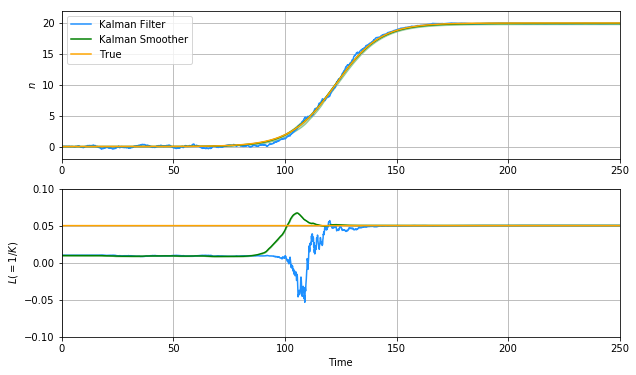
次に、カルマンフィルターによる推定結果を見てみます（網掛けは$P$から求めた推定誤差の$3\sigma$値を示しています）。

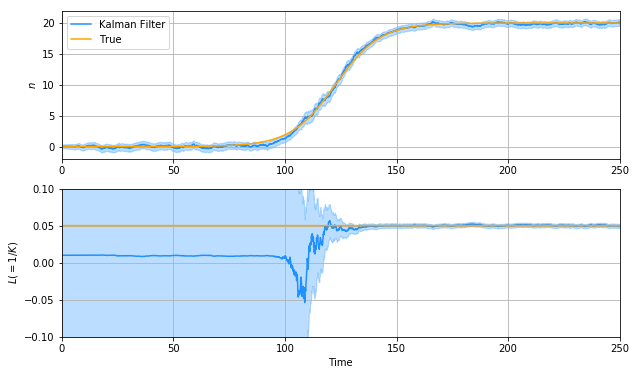
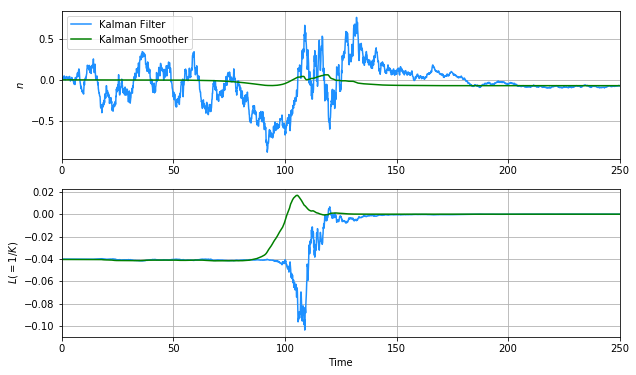
悪くない。そう、正しく実装できていればこの程度にはなるのです。最終的な$L$の推定値は$0.05178$（$K=19.93$）で、環境収容力も1%以下の誤差で推定できていることになります。ただ、$N$の推定値はまだ観測ノイズの影響を受けています。これが事後解析だとしたら、もう少し何とかしたいですよね。

カルマンスムーザーによる推定結果がこちらになります。

拡大してみます。

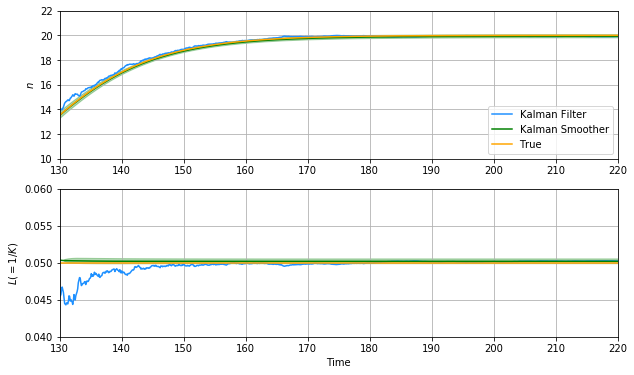
圧倒的ですね。真値とほぼ重なっているといってもいいくらいです。

誤差で比較するとご覧のとおり。

$n$についてはわずかな偏差が残っているものの、目立ったノイズもなく、ほぼ完璧に推定できているといっていいでしょう。これがモデルベース型オフライン機械学習であるカルマンスムーザーの威力です。

ちなみに、前半で$L$が正しく推定できていないのは、 可観測性が悪い ことが原因として考えられます。どういうことでしょうか。

導出した可観測行列$M_o$を改めて確認すると、実はこのような式になっていました。

M_o = \left[ \begin{matrix} 1 & 0 \\ r(1-2np) & -n^2r \end{matrix} \right]

$M_o$がフルランクであるためには、右下の成分$-n^2r$の絶対値がそれなりに大きい必要があります。しかし$n^2$の項を含んでいることから、$n$が小さい場合はほぼ$0$、つまりランク落ち（$\mathrm{rank}(M_o)=1$）してしまいます。そのため、個体数がある程度増えるまではほぼ不可観測の状態となり、$L$の推定が進まないのです。カルマンスムーザーで過去に遡ったとしても可観測性が悪いことに変わりはありませんから、結果はそれほど変化しません（誤差共分散は小さくなってしまってますが）。

一方で、$L$がうまく推定できていない場合でも$n$はよく推定できています。これは直接観測できるからということもありますが、$n$が小さいうちは$L$の影響を受けにくく、$L$が間違っていようと関係ない、というのも大きな理由です。つまり、個体数が少ない場合の増加量は環境収容力によらないということで、モデルの成り立ちから考えても納得がいきます。

なお、この問題はモデルが非線形であることがそもそもの原因です（線形の場合は$M_o$に状態量が含まれない）。より非線形性に強いフィルター（Unscented Kalman Smootherなど）を使えば多少改善するかもしれません。

まとめ

今回はカルマンスムーザーを紹介しました。

カルマンスムーザーがあまりメジャーではない理由として、オフラインでのデータ解析であればもっと優れた手法がたくさんある、というのが実際のところなんじゃないかと思います。とはいえ、カルマンフィルターの延長線上にある技術として割と手軽に使えると思いますし、線形モデルであれば理論的にも最適であることが証明されていますので、これを機にもう少し広まるといいなと思います。

コードは極力シンプルに書いたつもりですので、ぜひ皆さんもこれを参考に、様々な問題に適用してみてください。
ここまでお読みいただきありがとうございました。

ソースコード

import numpy as np
import matplotlib.pyplot as plt

eps = np.finfo(float).eps

## 連続非線形モデル
def f(x, r = 0.1):
    n = x[0]
    L = x[1]

    dx = np.zeros(2)
    dx[0] = r * n - r * n * n * L
    
    return dx

## 離散線形モデル
def A(x, r = 0.1):
    n = x[0]
    L = x[1]
    
    A = np.zeros([2, 2])
    A[0, 0] = r - 2 * n * r * L
    A[0, 1] = - r * n * n
    
    return A

## 初期化
T = 250                             # シミュレーション時間
dt = 0.1                            # 演算周期
meas_step = 1                       # 観測タイミング

nx = 2                              # 状態ベクトルの次元
ny = 1                              # 観測ベクトルの次元

Q = np.diag([0, 0])                 # プロセスノイズ行列
R = np.matrix([2])                  # 観測ノイズ行列
H = np.matrix([1, 0])               # 観測方程式（観測行列）

## シミュレーション
t = np.arange(0, T, dt)             # 時刻ベクトル
N = len(t)

x = np.zeros([N, nx])               # 状態ベクトル（真値）
y = np.zeros([N, ny])               # 観測ベクトル（ノイズなし）
z = np.zeros([N, ny])               # 観測ベクトル（ノイズあり）

np.random.seed(1)
w = np.random.randn(N, nx)          # プロセスノイズ
v = np.random.randn(N, ny)          # 観測ノイズ

x[0,:] = np.array([0.0001, 0.05])   # 初期値

for i in range(1, N):
    x[i,:] = x[i-1,:] + f(x[i-1,:]).dot(dt) + Q.dot(w[i,:])
    y[i,:] = H.dot(x[i,:])
    z[i,:] = y[i,:] + R.dot(v[i,:])

## カルマンフィルター
xp = np.zeros([N, nx])              # 事前推定値（予測ステップの結果）
Pp = np.zeros([N, nx, nx])          # 事前誤差共分散（予測ステップの結果）

xp[0,:] = np.array([0.01, 0.01])        # 初期推定値
Pp[0,:,:] = np.diag([0.1**2, 0.05**2])  # 初期共分散

xu = np.copy(xp)                    # 事後推定値（更新ステップの結果）
Pu = np.copy(Pp)                    # 事後誤差共分散（更新ステップの結果）

for i in range(1, N):
    # 予測ステップ
    xp[i,:] = xu[i-1,:] + f(xu[i-1,:]).dot(dt)

    F = np.eye(nx) + A(xu[i-1,:]).dot(dt)
    Pp[i,:,:] = F.dot(Pu[i-1,:,:]).dot(F.T) + Q
    
    # 更新ステップ
    if i % meas_step == 0:
        e = z[i,:] - H.dot(xp[i,:])
        S = R + H.dot(Pp[i,:,:]).dot(H.T)
        K = Pp[i,:,:].dot(H.T).dot(np.linalg.inv(S))
        xu[i,:] = xp[i,:] + K.dot(e).squeeze()
        Pu[i,:,:] = (np.eye(nx) - K.dot(H)).dot(Pp[i,:,:])
    else:
        xu[i,:] = xp[i,:]
        Pu[i,:,:] = Pp[i,:,:]
       
## カルマンスムーザー
xs = np.zeros([N, nx])              # 推定値
Ps = np.zeros([N, nx, nx])          # 誤差共分散
xs[-1,:] = xu[-1,:]
Ps[-1,:,:] = Pu[-1,:,:]

for i in reversed(range(N-1)):
    # 平滑ステップ
    F = np.eye(nx) + A(xs[i+1,:]).dot(dt)
    C = Pu[i,:,:].dot(F.T).dot(np.linalg.inv(Pp[i+1,:,:]))
    
    xs[i,:] = xu[i,:] + C.dot(xs[i+1,:] - xp[i+1,:]).squeeze()
    Ps[i,:,:] = Pu[i,:,:] + C.dot(Ps[i+1,:,:] - Pp[i+1,:,:]).dot(C.T)

## 誤差共分散から標準偏差σを計算
pdf = np.zeros([N, nx])
pds = np.zeros([N, nx])

for i in range(nx):
    pdf[:,i] = np.sqrt(np.maximum(Pu[:,i,i], eps))
    pds[:,i] = np.sqrt(np.maximum(Ps[:,i,i], eps))


## プロット
plt.close('all')

# 観測値
plt.figure()
plt.plot(t, z[:,0], 'grey', t, x[:,0], 'orange')
plt.grid()
plt.xlim([0,T])
plt.xlabel('Time')
plt.ylabel('Population')
plt.legend(['True', 'Measure'], loc='upper left')

# カルマンフィルターの演算結果
plt.figure()
plt.subplot(2,1,1)
plt.fill_between(t, xp[:,0] - pdf[:,0] * 3, xp[:,0] + pdf[:,0] * 3, alpha = 0.3, color = 'dodgerblue')
plt.plot(t, xp[:,0], 'dodgerblue', t, x[:,0], 'orange')
plt.grid()
plt.xlim([0,T])
plt.ylim([-2,22])
plt.ylabel('$n$')
plt.legend(['Kalman Filter', 'True'], loc='upper left')

plt.subplot(2,1,2)
plt.fill_between(t, xp[:,1] - pdf[:,1] * 3, xp[:,1] + pdf[:,1] * 3, alpha = 0.3, color = 'dodgerblue')
plt.plot(t, xp[:,1], 'dodgerblue', t, x[:,1], 'orange')
plt.grid()
plt.xlim([0,T])
plt.ylim([-0.1, 0.1])
plt.xlabel('Time')
plt.ylabel('$L(=1/K)$')

# カルマンスムーザーの演算結果
plt.figure()
plt.subplot(2,1,1)
plt.fill_between(t, xs[:,0] - pds[:,0] * 3, xs[:,0] + pds[:,0] * 3, alpha = 0.3, color = 'green')
plt.plot(t, xp[:,0], 'dodgerblue', t, xs[:,0], 'green', t, x[:,0], 'orange')
plt.grid()
plt.xlim([0,T])
plt.ylim([-2,22])
plt.ylabel('$n$')
plt.legend(['Kalman Filter', 'Kalman Smoother', 'True'], loc='lower right')

plt.subplot(2,1,2)
plt.fill_between(t, xs[:,1] - pds[:,1] * 3, xs[:,1] + pds[:,1] * 3, alpha = 0.3, color = 'green')
plt.plot(t, xp[:,1], 'dodgerblue', t, xs[:,1], 'green', t, x[:,1], 'orange')
plt.grid()
plt.xlim([0,T])
plt.ylim([-0.1, 0.1])
plt.xlabel('Time')
plt.ylabel('$L(=1/K)$')

# 誤差
plt.figure()
plt.subplot(2,1,1)
plt.plot(t, xp[:,0] - x[:,0], 'dodgerblue', t, xs[:,0] - x[:,0], 'green')
plt.grid()
plt.xlim([0,T])
plt.ylabel('$n$')
plt.legend(['Kalman Filter', 'Kalman Smoother'], loc='upper left')

plt.subplot(2,1,2)
plt.plot(t, xp[:,1] - x[:,1], 'dodgerblue', t, xs[:,1] - x[:,1], 'green')
plt.grid()
plt.xlim([0,T])
plt.xlabel('Time')
plt.ylabel('$L(=1/K)$')

つまり、実際に定義しているのは「拡張カルマンフィルター（Extended Kalman Filter）」「拡張カルマンスムーザー（Extended Kalman Smoother）」ということになります。 ↩

ざっくり解説！カルマンスムーザー（サンプルコード付き）