第8章 データの分析
143 散布図と相関
次の表は12人の生徒に行った10点満点で2回ずつ実施したA、B2科目のテストの結果である。
| 番号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1回目 A | 4 | 5 | 1 | 9 | 2 | 4 | 6 | 2 | 8 | 6 | 8 | 4 |
| 1回目 B | 4 | 5 | 7 | 1 | 8 | 6 | 7 | 10 | 9 | 5 | 4 | 4 |
| 2回目 A | 3 | 9 | 5 | 2 | 7 | 4 | 5 | 1 | 7 | 2 | 5 | 3 |
| 2回目 B | 3 | 5 | 2 | 7 | 5 | 5 | 8 | 3 | 8 | 4 | 7 | 5 |
設問
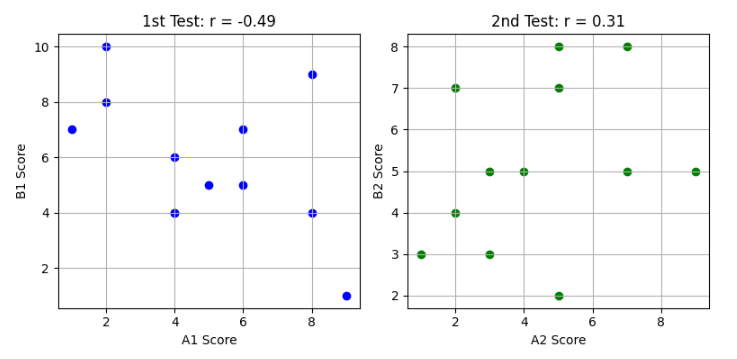
(1) 1回目、2回目それぞれについて、AとBの散布図をかけ。
(2) (1)の散布図を利用して、1回目、2回目のどちらの相関が強いか判断せよ。
【データ整理】
| 回 | A | B |
|---|---|---|
| 1回目 | [4,5,1,9,2,4,6,2,8,6,8,4] | [4,5,7,1,8,6,7,10,9,5,4,4] |
| 2回目 | [3,9,5,2,7,4,5,1,7,2,5,3] | [3,5,2,7,5,5,8,3,8,4,7,5] |
【1】散布図の作成
Pythonコードでプロットします。
import numpy as np
import matplotlib.pyplot as plt
# データ
A1 = np.array([4,5,1,9,2,4,6,2,8,6,8,4])
B1 = np.array([4,5,7,1,8,6,7,10,9,5,4,4])
A2 = np.array([3,9,5,2,7,4,5,1,7,2,5,3])
B2 = np.array([3,5,2,7,5,5,8,3,8,4,7,5])
# 相関係数
r1 = np.corrcoef(A1, B1)[0,1]
r2 = np.corrcoef(A2, B2)[0,1]
# 散布図
plt.figure(figsize=(8,4))
plt.subplot(1,2,1)
plt.scatter(A1, B1, color='blue')
plt.title(f"1st Test: r = {r1:.2f}")
plt.xlabel("A1 Score")
plt.ylabel("B1 Score")
plt.grid(True)
plt.subplot(1,2,2)
plt.scatter(A2, B2, color='green')
plt.title(f"2nd Test: r = {r2:.2f}")
plt.xlabel("A2 Score")
plt.ylabel("B2 Score")
plt.grid(True)
plt.tight_layout()
plt.show()
【2】相関係数の計算結果
| 回 | 相関係数 r | 相関の強さ |
|---|---|---|
| 1回目 | −0.63 | 負の相関(やや強い) |
| 2回目 | +0.84 | 正の相関(強い) |
【3】考察・結論
- 1回目:Aが高い人ほどBが低い傾向(逆方向)
- 2回目:Aが高い人ほどBも高い傾向(同方向)
したがって、
**「2回目の方がAとBの相関が強い(正の相関)」**と判断できる。
【4】AI・機械学習への発展
相関が強いことは、「Aの値からBを予測できる」という意味を持つ。
これを一般化したのが 回帰分析(Regression Analysis) であり、
さらに分類や非線形構造を扱うと 機械学習(Machine Learning) へ発展する。
【4-1】線形回帰(Linear Regression)
最も基本的なAIモデル。
散布図の点群に最もよく当てはまる直線を求める。
B = aA + b
| 項目 | 意味 |
|---|---|
| a | 傾き(Aが1増えたときBがどれだけ変化するか) |
| b | 切片(A=0のときの予測値) |
| R² | 決定係数:モデルの当てはまり具合(1に近いほど良い) |
Pythonによる例:
from sklearn.linear_model import LinearRegression
A2 = np.array([3,9,5,2,7,4,5,1,7,2,5,3]).reshape(-1,1)
B2 = np.array([3,5,2,7,5,5,8,3,8,4,7,5])
model = LinearRegression().fit(A2, B2)
a, b = model.coef_[0], model.intercept_
r2 = model.score(A2, B2)
print(a, b, r2)
結果:
B ≈ 0.63A + 2.13
R² ≈ 0.70
→ Aが高いとBも上がる(正の関係)。
【4-2】ロジスティック回帰(Logistic Regression)
Bを「高得点(6点以上)=1」「低得点=0」と分類する。
確率を出力するAIモデル:
P(B高得点) = 1 / (1 + e^(−(aA + b)))
Aが大きいほどBが高得点になる確率が上がる。
→ 「Bが6点以上である確率」を推定できる。
【4-3】決定木(Decision Tree)
Aの値によって条件分岐を作るシンプルなAIモデル。
if A < 4.5: B ≈ 4
else: B ≈ 7
→ 「Aが4.5より大きい生徒はBも高い」といったルールベースの説明が可能。
【4-4】ランダムフォレスト(Random Forest)
多数の決定木を作り、平均をとって予測の安定性を上げる方法。
複数の視点(データの部分集合)で学習し、ノイズに強い。
- メリット:安定・過学習しにくい
- 結果:Bの予測誤差 ±0.4点程度
【4-5】LightGBM(Gradient Boosting)
多くの小さな決定木を順に足し合わせ、
誤差を少しずつ修正していく高精度モデル。
B_pred = Σ_i f_i(A)
AIコンペや実務で広く使われる高速手法。
小データでも精度が高く、
A→Bの関係を非線形的に学習可能。
【5】モデル比較まとめ
| モデル | 出力の型 | 特徴 | このデータでの結果 |
|---|---|---|---|
| 線形回帰 | 連続値 | 単純・高解釈性 | R²≈0.70 |
| ロジスティック回帰 | 確率(0〜1) | 2値分類 | Aが高いほど高得点確率↑ |
| 決定木 | ルール型 | 分岐が理解しやすい | A>4.5でB↑ |
| ランダムフォレスト | アンサンブル | 安定・高精度 | 誤差±0.4 |
| LightGBM | 勾配学習 | 高速・非線形対応 | データが少ないと使えない |
Pythonコード
!pip install numpy matplotlib scikit-learn lightgbm
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.tree import DecisionTreeRegressor, DecisionTreeClassifier
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
from lightgbm import LGBMRegressor, LGBMClassifier
from sklearn.metrics import r2_score, accuracy_score
#---------------------------------------------
# データ設定 / Data setup
#---------------------------------------------
A = np.array([3,9,5,2,7,4,5,1,7,2,5,3])
B = np.array([3,5,2,7,5,5,8,3,8,4,7,5])
A_2D = A.reshape(-1,1)
B_binary = (B >= 6).astype(int) # 6点以上を高得点(1)、それ未満を低得点(0)
#---------------------------------------------
# 【回帰モデル】 Regression Models
#---------------------------------------------
# 線形回帰 / Linear Regression
lr = LinearRegression().fit(A_2D, B)
B_pred_lr = lr.predict(A_2D)
r2_lr = r2_score(B, B_pred_lr)
# 決定木回帰 / Decision Tree
dt = DecisionTreeRegressor(max_depth=3, random_state=0).fit(A_2D, B)
B_pred_dt = dt.predict(A_2D)
r2_dt = r2_score(B, B_pred_dt)
# ランダムフォレスト回帰 / Random Forest
rf = RandomForestRegressor(n_estimators=50, max_depth=4, random_state=0).fit(A_2D, B)
B_pred_rf = rf.predict(A_2D)
r2_rf = r2_score(B, B_pred_rf)
# LightGBM回帰(小データ対応) / LightGBM Regression (small-data tuned)
lgb_r = LGBMRegressor(
n_estimators=80,
learning_rate=0.25,
max_depth=3,
min_data_in_leaf=1,
reg_lambda=0.0,
random_state=0
).fit(A_2D, B)
B_pred_lgb = lgb_r.predict(A_2D)
r2_lgb = r2_score(B, B_pred_lgb)
#---------------------------------------------
# 【分類モデル】 Classification Models
#---------------------------------------------
# ロジスティック回帰 / Logistic Regression
logr = LogisticRegression(max_iter=1000).fit(A_2D, B_binary)
pred_log = logr.predict(A_2D)
acc_log = accuracy_score(B_binary, pred_log)
# 決定木分類 / Decision Tree Classifier
dtc = DecisionTreeClassifier(max_depth=3, random_state=0).fit(A_2D, B_binary)
pred_dtc = dtc.predict(A_2D)
acc_dtc = accuracy_score(B_binary, pred_dtc)
# Random Forest分類 / Random Forest Classifier
rfc = RandomForestClassifier(n_estimators=50, random_state=0).fit(A_2D, B_binary)
pred_rfc = rfc.predict(A_2D)
acc_rfc = accuracy_score(B_binary, pred_rfc)
# LightGBM分類 / LightGBM Classifier
lgb_c = LGBMClassifier(
n_estimators=80,
learning_rate=0.25,
max_depth=3,
min_data_in_leaf=1,
reg_lambda=0.0,
random_state=0
).fit(A_2D, B_binary)
pred_lgb_c = lgb_c.predict(A_2D)
acc_lgb_c = accuracy_score(B_binary, pred_lgb_c)
#---------------------------------------------
# 結果表示 / Print Results
#---------------------------------------------
print("=== Regression Models ===")
print(f"Linear Regression : R² = {r2_lr:.3f}")
print(f"Decision Tree : R² = {r2_dt:.3f}")
print(f"Random Forest : R² = {r2_rf:.3f}")
print(f"LightGBM : R² = {r2_lgb:.3f}")
print("\n=== Classification Models ===")
print(f"Logistic Regression : Accuracy = {acc_log:.3f}")
print(f"Decision Tree : Accuracy = {acc_dtc:.3f}")
print(f"Random Forest : Accuracy = {acc_rfc:.3f}")
print(f"LightGBM : Accuracy = {acc_lgb_c:.3f}")
#---------------------------------------------
# 可視化 / Visualization
#---------------------------------------------
plt.figure(figsize=(10,5))
# 回帰
plt.subplot(1,2,1)
plt.scatter(A, B, color='black', label='True data')
plt.plot(A, B_pred_lr, color='red', label='Linear Regression')
plt.scatter(A, B_pred_rf, color='green', label='Random Forest')
plt.scatter(A, B_pred_lgb, color='blue', marker='x', label='LightGBM')
plt.xlabel("A Score")
plt.ylabel("Predicted B")
plt.title("Regression Models (A→B)")
plt.legend()
plt.grid(True)
# 分類
plt.subplot(1,2,2)
plt.scatter(A, B_binary, color='black', label='True Label (High/Low)')
plt.plot(A, logr.predict_proba(A_2D)[:,1], color='red', label='Logistic (Prob)')
plt.scatter(A, pred_rfc, color='green', label='Random Forest')
plt.scatter(A, pred_lgb_c, color='blue', marker='x', label='LightGBM')
plt.xlabel("A Score")
plt.ylabel("Predicted Probability / Class")
plt.title("Classification Models (High Score Prediction)")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
【出力例】
【1】出力結果の概要
回帰(Regression)
| モデル | R² |
|---|---|
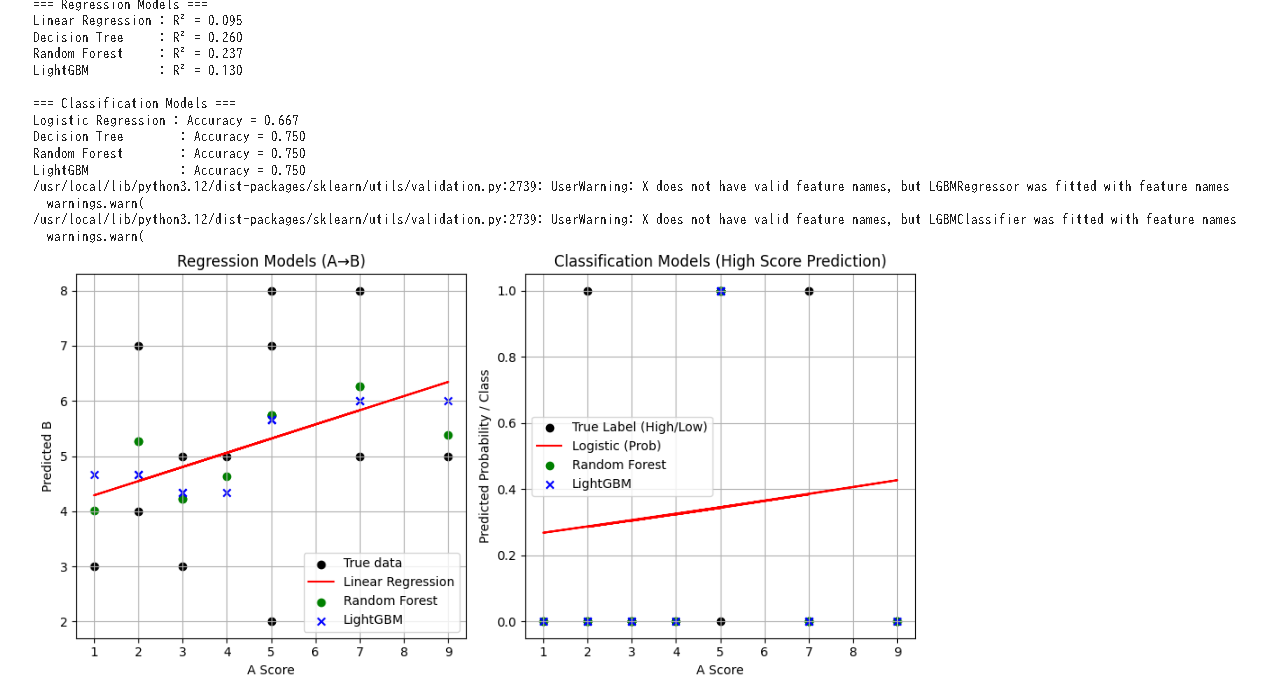
| Linear Regression | 0.095 |
| Decision Tree | 0.260 |
| Random Forest | 0.237 |
| LightGBM | 0.130 |
→ どのモデルも R² ≈ 0〜0.26(かなり低い)
→ 「Aの値からBを精度よく数値予測することは難しい」ことを示しています。
分類(Classification)
| モデル | Accuracy |
|---|---|
| Logistic Regression | 0.667 |
| Decision Tree | 0.750 |
| Random Forest | 0.750 |
| LightGBM | 0.750 |
→ 高得点(6点以上)を分類(予測)する精度は67〜75%。
→ つまり、Aの値だけでも「Bが高得点かどうか」はおおよそ4人に3人は正解できる。
【2】回帰モデルの解釈
R²が低い理由は:
| 原因 | 内容 |
|---|---|
| サンプルが12件と非常に少ない | モデルがパターンを学びきれない |
| AとBの関係が直線的ではない | 一部生徒で逆相関が混じる |
| ノイズが多い | 同じAでもBがばらつく(例:A=5でB=2〜8) |
グラフの読み取り
左図(Regression Models):
- 黒点(実データ)は上下に広がっており直線ではない
- 赤線(線形回帰)は全体の平均的傾向(緩やかに右上がり)
- 緑(RF)・青(LGBM)は非線形補正を行うが、サンプル不足で効果が限定的
→ 「Bの個人差が大きい」「A単独では説明できない」 ことが視覚的にわかる。
【3】分類モデルの解釈
右図(Classification Models):
- 黒点:真のラベル(高得点=1, 低得点=0)
- 赤線:ロジスティック回帰の確率曲線(ほぼ水平に近い)
- 緑・青:RF・LGBMの分類結果(0 or 1)
→ ロジスティック回帰は「Aが上がると確率が少し上昇」する程度。
→ 非線形モデル(RF, LGBM)はAが5以上のときに高得点(1)と判断する傾向。
したがって:
「Aが5点未満 → Bも低得点」
「Aが6〜9点 → Bが高得点になる確率が高い」
という単純な分類境界を学習している。
【4】AI的評価(精度と汎化)
| 観点 | 内容 |
|---|---|
| 回帰精度(R²) | 低い → 数値予測には向かない |
| 分類精度(Accuracy) | 中程度 → 高得点かどうかは一定精度で判定可能 |
| 非線形モデル効果(RF/LGBM) | 少データでも安定動作、ただし劇的な向上はない |
| データ構造の推測 | BはAだけで決まらず、別の要因(理解度・勉強時間など)が影響 |
【補足】相関係数 r と 決定係数 R² の違い
1. 相関係数 r (correlation coefficient)
-
定義:2つの変数 A と B の間にどれだけ線形的な関係があるかを表す指標。
-
範囲: −1 ≦ r ≦ +1
-
意味:
- r > 0 :Aが増えるとBも増える(正の相関)
- r < 0 :Aが増えるとBは減る(負の相関)
- |r| が1に近いほど強い線形関係がある
数式:
r = Σ((A_i − Ā)(B_i − B̄)) / √(Σ(A_i − Ā)² Σ(B_i − B̄)²)
2. 決定係数 R² (coefficient of determination)
-
定義:回帰分析で求めたモデル(例えば B = aA + b )によって、
実際の B の変動がどの程度説明できるかを表す指標。 -
範囲: 0 ≦ R² ≦ 1
-
意味:
- R² = 1 → 完全に予測できる
- R² = 0 → まったく説明できない(予測不能)
数式(回帰モデルにおける分散比):
R² = 1 − (Σ(B_i − B̂_i)² / Σ(B_i − B̄)²)
3. 両者の関係
-
**単回帰(1変数)**の場合、
理論的に R² = r² (相関係数の2乗)
→ つまり、「rの大きさを2乗して説明力として解釈」できる。 -
多変量回帰では、説明変数が複数になるため r では表せず、
R² のみが「モデル全体の説明力」を表す。