ビームサーチとchokudaiサーチをRustで実装してみた

はじめに

とりあえず記録．
アルゴリズムの具体的な説明は時間のあるときに追記します．

CodinGameの"The Travelling Salesman Problem"でTSPを解くプログラムを実装します．

下準備

コードは以下のようになっているはずです．

use std::io;

macro_rules! parse_input {
    ($x:expr, $t:ident) => ($x.trim().parse::<$t>().unwrap())
}

/**
 * Auto-generated code below aims at helping you parse
 * the standard input according to the problem statement.
 **/
fn main() {
    let mut input_line = String::new();
    io::stdin().read_line(&mut input_line).unwrap();
    let n = parse_input!(input_line, i32);
    for i in 0..n as usize {
        let mut input_line = String::new();
        io::stdin().read_line(&mut input_line).unwrap();
        let inputs = input_line.split(" ").collect::<Vec<_>>();
        let x = parse_input!(inputs[0], i32);
        let y = parse_input!(inputs[1], i32);
    }

    // Write an answer using println!("message...");
    // To debug: eprintln!("Debug message...");

    println!("0 2 1 3");
}

まずは，頂点を扱いやすくするため，構造体を定義しましょう．

#[derive(Debug, Clone, Copy)]
struct Point {
    id: usize,
    x: i32,
    y: i32,
}

impl Point {
    fn new(id: usize, x: i32, y: i32) -> Point {
        Point { id, x, y }
    }

    fn distance(&self, other: &Point) -> f64 {
        (((self.x - other.x).pow(2) + (self.y - other.y).pow(2)) as f64).sqrt()
    }
}

さて，初期のコードを見てみましょう．データの読み込みは一応されていますが，どこにも保存されていません．
main関数を弄ってもいいですが，読みやすさのことも考え，読み込み用の新しい関数を定義してしまいましょう．

impl Point {
    fn new(id: usize, x: i32, y: i32) -> Point {
        Point { id, x, y }
    }

    fn distance(&self, other: &Point) -> f64 {
        (((self.x - other.x).pow(2) + (self.y - other.y).pow(2)) as f64).sqrt()
    }

    fn import() -> Vec<Point> {
        let mut input_line = String::new();
        io::stdin().read_line(&mut input_line).unwrap();
        let n = parse_input!(input_line, i32);
        let mut points = Vec::new();
        for i in 0..n as usize {
            let mut input_line = String::new();
            io::stdin().read_line(&mut input_line).unwrap();
            let inputs = input_line.split(" ").collect::<Vec<_>>();
            let x = parse_input!(inputs[0], i32);
            let y = parse_input!(inputs[1], i32);
            points.push(Point::new(i, x, y));
        }
        points
    }
}

ビームサーチ

実装

use std::collections::{BinaryHeap, VecDeque};

fn beam_search(points: &Vec<Point>, beam_width: usize) -> Vec<usize> {
    let mut timer = Timer::new();

    let mut deq = VecDeque::new();
    deq.push_back((points[0], vec![0]));

    let mut ans_heap = BinaryHeap::new();

    loop {
        if deq.is_empty() {
            break;
        }
        let mut heap = BinaryHeap::new();

        loop {
            if deq.is_empty() {
                break;
            }
            let (point, path) = deq.pop_front().unwrap();
            for i in 0..points.len() {
                if path.contains(&i) {
                    continue;
                }
                heap.push((-points[i].distance(&point) as i32, i, path.clone()));
            }
        }
        for _ in 0..beam_width {
            if timer.get_time() >= TIMELIMIT {
                break;
            }
            if heap.is_empty() {
                break;
            }
            let (_dist, i, path) = heap.pop().unwrap();
            let mut new_path = path.clone();
            new_path.push(i);
            if new_path.len() == points.len() {
                new_path.push(0);
                ans_heap.push((-Point::length(points, &new_path), new_path));
            } else {
                deq.push_back((points[i], new_path));
            }
        }
    }

    let ans = ans_heap.pop().unwrap();

    return ans.1;
}

優先度付きキューにBinaryHeapを用いています．
BinaryHeapでは大きい順にソートされるため，距離はマイナスで保存すると短い順に取り出すことができます．

提出結果

ビーム幅は5にしました．

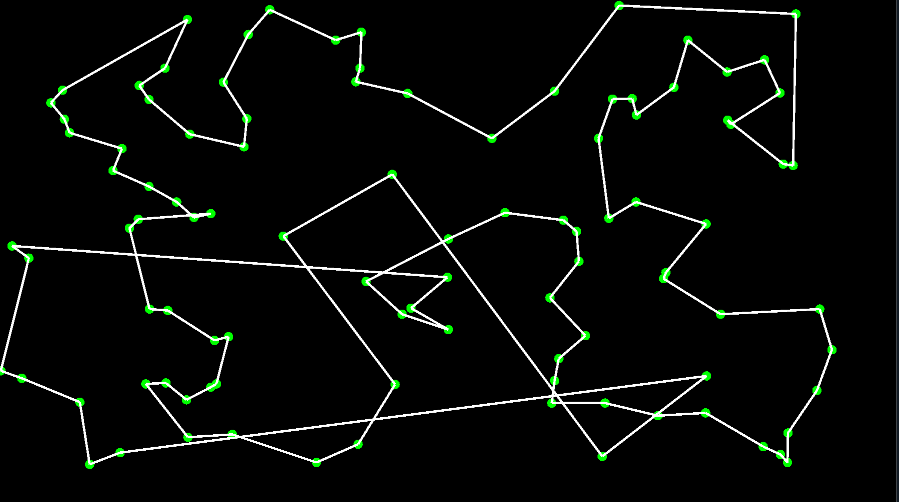
スコア（長さの合計）：260,395
上記の画像は頂点数＝100のもの．
ビーム幅を大きくしてみたらかえって悪化したケースも見られました．

chokudaiサーチ

実装

fn chokudai_search(points: &Vec<Point>, chokudai_width: usize, timer: &mut Timer) -> Vec<usize> {
    let mut heaps = vec![BinaryHeap::new(); points.len() + 1];
    heaps[1].push((0, vec![0]));
    loop {
        if timer.get_time() >= TIMELIMIT {
            break;
        }
        for t in 1..points.len() {
            if timer.get_time() >= TIMELIMIT {
                break;
            }
            for _ in 0..chokudai_width {
                if heaps[t].is_empty() {
                    break;
                }
                let (dist, path) = heaps[t].pop().unwrap();
                let point = points[path[path.len() - 1]];
                for i in 0..points.len() {
                    if path.contains(&i) {
                        continue;
                    }
                    let mut new_path = path.clone();
                    new_path.push(i);
                    heaps[t + 1].push((-Point::length(points, &new_path), new_path));
                    if timer.get_time() >= TIMELIMIT {
                        break;
                    }
                }
            }
        }
    }

    let mut ans = heaps[points.len()].pop().unwrap().1;
    ans.push(0);

    return ans;
}

時間いっぱい処理を回すため，TimerとTIMELIMITも定義しておきます．

const TIMELIMIT: f64 = 2.8;

fn get_time() -> f64 {
    let t = std::time::SystemTime::now()
        .duration_since(std::time::UNIX_EPOCH)
        .unwrap();
    t.as_secs() as f64 + t.subsec_nanos() as f64 * 1e-9
}

struct Timer {
    start_time: f64,
}

impl Timer {
    fn new() -> Timer {
        Timer {
            start_time: get_time(),
        }
    }

    fn get_time(&self) -> f64 {
        get_time() - self.start_time
    }

    #[allow(dead_code)]
    fn reset(&mut self) {
        self.start_time = 0.0;
    }
}

制限時間は5秒となっていますが，ギリギリにするとタイムアウトになるため，余裕を持たせてTIMELIMITは3秒にしました．

提出結果

スコア（長さの合計）：257,411
上記の画像は頂点数＝100のもの．

まとめ

単純な実装でもそれっぽい結果は得られました．
時間のあるときに効率のいい枝刈りの実装もできるといいなという気持ちになりました．