はじめに
シンセサイザーって良いですよね。
ちょっとツマミをいじればいろんな音が作れて、音を鳴らしてるだけでも楽しい。
ハードウェア、ソフトウェアともに音楽制作では様々なものが使用されており、音の出し方にも色んな方式がある。
実際の楽器のような音を鳴らすには、実際の楽器をサンプルした音源が多く利用されるが、
波形を1から生成する方式では生楽器ではありえないような音も出すことができる。
そっちの方が音を作ってるって感じがするよね。
波形を作るのは、基本的な仕組みとしては難しいものではなく、検索すればさまざまな解説を見つけることができる。
QiitaにもC言語でのシンセサイザーの解説やPythonのライブラリの記事などのある。
C言語でシンセサイザー作成入門(その1) - Qiita
Python で音楽を作って楽しもう - Qiita
シンセサイザーのようなリアルタイム性が重要なものはpythonなどのスクリプト言語よりもC言語などで書くべきなのだろうが、Cで波形作って音を鳴らせる環境を作るのは結構ややこしい。(とくにリアルタイムに自由に音階や音色を変えるの)
今回はできるだけ簡単に音作りを試せるように、鍵盤のGUI 付きのPythonコードでシンセサイザーの仕組みを紹介してみる。
基本的にコードをコピペすれば動くはず。
環境と鍵盤付きGUI作成
Python
Pyaudio
Opencv-python
Pyaudioは音を再生するのに使う。単に波形を作った後に再生するだけなら標準のwaveライブラリで出来るが、リアルタイムに再生するためにはこのライブラリが必要になる。この記事などを参考にpipでインストールする。
macOSにpyaudioをインストールする - Qiita
仕組みとしてはある程度のサンプルのかたまり(32、64、128とか。一般的にバッファーサイズという)ごとに波形を作り再生する。その際音の再生中にもプログラムを操作できるようにthreadingを使用してマルチスレッドで動作させる。
一方、opencvはguiに使う。(簡単にguiを作れる)
鍵盤の絵を書いておき、Opencvのマウス座標検知の仕組みを用いてどの鍵盤をクリックしたかを調べることで、その鍵盤に応じた音程の波形を生成する。
音程は波形の繰り返し周波数で決まり、ある音程nに対する周波数は以下の式で求められる。
$f = 440 \times 2^{(n-9)/12}$
ここでは真ん中の高さのドの音を基準(n=0)にしている。よって,レならn=2、オクターブ上のドはn=12みたいな感じ。(440という数字はNHKの時報にも使われるラの周波数でドはそこから-9となる。)
最も簡単な音の波形であるサイン波を鳴らすコードは以下のようになる。
2オクターブ分のキーボードが表示されるので、ある鍵盤をクリックするとその音が再生される。
関数synthesizeで波形を作るようにしている。
PCのキーボードのqを押すと終了する。
また鍵盤をクリックした後,押したまま画面外でクリックを離すと音を鳴らし続けることができるので,音を確認しながらパラメータを変えることが出来て便利。
音のオンとオフの切替時にプチプチっとした音が聞こえるが,これは切替時に波形が不連続になってしまい高周波のノイズが生成されてしまうためである。これを回避するためには,不連続にならないように徐々に音量を上げるようにするか,ローパスフィルターに通す必要がある(次項参照)。
import numpy as np
import pyaudio
import struct
import cv2
import threading
RATE=44100
bufsize = 32
# 鍵盤のGUI作成
ksx = 800
ksy = 200
keyboard = np.zeros([ksy,ksx,3])
keyboard[:,:,:] = 255
for i in range(15):
cv2.rectangle(keyboard, (int(ksx/15*i), 0), (int(ksx/15*(i+1)),ksy), (0, 0, 0), 5)
for i in range(15):
if i in {0,1,3,4,5,7,8,10,11,12}:
cv2.rectangle(keyboard, (int(ksx/15*i + ksx/27 ), 0), (int(ksx/15*(i+1) + ksx/33),int(ksy/2)), (0, 0, 0), -1)
cv2.namedWindow("keyboard", cv2.WINDOW_NORMAL)
# マウス位置による鍵盤選択
keyon = 0
pitch = 440
highkeys = np.array([0,1,1,3,3,4,5,6,6,8,8,10,10,11, 12,13,13,15,15,16,17,18,18,20,20,22,22,23, 24,24])
lowkeys = np.array([0,2,4,5,7,9,11, 12,14,16,17,19,21,23, 24])
def mouse_event(event, x, y, flags, param):
global keyon,pitch
if event == cv2.EVENT_LBUTTONDOWN:
keyon = 1
if y >= ksy/2:
note = lowkeys[int(15.0*x/ksx)]
elif y < ksy/2:
note = highkeys[int(30.0*x/ksx)]
pitch = 440*(np.power(2,(note-9)/12))
elif event == cv2.EVENT_LBUTTONUP :
keyon = 0
cv2.setMouseCallback("keyboard", mouse_event)
# 波形生成
x=np.arange(bufsize)
pos = 0
def synthesize():
global pos
#位相計算
t = pitch * (x+pos) / RATE
t = t - np.trunc(t)
pos += bufsize
wave = np.sin(2.0*np.pi*t)
if keyon == 1:
velosity = 1.0
else:
velosity = 0.0
wave = velosity * wave
return wave
# 波形再生
playing = 1
def audioplay():
print ("Start Streaming")
p=pyaudio.PyAudio()
stream=p.open(format = pyaudio.paInt16,
channels = 1,
rate = RATE,
frames_per_buffer = bufsize,
output = True)
while stream.is_active():
buf = synthesize()
buf = (buf * 32768.0).astype(np.int16)#16ビット整数に変換
buf = struct.pack("h" * len(buf), *buf)
stream.write(buf)
if playing == 0:
break
stream.stop_stream()
stream.close()
p.terminate()
print ("Stop Streaming")
# 画面描画
if __name__ == "__main__":
thread = threading.Thread(target=audioplay)
thread.start()
while (True):
cv2.imshow("keyboard", keyboard)
k = cv2.waitKey(100) & 0xFF
if k == ord('q'):
playing = 0
break
cv2.destroyAllWindows()
減算方式
まずは減算方式の波形生成について。
減算方式というのは,倍音を豊富に含んだベースとなる波形から倍音をカットすることでさまざまな音を出すという方式。アナログシンセは基本的にこの方式である。
基本的にはオシレーター,フィルター,エンベロープの3つの要素に分けることができる。
オシレーター
オシレータは発振器のことで,さまざまな種類の繰り返し波形を出力する。
先ほどのサイン波はフーリエ変換してみると単一の周波数しか持っていない。
音色というのは基本的にその音程の周波数成分に対してどのような倍音を持っているかで決まるため、倍音をどう作るかが重要になる。
サイン波ではない違う繰り返しの波形を用いるとどうなるか。
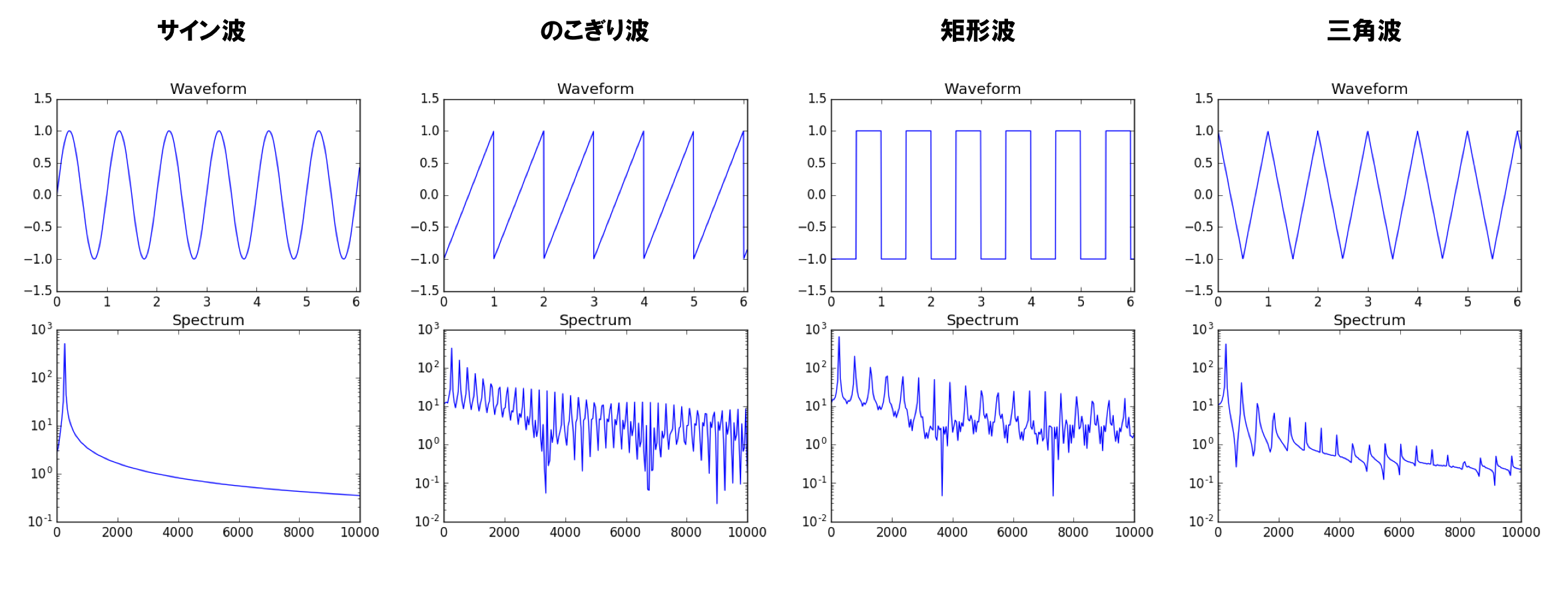
下図にサイン波、のこぎり波、矩形波、三角波の波形とフーリエ変換したスペクトルを示す。
サイン波のスペクトルには1つの周波数成分しかないが,のこぎり波はすべての倍数の周波数成分が、矩形波は奇数倍の周波数成分が、三角波は矩形波よりも小さい奇数倍の周波数成分が含まれていことがわかる。
下記のコードで鳴らしてみるとわかるが,
サイン波はポーって感じの単純な音,のこぎり波はブラスなどのような金属的な音、矩形波はクラリネットや笛のような音、三角波は丸っこい音がする。
フィルター
フィルターによってサイン波以外で生成される倍音をカットしていく。高周波成分をカットするローパスフィルター,低周波数をカットするハイパスフィルター,特定の帯域をカットするバンドパスフィルターなどが用いられるが、最も基本となるものはローパスフィルターである。
デジタルフィルタでよく使われる2次のIIRフィルタが下記のテキストにまとめられている。
http://www.musicdsp.org/files/Audio-EQ-Cookbook.txt
ローパスフィルタの周波数に対する透過率は下図のようになる。
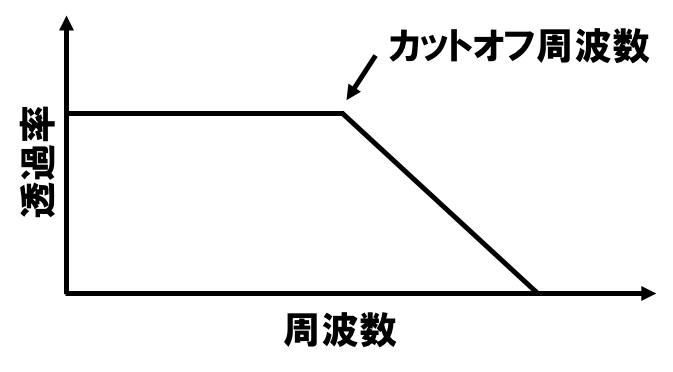
ここで,減衰を始める周波数をカットオフ周波数という。
高周波成分をカットするので,カットオフ周波数が小さくなるほど角の取れたまろやかな音に変化していく。
エンベロープ
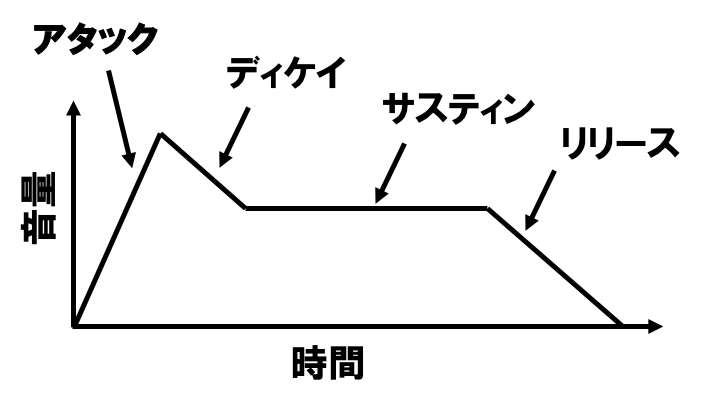
図のように
アタック:鍵盤を押した時の音の立ち上がりのスピード、
ディケイ:立ち上がりのピークからの減衰
サスティン:鍵盤を押している間に音が持続する際の音量
リリース:鍵盤を放してからの減衰のスピード
ADSR と言われるパラメータで決めることができる。
たとえば,アタックを小さめにして押してからゆっくりと音量が上がるようにするとバイオリンのようになり,リリースを小さめにして鍵盤を離してからも音が長く持続するようにするとベルを鳴らしたようにすることができる。
ここではアタックのスピードとリリースのスピードを変更できるように実装した。
減算方式のシンセサイザーを試すコードは以下の通り。
スライダーを操作することで各パラメータを変えることができる。
opencvのguiのスライダーは数値が出ないためわかりにくいが左端が0となっている。
スライダー1(Waveform type)は,
0:サイン波
1:のこぎり波
2:矩形波
3:三角波
スライダー2(Attack)がアタックのスピード(0〜255)
スライダー3(Release)がリリースのスピード(0〜255)
スライダー4(Lowpass freq)がローパスフィルターのカット周波数(0〜255)
これだけでも多彩な音を作ることができるのがわかる。
実際のシンセサイザーではフィルターの特製も時間的に変化させたりすることでさらに面白い音を作ることができるようになっている。
import numpy as np
import pyaudio
import struct
import cv2
import threading
RATE=44100
bufsize = 32
# 鍵盤のGUI作成
ksx = 800
ksy = 200
keyboard = np.zeros([ksy,ksx,3])
keyboard[:,:,:] = 255
for i in range(15):
cv2.rectangle(keyboard, (int(ksx/15*i), 0), (int(ksx/15*(i+1)),ksy), (0, 0, 0), 5)
for i in range(15):
if i in {0,1,3,4,5,7,8,10,11,12}:
cv2.rectangle(keyboard, (int(ksx/15*i + ksx/27 ), 0), (int(ksx/15*(i+1) + ksx/33),int(ksy/2)), (0, 0, 0), -1)
cv2.namedWindow("keyboard", cv2.WINDOW_NORMAL)
# 各種パラメータ用スライダーの設定
sl=np.array([0,150,150,255])
slName = np.array(['Wave_type',
'Attack',
'Release',
'Lowpass_freq'])
def changeBar(val):
global sl
for i in range(4):
sl[i] = cv2.getTrackbarPos(slName[i], "keyboard")
cv2.createTrackbar(slName[0], "keyboard", 0, 3, changeBar)
cv2.createTrackbar(slName[1], "keyboard", 0, 255, changeBar)
cv2.createTrackbar(slName[2], "keyboard", 0, 255, changeBar)
cv2.createTrackbar(slName[3], "keyboard", 0, 255, changeBar)
for i in range(4):
cv2.setTrackbarPos(slName[i], "keyboard", sl[i])
# マウス位置による鍵盤選択
keyon = 0
pre_keyon = 0
pitch = 440
velosity = 0.0
highkeys = np.array([0,1,1,3,3,4,5,6,6,8,8,10,10,11, 12,13,13,15,15,16,17,18,18,20,20,22,22,23, 24,24])
lowkeys = np.array([0,2,4,5,7,9,11, 12,14,16,17,19,21,23, 24])
def mouse_event(event, x, y, flags, param):
global keyon,pre_keyon,pitch,velosity
if event == cv2.EVENT_LBUTTONDOWN:
keyon = 1
if y >= ksy/2:
note = lowkeys[int(15.0*x/ksx)]
elif y < ksy/2:
note = highkeys[int(30.0*x/ksx)]
pitch = 440*(np.power(2,(note-9)/12))
elif event == cv2.EVENT_LBUTTONUP :
keyon = 0
if pre_keyon ==0 and keyon ==1:
velosity = 0.0
pre_keyon = keyon
cv2.setMouseCallback("keyboard", mouse_event)
# ローパスフィルター
lpfbuf=np.zeros(4)
outwave=np.zeros(bufsize)
def lowpass(wave):
global lpfbuf,outwave
w0 = 2.0*np.pi*(200+(sl[3]/255.0)**2*20000)/RATE;
Q = 1.0
alpha = np.sin(w0)/(2.0*Q)
a0 = (1 + alpha)
a1 = -2*np.cos(w0)/a0
a2 = (1 - alpha)/a0
b0 = (1 - np.cos(w0))/2/a0
b1 = (1 - np.cos(w0))/a0
b2 = (1 - np.cos(w0))/2/a0
for i in range(bufsize):
outwave[i] = b0*wave[i]+b1*lpfbuf[1]+b2*lpfbuf[0]-a1*lpfbuf[3]-a2*lpfbuf[2]
lpfbuf[0] = lpfbuf[1]
lpfbuf[1] = wave[i]
lpfbuf[2] = lpfbuf[3]
lpfbuf[3] = outwave[i]
return outwave
# 波形生成
x=np.arange(bufsize)
pos = 0
def synthesize():
global pos,velosity
#位相計算
t = pitch * (x+pos) / RATE
t = t - np.trunc(t)
pos += bufsize
#基本波形選択
if sl[0]==1:#のこぎり波
wave = t*2.0-1.0
elif sl[0]==2:#矩形波
wave = np.zeros(bufsize);wave[t<=0.5]=-1;wave[t>0.5]=1;
elif sl[0]==3:#三角波
wave = np.abs(t*2.0-1.0)*2.0-1.0
else:#サイン波
wave = np.sin(2.0*np.pi*t)
#エンベロープ設定
if keyon == 1:
vels = velosity + x * ((sl[1]/1000)**3+0.00001)
vels[vels>0.6] = 0.6
else:
vels = velosity - x * ((sl[2]/1000)**3+0.00001)
vels[vels<0.0] = 0.0
velosity = vels[-1]
wave = vels * wave
#ローパスフィルター
wave = lowpass(wave)
return wave
# 波形再生
playing = 1
def audioplay():
print ("Start Streaming")
p=pyaudio.PyAudio()
stream=p.open(format = pyaudio.paInt16,
channels = 1,
rate = RATE,
frames_per_buffer = bufsize,
output = True)
while stream.is_active():
buf = synthesize()
buf = (buf * 32768.0).astype(np.int16)#16ビット整数に変換
buf = struct.pack("h" * len(buf), *buf)
stream.write(buf)
if playing == 0:
break
stream.stop_stream()
stream.close()
p.terminate()
print ("Stop Streaming")
# 画面描画
if __name__ == "__main__":
thread = threading.Thread(target=audioplay)
thread.start()
while (True):
cv2.imshow("keyboard", keyboard)
k = cv2.waitKey(100) & 0xFF
if k == ord('q'):
playing = 0
break
cv2.destroyAllWindows()
FM方式
FMとは周波数変調のこと。
アナログシンセでは作れなかった複雑な音色が実現できるようになり,80〜90年台にかけて一世を風靡したらしい。ヤマハのDX7はモデリングを含め現在でも使用される名機である。
先ほど使用したサイン波の式は$f$を音程の周波数とすると
$sin(2 \pi f t)$
である。ここサインの位相をさらにサイン派で変調すると以下のような式になる。
$sin(2 \pi t + a \times sin(2 \pi f b t))$
$a$は変調の強さ,$b$は変調周波数の音程周波数に対する比率。
変調する側をモジュレータ,変調される側の音をだすためのオシレーターをキャリアとも呼ぶ。
こうするとどうなるかは実際の波形とスペクトルを見るとわかりやすい。
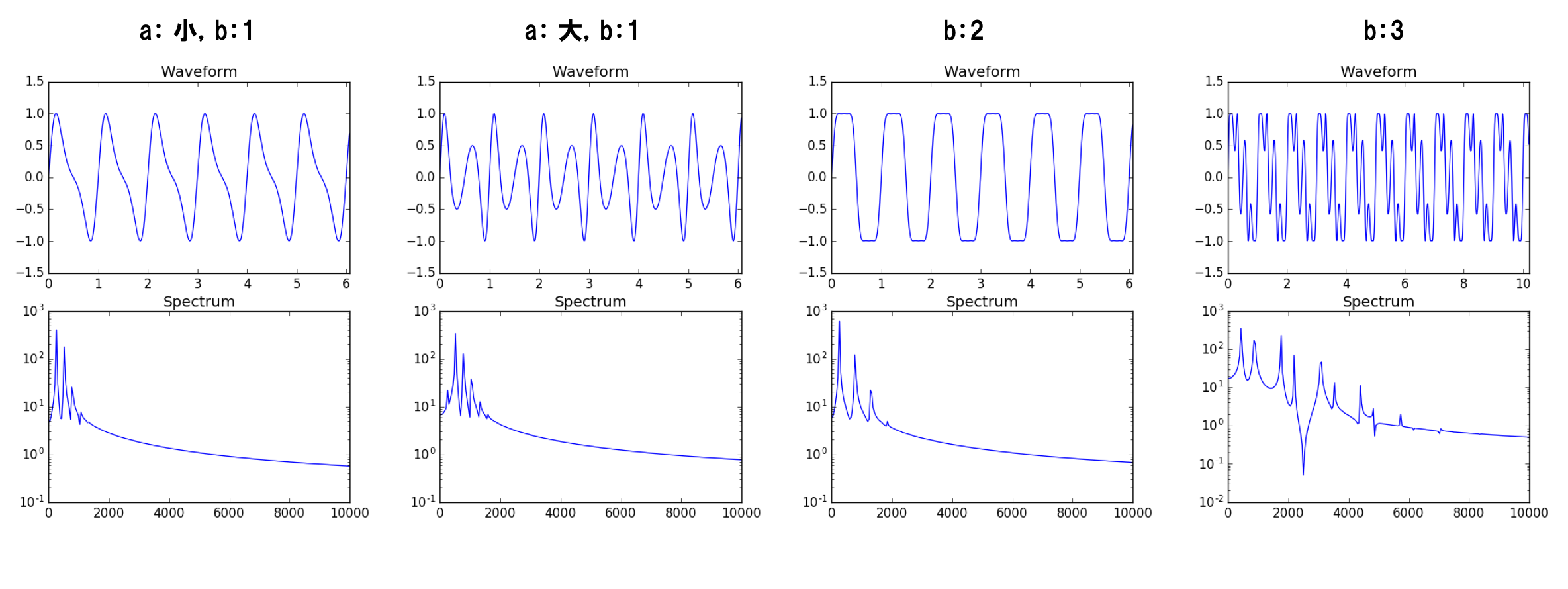
変調する周波数や振幅を変えると全く異なる波形、スペクトルになることがわかる。
FM方式でも基準周波数の倍音が作られているが、変調のしかたを変えると驚くほど波形が変わるため減算方式では作れないような波形も作り出すことができる。基本的には音程周波数の倍数になるような周波数かわずかにずらした周波数を用いる。また,図の左から1番目と3番めはそれぞれノコギリ波,矩形波に似ていることがわかる。ただのサイン波でもFM方式を用いてうまくパラメータを設定するとノコギリ波,矩形波を作ることもできる。
変調のためのサイン派も1つだけでなく、変調するためのサイン波をさらにちがうサイン波で変調したり、二系統の波形を作って合算する、フィードバック構造にする、などいろいろな組み合わせ(アルゴリズム)が用いられている。DX7では6個のオシレータで32種類のアルゴリズムが搭載されており,多彩な音色を作り出すことができる。
FM方式の音作りは非常に難しくかなりのノウハウが必要になる。
ここではもっとも単純な1つのキャリアと1つのモジュレータを用いた実装をした。
これだけでも多彩な音作りが可能で,たとえばモジュレータの周波数比率を11にして,アタックを大きくリリースを小さくすると鐘のような音を作ることができる。
import numpy as np
import pyaudio
import struct
import cv2
import threading
RATE=44100
bufsize = 32
# 鍵盤のGUI作成
ksx = 800
ksy = 200
keyboard = np.zeros([ksy,ksx,3])
keyboard[:,:,:] = 255
for i in range(15):
cv2.rectangle(keyboard, (int(ksx/15*i), 0), (int(ksx/15*(i+1)),ksy), (0, 0, 0), 5)
for i in range(15):
if i in {0,1,3,4,5,7,8,10,11,12}:
cv2.rectangle(keyboard, (int(ksx/15*i + ksx/27 ), 0), (int(ksx/15*(i+1) + ksx/33),int(ksy/2)), (0, 0, 0), -1)
cv2.imshow("keyboard", keyboard)
# 各種パラメータ用スライダーの設定
sl=np.array([150,150,0,1])
slName = np.array(['Attack',
'Release',
'FM_amp',
'FM_freq'])
def changeBar(val):
global sl
for i in range(4):
sl[i] = cv2.getTrackbarPos(slName[i], "keyboard")
cv2.namedWindow("keyboard", cv2.WINDOW_NORMAL)
cv2.createTrackbar(slName[0], "keyboard", 0, 255, changeBar)
cv2.createTrackbar(slName[1], "keyboard", 0, 255, changeBar)
cv2.createTrackbar(slName[2], "keyboard", 0, 255, changeBar)
cv2.createTrackbar(slName[3], "keyboard", 0, 11, changeBar)
for i in range(4):
cv2.setTrackbarPos(slName[i], "keyboard", sl[i])
# マウス位置による鍵盤選択
keyon = 0
pre_keyon = 0
pitch = 440
velosity = 0.0
highkeys = np.array([0,1,1,3,3,4,5,6,6,8,8,10,10,11, 12,13,13,15,15,16,17,18,18,20,20,22,22,23, 24,24])
lowkeys = np.array([0,2,4,5,7,9,11, 12,14,16,17,19,21,23, 24])
def mouse_event(event, x, y, flags, param):
global keyon,pre_keyon,pitch,velosity
if event == cv2.EVENT_LBUTTONDOWN:
keyon = 1
if y >= ksy/2:
note = lowkeys[int(15.0*x/ksx)]
elif y < ksy/2:
note = highkeys[int(30.0*x/ksx)]
pitch = 440*(np.power(2,(note-9)/12))
elif event == cv2.EVENT_LBUTTONUP :
keyon = 0
if pre_keyon ==0 and keyon ==1:
velosity = 0.0
pre_keyon = keyon
cv2.setMouseCallback("keyboard", mouse_event)
# 波形生成
x=np.arange(bufsize)
pos = 0
def synthesize():
global pos,velosity
#位相計算
t = pitch * (x+pos) / RATE
t = t - np.trunc(t)
pos += bufsize
wave = np.sin(2.0*np.pi*t + sl[2]/100.0 * np.sin(2.0*np.pi*t*sl[3]))
#エンベロープ設定
if keyon == 1:
vels = velosity + x * ((sl[0]/1000)**3+0.00001)
vels[vels>0.6] = 0.6
else:
vels = velosity - x * ((sl[1]/1000)**3+0.00001)
vels[vels<0.0] = 0.0
velosity = vels[-1]
wave = vels * wave
return wave
# 波形再生
playing = 1
def audioplay():
print ("Start Streaming")
p=pyaudio.PyAudio()
stream=p.open(format = pyaudio.paInt16,
channels = 1,
rate = RATE,
frames_per_buffer = bufsize,
output = True)
while stream.is_active():
buf = synthesize()
buf = (buf * 32768.0).astype(np.int16)#16ビット整数に変換
buf = struct.pack("h" * len(buf), *buf)
stream.write(buf)
if playing == 0:
break
stream.stop_stream()
stream.close()
p.terminate()
print ("Stop Streaming")
# 画面描画
if __name__ == "__main__":
thread = threading.Thread(target=audioplay)
thread.start()
while (True):
cv2.imshow("keyboard", keyboard)
k = cv2.waitKey(100) & 0xFF
if k == ord('q'):
playing = 0
break
cv2.destroyAllWindows()
ディレイエフェクト
シンセサイザーでは音色を作った後エフェクターに接続することで音色をさらに煌びやかにしている。
今回はディレイについて説明する。
ディレイはエコーとも呼ばれ、やまびこのような繰り返し効果を付けることができる。
つまりある音を鳴らした後、音をコピーしておき遅延を与えて後の波形に足し合わせる。足し合わせるときの音量と遅延量でディレイ効果を変化させることが出来る。遅延量をディレイタイム,音をコピーする時の減衰係数をフィードバックという。フィードバックが大きいほど同じ音が何回も繰り返し再生される。
これを実装するには、配列の先頭と後ろが繋がったループ構造をもつリングバッファを使用する。リングバッファのインデックスつまり現在位置は音のサンプルを再生するたびにずらしていく。ある音のサンプルを再生する時、設定した遅延分うしろの位置のリングバッファにそのサンプルを減衰係数をかけて挿入する。再生時には作った波形とリングバッファの値を足し合わせて出力する。pythonではnumpy.rollを使えば簡潔に書ける。
コード
ディレイを実装したコードは以下の通り。
設定出来るパラメーターは
スライダー1(Waveform type),0:サイン波,1:のこぎり波,2:矩形波,3:三角波,4:FM方式
スライダー2(Attack)がアタックのスピード(0〜255)
スライダー3(Release)がリリースのスピード(0〜255)
スライダー4(Lowpass freq)がローパスフィルターのカット周波数(0〜255)
スライダー5(FM amp)がFM方式を選んだ場合の変調の強さ(0〜255)
スライダー6(FM freq)がFM方式を選んだ場合の変調周波数の倍率(0〜11)
スライダー7(Delay time)がディレイの遅延量(0〜255)
スライダー8(Delay feedback)がディレイの大きさ(0〜255)
更にPCのキーボードのsを押すと,その時のパラメータによって出力される音の波形とスペクトルをmatplotlibを使って別ウィンドウに表示することができる。
上記で説明したWaveform typeやローパスフィルターによって波形やスペクトルがどのように変化するか確認すると,より視覚的にわかりやすい。
import numpy as np
import pyaudio
import struct
import cv2
import threading
import matplotlib.pyplot as plt
RATE=44100
bufsize = 32
# 鍵盤のGUI作成
ksx = 800
ksy = 200
keyboard = np.zeros([ksy,ksx,3])
keyboard[:,:,:] = 255
for i in range(15):
cv2.rectangle(keyboard, (int(ksx/15*i), 0), (int(ksx/15*(i+1)),ksy), (0, 0, 0), 5)
for i in range(15):
if i in {0,1,3,4,5,7,8,10,11,12}:
cv2.rectangle(keyboard, (int(ksx/15*i + ksx/27 ), 0), (int(ksx/15*(i+1) + ksx/33),int(ksy/2)), (0, 0, 0), -1)
cv2.imshow("keyboard", keyboard)
# 各種パラメータ用スライダーの設定
sl=np.array([0,150,150,255,0,0,0,0])
slName = np.array(['Wave_type',
'Attack',
'Release',
'Lowpass_freq',
'FM_amp',
'FM_freq',
'Delay_time',
'Delay_feedback'])
def changeBar(val):
global sl
for i in range(8):
sl[i] = cv2.getTrackbarPos(slName[i], "keyboard")
cv2.namedWindow("keyboard", cv2.WINDOW_NORMAL)
cv2.createTrackbar(slName[0], "keyboard", 0, 4, changeBar)
cv2.createTrackbar(slName[1], "keyboard", 0, 255, changeBar)
cv2.createTrackbar(slName[2], "keyboard", 0, 255, changeBar)
cv2.createTrackbar(slName[3], "keyboard", 0, 255, changeBar)
cv2.createTrackbar(slName[4], "keyboard", 0, 255, changeBar)
cv2.createTrackbar(slName[5], "keyboard", 0, 11, changeBar)
cv2.createTrackbar(slName[6], "keyboard", 0, 255, changeBar)
cv2.createTrackbar(slName[7], "keyboard", 0, 255, changeBar)
for i in range(8):
cv2.setTrackbarPos(slName[i], "keyboard", sl[i])
# マウス位置による鍵盤選択
keyon = 0
pre_keyon = 0
pitch = 440
velosity = 0.0
highkeys = np.array([0,1,1,3,3,4,5,6,6,8,8,10,10,11, 12,13,13,15,15,16,17,18,18,20,20,22,22,23, 24,24])
lowkeys = np.array([0,2,4,5,7,9,11, 12,14,16,17,19,21,23, 24])
def mouse_event(event, x, y, flags, param):
global keyon,pre_keyon,pitch,velosity
if event == cv2.EVENT_LBUTTONDOWN:
keyon = 1
if y >= ksy/2:
note = lowkeys[int(15.0*x/ksx)]
elif y < ksy/2:
note = highkeys[int(30.0*x/ksx)]
pitch = 440*(np.power(2,(note-9)/12))
elif event == cv2.EVENT_LBUTTONUP :
keyon = 0
if pre_keyon ==0 and keyon ==1:
velosity = 0.0
pre_keyon = keyon
cv2.setMouseCallback("keyboard", mouse_event)
# ローパスフィルター
lpfbuf=np.zeros(4)
outwave=np.zeros(bufsize)
def lowpass(wave):
global lpfbuf,outwave
w0 = 2.0*np.pi*(200+(sl[3]/255.0)**2*20000)/RATE;
Q = 1.0
alpha = np.sin(w0)/(2.0*Q)
a0 = (1 + alpha)
a1 = -2*np.cos(w0)/a0
a2 = (1 - alpha)/a0
b0 = (1 - np.cos(w0))/2/a0
b1 = (1 - np.cos(w0))/a0
b2 = (1 - np.cos(w0))/2/a0
for i in range(bufsize):
outwave[i] = b0*wave[i]+b1*lpfbuf[1]+b2*lpfbuf[0]-a1*lpfbuf[3]-a2*lpfbuf[2]
lpfbuf[0] = lpfbuf[1]
lpfbuf[1] = wave[i]
lpfbuf[2] = lpfbuf[3]
lpfbuf[3] = outwave[i]
return outwave
# ディレイ
ringbuf = np.zeros(50000)#最大ディレイタイムは50000/RATE秒
def delay(wave):
global ringbuf
delaytime = sl[6]/255.0 * 1.0
feedback = sl[7]/255.0 * 0.7
dryandwet = feedback/2.0
writepoint = int(delaytime*RATE)
ringbuf = np.roll(ringbuf,-bufsize)
ringbuf[writepoint:writepoint+bufsize] = wave + feedback * ringbuf[:bufsize]
outwave = (1-dryandwet) * wave + dryandwet * ringbuf[:bufsize]
return outwave
# 波形生成
x=np.arange(bufsize)
pos = 0
def synthesize():
global pos,velosity
#位相計算
t = pitch * (x+pos) / RATE
t = t - np.trunc(t)
pos += bufsize
#基本波形選択
if sl[0]==1:#のこぎり波
wave = t*2.0-1.0
elif sl[0]==2:#矩形波
wave = np.zeros(bufsize);wave[t<=0.5]=-1;wave[t>0.5]=1;
elif sl[0]==3:#三角波
wave = np.abs(t*2.0-1.0)*2.0-1.0
elif sl[0]==4:#FM変調
wave = np.sin(2.0*np.pi*t + sl[4]/100.0 * np.sin(2.0*np.pi*t*sl[5]))
else:#サイン波
wave = np.sin(2.0*np.pi*t)
#エンベロープ設定
if keyon == 1:
vels = velosity + x * ((sl[1]/1000)**3+0.00001)
vels[vels>0.6] = 0.6
else:
vels = velosity - x * ((sl[2]/1000)**3+0.00001)
vels[vels<0.0] = 0.0
velosity = vels[-1]
wave = vels * wave
#ローパスフィルター
wave = lowpass(wave)
return wave
# 波形再生
playing = 1
def audioplay():
print ("Start Streaming")
p=pyaudio.PyAudio()
stream=p.open(format = pyaudio.paInt16,
channels = 1,
rate = RATE,
frames_per_buffer = bufsize,
output = True)
while stream.is_active():
buf = synthesize()
buf = delay(buf)
buf = (buf * 32768.0).astype(np.int16)#16ビット整数に変換
buf = struct.pack("h" * len(buf), *buf)
stream.write(buf)
if playing == 0:
break
stream.stop_stream()
stream.close()
p.terminate()
print ("Stop Streaming")
# 波形とスペクトル画像生成
def waveformAndSpectrum():
sampleN = 1024
t0 = pitch * np.arange(sampleN) / RATE
t = t0 - np.trunc(t0)
#基本波形選択
if sl[0]==1:#のこぎり波
wave = t*2.0-1.0
elif sl[0]==2:#矩形波
wave = np.zeros(bufsize);wave[t<=0.5]=-1;wave[t>0.5]=1;
elif sl[0]==3:#三角波
wave = np.abs(t*2.0-1.0)*2.0-1.0
elif sl[0]==4:#FM変調
wave = np.sin(2.0*np.pi*t + sl[4]/100.0 * np.sin(2.0*np.pi*t*sl[5]))
else:#サイン波
wave = np.sin(2.0*np.pi*t)
if sl[3] < 250:#ローパスフィルター
outwave=np.zeros(sampleN)
w0 = 2.0*np.pi*(200+(sl[3]/255.0)**2*20000)/RATE;
Q = 1.0
alpha = np.sin(w0)/(2.0*Q)
a0 = (1 + alpha)
a1 = -2*np.cos(w0)/a0
a2 = (1 - alpha)/a0
b0 = (1 - np.cos(w0))/2/a0
b1 = (1 - np.cos(w0))/a0
b2 = (1 - np.cos(w0))/2/a0
lpfbuf2=np.zeros(4)
for i in range(sampleN):
outwave[i] = b0*wave[i]+b1*lpfbuf2[1]+b2*lpfbuf2[0]-a1*lpfbuf2[3]-a2*lpfbuf2[2]
lpfbuf2[0] = lpfbuf2[1]
lpfbuf2[1] = wave[i]
lpfbuf2[2] = lpfbuf2[3]
lpfbuf2[3] = outwave[i]
else:
outwave = wave
Spectrum = abs(np.fft.fft(outwave))
frq = np.fft.fftfreq(sampleN,1.0 / RATE)
plt.clf()
plt.subplot(2,1,1)
plt.title("Waveform")
plt.plot(t0,outwave)
plt.xlim([0,pitch * sampleN / RATE])
plt.ylim([-1.5, 1.5])
plt.subplot(2,1,2)
plt.title("Spectrum")
plt.yscale("log")
plt.plot(frq[:int(sampleN/2)],Spectrum[:int(sampleN/2)])
plt.xlim([0,10000])
plt.pause(1)
# 画面描画
if __name__ == "__main__":
thread = threading.Thread(target=audioplay)
thread.start()
while (True):
cv2.imshow("keyboard", keyboard)
k = cv2.waitKey(100) & 0xFF
if k == ord('q'):
playing = 0
break
if k == ord('s'):
waveformAndSpectrum()
cv2.destroyAllWindows()
まとめ
シンセサイザーの基本的な音の作り方を、出来るだけシンプルなgui付きのPythonのコードでまとめた。
今回は実装しなかったディケイ、サスティンやローパス以外のフィルター、フィルターの時間的な変化、FM方式の他のアルゴリズム、他のエフェクター、など、実際のシンセサイザーではたくさんのパラメーターによって無限の音作りが出来る。
さらに今回のは単音しか鳴らないモノフォニックシンセであるが、和音を鳴らすためには複数の音を同時になるようにする必要もある。
また、guiが簡単に作れるかと思いOpenCVを用いたが、パラメーター変更用のスライダーの位置がなぜか順番通りにならずバラバラになり、設定方法がわからなかった。Macだけ?
もし順番の指定方法がわかる方がいれば教えていただきたいです。