LoginSignup
150
153
BrainPadAdvent Calendar 2023Day 4
@_jintainBrainPad Inc.

効果検証のための因果推論手法のチートシート

Last updated at Posted at 2023-12-04

効果検証においてABテストによる単純比較以上のことをやろうすると、因果推論の各種手法を用いることになります。しかし、因果推論は主義や用語などが統一されておらず、いつ何を使えばいいかが分からないというハードルがあります。

そんな因果推論の手法を整理し、初～中級者にとって学習・活用の見通しが立てやすいようにまとめたものが本記事です。

2023/12/6追記
もともとこの記事は「もう迷わない！効果検証のための因果推論手法のチートシート」というタイトルだったのですが、"迷わない" はどう考えても言い過ぎだったので、タイトルを修正しました。沢山手法があるけど違いが分からなくて混乱しがち、というのが執筆のモチベーションです。むしろ 迷子のお伴 として活用していただけると幸いです。

特にフローチャートの部分は、これに従っておけばOKという主張ではなく、あくまで手法間の関係を整理するためのもの、そしてこういう整理の仕方をしている人間がいるという1例としてご認識ください。各手法が満たすべき仮定を書ききれていない部分も大いにありますし、何を使うべきかはこういう風に画一的に決まるものではないので、実際に因果推論を行う際は各手法についてより専門的な文献を見ることを推奨します。

本記事は３つのコンテンツからなります。

  1. 手法の比較表
  2. 各手法のざっくりビジュアル解説
  3. 手法のフローチャート的なもの

お断り

あくまで一意見です。すべての手法を使ったことがあるわけではないので正確でない記述を含む可能性が高いです。一応、働いている場所的に、比較的多くビジネスでのユースケースを見ているほうだとは思います。もちろん他の方の見識も参考にさせていただいており、最後にまとめてリンクを記載しています

なお、

  • Pearl流ではなくRubin流（Potential Outcomeフレームワーク）
  • ベイズではなく頻度論
  • Binaryの介入（ある介入をした／しないときの違いを知りたい）

を基本としています。理由は使われる機会が多いのと、あとは単に筆者の知識不足です。本記事で紹介するものと似たような手法がベイズだったりPearl流でも存在したり、構成できるはずです。連続の介入（例：価格をいくらにするか、広告の出稿量をどのくらいにするか）は多少扱いが違うので、勉強して整理が追い付いたら追記する可能性があります。

また本記事では、各手法の詳細については取り扱いません1。なお、今回取り扱わなかったけど耳にする手法についての簡単な紹介を、以下折りたたんでおきます。

展開
  • mediation analysis
    • 媒介（どのような経路で効果が起こるか）を分析する手法
    • 詳しくないが、仮定がかなり厳しいイメージがあり、使いどころをあまり聞いたことがない
  • bunching analysis
    • RDDのように閾値で介入有無が変わる際に、どの程度閾値を超えるための操作が行われるかを測る手法
    • ビジネスにおいては、活用して嬉しい対象が狭い印象
  • front door
    • Pearl流の因果推論でよく聞く手法
    • あまり活用例を聞いたことがないので割愛
  • bandit
    • 探索と活用のバランスをとりながら、動的に実験を最適化するためのもの
    • どちらかというと手法というよりは問題設定を指す言葉で、今回見たい問題設定とは異なる
  • uplift
    • これも問題設定の総称であり、推定手法をどう活用するかの話なので明示的には書いていない

▲ 展開ここまで

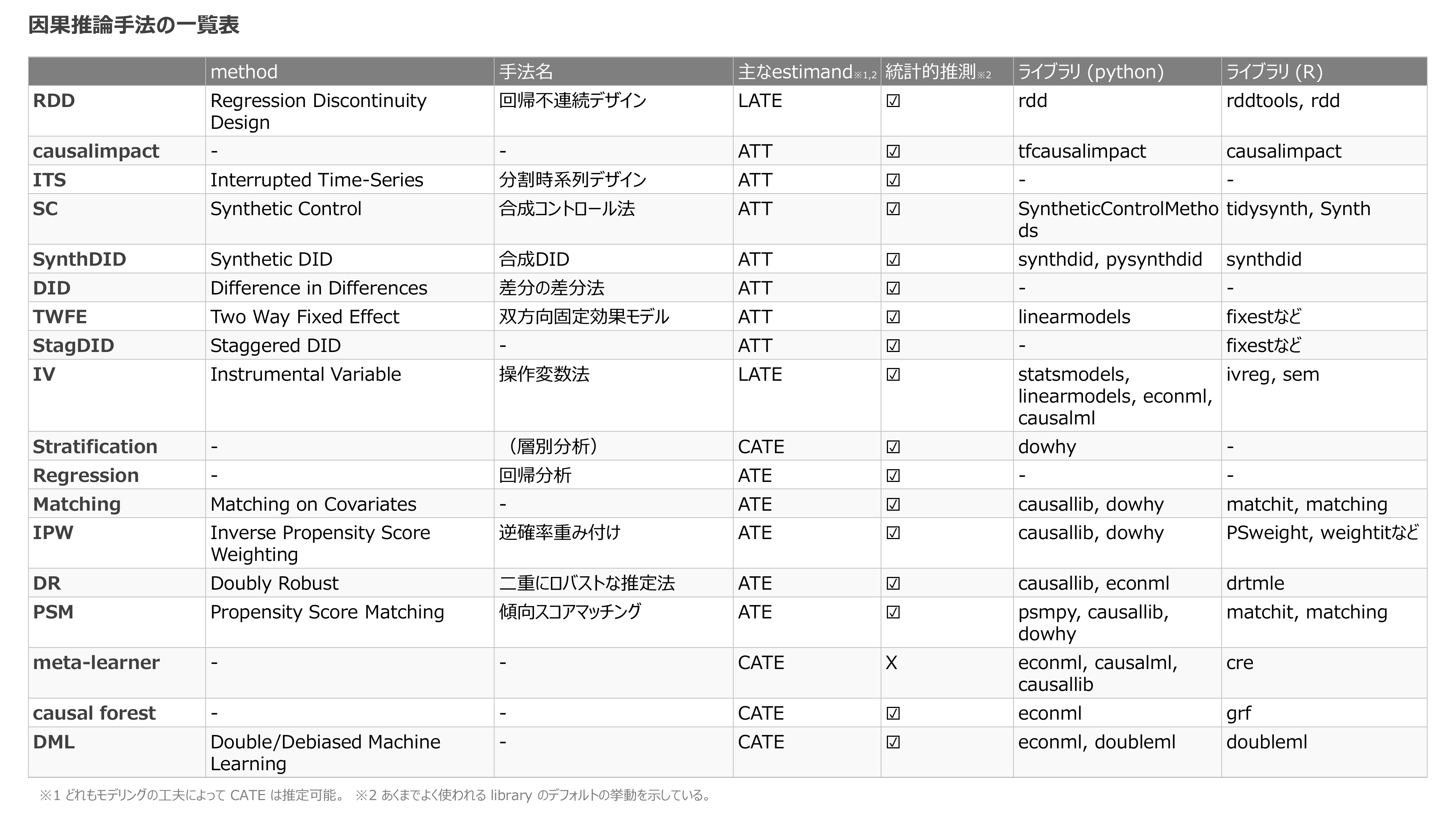
本記事で紹介する手法の一覧

page_2.png

  • 日本語、英語、略称どれも、人によって違う言葉を使うものがあります
    • たとえば、DID/DiD/DDなど
  • 本当はここに各手法に必要な仮定も入れたいのですが、そこまでは手が回らず。。すいません
  • ライブラリのドキュメントやGithubなどへのリンクは、以下の説明中に記載しています
  • 当然ですが、世の中に存在するすべての手法を網羅している訳ではないです

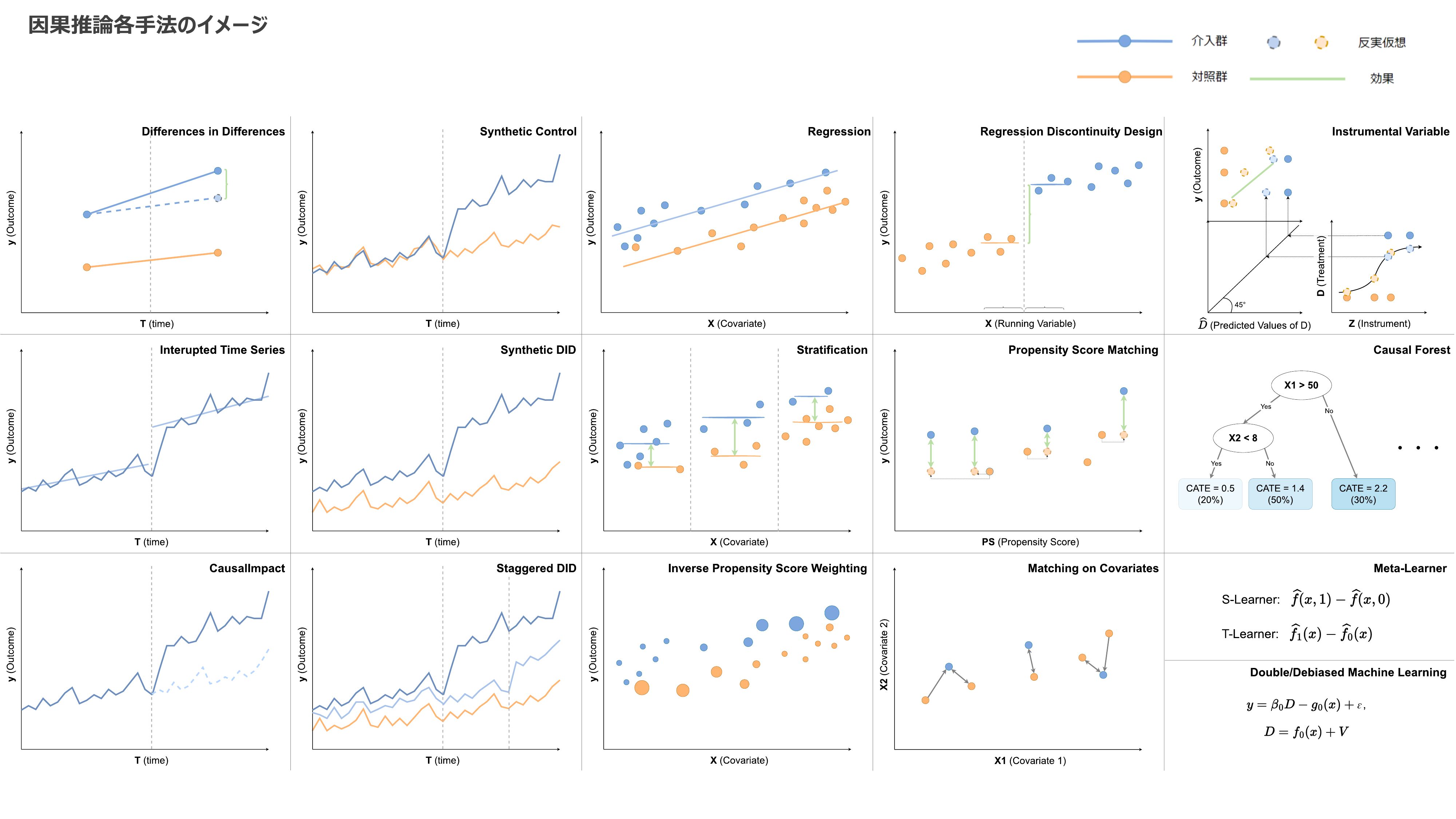
各手法の説明まとめ

page_3.png

  • あくまでざっくりイメージです。誤解を招く/分かりにくいなどあったらご指摘くださいmm
  • 詳細は以下の説明中に記載しています

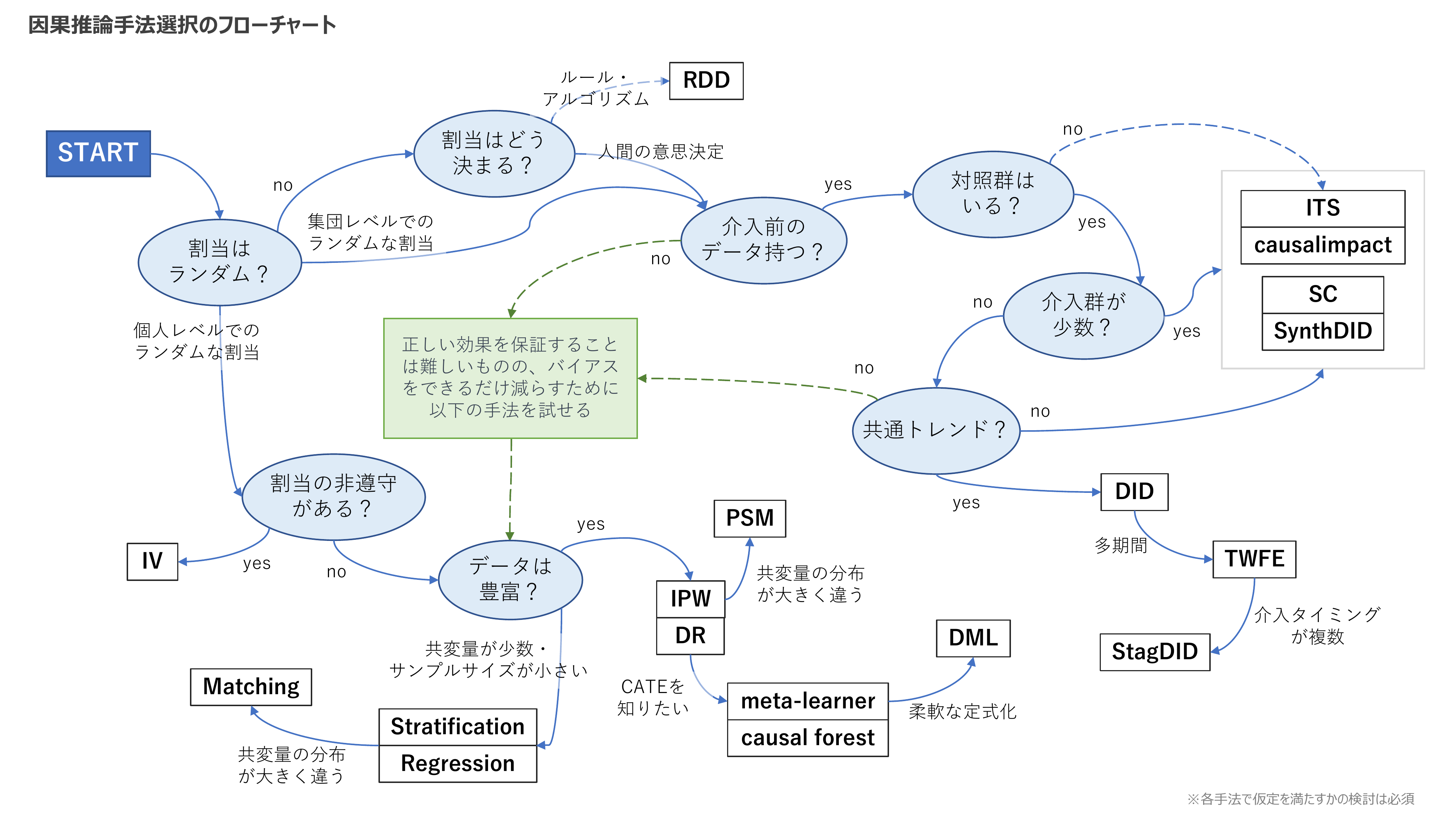
因果推論手法のマッピング

page_1.png

  • これに従った手法を使えばいいというものではありません
  • また、手法間の優劣をつけるという意味合いも持たないです
  • あくまで手法間の関係を整理するためのものとしてご笑覧ください

上図について、左上のSTARTから順を追ってひとつひとつ説明していきます。

方針

教科書的な定義に基づくと、「強く無視できる割り当て（CIA; Conditional independence assumption）2」が成り立つかを基準に考えるべきです。しかし、CIAはデータから証明することができない、かつ抽象的な仮定であり、それに基づいて考えるのは難易度が高いでしょう。

その代わりに、「割り当てにランダムネスがあるかどうか」を最初に考え、ランダムな割り当てがない場合はいわゆる自然実験の手法を優先するようにしています。

また、因果推論では第三者への説明性が重要なため、シンプルな手法を優先しています。

:white_check_mark: 割り当てはランダムか？

chart1

:arrow_right: 完全にランダムに割り当ててなくても、一部ランダムな要素が入った割り当てをしていれば、その変動を用いることができる

  • 例：MLモデルの予測確率にしたがって配信するかどうかを決める。0.4の人には40%の確率で、0.92の人には92%の確率でランダムに配信、という風に割り当てる
    • → 同じ特徴量を持つ人を比べると、配信されるかどうかはランダムに決まっている
  • 例：顧客セグメントごとに、ランダムに対象セグメントにするかどうかを決める

:arrow_right: ランダムの単位を考える

  • 個人単位の場合 → おそらく数が多いので、普通のABテストが出来ていると思って単純な比較でOK
    • 例えば時系列でみた時、介入前の介入/対照群の数字が一致するので、DIDを使う必要がない（介入後の比較で十分である）
    • 個人／集団での割り当てという分け方はあまり自明ではないので、この「介入前の比較で考える」のがひとつの指針になるか (データ見れば分かるし)
  • 集団単位の場合 → ランダムと言えど介入/対照群に差があるかもしれないので、介入前のデータも活用するDID的なアプローチを検討3
    • 例：ある地方のみを対象に広告を配信する
    • 例：適当に選んだ10店舗を対象に、新商品のテストを実施する

:white_check_mark: 割り当ての非遵守がある？

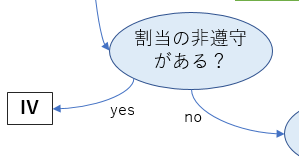
chart2

:arrow_right: 介入群に決めた人が、本当は介入を受けないケース（非遵守）がありうる。この場合介入群に介入を受けていない人も混ざっており、「介入を受けた／受けてない」軸で比較をしても、知りたい効果を見ることはできないため、操作変数法を用いる。

:arrow_right: 受ける資格があるかはランダムに決まっているが、個人が介入を受けるかどうかを決定する場合も含む

  • 例：薬を処方されたけど飲むのをやめてしまう
    • 処方対象をRCTで選んでいたとしても、「効果がなさそうだから飲まなくなる患者」がバイアスを生んでしまうため、薬の服用有無でその後の症状の単純比較をすることができない4

操作変数法（IV）

iv
  • 操作変数 (Z) の変動による介入の変動（= Zによる予測値）を用いることで、未観測の交絡を取り除く手法
    • 右下の領域で示した Z による D の予測値（薄い丸）を、左上の領域のように y に回帰する
  • 操作変数も介入もBinaryの場合、LATE（操作変数によって介入か否かが変わる人に対する平均効果）を推定している
    • ※上図は見やすさのためZを連続にしている
項目 詳細
estimand LATE
library (R) ivreg(vignettes, sem(reference))
library (Python) statsmodels(docs), linearmodels(github, docs), EconML(docs)
  • ビジネスでのIVの使いどころは、通知の例のように「資格がランダムに与えられる」ケースくらいだと思う。IV自体はもっと汎用性が高く、DeepIVのような応用的な手法もあるが、観測データにおいて仮定が成り立つと自信をもって言えるケースはそんなに多くはないと思う5
  • 介入ではなく操作変数による効果を推定するアプローチもある（ITT; intention to treat）
    • 実際に操作できるのは操作変数自体であり、効果検証後の活用まで考えてもITTが分かれば十分なことも多い

:white_check_mark: 割り当てはどう決まる？

chart3

:arrow_right: ランダムに決まっていなくても、ルールやアルゴリズムの閾値に応じて割り当てが決まっている場合、局所的なランダムネスを用いて効果を推定する手法が存在する。

  • ルールやアルゴリズムに基づいて決まっている場合
    • 境界付近は「ほぼ同じだけど介入の対象になったかだけ異なる」人たちなので、彼らを比較する、というアイデアを用いる（RDD）
    • 例：MLモデルのスコアが0.7以上の人を施策対象にする
      • スコアが0.69の人と0.71の人では、施策の対象になる以外の違いは無視できると想定する
    • 例：前月の総支払額1000円以上に人を対象にクーポンを送る
  • 人間が決めている場合
    • 手を上げる方式
      • 効果が大きい人から挙手するバイアスがかかりがちなことに注意
    • 誰かが選ぶ方式
      • 効果が大きそうな人から選ぶバイアスがかかりがちことに注意

回帰不連続デザイン（RDD）

regression-discontinuity
  • 境界を超えるかどうかで介入の有無が決まるケースで、境界付近の人達を比較する
  • 条件に当てはまるための操作ができないことが必要
    • 例：「今月の総支払額1000円以上に人を対象にクーポンを送付」と事前に言ってしまうと、クーポン受け取るために購入額を増やす人がいるのでNG（境界上下の比較がフェアにならない）
項目 詳細
estimand LATE
library (R) rddtools(github, vignettes), rdd(cran)
library (Python) rdd(github)
  • estimandはLATEであり、あくまで境界付近の効果しか分からないことに注意
  • なお、成田悠輔らは「アルゴリズムは実験」である、つまり、アルゴリズムによる意思決定に対してRDDを拡張・一般化した手法を用いることで、因果推論が広く可能になる世界が来ていると主張しており、とても熱い：https://www.rieti.go.jp/jp/publications/nts/21e057.html

:white_check_mark: 施策前のデータを持つか？

chart4

:arrow_right: 時系列のデータを用いることで、大雑把に言うと

  • 「似ている」対象間の比較のハードルが下がる
  • 動的な効果を推定できる

という２つのメリットがある。

フローチャートだと少し後に出てくるが、DIDが最も基本的な手法になるのでそちらから紹介する。

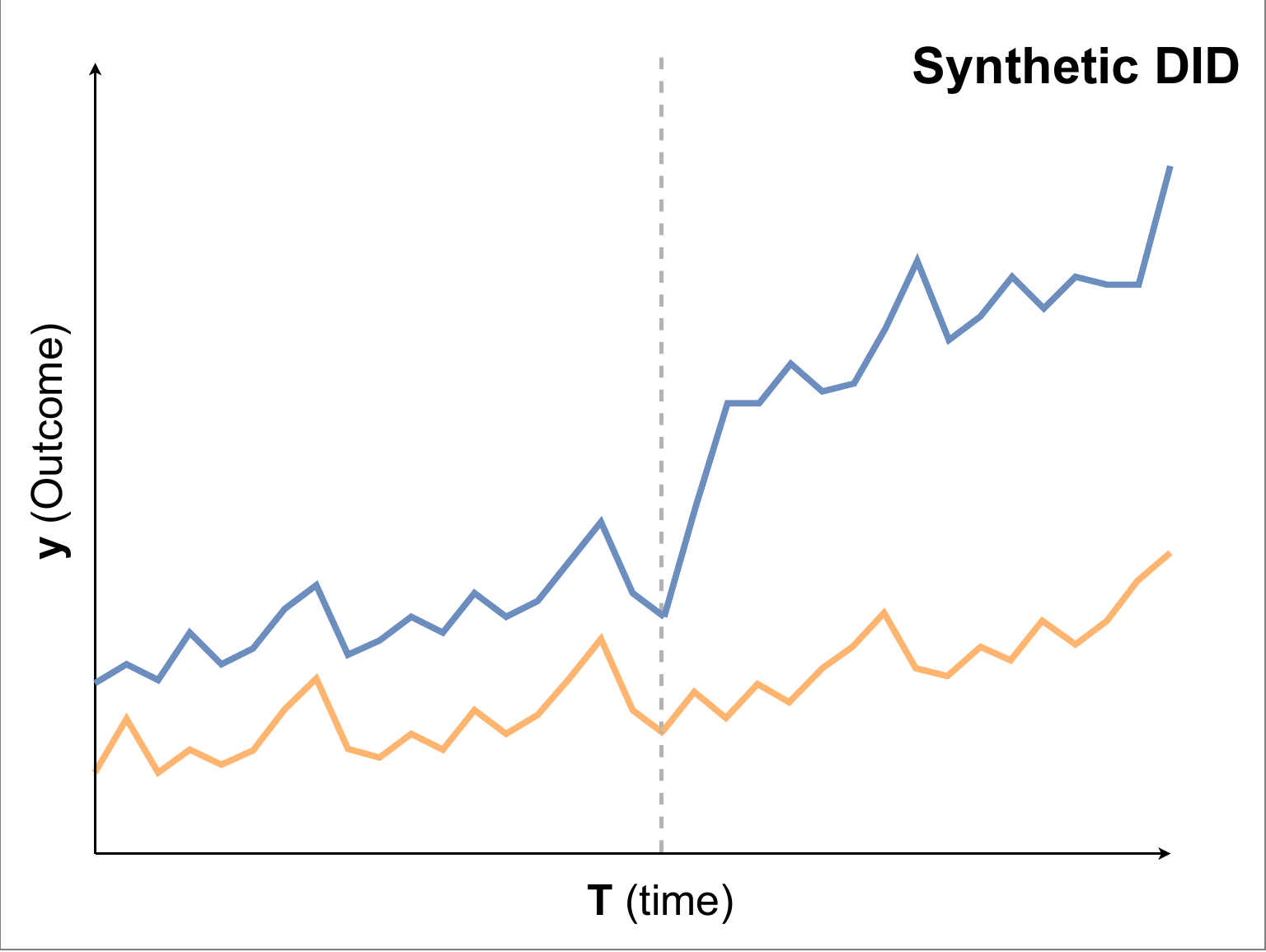
差分の差分法（DID）

diff-in-diff
  • 上の図で、薄い青丸（介入を受けた人が介入を受けなかったであろうときの反実仮想的なOutcome）と実際の数値の差分が因果効果だと推定する手法
  • 共通トレンド
    • 介入を受けた人が受けなかったときの経時変化（トレンド）は、介入を受けなかった人が実際に経験した経時変化と同じだという仮定
項目 詳細
estimand ATT
library (R) lmを使用する
library (Python) statsmodelsを使用する
Pythonで因果推論(9)~差分の差分法(DID)による効果検証~

:white_check_mark: 介入群、対照群の数は少数か？

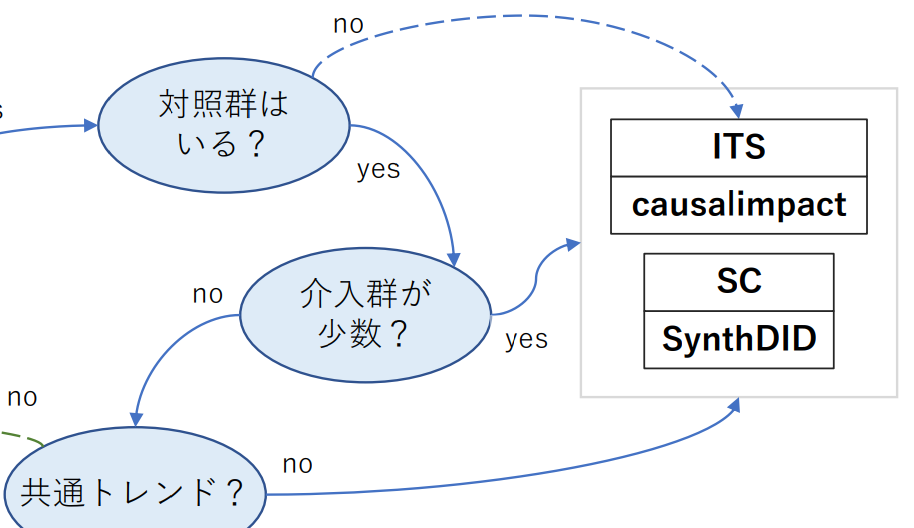
chart5
  • 対照群がない場合
    • 過去のデータから時系列予測したものと、介入実施後の実際のデータを比較する手法を用いる（CausalImpactあるいは少しニュアンスは違うがITS）
    • が、妥当な時系列予測ができるという仮定はやや厳しい。特に同時に行われた別の施策やイベントの影響を除くことは基本的には不可能
    • 例：全国一斉の販促キャンペーンの効果を知りたい
  • 介入群が少数の場合
    • 比較可能な対象を上手いこと「合成」する手法を用いる（SC、SynthDID）
    • CausalImpactも使える。むしろ対照群のデータがあることで初めて時系列予測の精度が妥当になるケースも多い
    • 例：全国50店舗のなかで、1店舗にだけトライアルで施策を行った結果を測りたい
  • 介入群・対照群ともに多数ある場合
    • CausalImpactは単一の時系列を対象にした手法なため、介入群が複数あるパネルデータの場合の扱いは定かではない。単純に平均値や合計値に対して使っていいものかは非自明6
    • 共通トレンドが成り立つ場合、SC、SynthDIDもやる必要性は薄い（シンプルなDIDで十分）

分割時系列デザイン（ITS）

interrupted-time-series

CausalImpact

causalimpact
  • 過去のデータ＋介入から影響を受けない共変量（対照群のデータ含む）を用いて、介入が起きなかった場合の反実仮想の系列（点線）を予測する
  • 実際に観測されたデータと反実仮想との差分を効果とみなす
項目 詳細
estimand ATT
R causalimpact(github, vignettes)
Python tfcausalimpact(github), causalimpact(github)7

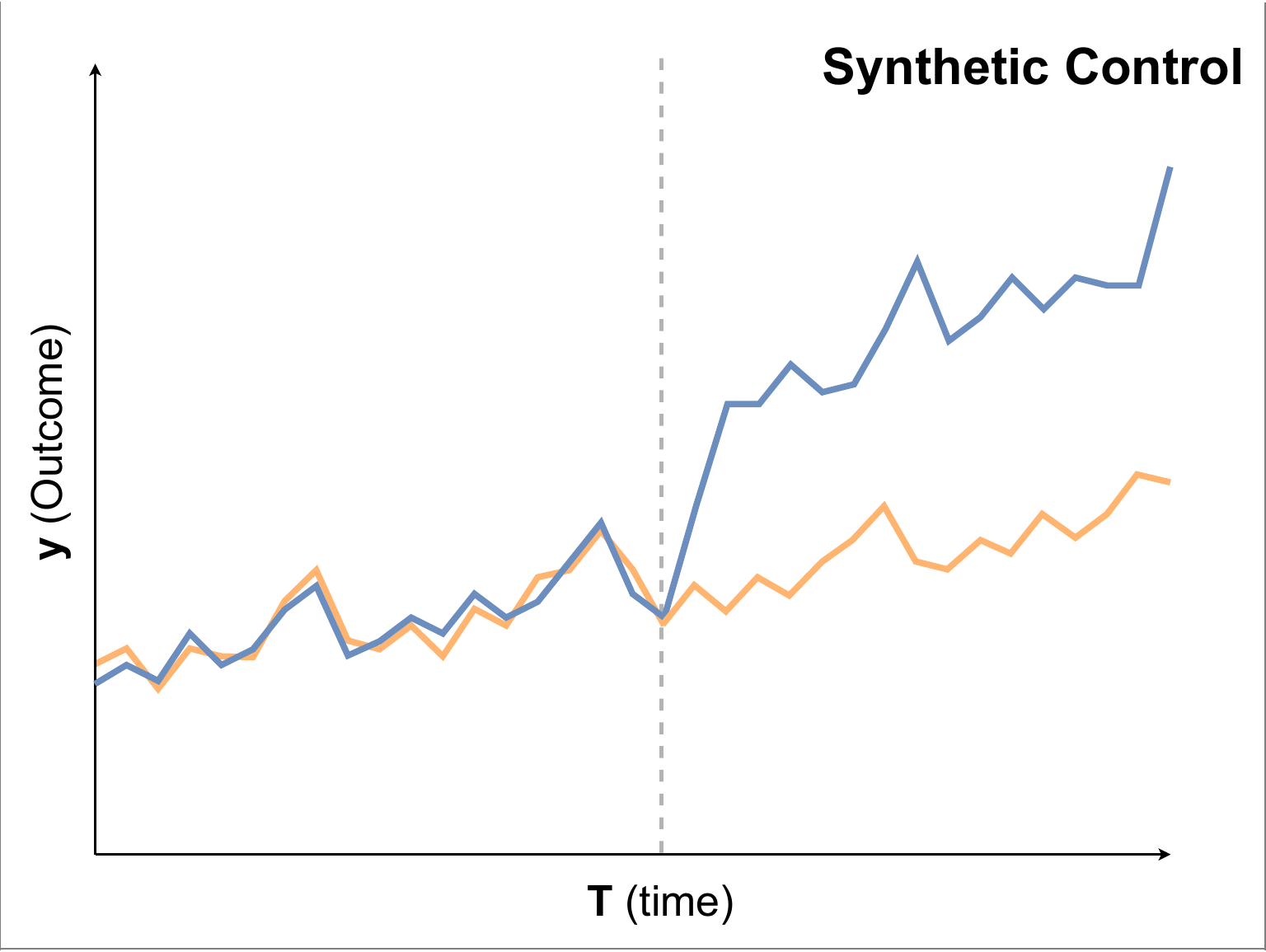
合成コントロール（SC）, 合成DID（Synthetic DID）

synthetic-control synthetic-did

  • Synthetic Control：介入以前のデータが同じ動きになるように、対照群の中からサンプルを選んで重みづけすることで仮想的な対照系列（オレンジ）を作成する
  • Synthetic DID：介入以前のデータが平行な動きをするように、対照群の中からサンプルを選んで重みづけすることで仮想的な対照系列（オレンジ）を作成する
項目 SC Synthetic DID
estimand ATT ATT
R tidysynth(github), Synth(hp, reference) synthdid(docs)
Python SyntheticControlMethods(github) pysynthdid(github), synthdid(github)

:white_check_mark: 共通トレンドを持つ場合の拡張

chart6
  • 多期間への拡張
    • 検出力UPおよび、動的な効果の推定
  • 介入タイミングが複数ある場合
    • 複数の介入タイミングがあることに由来するバイアスがありうる（→ Staggerd DID）
      • 学術的にはここ数年ホットなトピック（落ち着いてきたらしいので、今後はビジネスでも使われる機会増えるはず）

Staggered DID

staggered-did
  • 介入タイミングが複数ある場合に用いる手法
    • かなり多くの手法が提案されているため詳細は割愛
  • 日本語ではこれらで読める

項目 詳細
estimand ATTなど
R fixest(docs) など
Python -

:white_check_mark: ランダムネスがないとき、DIDが使えないとき

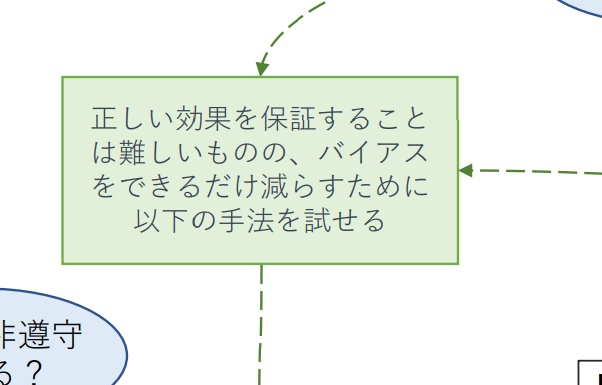
chart7

:arrow_right: ここにたどり着いた状況だと、おそらくCIAの仮定が満たされると（つまり、正確な効果の測定を）強く主張することがなかなか難しいケースも多い
:arrow_right: が、何もしないないよりは少しでもバイアスを取り除きたいという意思で以降をやることになる。ちなみにEBPMのエビデンスレベルの考え方でDIDが優先されてたため、こっちが劣後するようなフローにしている8

:white_check_mark: データは豊富か？

chart8

回帰分析 （Regression）

regression
  • 交絡を全て入れて回帰を行えば、因果効果を識別できる
  • ランダム化比較試験が行えている場合でも、共変量を入れて回帰を行うことで推定量の正確性は向上する9

層別集計（Stratification）

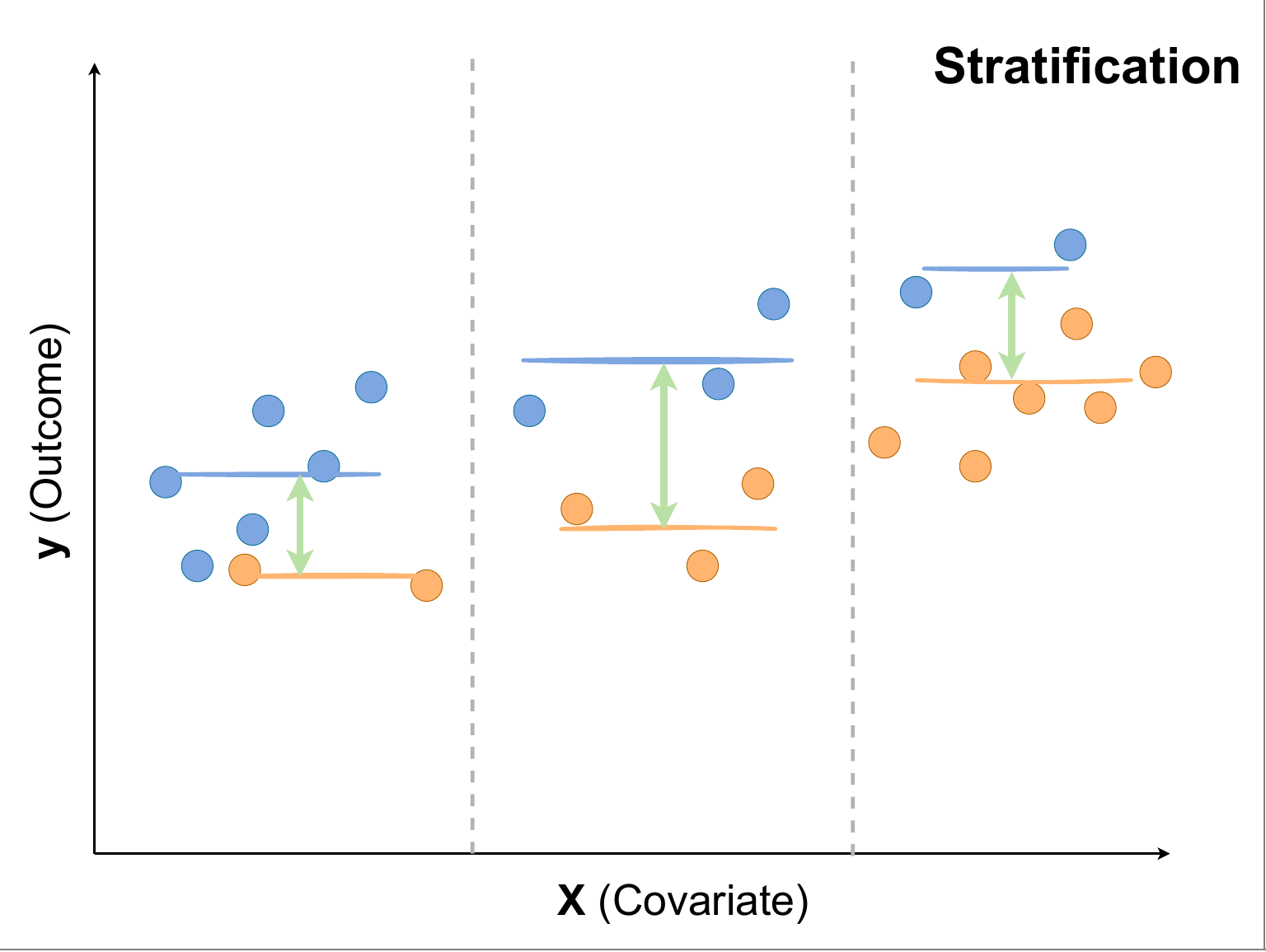
stratified
  • 割り当てがある特定の変数と強く相関して決まっている場合、その変数の値別に介入/対照群を比較することで、効果を確認する
    • 上図において、全体の平均は介入/対照群で大きく違いはないが、Xの値で切ってみると介入群（青）のほうがOutcomeが大きいことを確認できる
    • 軸として用いるべき変数の考え方は、共変量の入れ方と同じで良い
  • 交絡変数が多くある場合は、ひとつの軸で切っただけでは捉えきれないバイアスが残ってしまう
項目 Stratification, Regression
estimand CATE
R - （※シンプルな手法のため、lm などで記述可能）
Python - （※シンプルな手法のため、statsmodelsなどで記述可能）

逆確率重み付け法（IPW）, Doubly Robust

ipw
  • IPW：介入群については介入されにくい（介入されるサンプルが比較的少ない）人を重み大きくつけ、対照群については介入されやすい（介入されないサンプルが比較的少ない）人に重みを大きくつける
    • 上図の円の大きさが重みを表すイメージ
    • 逆確率をかけるため、介入確率が低い（オレンジが密集している）右側のサンプルに対して、介入群（青）の重みを大きくしている
  • DR：IPWと回帰を組み合わせた手法
  • 傾向スコアを用いることで、次元が高い共変量を圧縮して1次元として利用することが可能となる
項目 IPW DR
estimand ATE ATE
R PSWeight(vignettes), weightit(docs) drtmle(vignettes)
Python causallib(docs), DoWhy(docs) 同右

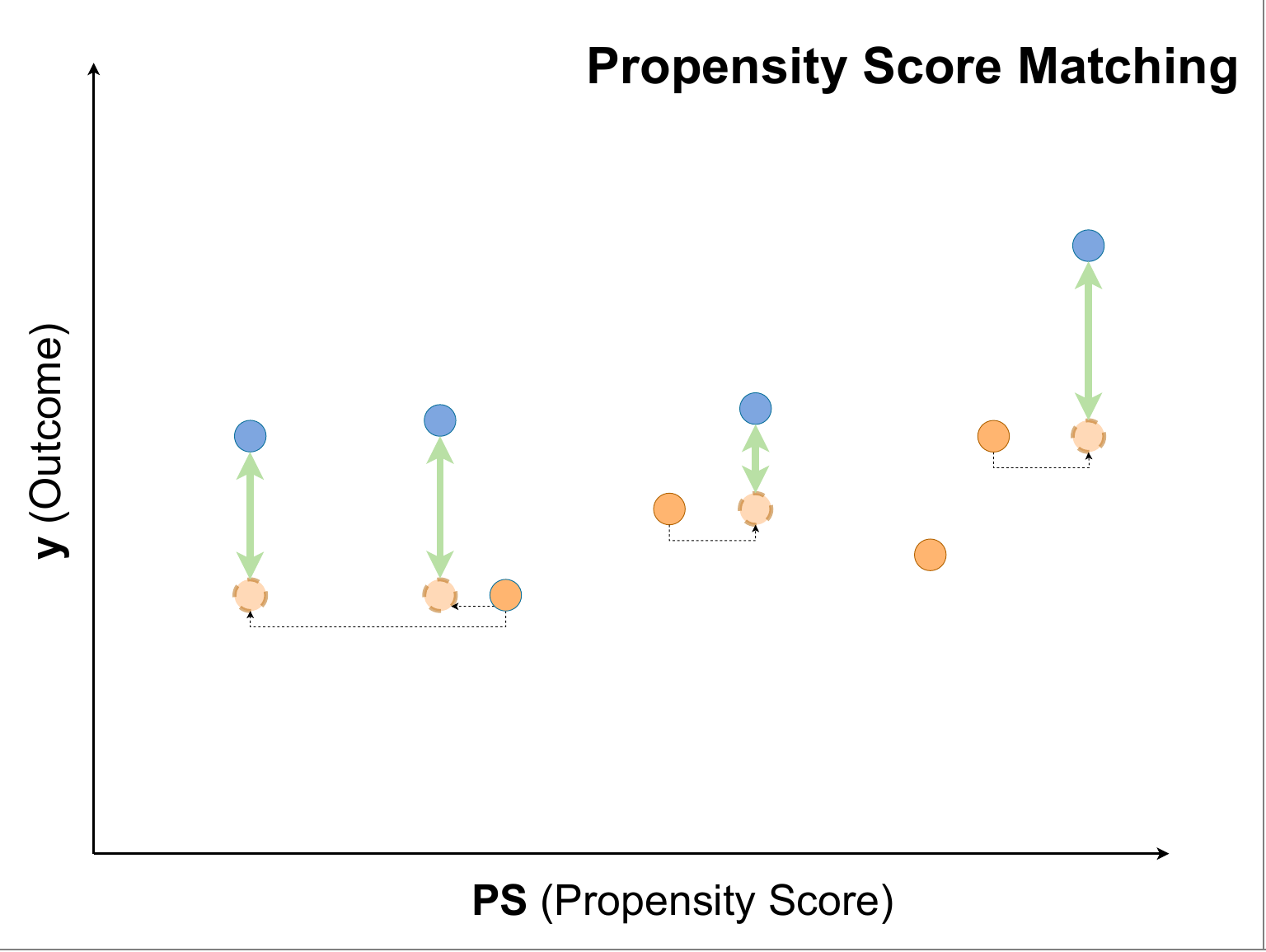
マッチング、傾向スコアマッチング（PSM）

psm matching

:arrow_right: 自身と反対の群に割り当てられているなかで、似ている人を特定し、その人と比較するアプローチ

  • PSM：傾向スコアを用いてマッチングする（左）
    • 図はATTを求めるために、介入群のサンプルと似ている対照群をマッチングをしている
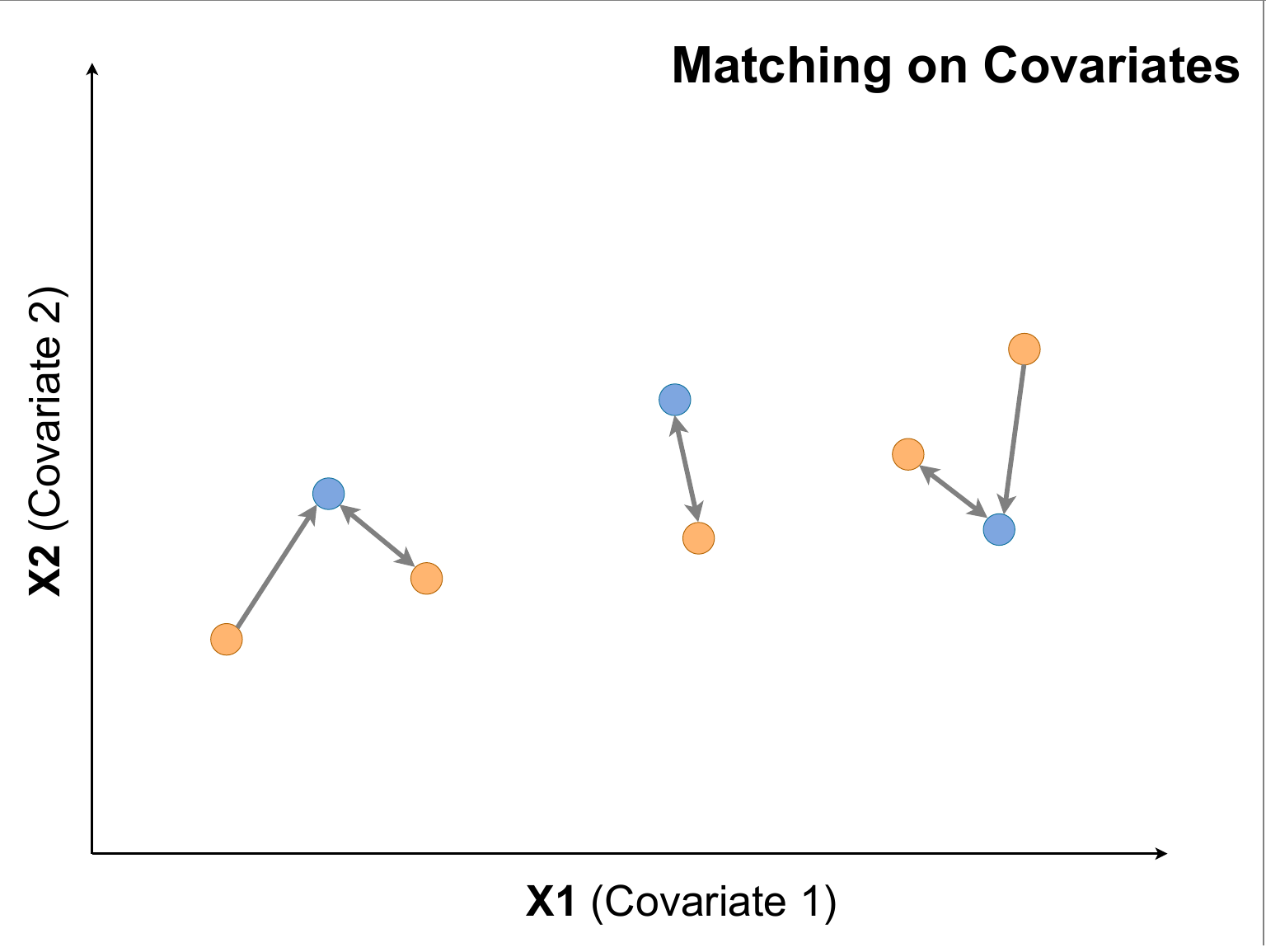
  • matching on covariates：共変量を直接用いてマッチングする（右）
    • 図はATEを求めるために、サンプルと似ている違う群をマッチングしてる
項目 Matching PSM
estimand ATEなど ATEなど
R matchit(docs, vignettes) 同右
Python causallib(docs), DoWhy(docs) 同右, psmpy(pypi)

:white_check_mark: CATEを知りたい？

chart910

:arrow_right: 施策対象として効果がある人を抽出したり、パーソナライズした施策を行う際には、CATEを知る必要がある

  • 例：Uplift modeling
  • CFML (counterfactual machine learning) は、このあたりの手法を指すことが多い

:arrow_right: ただし、moderationは基本的にどの手法でも入れられるため、他の手法でCATEが算出できない訳ではない

  • moderation：D → y の効果が X によってどう変わるか11
  • 本記事で紹介する多くの手法は回帰の形で書けるので、DとXの交差項を入れればmoderationが分かる

Meta-Learner

meta-learner
  • 任意の予測モデルを用いて、予測値の違いを用いてCATEを推定する
    • S-Learner: ある予測モデルに対して、介入した場合の予測値（$f(x, 1)$）と介入しなかった場合の予測値（$f(x, 0)$）のそれぞれを求め、その差分を効果とする
    • T-Learner: 介入群のみで学習した予測モデルの予測値（$f_1(x)$）と、対照群のみで学習した予測モデルの予測値（$f_0(x)$）をそれぞれ求め、その差分を効果とする
項目 詳細
estimand CATE
R cre
Python EconML(docs), Causal ML(docs), causallib(docs)
  • ATEとかATTだけ知れれば十分な場合に脳死でmeta-learnerをやる必要性は個人的にはあまり感じない
    • 特に時系列構造を持つ場合（＝ビジネスのほとんどのケース）では共変量の入れ方とかで事故る可能性があるので、理解した上でmeta-learner使うのが好ましい。このあたりもDID系が優先されるようなフローにしてる理由だったりする
    • 統計学を使う分野の出身でないデータサイエンティストやアナリストに一番なじみやすいのがmeta-learnerなのはその通りなので、上手いこと使いたい

causal forest

causal-forest
  • causal treeを拡張したもの
  • 統計的推測もできるのが嬉しい
項目 詳細
estimand ATE
R grf(docs)
Python EconML(docs)

:white_check_mark: 柔軟な定式化

chart10

:arrow_right: 関数形を指定したり、部分的にMLを活用するようなケース

  • 例：予測モデルを使った数理最適化としてLPやQPに落とし込むために、モデリングの柔軟性は保ちつつも効果の項は線形にしたい12

:arrow_right: （本記事では取り扱わないが、）連続な介入のときに力を発揮するイメージ

Double/Debiased Machine Learning（DML）

dml
  • 一部線形モデルで一部は機械学習から成る、PLR（部分線形回帰）を推定できる
  • 統計学と機械学習のintersection的な手法で萌えるが、ここで力尽きたので説明は割愛します。すいません。。
項目 詳細
estimand ATE
R DoubleML(docs)
Python EconML(docs), DoubleML(docs)

最後に

因果推論の各手法のイメージ、いつそれらを使うべきかについて紹介しました。実際に効果検証をする際には、「何を使うか」よりも 「各手法の仮定は成り立つか？」「知りたい効果はそれでいいのか？」「それを知ってどうするのか？」 という本質的な問いに割く時間を増やせるとみんなハッピーになると思います。本記事が手法のテクニカルな部分の摩擦を減らす一助になれば幸いです。

参考

各手法の参考をあげだすと膨大になってしまうので、フローチャートを作る際に参考にした記事を紹介します。

※ 絵はgithubにpdfでも上げています

  1. 各手法の詳細については、記事内で多めにリンクを貼っているので、そちらをご参照ください。なお、ググったら日本語の記事がヒットする手法を中心に紹介しているつもりです。 ↩

  2. 定義や扱いの微妙な違いはあるが、分野によってunconfoundedness, ignorability, conditional independence, selection on the observables, no omitted variable bias, exogeneity, exchangeabilityなどとも呼ばれる (https://dspace.mit.edu/bitstream/handle/1721.1/85887/attribution-ajps.pdf?sequence=1&isAllowed=y ) ↩

  3. 「マーケティングデータ分析で成果を挙げるには「統計分析（MMMなど）＋A/Bテスト」のコンビネーションが有用 - 渋谷駅前で働くデータサイエンティストのブログ」などでも言われてる ↩

  4. https://stat-expert.ism.ac.jp/wp/wp-content/uploads/2023/02/SSE-DP-2022-3.pdf ↩

  5. ランダムでなくても、ある仮定（計量経済学の言葉を使うと関連性と外生性）を満たすような変数 Z は操作変数として用いることができる。しかし、たとえば「LINEギフトの初めての受け取りがその後の利用に与える影響」で扱っているように、関連性が弱い "Week IV" などへの対処は煩雑である。一方で「モバイルクーポンと非計画購買：操作変数法を用いた効果測定 - 田頭拓己のブログ」のような芸術点が高い操作変数もあるのがたまらない。ちなみに研究では "Shift-Share Instrment" といった広く応用できそうなアプローチも出てきているので、今後は役割が広がっていくかもしれない。なお、Pearlらの『因果推論の科学』では、DIDがIVとして紹介されているので、そう意識していないけど「IVと解釈できるもの」は色々あるのかもしれない。 ↩

  6. 少なくともGoogle製のRライブラリはその仕様になっている。この件については https://qiita.com/Gotoubun_taiwan/items/49c72820ae0b771f5500 や https://stats.stackexchange.com/questions/176577/causalimpact-with-panel-data などでも指摘されている。一方でCausalImpactのもとになっているBSTS自体は柔軟なモデリングができるはずなので、拡張は出来るような気もする。 ↩

  7. CausalImpactは実装によって中身に重大な差異がある - 渋谷駅前で働くデータサイエンティストのブログ ↩

  8. https://www.murc.jp/wp-content/uploads/2022/10/seiken_160212.pdf の図2など ↩

  9. 例えば『インベンス・ルービン 統計的因果推論 (上)』の7.5節を参照 ↩

  10. このフローチャートでは IPW/DR から矢印を伸ばしているが、別にRegressionあたりから伸びていてもなんら問題はない。一応データがリッチなときにCATEを詳細に知りたいであろう点を考慮してこちらから引いている。 ↩

  11. https://en.wikipedia.org/wiki/Moderation_(statistics) ↩

  12. https://www.jstage.jst.go.jp/article/bplus/12/1/12_46/_pdf のようなケースで用いることができる ↩

150
153
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
150
153