機械学習を用いた因果推論
近年盛んにおこなわれている機械学習の手法を用いた因果推論についていつ利用するかの大まかな理解とメモ(備忘録)
基本的には現在の因果推論手法のフローチャート的まとめ
はじめに
因果推論とは、結果に対する原因を答えることを目的とした一連の統計的手法である。一般に回帰分析などの統計的アプローチでは、Xの変化がYの変化とどのように関連しているかを定量化することに重きをおいている。一方で統計的因果推論は、Xの変化がYの変化を引き起こすかどうかを判断し、この因果関係を定量化することに重きをおいている。近年盛んである機械学習と因果推論の融合分野は、このうち特定の条件下における因果効果の推定に用いられる。今回は既存の因果推論の手法と機械学習を用いた手法の使い分けを大まかに整理した。
当然だが有するデータに対して「何を、なぜ知りたいか?」を明確にしてから分析していく。
でないと、取るべき戦術が見えてこない。
因果推論の一般的戦術
因果推論は様々な方針が取られている。そのため自身が有するデータから因果推論をおこなうには様々な方法が考えられる。まずは因果推論を構造的に理解するために、2つのカテゴリーに分ける。今回は有するデータが実験データか、または観測データかを識別し、それぞれで代表的なアプローチをみていく。
方針
- 実験データか観測データかの識別
- 実験データでの因果推論
- 観測データでの因果推論
実験データでの因果推論
実験データの場合、因果効果の検証のために実験がデザインされているため、推定は観測データに比べて明確でわかりやすい。多くの場合はRCT(Randomized Controlled Trial)条件に近づけるように解析をしていく。ただし、あくまでもデザインされた実験中の平均的な因果効果の推定では、古典的な統計的因果推論の手法を用いることで推定をすることができる。しかしながら、平均的な因果効果だけでなく、特定の状況や条件下での因果効果について推定したい場合がある。そこで、近年では機械学習の手法を織り交ぜた因果推論によりそれを可能にしている。
実験データでは大きく4つのカテゴリーに分けて考えていく。
- 介入と非介入との共変量の差異
- 介入グループの一部が非介入
- 介入グループの中でサブグループごとに効果が異なる
- 因果関係の構造的把握
有するデータが実験データと判断されたら、上から順に考えていく。そして目的の分析を実行する。
介入と非介入との共変量の差異
一般的な因果推論である。基本的には介入グループと非介入グループ間での因果効果を推定したい場合を想定している。その時、処置(原因)と応答(結果)以外の共変量がグループ間で異なってしまう。すると正しい効果を推定することができなくなってしまう。そこで、この共変量をグループ間で出来るだけ等しくなるように調整して、その上で推定していく。主な方針としてDIDやマッチング、IPWなどが挙げられる。
→ DID・マッチング・IPW etc.
介入グループの一部が非介入
実験研究において介入効果に偏りのない推定のため、介入をランダムに割り付けたとしても、この介入が必ずしもその通りに実行されるとは限らない(ノンコンプライアンス)。介入の割り付けと実際に受けた介入とが等しければ、個体は割り付けられた介入を遵守したことになる。一方、等しくないときはノンコンプライアンスとなる。つまり、ノンコンプライアンス条件下では介入グループは、遵守グループと非遵守グループとで異なるグループが混在することになる。よって、遵守グループに限定した平均因果効果を推定する必要がある(LATE)。
→ 操作変数(IV)
介入グループの中でサブグループごとに効果が異なる
介入グループの中でもサンプルごとにそれぞれ異なる共変量を取っている。そして、特定のサンプルごとに介入効果を求めるとき、介入グループの中でも特定の条件でPersonalizeされた介入効果を計算する必要がある。いわゆる機械学習を用いた因果推論。
→ HTE(Heterogeneous Treatment Effects)、Uplift Modeling
→ GRF(Generalized Random Forest)、ORF(Orthogonal Random Forest)は傾向スコアを算出せず介入効果を推定
→ Meta-Learnerはグループごとにモデリング&効果推定後、傾向スコアを用いてその推定値から介入効果を推定
因果関係の構造的把握
ある変数が別の変数に影響を与える場合、直接作用する場合と媒介変数を通じて間接的に作用する場合とがある。このとき、変数間で影響する効果のうち、どの程度直接的で、どの程度間接的であるかを分析することは重要である。この原因と結果の関係だけでなく結果の原因となったメカニズムを理解することによって、どの媒介変数を変化させれば高い効果が見込めるかを分析することが可能になる。
→ 媒介分析
観察データでの因果推論
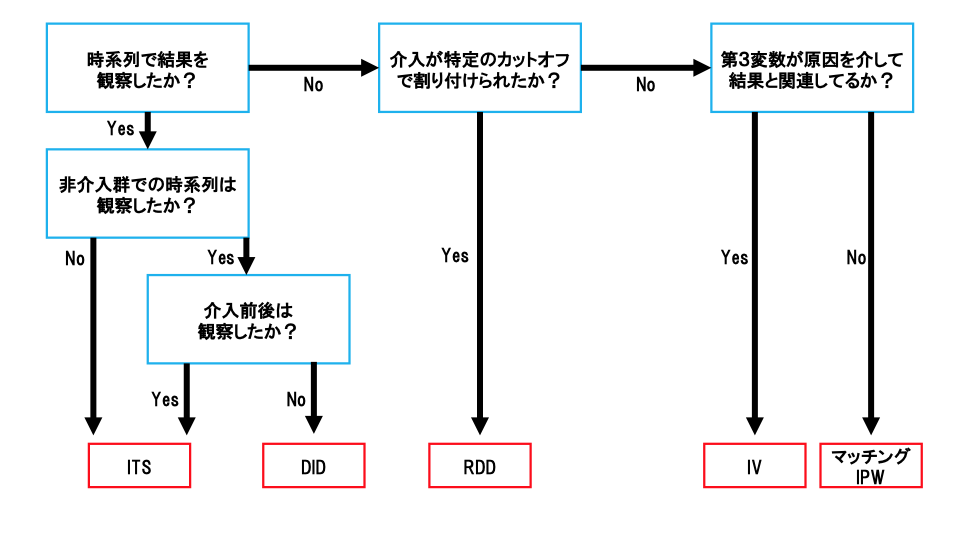
観察データの場合、定期的に観測されるものが多い。その際、時系列データとして利用することになる。一方、時系列データでない場合は原因および結果となる変数以外の変数を定義することになる。このとき、特定の状況に関する十分な知識が必要となる。これを基に因果構造を決定していく必要がある。
観察データでは以下のように場合分けする。
Heterogeneous Treatment Effects (HTE)
個人は、バックグラウンドの特徴だけでなく、特定の治療、介入、または刺激に対する反応も異なる。特に、治療効果は治療の傾向によって系統的に変化する可能性がある(Xie et al., 2012)。そしてこの影響の不均一性が存在する場合、主な影響を用いた古典的な因果推論のアプローチであるAverage Treatment Effect(ATE)の推定では、必ずしも十分な推定がおこなえなかった。そこでバックグラウンドといったPersonalなレベルでの影響を加味した介入効果の推定としてHeterogeneous Treatment Effects(HTE)を考えることで、このそれぞれの影響を加味した推定が可能になる。その際、機械学習を用いて因果推論を実行していく。
HTEでの分析
RやPythonにライブラリやパッケージが存在する。代表的なものは以下。
R
・grf
・uplift
・rlearner
Python
・EconML
・CausalML
・pylift
参照
・ノーベル経済学賞でも注目の因果推論を俯瞰する
https://note.com/tak1/n/nf35b48502339
・Using Causal Inference to Improve the Uber User Experience
https://eng.uber.com/causal-inference-at-uber/
・X-Learnerについて調べた内容のまとめ
https://dev.classmethod.jp/articles/causal-metalearner-xlearner/
・EconMLパッケージの紹介 (meta-learners編)
https://usaito.hatenablog.com/entry/2019/04/07/205756
・Yu Xie, Jennie E. Brand, and Ben Jann. (2012) Estimating Heterogeneous Treatment Effects with Observational Data. Sociol Methodol 42(1): 314-347.