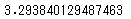はじめに
マーケティング施策が実際に効果があったか因果関係を推論したい場合は、介入を行うのが好ましいです。例えば、プッシュ通知を送るなど施策を実施する人達と実施しない人達に分けて、それぞれのグループの売り上げを比較することで、プッシュ通知というマーケティング施策に効果があるかを検証します。
しかし、プッシュ通知を送っても、スマホのバージョンが古いなどによって、プッシュ通知が届かない可能性があります。このようにマーケティング実施者の割り当てと、顧客に起こる事象が異なる場合があります。これを「不服従(ノンコンプライアンス)」と言います。
この不服従があると、プッシュ通知を送ったグループと送らなかったグループの売り上げを比較しても、施策の効果を検証できない可能性があります。スマホのバージョンが古くてプッシュ通知が届かない例の場合、スマホのバージョンが古い人は年収が低い可能性があります。
不服従がある場合に因果効果を推定する方法として、操作変数法があります。この記事では、操作変数法の概要、操作変数法が使える条件、pythonのlinearmodelsを使った操作変数法の実装を取り上げます。
因果推論での操作変数法
4つのグループ
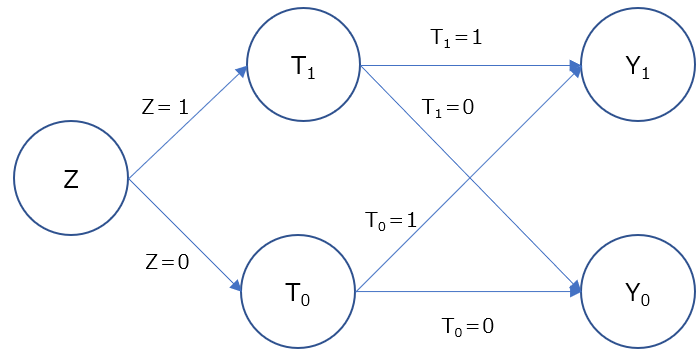
調査対象の人には、以下の4種類の人がいるとします。
| 分類 | 操作変数$Z=1$のとき | 操作変数$Z=0$のとき |
|---|---|---|
| Complier | 説明変数$T_1=1$ | 説明変数$T_0=0$ |
| Never-taker | 説明変数$T_1=0$ | 説明変数$T_0=0$ |
| Always-taker | 説明変数$T_1=1$ | 説明変数$T_0=1$ |
| Defier | 説明変数$T_1=0$ | 説明変数$T_0=1$ |
新薬の治験の場合だと、Never-takerは新薬を渡されても飲みません。一方でAlways-takerは頼まれてもいないのに新薬を飲もうとします。Defierは新薬を渡されたら飲まず、頼まれていない場合は新薬を飲もうとするひねくれ者です。
Complier以外の人がいる場合、操作で介入群($Z=1$)と対照群($Z=0$)に分けても、興味ある説明変数は別の行動を取る人が出て、以下のデータが得られることになります。
| ZとTの組み合わせ | 行動を取る人 |
|---|---|
| Z=1, T=1 | Complier, Always Taker |
| Z=0, T=0 | Complier, Never-Taker |
| Z=1, T=0 | Never-Taker, Defier |
| Z=0, T=1 | Always-Taker, Defier |
下2つが、こちらが意図した通りにの行動をしてくれない不服従な人です。不服従な人は、年齢や性別等の属性や、行動パターンがほかのグループとは異なる可能性が考えられます。この場合、下2つの行動を取る人には偏りがあることになり、因果推論は難しくなることが想像できます。
プッシュ通知での例
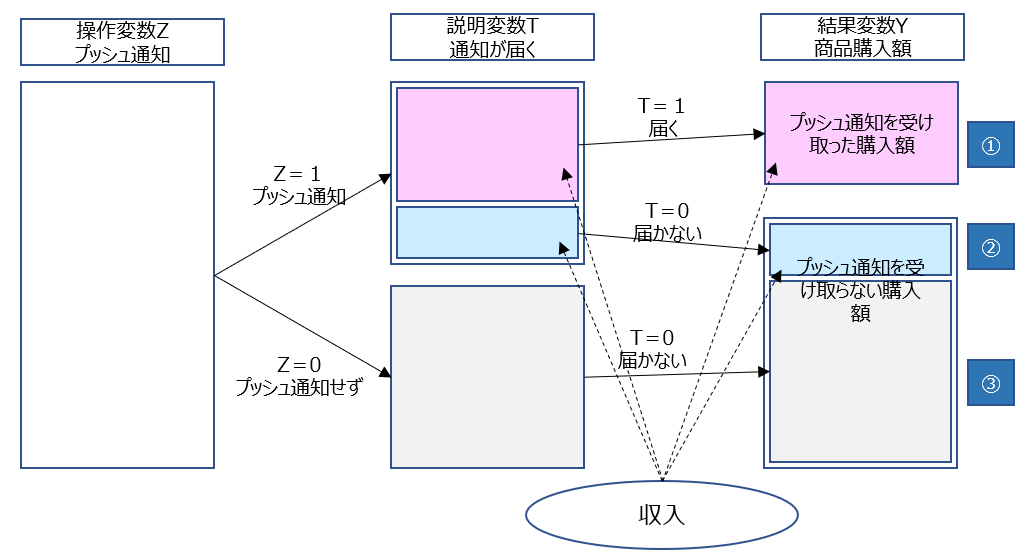
マーケティング施策としてプッシュ通知を送信する場合を考えます。操作としては、プッシュ通知を送る介入群と、プッシュ通知を送らない対照群に分けます。ただし、古いバージョンのスマホにはプッシュ通知が届かない場合を考えます。この場合、プッシュ通知を送った介入群の中でも、プッシュ通知を受け取れない人がいます(下図の②)。そして、古いバージョンのスマホを使っている人は、年収が少ない可能性があります。つまり、年収が交絡因子として存在します。そして、年収の情報が手に入らない場合は、この交絡因子を調整することができません。
プッシュ通知を送ったグループと送らなかったグループで購入量を比較する、つまり
E[Y|Z=1] - E[Y|Z=0]
を求めるとどうなるでしょうか。プッシュ通知を送った人の中には、プッシュ通知が届かなかった人がいます(②)。ですから、プッシュ通知によるマーケティングの効果を過小評価してしまいます。
また、
E[Y|T=1] - E[Y|T=0]
を求めるとどうなるでしょうか?$T=1$の人は年収が高い人たちにバイアスがかかっている可能性があります。このため、この推定量ではプッシュ通知の効果を過大評価してしまうと考えられます。
LATE
操作変数法を用いて、次の推定量を求めると、プッシュ通知によって購入量が増えたかを検証することができます。
LATE = \frac{ E[Y|Z=1] - E[Y|Z=0] }{E[T|Z=1] - E[T|Z=0]}
証明は省略しますが(証明を知りたい方は参考[1]などを参照)、結果だけを示すと $LATE$ は以下のようになります。
LATE = E[Y_1 - Y_0 | T_1=1, T_0 = 0]
$T_1=1, T_0 = 0$ 、つまり Complier という条件付き で、プッシュ通知が送られた時の購入量$Y_1$とプッシュ通知が送られなかった時の購入量$Y_0$の差の期待値となります。
ただし、これが成り立つためには、以下の条件が必要です。
- $Z$と$T_1$, $T_0$, $Y_1$, $Y_0$は独立。つまり、操作$Z$はランダムに行われている。
- $T_1 = 0$ だが、$T_0=1$となる人、つまりDefierは存在しない。
2番目の仮定は、時には強い仮定となるかもしれません。プッシュ通知では、こちらからプッシュ通知を送っていないのに、客が無理やり自分のスマホにプッシュ通知が届くようにすることはまず不可能なので、この仮定は成り立つと考えられます。2番目の仮定が成り立っているか、操作変数法で因果推論するときは重要になります。
サンプルデータ
こちらのプッシュ通知に関するサンプルデータを使います。
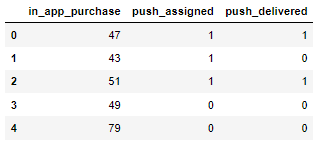
以下の3つのカラムが入っているデータです。
| カラム | 説明 |
|---|---|
| in_app_purchase | アプリ内での購入額 |
| push_assigned | プッシュ通知を送れば1、送らなければ0 (操作変数$Z$) |
| push_delivered | プッシュ通知が届けば1、届かなければ0 (説明変数$T$) |
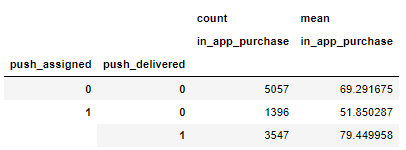
push_assigned, push_deliveredの値ごとに、件数とアプリ内購入額平均値を求めた結果です。
10000万人中、1396人はプッシュ通知を送るグループに割り当てられたものの、プッシュ通知が届いていません。
$E[Y|Z=1] - E[Y|Z=0]$を求めるため、push_assigned=1,0ごとのアプリ内購入額の平均を求めます。

71.7 - 69.3 =2.4 となりますが、上述の通り、これは過小評価されている可能性があります。
Pythonで操作変数法を実装する
初めに、pandasのデータフレームとして読み込んでおきます。
df = pd.read_csv('./input/app_engagement_push.csv')
ナイーブな評価
上の$LATE$の定義に沿って、平均値を求めてストレートに求めます。
EY_Z1 = df.query("push_assigned==1").in_app_purchase.mean()
EY_Z0 = df.query("push_assigned==0").in_app_purchase.mean()
ET_Z1 = df.query("push_assigned==1").push_delivered.mean()
ET_Z0 = df.query("push_assigned==0").push_delivered.mean()
LATE = (EY_Z1 - EY_Z0) / ((ET_Z1 - ET_Z0))
print(LATE)
linearmodelsによる2段階最小二乗法
ライブラリ linearmodels を使って、操作変数法を実施します。このライブラリが入っていない場合は pip installなどで予め入れておく必要があります。
from linearmodels.iv import IV2SLS
iv = IV2SLS.from_formula("in_app_purchase ~ 1 + [push_delivered ~ push_assigned]", df).fit()
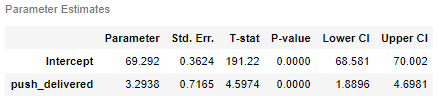
iv.summary.tables[1]
push_delivered、プッシュ通知が届いたかどうかの説明変数の係数は3.29と推定されています。これは、上のナイーブな評価と一致しています。線形モデルの仮定が正しければ、信頼区間も求められます。今回は有意な結果が得られています。
$E[Y|Z=1] - E[Y|Z=0]$ で推定した2.4という値は、やはり過小評価されていました。不服従にきちんと対応しないと、施策の効果を正しく検証できませんね。
参考
[1]Causal Inference Brave and True 09 - Non Compliance and LATE