はじめに
A/Bテストを実施する際にしばしば発生するノンコンプライアンス(不遵守)という問題とその対処法について、具体例とPythonによるシミュレーションを交えながらまとめました。内容に誤り等ございましたらご指摘いただけますと幸いです。
A/Bテスト(RCT)とは
A/Bテストとは異なる複数のパターンを比較する手法の総称です。
例えば、「パターンAとパターンBのWeb広告を配信し、クリック率を比較する」というものです。そして、その結果から「クリック率が低い方のWeb広告の配信をやめ、クリック率が高い方のWeb広告を配信を増やす」という意思決定に繋げます。このようなプロセスを繰り返すことで、意思決定の精度(ここで言う広告のクリック率)を向上させていくことがA/Bテストの目的です。
データ分析を生業とする人たちの中ではもう少し厳密に「2つ(以上)の実験群(コントロール群と介入群)を比較するコントロール実験」というように定義されることも多く、ランダム化比較試験(RCT: Randomized Controlled Trial)と呼ばれることもあります。
A/Bテストのポイント
A/Bテストを用いて複数のパターンを"正しく"比較・評価するためにはいくつかの前提条件が求められることがありますが、特にランダム化が重要な条件の1つとなることが多いです。
他にも必要な前提条件や特殊なランダム化の条件などありますが、本記事では説明を割愛します。
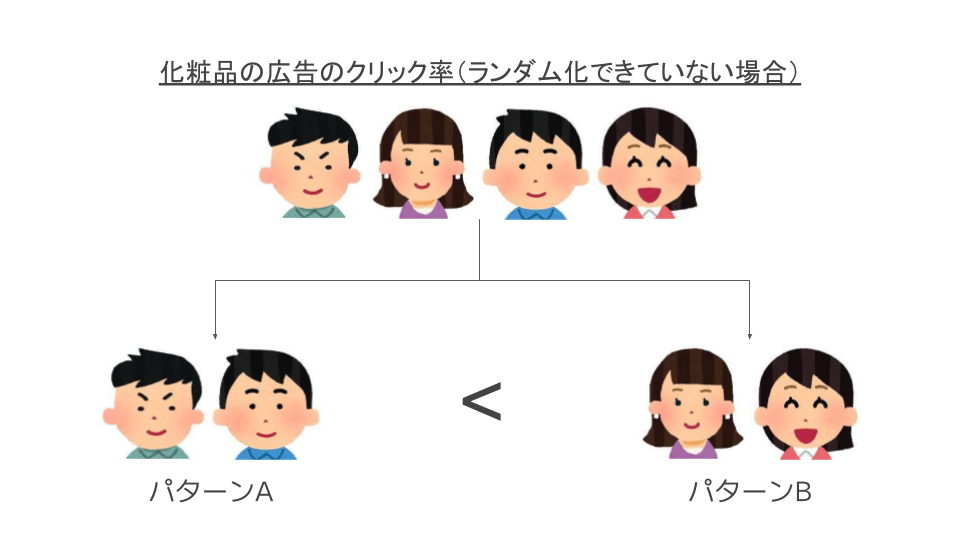
ランダム化が必要となる直感的な理解のために、化粧品の広告をうつ例を考えます。
従来の広告をパターンA、新しい広告をパターンBとすると、パターンBの配信を「処置」と言い、パターンBの広告を配信させることを「処置を割付ける」と表現します。
このとき、ランダム配信ではなく、
- パターンAの広告は男性にだけ配信
- パターンBの広告は女性にだけ配信
としてクリック率を比較したらどうなるでしょうか?おそらく男性よりも女性の方が化粧品への興味関心が強い傾向にあるため、広告の出来によらず、パターンAよりパターンBの方がクリック率が高くなるはずです。
そのため、パターンAとパターンBの広告配信先をランダム化(男女比率が均等になるように)する必要があるのです。
ランダムに広告を配信した結果をもとに、パターンAとパターンBのクリック率を比較・評価します。
A/Bテストの結果を比較・評価する手法としては、統計的仮設検定などが定番です。
ノンコンプライアンス(不遵守)とは
ノンコンプライアンス(不遵守)とは、処置が割付けられたものの、その割付けに従わないことを指します。
例えば、CRMのメールマーケティングが挙げられます。化粧品会社にて新商品の発売を、会員へのメールで宣伝するとします。このとき、ランダムに
- $Z=1$: メールが送信された会員(処置が割付けられたグループ)
- $Z=0$: メールが送信されない会員(処置が割付けられていないグループ)
に分け、「メールが新商品購入に寄与した効果」すなわち「メールを見た会員はメールを見ていない会員と比べてどれほど新商品の購入率が高いか」を考えます。
- $Y=1$: 商品を購入する
- $Y=0$: 商品を購入しない
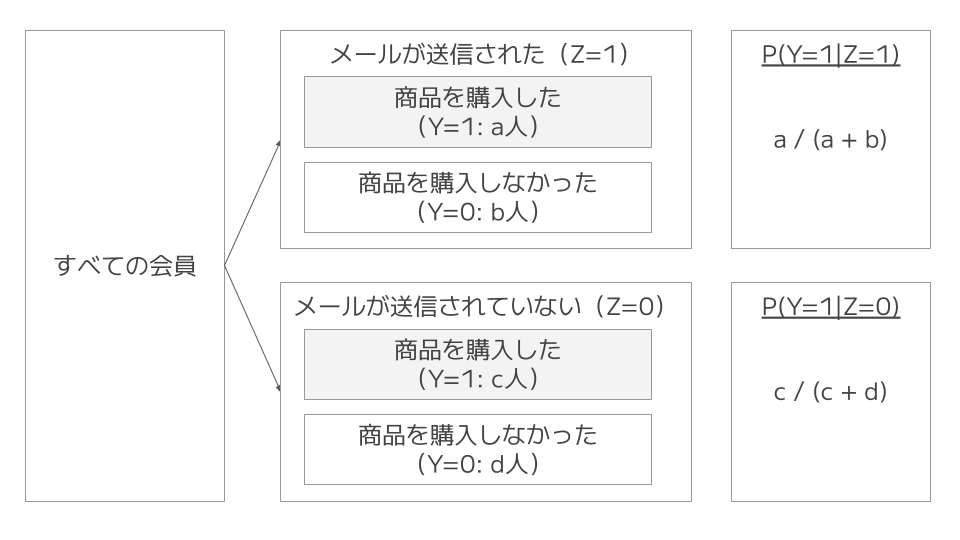
とし、確率を表す記号を$\ P( \cdot ) \ $とすると、一見、
P(Y=1| \ Z=1) - P(Y=1| \ Z=0) \tag{1}
と考えれば良さそうです。$P(Y=1| \ Z=1) \ $と$\ P(Y=1| \ Z=0) \ $は各々、下図の塗りつぶし部分の条件付き確率です。
$P(Y|Z) \ $は$\ Z \ $で条件づけた際の$\ Y \ $の確率(条件付き確率)です。
- $P(Y=1| \ Z=1) \ $は$\ Z=1$(メールが配信された会員)のうち、$\ Y=1$(商品を購入した会員)の割合
- $P(Y=1| \ Z=0) \ $は$\ Z=0$(メールが配信されていない会員)のうち、$\ Y=1$(商品を購入した会員)の割合
を表します。
しかし、これではメールの効果を過小評価してしまうことになります。
なぜなら「メールを送信された会員全員がメールを見たとは限らない(ノンコンプライアンス)」かつ「『メールが送信され、かつ、メールを見た(メールの効果がある)会員』から観測される効果が『メールが送信され、かつ、メールを見た(メールの効果がある)会員』と『メールが送信されたものの見ていない(効果0の)会員』に分散されて算出される」からです。
ここで、実際のメールマーケティングの現場では、「メールを見たor見ていない」は「メールを開封したor開封していない」で判断することができます。
HTMLメールであれば、「メールを開封したor開封していない」は、ツールを利用することで確認することができます。
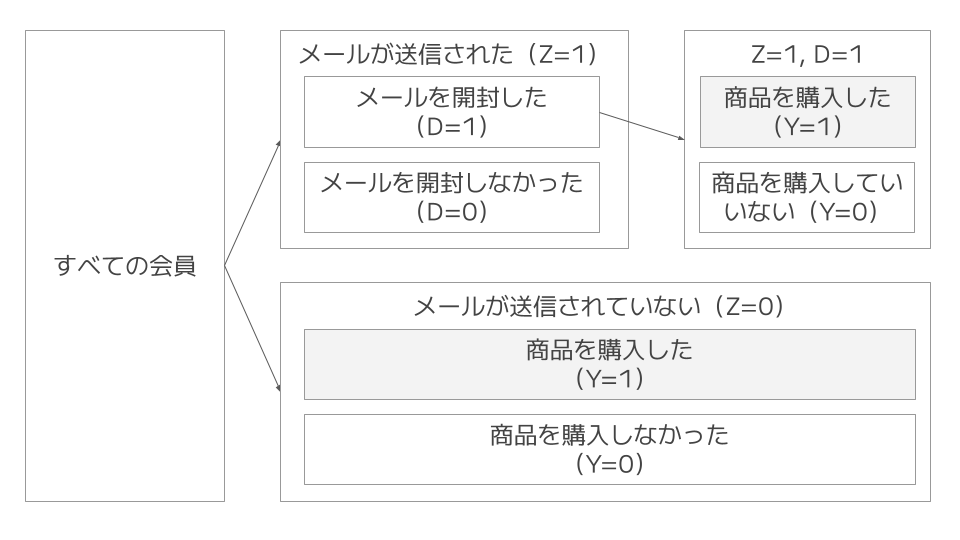
次に、
- $D=1$: メールを見た会員
- $D=0$: メールを見ていない会員
とし、メールを配信された会員に限定して、「メールを見た会員のうち、商品を購入する割合」と「メールを見ていない会員のうち、商品を購入する割合」の差、すなわち、
P(Y=1| \ Z=1, D=1) - P(Y=1| \ Z=1, D=0) \tag{2}
をメールの効果と考えるのはどうでしょう。$P(Y=1| \ Z=1, D=1) \ $と$\ P(Y=1| \ Z=1, D=0) \ $は各々、下図の塗りつぶし部分の条件付き確率です。
これだと、今度はメールの効果を過大評価してしまうことになります。
なぜなら、「メールを見る(開封する)会員は、メールを見ない(開封しない)会員に比べて潜在的に購入意欲が高い」と考えられるからです。逆から考えると、購入意欲が高い人ほどメールが送信されたときにメールを開封する傾向にあるというイメージです。
では次に、「メールが送信され、かつ、メールを見た会員のうち、商品を購入する割合」と「メールが送信されていない会員のうち、商品を購入する割合」の差、すなわち、
P(Y=1| \ Z=1, D=1) - P(Y=1| \ Z=0) \tag{3}
をメールの効果と考えるのはどうでしょう。$P(Y=1| \ Z=1, D=1) \ $と$\ P(Y=1| \ Z=0) \ $は各々、下図の塗りつぶし部分の条件付き確率です。
これも過大評価になってしまいます。理由は先ほどと同様に、「メールを見る(開封する)会員は、メールを見ない(開封しない)会員に比べて潜在的に購入意欲が高い」と考えられるからです。
以上のような理由から、ノンコンプライアンスが生じている場合、メールの平均的な効果(ATE)を計算することはできません。そこで、「メールを見た会員のおける平均的な効果(ATT)」、すなわち「メールを見た会員が、もしメールを見ていなかったら、どれだけ購入率が下がっていたか」を計算します。今回の例では、
\frac{P(Y=1| \ Z=1) - P(Y=1| \ Z=0)}{P(D=1| \ Z=1)} \tag{4}
と計算することができます。(詳細は後述)
さまざまな処置効果については、こちらをご参照ください。
Pythonを用いたシミュレーション
Pythonでデータを自作し、(1)~(4)式を計算してみます。
メールの効果を0.3、すなわち、メールを見ると購入率が30%増加すると設定しています。
# 必要なライブラリのインポート
import numpy as np
import pandas as pd
from scipy.special import expit
# データの設定
np.random.seed(0)
size = 2000
# 購入意欲の高さ
X = np.random.uniform(-5, 1, size=size)
# メール配信の有無
Z = np.array([])
# メールの開封
d_prob = expit(X)
D = np.array([])
for i in range(size):
Z_i = np.random.choice(2, size=1, p=[0.5, 0.5])[0]
Z = np.append(Z, Z_i)
D_i = np.random.choice(2, size=1, p=[1-d_prob[i], d_prob[i]])[0]
D = np.append(D, Z_i*D_i)
# 購入の有無
y_prob = (X+5)/24 + 0.3*D # メールの効果: 0.3
Y = np.array([])
for i in range(size):
Y_i = np.random.choice(2, size=1, p=[1-y_prob[i], y_prob[i]])[0]
Y = np.append(Y, Y_i)
# データフレームに格納
df = pd.DataFrame({'メール配信の有無': Z, 'メールの開封': D, '購入の有無': Y}).astype('int')
df.head()
シミュレーション(1)
まず(1)式、すなわち、
P(Y=1| \ Z=1) - P(Y=1| \ Z=0)
を計算してみます。
# (1)式: P(Y=1| Z=1) - P(Y=1| Z=0)
df_z1 = df[df['メール配信の有無']==1]
df_z0 = df[df['メール配信の有無']==0]
print((df_z1['購入の有無'].sum() / len(df_z1)) - (df_z0['購入の有無'].sum() / len(df_z0)))
(出力結果)
0.06186372591100692
効果は0.3なので、かなり過小評価されているようです。
シミュレーション(2)
次に(2)式、すなわち、
P(Y=1| \ Z=1, D=1) - P(Y=1| \ Z=1, D=0)
を計算してみます。
# (2)式: P(Y=1| Z=1, D=1) - P(Y=1| Z=1, D=0)
df_z1 = df[df['メール配信の有無']==1]
df_z1_d1 = df_z1[df_z1['メールの開封']==1]
df_z1_d0 = df_z1[df_z1['メールの開封']==0]
print((df_z1_d1['購入の有無'].sum() / len(df_z1_d1)) - (df_z1_d0['購入の有無'].sum() / len(df_z1_d0)))
(出力結果)
0.40170605332996334
効果は0.3なので、過大評価されているようです。
シミュレーション(3)
次に(3)式、すなわち、
P(Y=1| \ Z=1, D=1) - P(Y=1| \ Z=0)
を計算してみます。
# (3)式: P(Y=1| Z=1, D=1) - P(Y=1| Z=0)
df_z1 = df[df['メール配信の有無']==1]
df_z0 = df[df['メール配信の有無']==0]
df_z1_d1 = df_z1[df_z1['メールの開封']==1]
print((df_z1_d1['購入の有無'].sum() / len(df_z1_d1)) - (df_z0['購入の有無'].sum() / len(df_z0)))
(出力結果)
0.37928140571728297
効果は0.3なので、過大評価されているようです。
シミュレーション(4)
次に(4)式、すなわち、
\frac{P(Y=1| \ Z=1) - P(Y=1| \ Z=0)}{P(D=1| \ Z=1)}
を計算してみます。
# (4)式: {(P(Y=1| Z=1) - P(Y=1| Z=0)) / (P(D=1| Z=1))}
df_z1 = df[df['メール配信の有無']==1]
df_z0 = df[df['メール配信の有無']==0]
df_z1_d1 = df_z1[df_z1['メールの開封']==1]
print(((df_z1['購入の有無'].sum() / len(df_z1)) - (df_z0['購入の有無'].sum() / len(df_z0)))/ (len(df_z1_d1) / len(df_z1)))
(出力結果)
0.29483346446367686
効果は0.3なので、よく推定できているようです。
理論的な背景
A/Bテスト(RCT)におけるノンコンプライアンスは、操作変数法(IV法: Instrumental Variable method)の最も重要な応用ケースの1つです。先ほどのメールマーケティングの例で使用した、(4)式を導出します。
操作変数とは、メールマーケティングの例では、購入$\ Y_i \ $には影響を与えず、メールの開封$\ D_i \ $に影響を与える変数、すなわち、メールの送信$\ Z_i \ $にあたり、次の条件を満たします。
$$Cov[Z_i, D_i] \neq 0 \ , \ Cov[Z_i, e_i] = 0 \tag{a}$$
操作変数につきましては、こちらの記事もご参照ください。
操作変数法(IV法)
次のようなモデルを考えます。
Y_i = \beta_0 + \beta_1 D_i + e_i \ , \ Cov[D_i, e_i] \neq 0 \tag{b}
ここで、$Cov[D_i, e_i] \ $は$\ D_i \ $と$\ e_i \ $の共分散を表し、メールマーケティングの例では、
- $Y_i: $商品の購入
- $D_i: $メールの開封
にあたります。$Cov[D_i, e_i] \neq 0 \ $は、メールを開封するかどうかを表す変数$\ D_i \ $と、会員の購入意欲が含まれている誤差項$\ e_i \ $に相関があることを示しています。
$Cov[D_i, e_i] \neq 0 \ $の場合、(a)式のOLS推定量$\ \hat{\beta_1} \ $は識別できません。
そのため、(b)式の両辺と$\ Z_i \ $の共分散とって整理すると
Cov[Z_i, Y_i] = \beta_1 Cov[Z_i, D_i] + Cov[Z_i, u_i]
ここで、(a)式より、
\beta_1 = \frac{Cov[Z_i, Y_i]}{Cov[Z_i, D_i]} \tag{c}
と識別することができます。これを操作変数推定量(IV estimator)と言います。
OLS推定量につきましては、こちらの記事もご参照ください。
Wald推定量
上記の操作変数法の中でも、メールマーケティングの例のような「操作変数がダミー変数」の場合、Wald推定量を導出することができます。
$P(Z_i=1)=p $とおくと、繰り返し期待値の法則から
\begin{align}
Cov[Z_i, Y_i] &= E[Z_i \ E[Y_i| \ Z_i]] - E[Z_i]E[E[Y_i| \ Z_i]] \\
&= pE[Y_i| \ Z_i=1] + (1-p)E[Y_i| \ Z_i=0] - (pE[Y_i| \ Z_i=1]) \\
&= (E[Y_i| \ Z_i=1] - E[Y_i| \ Z_i=0])p(1-p)
\end{align}
同様にして
Cov[Z_i, D_i] = (E[D_i| \ Z_i=1] - E[D_i| \ Z_i=0])p(1-p)
これらの結果を(c)式に代入すると
\beta_1 = \frac{Cov[Z_i, Y_i]}{Cov[Z_i, D_i]} = \frac{E[Y_i| \ Z_i=1] - E[Y_i| \ Z_i=0]}{E[D_i| \ Z_i=1] - E[D_i| \ Z_i=0]} \tag{d}
ここで、メールマーケティングの例では
\begin{align}
E[Y_i| \ Z_i=1] &= 1 \cdot P(Y_i=1 | \ Z_i=1) + 0 \cdot P(Y_i=0 | \ Z_i=1) \\
&= P(Y_i=1 | \ Z_i=1) \\ \\
E[Y_i| \ Z_i=0] &= 1 \cdot P(Y_i=1 | \ Z_i=0) + 0 \cdot P(Y_i=0 | \ Z_i=0) \\
&= P(Y_i=1 | \ Z_i=0) \\ \\
E[D_i| \ Z_i=1] &= 1 \cdot P(D_i=1 | \ Z_i=1) + 0 \cdot P(D_i=0 | \ Z_i=1) \\
&= P(D_i=1 | \ Z_i=1) \\ \\
E[D_i| \ Z_i=0] &= 1 \cdot P(D_i=1 | \ Z_i=0) + 0 \cdot P(D_i=0 | \ Z_i=0) \\
&= P(D_i=1 | \ Z_i=0) \\
&= 0
\end{align}
となります。
したがって、これらを(d)式に代入すると、
\beta_1 = \frac{E[Y_i| \ Z_i=1] - E[Y_i| \ Z_i=0]}{E[D_i| \ Z_i=1] - E[D_i| \ Z_i=0]} = \frac{P(Y_i=1| \ Z_i=1) - P(Y_i=1| \ Z_i=0)}{P(D_i=1| \ Z_i=1)}
となり、(4)式が導出することができました。
$\ P(D_i=1 | \ Z_i=0) \ $は「メールを送信されていない($Z_i=0$)会員のうち、メールを見た($D_i=1$)会員」という存在し得ない状況なので、その確率は0になります。
LATE推定量
観測される変数$\ (Y_i, D_i, Z_i) \ $と潜在的な変数$\ (Y_{1i}, Y_{0i}, D_{1i}, D_{0i}) \ $の間に
Y_i = D_i Y_{1i} + (1 - D_i) Y_{0i} \\
D_i = Z_i D_{1i} + (1 - Z_i) D_{0i}
という関係が成り立ち、操作変数$\ Z_i \ $に対して
- $(Y_{1i}, Y_{0i}, D_{1i}, D_{0i}) \ $と$\ Z_i \ $は独立
- $P(D_{1i} \neq D_{0i}) \neq 0$
- すべての$\ i \ $について、$D_{1i} - D_{0i} \geq 0 \ $が成り立つ
と仮定する。このとき、
LATE = \frac{E[Y_i| \ Z_i=1] - E[Y_i| \ Z_i=0]}{E[D_i| \ Z_i=1] - E[D_i| \ Z_i=0]}
とおくと、LATEは局所的平均処置効果(LATE: Local Average Treatment Effect)と呼ばれます。
LATEの式は、Wald推定量(4)式と一致しています。
追記
@nekobo さん(Twitter: https://twitter.com/nekobo_01 )がRで実装してくれました!ぜひ、こちらの記事もご覧ください!(@nekobo さん、ありがとうございます!)
おわりに
最後まで読んでいただきありがとうございました。
zennにて「Python×データ分析」をメインテーマに記事を執筆しているので、ご一読いただけますと幸いです。
また、過去にLTや勉強会で発表した資料が下記リンクにてまとめてありますので、こちらもぜひご一読くださいませ。
参考文献
- Duflo et al.(2019)「政策評価のための因果関係の見つけ方」日本評論社
- Kohavi et al.(2021)「A/Bテスト 実践ガイド」ドワンゴ
- 岩崎(2015)「統計的因果推論」朝倉書店
- 末石(2015)「計量経済学」日本評論社
- 高橋(2022)「統計的因果推論の理論と実装」共立出版
- 西山他(2019)「計量経済学」有斐閣
- 星野(2009)「調査観察データの統計科学」岩波書店