初投稿です.
先日最適化理論の講義のレポートで最急降下法のプログラムをPythonで書いたので,
Haskellでも書いてみました.
HaskellはPythonに比べてまだまだ書き方を理解していないので,
こうすればいいよ!というのがあればご教示ください.
最急降下法
次のような制約なし最適化を考えます.
\min_{\mathbf{x} \in \mathbb{R}^n} \; f( \mathbf{x} )
つまり,やりたいことは,$ f(\mathbf{x}) $の最小値と最小解をもとめることです
($f$は凸関数と仮定しています).
例として,$ f(x, y) = (x-1)^2 + (y-2)^2 $を考えてみます.
この関数は,$ (x, y) = (1, 2) $で,最小値$ 0 $を取ります.
図で書くと,次のようになります.
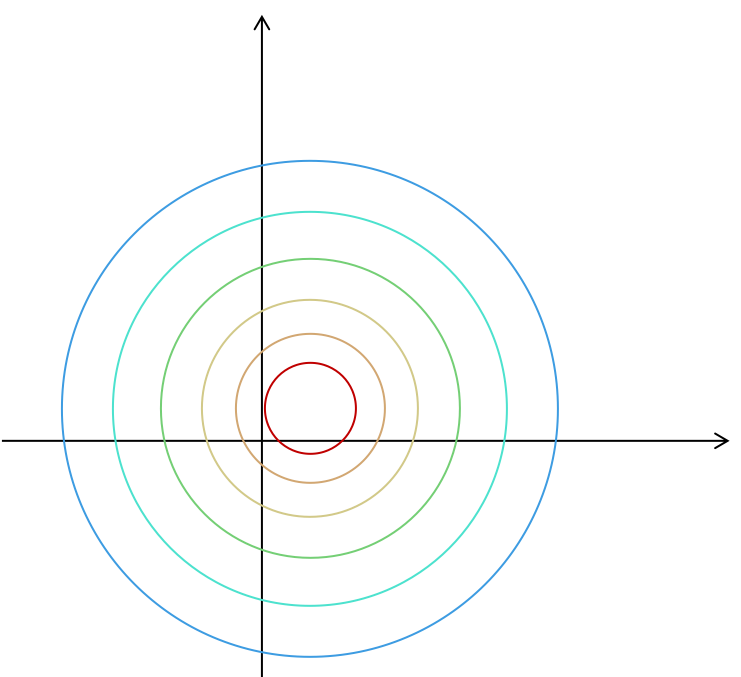
この関数の$(a, b)$における勾配$ \nabla f(a, b) $は,図で書くと次のようになります(緑色).

最急降下法とは,
「$(a, b)$から$ - \nabla f(a, b) $の方にある程度進む」
という戦略をとる最適化の手法です.
この「ある程度」というのは,適当ではありません.
関数値が下がる方向に進みすぎても,進まなすぎてもダメです(下の図を参考程度に).
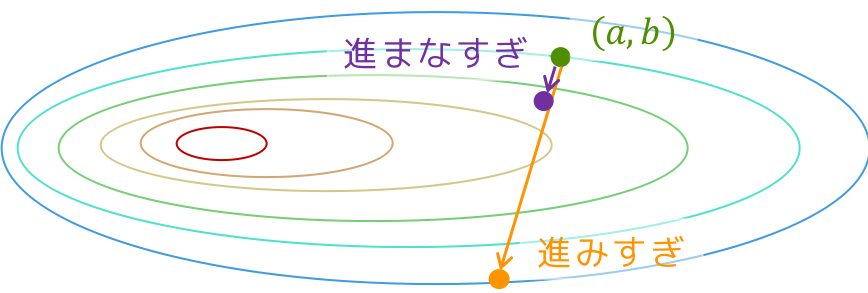
この,「どれくらい進むか」という進み具合を表す幅を「ステップ幅」といい,あとでプログラムを書くときに説明します.
最急降下法の概形を書くと,次のようになります.
- 初期点$x = (x_0, y_0)$, 誤差のパラメータ$eps$を入力として与える.
- $\nabla f(x) < eps$ならば,5へ.
- ステップ幅 $t > 0$を決める.
- $ x \gets x + t (-\nabla f(x)) $として,2へ.
- return $x$
最適解 $ ( x_{\text{opt}}, y_{\text{opt}} ) $ では勾配が $\mathbf{0}$ になるのでそれを終了条件とすればただしく動くはずです.
モジュールのインポート
今回は,Haskellでは標準モジュールのみで解くので,何もインポートしません.
-- 何もいらない(便利なモジュールを知らない)
Pythonでは,numpyのみを使います.
import numpy as np
型宣言
つぎに,ベクトルを表現するのに[Double]などを用いるとわかりにくくなるので,名前を変えます.
type Scalar = Double -- Double型をScalarと呼ぶことにする
type Vector = [Double] -- Double型のリストをVectorと呼ぶことにする
目的関数の定義
今回は,$f(x, y) = (x-1)^2 + (y-2)^2$を最小化することを考えます.
$f(x, y)$の$(x, y)$における微分は次のようになります.
\nabla f(x, y) =
\begin{bmatrix}
2(x-1) \\
2(y-2)
\end{bmatrix}
この$f, \nabla f$をHaskell, Pythonでそれぞれ書きます.
f :: Vector -> Scalar
f (x:y:_) = (x-1.0)^2 + (y-1.0)^2
f' :: Vector -> Vector
f' (x:y:_) = [a, b]
where a = 2*(x - 1.0)
b = 2*(y - 2.0)
def f(x):
return (x[0] - 1.0)**2 + (x[1] - 1.0)**2
def df(x):
a = 2*(x[0] - 1.0)
b = 2*(x[1] - 2.0)
return np.array([a, b])
基本的な関数の定義
僕はHaskellにおけるpythonのnumpyのようなモジュールを知らないので,ベクトルの内積,和,スカラー倍等の計算をする関数を定義します(便利なモジュールがあれば教えてください).
-- ベクトルのスカラー倍
mul :: Scalar -> Vector -> Vector
mul c v = map (* c) v
-- ベクトルの和
add :: Vector -> Vector -> Vector
add xs ys = zipWith (+) xs ys
-- ベクトルの内積
dot :: Vector -> Vector -> Scalar
dot xs ys = foldr (+) 0 $ zipWith (*) xs ys
-- ベクトル v を負にする i.e. (-1) * v を計算する
negative :: Vector -> Vector
negative = map (* (-1))
-- ベクトルの2-ノルムを計算する
norm :: Vector -> Scalar
norm xs = sqrt $ dot xs xs
-- Double型の最大値(maxBoundがなかった?)
doubleMax :: Double
doubleMax = 1e10
pythonでは,numpyがあるのでベクトルの内積,和,スカラー倍等は定義しなくても使えます.
2-ノルムを計算する関数だけ作ります.
def norm(x):
n = np.sum(x**2)
return np.sqrt(n)
main関数の完成像
今回の記事で書くプログラムの完成像は,Haskellだと次のような感じになります.
main :: IO ()
main = do
let x = [5.0, 5.0] -- 初期点
c1 = 0.4 -- パラメータ(後で説明)
c2 = 0.8 -- パラメータ(後で説明)
(v_opt, x_opt) = solve x c1 c2 -- 最適解を求める.
putStr "Optimal Solution : "
print x_opt
putStr "Optimal Value : "
print v_opt
Pythonだと,次のような感じを目標にプログラムを書いていきます.
if __name__ == "__main__":
x0 = np.array([5.0, 5.0]) # 初期点
c1 = 0.4 # パラメータ(後で説明)
c2 = 0.8 # パラメータ(後で説明)
eps = 1e-9 # 終了条件用のパラメータ
sd = SteepestDescent(x0=x0, c1=c1, c2=c2, eps=eps)
sd.solve()
print("Optimal Solution : {}".format(sd.opt))
print("Optimal Value : {}".format(f(sd.opt)))
じゃあ,後は最適解を計算する関数(Pythonだとメソッド)solveを作れば終わりです.
その前にPythonでは
クラスを使ってプログラムを書いていきます.
SteepestDescentクラスのコンストラクタを次のように作ります.
class SteepestDescent(object):
"""
STEEPEST DESCENT METHOD
"""
def __init__(self, x0, c1=0.4, c2=0.8, eps=1e-6):
"""
PARAMETERS:
x : 時刻tに選んだ点
opt : 最適解を格納する変数
c1 : パラメータ(armijoの条件)
c2 : パラメータ(wolfの条件)
eps : 誤差パラメータ
"""
self.x = x0
self.opt = None
self.c1 = c1
self.c2 = c2
self.eps = eps
終了条件
終了条件は,$\nabla f(x, y) < eps$なので,Haskellでは次のように書きます.
eps :: Double
eps = 1e-9
isFiniteState :: Vector -> Bool
isFiniteState v =
let n = (norm . f') v
in if n < eps then True else False
Pythonでは,次のように書きます.
def isFinite(self):
g = df(self.x)
n = norm(g)
if n < self.eps:
return True
else:
return False
次に,solve関数(メソッド)の概形を書きます.
solve :: Vector -> Scalar -> Scalar -> (Scalar, Vector)
solve x c1 c2
| isFiniteState x = (f x, x) -- 終了条件を満たしたら終了
| otherwise = -- 満たしていなかったら,
let d = negative (f' x) -- -f'(x) を計算して,
t = getStepSize x 1 c1 c2 0 doubleMax -- ステップ幅を求めて,
y = add x (mul t d) -- x = x - t f'(x)として
in solve y c1 c2 -- 解き直す
Pythonだと,こう書きました.
def solve(self):
while not self.isFinite(): # 終了条件を満たしていない間
d = -df(self.x) # - f'(x)を計算して,
t = self.getStepSize() # ステップ幅を求めて,
self.x = self.x + t * d # x = x - t f'(x)として解き直す
self.opt = self.x
Haskell, Pythonのどちらにおいても,あとはステップ幅を求めるだけです.
ステップ幅をもとめる
最初の方で言ったように,ステップ幅は大きすぎても小さすぎてもいけません(再掲).
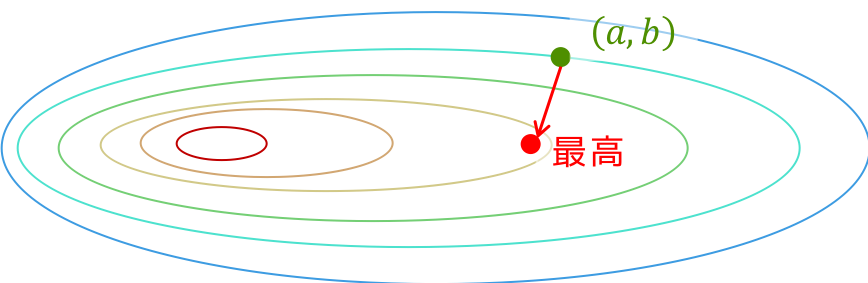
理想としては,$ \mathbf{d} = - \nabla f(\mathbf{x}) $としたときに
\min_t f( \mathbf{x} + t \mathbf{d})
を満たすtが最も良いステップ幅です.これをexact line searchと言うそうです.
しかし,exact line searchをしようとすると別の最適化問題を解かなければならないので,
今回はinexact line searchでステップ幅を求めようと思います.
inexact line search とは,大きすぎず小さすぎないステップ幅$ t > 0 $をもとめる方法です.
つまり,次のようなプログラムを書きたいわけです.
- ステップ幅$t>0$を渡す
- if $t$が大きすぎる$ \to $ $t$を小さくして,1へ
- else if $t$が小さすぎる$ \to $ $t$を大きくして,1へ
- else return t
ステップ幅が大きすぎないか,という問題はArmijoの条件というものを使って判定できます.
Armijoの条件:
$ \phi(t) = f( \mathbf{x} + t \mathbf{d})$としたときに,$c_1 \in (0, 1)$に対して
\phi (t) \leq \phi(0) + c_1 t \phi'(0)
を満たす$t > 0$を選ぶ.
また,ステップ幅が小さすぎないか,という問題は,Wolfの条件というものを使って判定できます.
Wolfの条件:
$0 < c_1 < c_2 < 1$に対して,
\phi (t) \leq \phi(0) + c_1 t \phi'(0)\\
\phi' (t) \geq c_2 \phi' (0)
を満たす$t > 0$を選ぶ.
(Wolfの条件の1つ目は,Armijoの条件のことです)
この辺は数学書に書いてあると思うので,なんでこれを満たせば良いか,等が気になる人は調べてみてください.
どういう式を満たせばステップ幅が適当か,という式がわかったので,あとはプログラムを書くだけです.
追記:コメントアウトしてあるところは僕が書いたコードで,
コメントアウトされていないところは,@kmrt7010さんにおしえていただいたコードです!
ありがとうございます!
-- コメントアウトされているところは
-- 僕が書いた綺麗ではないコードです
{-
armijo :: Vector -> Scalar -> Scalar -> Bool
armijo v t c =
let z = f v
d = negative (f' v)
dx = add v (mul t d)
y = f dx
p0 = dot (f' v) d
in if y <= z + t*c*p0 then True
else False
-}
armijo :: Vector -> Scalar -> Scalar -> Bool
armijo v t c = y <= z + t*c*p0
where z = f v
d = negative (f' v)
dx = add v (mul t d)
y = f dx
p0 = dot (f' v) d
{-
wolf :: Vector -> Scalar -> Scalar -> Bool
wolf v t c =
let d = negative (f' v)
dx = add v (mul t d)
p0 = dot (f' v) d
pt = dot (f' dx) d
in if pt >= c*p0 then True
else False
-}
wolf :: Vector -> Scalar -> Scalar -> Bool
wolf v t c = pt >= c*p0
where d = negative(f' v)
dx = add v (mul t d)
p0 = dot (f' v) d
pt = dot (f' dx) d
{-
getStepSize :: Vector -> Scalar -> Scalar -> Scalar -> Scalar -> Scalar -> Scalar
getStepSize x t c1 c2 a b
| not (armijo x t c1) = if t < doubleMax then getStepSize x ((a + t)/2.0) c1 c2 a t
else getStepSize x (2*a) c1 c2 a t
| not (wolf x t c2) = if b < doubleMax then getStepSize x ((t + b)/2.0) c1 c2 t b
else getStepSize x (2*t) c1 c2 t b
| otherwise = t
-}
getStepSize :: Vector -> Scalar -> Scalar -> Scalar -> Scalar -> Scalar -> Scalar
getStepSize x c1 c2 a t b
| not (armijo x t c1) && t < doubleMax = getStepSize x c1 c2 a ((a+t)/2) t
| not (armijo x t c1) = getStepSize x c1 c2 a (2*a) t
| not (wolf x t c2) && t < doubleMax = getStepSize x c1 c2 t ((t+b)/2) b
| not (wolf x t c2) = getStepSize x c1 c2 t (2*t) b
| otherwise = t
この辺の書き方が少し汚い気がするので,良い書き方があれば教えて欲しいです.
一方,Pythonでは次のようにかけます.
def armijo(self, t, c):
z = f(self.x)
d = -df(self.x)
dx = self.x + t*d
y = f(dx) # left hand side of armijo's condition
p0 = np.dot(df(self.x), d) # armijo's cond. phi'(t)
if y <= z + t*c*p0:
return True
else:
return False
def wolf(self, t, c):
d = -df(self.x)
dx = self.x + t*d
p0 = np.dot(df(self.x), d) # phi'(0)
pt = np.dot(df(dx), d) # phi'(t)
if pt >= c*p0:
return True
else:
return False
def getStepSize(self):
# initialize parameters
alpha = 0
beta = sys.maxsize
t = 1
c1 = self.c1
c2 = self.c2
while True:
if not self.armijo(t, c1):
beta = t
elif not self.wolf(t, c2):
alpha = t
else:
break
if beta < sys.maxsize:
t = (alpha + beta) / 2.0
else:
t = 2*alpha
return t
はい,これで欲しい関数などは全部求められました.
あとは実行するだけです.
実行結果
$f(x, y) = (x-1)^2 +(y-2)^2$に対して実行してみました.
Haskellでの実行結果のみ載せてます.
Optimal Solution : [1.0, 2.0]
Optimal Value : 0.0
正しく計算できてますね!
まとめとか
ほんとはNewton法を書きたかったけど,Haskellで固有値を求める関数がどれかわからなかったので断念しました(Pythonだとnp.linalg.eigvals(A)で行列Aの固有値を求められた).
こういうのがあるよ!っていうのを知ってる方がいらっしゃいましたら,是非教えてください.
この前@lotzさんにNumeric.LinearAlgebraに固有値計算の関数があることを教えていただきました.調べてみると,コレスキー分解もできるみたいなので,Newton法も書けそうです!
近いうちに,研究や心に余裕ができたら書かせていただきます.