強化学習が大好きなので記事を書いてみることにしました。お手やわやわにお願いします。
目次
0.はじめに
1.強化学習の問題設定
2.マルコフ決定過程
3.ベルマン方程式
4.おわりに
0.はじめに
こんにちは、強化学習大好きマンのかんといいます。
強化学習を勉強する上で一番辛いのは、数学的なややこしさだと個人的に思っていて特に序盤で詰まって諦めることが多いのかなと思います。実際自分がそうで、序盤の意味がわからなさすぎて半年くらい放置してました。
強化学習は数学がとても難しいと言われていて、自分も式の意味レベルくらいの理解で厳密な数学的理解はできていないところもあります。それでも__強化学習は本当に面白い分野だと思っている__ので布教したくて記事を書こうと思いました。
できるだけ具体例をまじえて__勉強中の人はもちろん強化学習について何も知らないという人でもわかるよう書く__つもりです。
間違いやもっとわかりやすい書き方などがありましたら指摘していただけるととても助かります。よろしくお願いします。
強化学習の最初の最初なのでこの記事は長くなると思いますが最後まで読んでいただけると嬉しいです。
では、具体的なゲームを通して強化学習の問題設定から解説してみたいと思います。
1.強化学習の問題設定
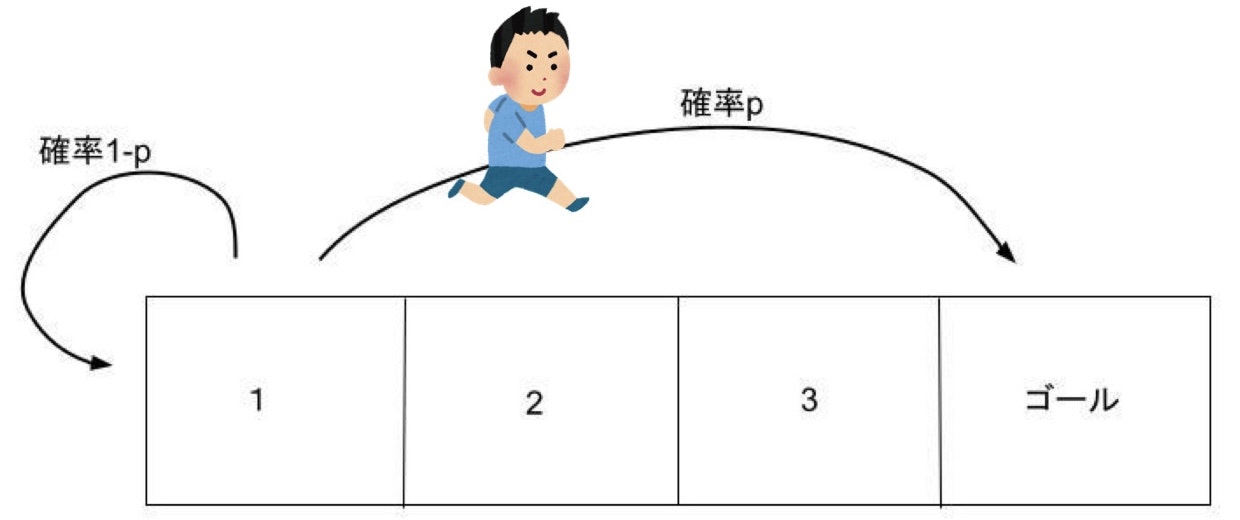
あなたは今から友達とこの迷路(と呼べるのか?)を使ってゲームをしようとしています。この迷路にはルールがあって
- 2,3のマスでは1回の行動で右か左に1マス動ける。1のマスから左に動くと確率pでいきなりゴールへ行けて、確率1-pで1に戻る。(普通に右に行くこともできる)
- 別のマスに移動したとき-1ポイントされるが、ゴールに到達したときは-1ポイントではなく10ポイントもらえる。1で左に行き1に戻ってきた場合も-1ポイント。
- 最初スタートする場所を1,2のどちらかから選べる。
- ゴールするまでに得たポイントの合計が高い人が勝ち
というものです。
さて、1,2のどちらのマスからスタートするのが勝てそうでしょうか。pが大きいほど1からスタートした方がよいことはわかりますが具体的にpが何以上なら1からスタートするべきでしょうか。
2から右に行き続けたとき-1+10=9の9ポイントでゲームを終了するので、期待値が9より大きい時は1からスタートして左に行った方が良さそうです。1に戻ってきてしまい-1ポイントされても途中で諦めず必ず左に行く選択をする場合、1回目で行けるとき確率はpでポイントは10、2回目で行ける時確率は(1-p)pでポイントは-1+10、3回目で行ける時確率は(1-p)(1-p)pでポイントは-1-1+10、4回目で行ける時は、、、と考えると期待値Eは
$$E = p \times10+(1-p)p\times(-1+10)+(1-p)(1-p)p\times(-1-1+10)+・・・$$
$$=p\sum_{n=0}^{\infty}(1-p)^n(-n+10)=10p\sum_{n=0}^{\infty}(1-p)^n+p(1-p)\frac{d}{dp}\sum_{n=0}^{\infty}(1-p)^n $$
$$=10-\frac{1}{p}+1=11-\frac{1}{p} $$
となって11-1/p>9を計算するとpが1/2より大きい時は1からスタートした方がよいことがわかります。
(計算をかなりはしょりましたごめんなさい、(-n+10)を分配法則で分けて10の方は普通に計算、-nの方はpで(1-p)^nを微分すれば-nが下に降りてくることを利用しました)
面白みのないゲームを例に取りましたが、このように
1.ある__状態__から(ここではマス)
2.__行動__を__選択__し(ここでいう右に行くか左に行くかを決定し)
3.__次の状態__への__確率的な遷移__をして(ここでいう1マスの1-p,pのこと、普通のマスでは確率1で行きたい方向に移動すると解釈できる。同じマスにいても行動によって行く可能性のあるマスや、確率が違うことに注意。例えば1で左という行動を選択すれば1-pで1,pでゴールだが右を選択すれば確率1で2に移動)
4.__報酬__を得る(ここでいうポイントのこと)
というような1,2,3,4の過程を繰り返して得られる__報酬の和を最大にするような行動の仕方__(このマスにいる時はこう行動する方がいいといったような)を求めよう!というのが__強化学習の目的__です。
2.マルコフ決定過程
強化学習の根幹ともいえる__マルコフ決定過程(Markov decision process 略してMDP)__の話です。大まかには上の1,2,3,4の過程のことですが用語をまじえながら改めて説明をしてみます。
まずはよく出てくる用語の説明
- エージェント:強化学習において実際にある状態で意思決定を行い、上のような1,2,3,4の過程を経験する存在のこと
- 状態:英語でstateなので__s__とよくかかれる。上のゲームでいうマスのこと
- 行動:英語でactionなので__a__とよくかかれる。上のゲームでいう右に行く、左に行く
- 方策:よく__π__と書かれる。エージェントが__ある状態sで行動aを選ぶ確率__のこと。この書き方からわかる通り条件付き確率なのでπ(a|s)とも書かれる。本や記事によっては政策と書かれているものもある。
- (状態)遷移確率:エージェントが__ある状態sで行動aを選んだとき次の状態s'にいく確率__のこと。この書き方からわかる通り条件付き確率なのでp(s'|s,a)とも書かれる
- 報酬:英語でrewardなのでよく__r__と書かれる。エージェントがある状態に遷移した時に得るポイントのこと。状態s,s'、行動aで決まるものなのでr(s,a,s')と書かれることもある。
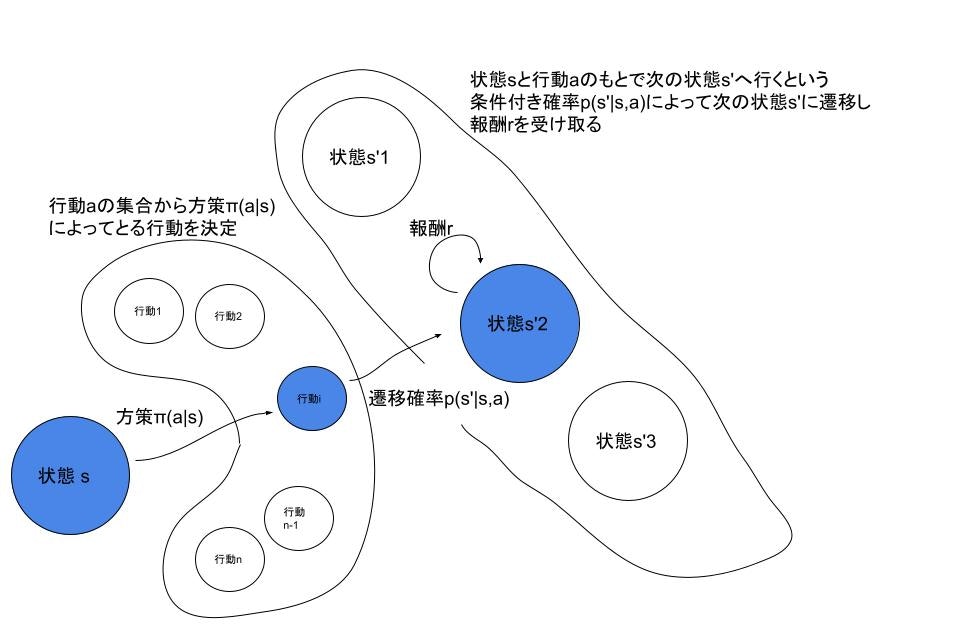
※図では状態s'が3個しかないが何個でもOK
図のようにしてエージェントが__状態sから方策π(a|s)にしたがって行動aを決定__し、__状態遷移確率p(s'|s,a)にしたがって次の状態s'にいって__報酬rを得る。そしてまた方策にしたがって、、を繰り返す過程を__マルコフ決定過程__といいます。
注意しなければならないのは行動を決定する際、考慮するのは今いる状態sのみで__今まで経験してきた状態やしてきた行動は考慮しない__ということです。このような性質を__マルコフ性__といいます。(方策がπ(a|s)と書かれている通り今いる状態sしか考慮していません。)
エージェントが報酬をr1,r2,r3、、と得る時r1+r2+r3+...を__最大にする方策πを探すのが強化学習の目的__ということになります。
3.状態価値関数
さて、強化学習らしくなってきました。
強化学習では現在エージェントがいる状態をs、遷移した次の状態をs'とよく書きますが、
エージェントが状態を次々に移動していくのを意識して__時刻tにおける状態を$s_t$__と書きます。
_s'は$s{t+1}$__ということになりますね。
この添字tを使えばマルコフ決定過程は時刻tの状態$s_t$において、方策πにしたがって行動$a_t$を決定し、遷移確率$p(s_{t+1}|s_t,a_t)$にしたがって状態$s_{t+1}$に遷移し、報酬$r_{t+1}$を受け取るのを繰り返す過程のことです。
強化学習の目的はすべてのtに対して時刻tからの報酬の和 $\sum_{n=1}^{\infty}r_{t+n}$を最大にする方策を見つけることになります。(大事なので何回も言わせてください)
ここでエージェントの気持ちになって考えると__遠い未来(上のシグマでいうnが大きい時)の報酬は直近の報酬より魅力が少ない__気がしませんか?
ぼくはすぐ目先の利益ばかり考えて行動してしまいます。
ということで時刻tから見て__nステップ先に得られる報酬は$\gamma^{n-1}$をかけて割り引く__ことにします。
つまり次の状態での報酬は割り引かず、2個先の報酬は$\gamma$をかけて割り引く、3個先の報酬は$\gamma^2$をかけて割り引く、4個先の報酬は、、といった感じです。
こうすると時刻tにおける最大にしたい報酬の和は$\sum_{n=1}^{\infty}\gamma^{n-1}r_{t+n}$とかけます。
(が0<$\gamma$<1の時は目先のこと重視、1<$\gamma$の時は将来を重視、となりますね。)
この$\sum_{n=1}^{\infty}\gamma^{n-1}r_{t+n}$は__割引報酬和__といってよく__$G_t$__とかかれます。
時刻tからの割引報酬の和でこれを最大化する方策を見つけるのが強化学習の(略)
さてこの$G_t$ですが、次の状態$s_{t+1}$での割引報酬和$G_{t+1}$を考えると
$$G_t=r_{t+1}+\gamma G_{t+1}$$
と書けることがわかります。
時刻tにおいての__状態$s_t$から得られる割引報酬和$G_t$は次の__状態$s{t+1}$に遷移した時に得られる報酬$r{t+1}$と$\gamma$で割引された状態$s_{t+1}$から得られる割引報酬和$G_{t+1}$__を足したものであるということです。
もっと噛み砕いて言うと__時刻t以降で得られる報酬=時刻t+1で得られる報酬+時刻t+1以降で得られる報酬__ということになります。
ところが一番上のようなゲームを考えると確率的な遷移があるので、__同じ方策で行動しても割引報酬和$G_t$は試行をするたびに変動する__ことが予想されます。
これではどうやっていい方策を求めればよいかわからないので時刻tにおける__状態$s_t$がある状態$s$で、ある__方策$\pi$にしたがって行動__するときの$G_t$の(条件付き)期待値$E_\pi[G_t|s_t=s]$を最大__にするような方策を見つけることにします。
つまり1回程度の試行では負けるかもしれないけど何回も行えば最終的な報酬の和が最大になるような方策を見つけようということになります。これが強化学(略)
はい、ということで$E_\pi[G_t|s_t=s]$を最大化しようということですね。
ところでエージェントの気持ちになると時刻tにおいて2つの状態$S_1$と$S_2$があった時に、
そこから得られると予想される報酬、$E\pi[G_t|s_t=S_1]$と$E\pi[G_t|s_t=S_2]$を比べた時にその値が大きい状態の方が価値が高い__と思いませんか?
例えば、2つの状態$S_1$と$S_2$は1番上のゲームの1,2マスと思ってください。
上のゲームでは実際に期待値を計算しました。
あの値はまさにマス1にいる時は確率1で左に行くという方策、書くとすれば方策が「$\pi_{絶対左}$」のもとでの$E_{\pi_{絶対左}}[G_t|s_t=マス1]$の値です。
計算の結果からpが1/2より大きい時マス1から始めた方がよいとなりました。
つまりpが1/2より大きい時はマス2よりマス1の方が価値が大きいといえないか、ということです。
強化学習では__$E_\pi[G_t|s_t=s]$は状態$s$の価値__であるとして__状態価値(関数)という名前がついており$\upsilon_\pi(s)$と書きます。__
つまり、__任意の時刻tで状態$s$から方策$\pi$にしたがって行動したとき得られる割引報酬和の期待値__ということで、その値こそが状態sの価値__だということです。
$$\upsilon\pi(s)=E\pi[G_t|s_t=s]$$
注意したいのは__方策$\pi$の関数でもある__ということです。
(p>1/2でマス1からスタートしてもずっと右に行き続けるという方策では割引報酬和は下がりますよね)
この$\upsilon_\pi(s)$をすべての$s$について最大にする方策$\pi$を見つけ(略)
(用語を解説するにつれて「強化学習の目的」がだんだん難しくなっている気がしますごめんなさい)
4.ベルマン方程式
ここが鬼門です。以前自分はここで意味がわからなくなって半年放置してました
どうしても難しくなってしまいそうですが、できるだけ噛み砕いて解説するのでついて来てください!
では上の$G_t=r_{t+1}+\gamma G_{t+1}$の式の両辺の期待値をとって__状態価値関数に関する式__を作ってみましょう。
ただしこの式は__時刻tにおいての状態$s_t$がある$s$で同じであるという前提__
(右辺で$s_t=s$でない、つまり時刻tにおける状態$s_t$が左辺と違うなんてことはないはずです)
なので__条件付き期待値__をとって(方策$\pi$にしたがって行動することも忘れずに)
$$E_\pi[G_t|s_t=s]=E_\pi[r_{t+1}+\gamma G_{t+1}|s_t=s]$$
状態価値関数の定義 $\upsilon_\pi(s)=E_\pi[G_t|s_t=s]$と期待値の線型性から
$$\upsilon_\pi(s)=E_\pi[r_{t+1}|s_t=s]+\gamma E_\pi[G_{t+1}|s_t=s]$$
まず$E_\pi[r_{t+1}|s_t=s]$の項からみていきましょう。
この式の意味は__時刻tにおける状態$s_t$がある状態$s$であるとき、次の状態に遷移してもらえる報酬rの期待値__ですよね。
方策$\pi$と遷移確率で確率がかなり絡んでいるのでややこしそうです。
とる行動a、次の状態s'、そのときもらえる報酬r(s,a,s')を固定して考えてみましょう。
r(s,a,s')がもらえるのはエージェントが確率$\pi(a|s)$で行動aを選び遷移確率$p(s'|s,a)$でs'に遷移するときなので__確率$\pi(a|s)\times p(s'|s,a)$でこの報酬r(s,a,s')をもらえます。__
これはどのa,s',r(s,a,s')でも言えるので__期待値は$\pi(a|s)\times p(s'|s,a)\times r(s,a,s')$をすべてのa,s'で足し合わせればよい__ことになります。
つまり
$$E_\pi[r_{t+1}|s_t=s]=\sum_{a} \Bigl(\sum_{s'}\bigl(\pi(a|s)p(s'|s,a)r(s,a,s')\bigr)\Bigr)$$
$$=\sum_{a} \Bigl(\pi(a|s)\sum_{s'}\bigl(p(s'|s,a)r(s,a,s')\bigr)\Bigr)$$
($\sum_{n}$はすべてのnで足し合わせるという意味です。$\sum_{a},\sum_{s'}$はすべての$a,s'$で和を取るという意味です。)
$\pi(a|s)$はs'の変数ではないのでs'でのシグマから出して上のような式になります。
続いて$E_\pi[G_{t+1}|s_t=s]$ですが、この式の意味は__時刻tにおける状態$s_t$がある状態$s$のとき、時刻t+1以降で得られる割引報酬和の期待値__ですよね。
_t+1以降で得られる割引報酬和の期待値は、次の状態を$s'$とすると状態価値関数の定義から$\upsilon\pi(s')$_とかけますね。
状態$s'$に行き着く確率は上と同じように$\pi(a|s)\times p(s'|s,a)$なので求める期待値は$\pi(a|s)\times p(s'|s,a)\times \upsilon\pi(s')$をすべての$a,s'$で足し合わせたものになります。
式にすると
$$E_\pi[G_{t+1}|s_t=s]=\sum_{a} \Bigl(\sum_{s'}\bigl(\pi(a|s)p(s'|s,a)\upsilon_\pi(s')\bigr)\Bigr)$$
$$=\sum_{a} \Bigl(\pi(a|s)\sum_{s'}\bigl(p(s'|s,a)\upsilon_\pi(s')\bigr)\Bigr)$$
考え方は上の$r(s,a,s')$の時と同じですね。
基本的な式の意味は$G_t=r_{t+1}+\gamma G_{t+1}$と変わってなくて__時刻t以降で得られる報酬=時刻t+1で得られる報酬+時刻t+1以降で得られる報酬__だけど、期待値なので確率で重みづけして和を取っているというだけです。
以上から $\upsilon_\pi(s)=E_\pi[r_{t+1}|s_t=s]+\gamma E_\pi[G_{t+1}|s_t=s]$ は
$$\upsilon_\pi(s)= \sum_{a} \Bigl(\pi(a|s)\sum_{s'}\bigl(p(s'|s,a)r(s,a,s')\bigr)\Bigr)+\gamma \Bigl(\sum_{a}\pi(a|s)\sum_{s'}\bigl(p(s'|s,a)\upsilon_\pi(s')\bigr)\Bigr)$$
$$=\sum_{a} \Bigl(\pi(a|s)\sum_{s'}\bigl(p(s'|s,a)r(s,a,s')+\gamma p(s'|s,a)\upsilon_\pi(s')\bigr)\Bigr)$$
$$=\sum_{a} \Bigl(\pi(a|s)\sum_{s'}p(s'|s,a)\bigl(r(s,a,s')+\gamma \upsilon_\pi(s')\bigr)\Bigr)$$
と変形できます。
本によってはかっこがなかったり、$\pi$が$\sum_{s'}$の中に入っていたりしますが意味は同じですね。
改めて見てみると$\sum$内の $r(s,a,s')+\gamma \upsilon_\pi(s')$ が $G_t=r_{t+1}+\gamma G_{t+1}$の右辺に対応して、上述のこの説明の意味がわかりやすくなったかなと思います。
基本的な式の意味は$G_t=r_{t+1}+\gamma G_{t+1}$と変わってなくて時刻t以降で得られる報酬=時刻t+1で得られる報酬+時刻t+1以降で得られる報酬だけど、期待値なので確率で重みづけして和を取っているというだけ
今導いたこの式が__ベルマン方程式__と呼ばれているもので、強化学習の基本的な方程式です。
$$\upsilon_\pi(s)=\sum_{a} \Bigl(\pi(a|s)\sum_{s'}p(s'|s,a)\bigl(r(s,a,s')+\gamma \upsilon_\pi(s')\bigr)\Bigr)$$
これからこの式を使って上のゲームでどういう方策をとればマスの状態価値を最大にできるのか、その方策をどうやって求めるのかという話になっていきます。
楽しくなってきましたね、このゲームではもう最強になれるかもしれません。
やろうとはならないけど
4.おわりに
お疲れ様でした。
結構重めの内容だったとは思いますが、ここまで読んでいただいてありがとうございます。
次回も重めな内容にはなりそうですが、できるだけわかりやすく強化学習の面白さを伝えたいと思っていますので読んでもらえると嬉しいです。
わかりにくい所や間違っている所があれば指摘していただけるととても助かります、よろしくおねがいします。