この記事は【強化学習】【基本編】2.方策反復法と価値反復法の続きです。
分かりやすさを重視したかったので文がくどくなりましたがお手やわやわにお願いします。
目次
1.モデルフリーな場合の強化学習
2.モンテカルロ法
3.TD法
4.おわりに
1.モデルフリーな場合の強化学習
前回の記事ではある状態$s$ある行動$a$を選んだ時に次の状態$s'$への遷移確率$p(s'|s,a)$が完全にわかっている場合に最適な行動を求める方法を解説しました。
このように遷移確率$p(s'|s,a)$が完全にわかっている場合の手法を__モデルベース__な手法といいます。
しかし現実的な問題に強化学習を適用する際この遷移確率$p(s'|s,a)$は既知でない場合が多いです。このような場合に適用する方法を__モデルフリー__な手法といって、エージェントに環境を実際に探索させて価値関数を求めようというものになります。
具体的には__遷移確率$p(s'|s,a)$が既知でない場合にある方策$\pi(a|s)$での状態価値関数$\upsilon_\pi(s)$を推定する方法__ということですね。
この推定の方法には大きく分けて2つあり__モンテカルロ法__と__TD法__があります。
まずはモンテカルロ法から解説していきます。
2.モンテカルロ法
今回も今まで使ってきた下のようなゲームの設定を使います。
- 2,3のマスでは1回の行動で右か左に1マス動ける。1のマスから左に動くと確率pでいきなりゴールへ行けて、確率1-pで1に戻る。(普通に右に行くこともできる)
- 別のマスに移動したとき-1ポイントされるが、ゴールに到達したときは-1ポイントではなく10ポイントもらえる。1で左に行き1に戻ってきた場合も-1ポイント。
- 最初スタートする場所を1,2のどちらかから選べる。
- ゴールするまでに得たポイントの合計が高い人が勝ち
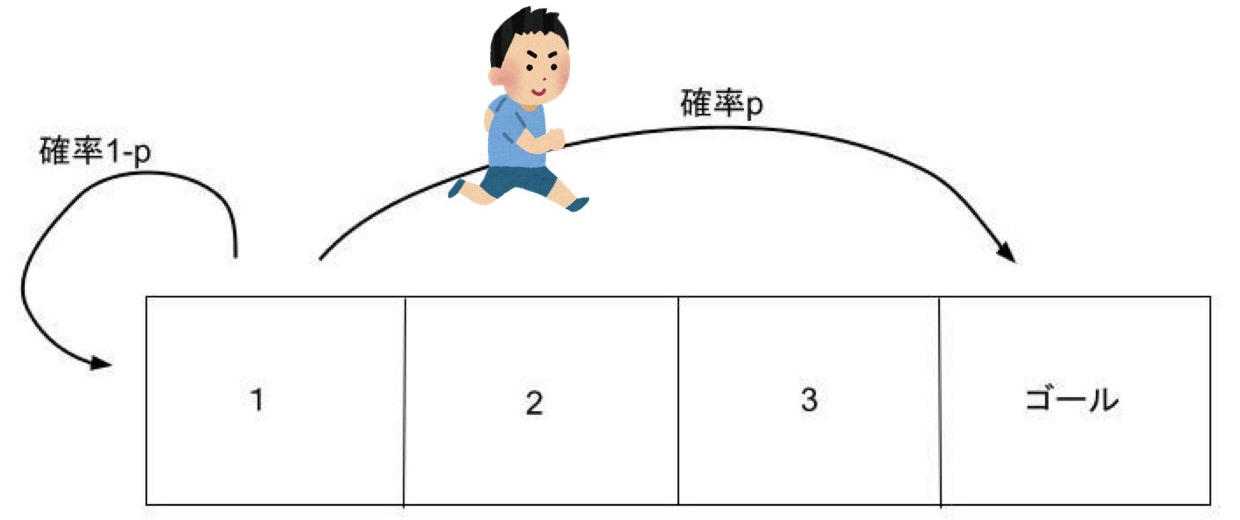
しかし注意してほしいのは__今回は確率pは既知ではないし、マス2で右を選ぶと必ず(確率1で)右に行けることも知らないという前提です。__
イメージしてもらいやすいようこのゲームを例にして説明するというだけなのでよろしくお願いしますね!
ではモンテカルロ法の説明に入りましょう。
状態価値関数$\upsilon_\pi(s)$の定義は覚えていますか?以下のような式でした。
$$\upsilon_\pi(s)=E_\pi[G_t|s_t=s]$$
_状態価値関数$\upsilon\pi(s)$とはその状態sから方策$\pi$にしたがって行動したときに得られる累積報酬和$G(t)$の期待値__であるというものですね。
「期待値」なので$\upsilon_\pi(マス1)$を求めたければマス1からエージェントを何回も行動させてゴールに至るまでに得た累積報酬和の平均を求めればその数値は$\upsilon_\pi(マス1)$になることがわかりますね。
くどくなりますがかなり具体的に考えてみましょう、簡単のため割引率$\gamma$は1とします。この解説の仕方しか思いつきませんでしたすいません
エージェントが__絶対左に行くという方策__を持っているとします。
エージェントをマス1からスタートさせるとエージェントは
マス1→マス1→ゴール
というルートを行きました。このとき$\upsilon_\pi(マス1)$の推定値は何になるでしょうか?
エージェントはマス1を2回経験したのでマス1からの累積報酬和を2個計算できますね。
1つ目(スタート時)は-1+10=9で、2つ目(マス1に戻ってきてから)は10です。よって今の推定値は(9+10)/2の9.5になります。
T回状態sを経験した後での$\upsilon_\pi(s)$の推定値を$V^\pi_{t=T}(s)$とおきます、つまり$V^\pi_{t=2}(マス1)=9.5$です。
$V^\pi_{t=0}(マス2)$はマス2をまだ経験していないので0とおいておきましょう。
では2回目の探索でマス2からスタートさせるとしましょう。するとエージェントは
マス2→マス1→マス1→マス1→ゴール
というルートを行きました。このとき$\upsilon_\pi(マス1)$の推定値は何になるでしょうか?
1回目の探索での累積報酬和は9,10で今回は8,9,10なので$V^\pi_{t=5}(マス1)=(9+10+8+9+10)/5=9.2$になります。
同様にして$V^\pi_{t=1}(マス2)=7/1=7$になりますね。
では3回目の探索、、、
とここでこの方法ではエージェントが実際に経験した状態価値$\upsilon_\pi(マス1)$(上でいう9,10,8など)をリストなどにためておかなければならないことに気づきます。気づきますと書いてますが自分が勉強しているときは気づきませんでした、すいません。
今のように状態の種類が少ないときは大丈夫ですが、もっと莫大に状態があるときはメモリ消費が激しそうなのでどうにかしたいです。ここで推定値の計算は必ずしもリストでもつ必要はないことがわかります、どういうことかというと、
当たり前ですが平均値は合計を回数で割ったものですよね、よって
$$V^\pi_{t=T+1}(s)=\frac{TV^\pi_{t=T}(s)+G}{T+1}$$
右辺の分母はt+1回の経験で得た累積報酬和の全ての合計を表しています。それを$T+1$で割って平均値としています。
この式を使えば状態sを経験した回数と$V^\pi_{t=T}(s)$を覚えておけば状態価値の推定値の更新ができます。
しかし状態sを経験した回数も覚えなくてもよくねという方法があります、上の式より
$$V^\pi_{t=T+1}(s)=\frac{(T+1)V^\pi_{t=T}(s)+G-V^\pi_{t=T}(s)}{T+1}$$
$$=V^\pi_{t=T}(s)+\frac{1}{T+1}(G-V^\pi_{t=T}(s))$$
となります。ここの$\frac{1}{T+1}$を学習率といってこれがある条件を満たすとき$V^\pi_{t=T}(s)$は$\upsilon_\pi(s)$に収束しますが実用上は十分小さな$\alpha$を使って
$$V^\pi_{t=T+1}(s)=V^\pi_{t=T}(s)+\alpha(G-V^\pi_{t=T}(s))$$
として求めます。この辺の厳密な証明等は宿題にさせてください、すいません!!
これで回数を求める必要はなくなりましたね。
では式だけだとイメージが湧きづらいと思うので実際にコードを書いて絶対に左に行く方策のもとでの状態価値をモンテカルロ法で求めてみましょう
import numpy as np
import random
def main():
#seed固定
random.seed(0)
# 現在の推定状態価値定義
v = np.array([0., 0., 0., 0.])
# 次の推定状態価値定義
new_v = np.array([0., 0., 0., 0.])
# 報酬を定義
r = np.array([-1., -1., -1., 10.])
# 学習率alpha定義
alpha = 0.0005
# 割引率gamma定義
gamma = 1.0
# 遷移確率p定義 このpは未知であることに注意
p =1/2
# T回探索させる
T = 10000
for t in range(T):
# スタート位置を決める indexにした方が色々便利なので少しややこしいけど我慢
now_s_index = 1
#ゴールについたかの真理値定義
done = False
#経験したsを保存しておくリスト定義
experienced_s_index = []
experienced_s_index.append(now_s_index)
while not done:
#エージェントは必ず左に行くことに注意する
#1にいるときは確率pでゴール 確率1-pで元に戻る
if now_s_index == 0:
if random.random() < p:
now_s_index = 3
done = True
else:
now_s_index = 0
#2にいるときは確実に1に行く
elif now_s_index == 1:
now_s_index = 0
experienced_s_index.append(now_s_index)
experienced_s_index = np.array(experienced_s_index)
#もらった報酬取得 gave_r[0]は実際にはもらってないので注意
gave_r = r[experienced_s_index]
#経験した全てのsに対して累積報酬和計算 ただしゴールは除く
for i,s in enumerate(experienced_s_index[:-1]):
#報酬にかける割引率計算
gamma_mask = np.array([gamma**(j) for j in range(len(experienced_s_index) - (i+1))])
#累積報酬和計算
G = (gave_r[i+1:] * gamma_mask).sum()
#状態価値更新
if s == 0:
new_v[0] = v[0] + alpha*(G - v[0])
else:
new_v[1] = v[1] + alpha*(G - v[1])
v = new_v.copy()
print('v(s1):{} v(s2):{}'.format(new_v[0], new_v[1]))
'''
実行すると
p = 1/2, gamma = 1 の時
v(s1):8.973923518604037 v(s2):7.921925167076026
p = 1/4, gamma = 1 の時
v(s1):7.129079967083817 v(s2):6.005568507736658
となるはずです
'''
第1回の記事では絶対に左に行く場合マス1の状態価値は11-1/pになるという話でしたが妥当な数値が得られましたね。
1からスタートすると2を経験せずにゴールしてしまって2のサンプルが取れないので常に2からスタートするようにしてますが本当はランダムにするべきですね...
余談ですが式の感覚的な説明をしてみます。
$V^\pi_{t=T}(s)$はT回sを経験した後での推定値ですね。$G$はT+1回目のsから実際に得られた累積報酬和です。
これらの差は__「推定した状態価値より実際に得られた累積報酬和の平均はどれくらい大きいか、または小さいか」を表します、推定値と実際に得られた値との誤差__のようなものですね。
それを$V^\pi_{t=T}(s)$に加えて新たな推定値$V^\pi_{t=T+1}(s)$とするのですがいきなりその差を加えるとT+1回目の探索に寄りすぎた値になるので、__学習率$\alpha$という小さな値をかけて調整__する、というイメージです。
さて、この式に従えば今エージェントが持ってる方策の状態価値が求められます。
しかし__1つ問題があります__。それはこの方法では__ゴールにつかない限り累積報酬和が確定しないので推定値の計算ができない__というのものです。
例えばエージェントの運が悪くてマス1で左を選び続けてもマス1に帰ってくるといつまでたっても推定値の計算ができません。
他にもマス1では右、マス2では左という方策を持っていた場合、永遠にゴールに到達しないので累積報酬和の計算はいつまでもできないことになります。
これらの問題を解決するのがTD法です。息が長いですがもうひと踏ん張り!
3.TD法
モンテカルロ法は状態価値の定義
$$\upsilon_\pi(s)=E_\pi[G_t|s_t=s]$$
からスタートしましたがTD法は【強化学習】【基本編】1.MDPとベルマン方程式で導出したベルマン方程式からスタートします。
$$\upsilon_\pi(s)=\sum_{a} \Bigl(\pi(a|s)\sum_{s'}p(s'|s,a)\bigl(r(s,a,s')+\gamma \upsilon_\pi(s')\bigr)\Bigr)$$
この式は$\upsilon_\pi(s)$は次の状態s'で得られる報酬rと$\gamma\upsilon_\pi(s')$の和の期待値であることを示していると解説しました。
少し乱暴に書くとこのような感じですね。
$$\upsilon_\pi(s)=E_\pi[r+\gamma\upsilon_\pi(s')]$$
つまり__ある状態sの状態価値が知りたければ、次の状態s'で得られる報酬rと割引率をかけた状態s'の状態価値を集めて平均すれば良い__わけです。
さっきモンカルロ法ではこのような式でしたが
$$V^\pi_{t=T+1}(s)=\frac{TV^\pi_{t=T}(s)+G}{T+1}$$
今回は累積報酬和$G$の部分を$r+V^\pi_{t=T'}(s')$とすればよいですね
つまり
$$V^\pi_{t=T+1}(s)=\frac{TV^\pi_{t=T}(s)+(r+V^\pi_{t=T'}(s'))}{T+1}$$
となります。
(s'にたどり着いた時点でsを経験した回数Tとs'を経験した回数は同じとは限らないのでT'と表記しています)
モンテカルロ法のように探索でゴールに着くまで計算できないわけではなく__次の状態に進めばその時点で計算ができる__わけですね。
これならエージェントが無限ループにハマってしまっても少なくとも経験する状態に対しては状態価値が計算できます。
期待値なので何回もエージェントを動かして平均をとればよいわけですが、上のモンテカルロ法と同様に更新式は十分小さな$\alpha$を使って
$$V^\pi_{t=T+1}(s)=V^\pi_{t=T}(s)+\alpha(r+\gamma V^\pi_{t=T'}(s')-V^\pi_{t=T}(s))$$
となります。
では今回はランダムに動く方策の状態価値を実際にTD法で求めてみましょう。
import numpy as np
import random
def main():
#seed固定
random.seed(0)
# 現在の推定状態価値定義
v = np.array([0., 0., 0., 0.])
# 次の推定状態価値定義
new_v = np.array([0., 0., 0., 0.])
# 報酬を定義
r = np.array([-1., -1., -1., 10.])
# 学習率alpha定義
alpha = 0.0003
# 割引率gamma定義
gamma = 1.0
# 遷移確率p定義 このpは未知であることに注意
p =1/2
# T回探索させる
T = 100000
for t in range(T):
# スタート位置をランダムに決める indexにした方が色々便利なので少しややこしいけど我慢
now_s_index = random.choice([0,1])
next_s_index = 0
#ゴールについたかの真理値定義
done = False
while not done:
#行動をランダムに選択 -1は左 1は右
action = random.choice([-1, 1])
#0にいて左の場合は確率pでの遷移が発生
if now_s_index == 0 and action == -1:
if random.random() < p:
next_s_index = 3
done = True
else:
next_s_index = 0
#他の場合はそのまま選んだ方に移動
else:
next_s_index = now_s_index + action
if next_s_index == 3:
done = True
#もらう報酬計算
gave_r = r[next_s_index]
#更新式にしたがって計算
new_v[now_s_index] = v[now_s_index] + alpha*(gave_r + gamma*v[next_s_index] - v[now_s_index])
#更新
v = new_v.copy()
now_s_index = next_s_index
print(v)
'''
実行すると
p = 1/2, gamma = 1 の時
[6.23110256 5.79079921 7.39467171 0. ]
となるはずです
'''
第2回の記事で動的計画法で求めた際には
[6.17971198 5.77839135 7.38614297 0. ]
となっていたので概ね正しい値が得られていることがわかります。
4.終わりに
とても長くなってしまいました、お疲れ様です!
次回はSARSA, Q学習というアルゴリズムを使って、下のような強化学習を勉強しているとよく見る(?)棒を立てる問題を解いてみたいと思います!お手やわやわによろしくお願いします。

ではここまで読んでいただいてありがとうございました!
乗せてあるコードはgithubに公開しています。