この記事は【強化学習】【基本編】1.MDPとベルマン方程式の続きです。
今回もお手やわやわによろしくお願いします。
目次
0.おさらい
1.簡単な場合の状態価値の計算
2.動的計画法による状態価値の計算
3.方策反復法
4.価値反復法
5.おわりに
0.おさらい
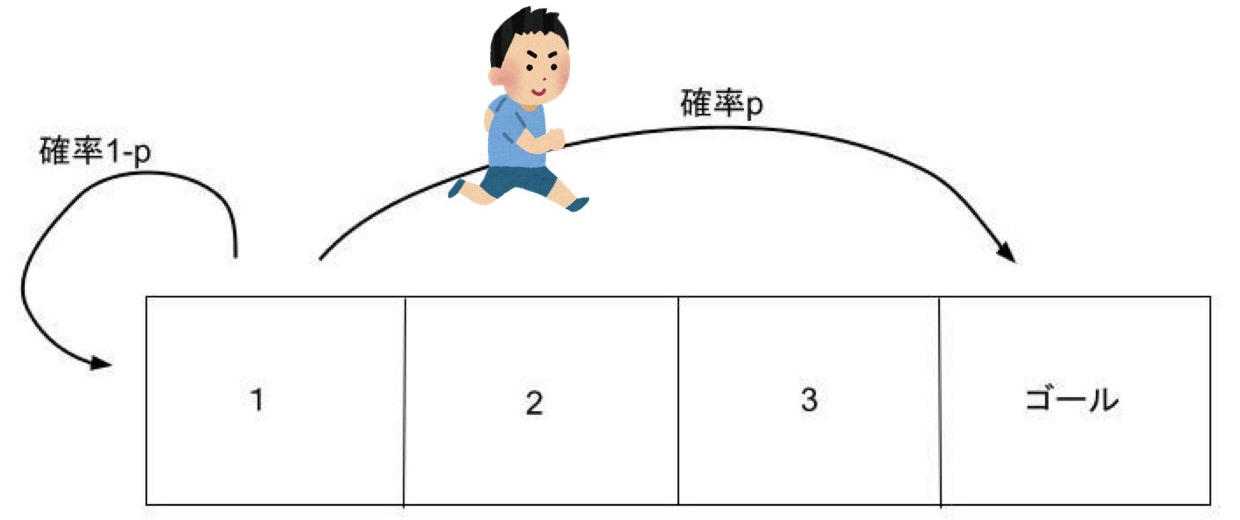
【強化学習】【基本編】1.MDPとベルマン方程式では下のようなゲームを使って、割引報酬和の説明からベルマン方程式の導出までを説明しました。
今回はベルマン方程式を使って具体的に各マスの状態価値やこのゲームでの最適な方策を求めたいと思います。
- 2,3のマスでは1回の行動で右か左に1マス動ける。1のマスから左に動くと確率pでいきなりゴールへ行けて、確率1-pで1に戻る。(普通に右に行くこともできる)
- 別のマスに移動したとき-1ポイントされるが、ゴールに到達したときは-1ポイントではなく10ポイントもらえる。1で左に行き1に戻ってきた場合も-1ポイント。
- 最初スタートする場所を1,2のどちらかから選べる。
- ゴールするまでに得たポイントの合計が高い人が勝ち
1.簡単な場合の状態価値の計算
さて、上のゲームにおいて具体的に状態価値の値を求めてみましょう。
ベルマン方程式は覚えているでしょうか、こんな式でした。
$$\upsilon_\pi(s)=\sum_a\Bigl( \pi(a|s)\sum_{s'}p(s'|s,a)\bigl( r(s,a,s')+\gamma \upsilon_\pi(s')\bigr)\Bigr) $$
状態価値関数$\upsilon_\pi(s)$は方策$\pi$の関数でもありましたね。(上のゲームで1からずっと左にいく選択をするのとずっと右にいく選択をするのでは価値が違いますよね)
ということで前回に比べた1から必ず左に行き続ける方策のもとでのマス1の状態価値と2から右に行き続けるという方策のもとでのマス2の状態価値を実際に求めて比べてみましょう
では、まずはマス2の方から行きましょう。マス2の状態価値$\upsilon_\pi (マス2)$はベルマン方程式より
(ここでの__$\pi$は絶対右に行くという方策__ということを意識してください)
$$\upsilon_\pi (マス2)=-1+\gamma \upsilon_\pi (マス3)$$
さらにマス3について考えると
$$\upsilon_\pi (マス3)=10+\gamma \upsilon_\pi (ゴール)$$
方策が確定的かつ確率的な状態遷移が無いのでベルマン方程式の$\sum_a \sum_{s'}$が現れず簡単な式になっています。
$\upsilon_\pi (ゴール)$はゴール以降から得られる収益なのでこの__ゲームのルールから$\upsilon_\pi (ゴール)= 0$となります。
よって
$$\upsilon\pi (マス2)=-1+\gamma \upsilon\pi (マス3)=-1+\gamma (10+\gamma \upsilon_\pi (ゴール))=-1+\gamma 10+\gamma^20=-1+\gamma 10$$
もちろん$\gamma =1$の時は9となって前回マス1と比べた時の数値になりますね。
続いて__絶対左に行くという方策のもとでの__$\upsilon_\pi (マス1)$を求めてみましょう。
ベルマン方程式より
$$\upsilon_\pi (マス1)=p\bigl(10+\gamma \upsilon_\pi (ゴール)\bigr)+(1-p)\bigl(-1+\gamma \upsilon_\pi (マス1)\bigr)$$
となります。右辺の$p\bigl(10+\gamma \upsilon_\pi (ゴール)\bigr)$が確率pでゴールに行けたときで$(1-p)\bigl(-1+\gamma \upsilon_\pi (マス1)\bigr)$が確率(1-p)でマス1で戻ってきた時ですね。
実際に手を動かすとベルマン方程式の意味がよく分かってくると思います。
$\upsilon_\pi (ゴール)= 0$より
$$\upsilon_\pi (マス1)=10p+-1+p+(1-p)\gamma \upsilon_\pi (マス1)$$
移項して
$$\bigl(1-(1-p)\gamma\bigr)\upsilon_\pi (マス1)=11p-1$$
よって
$$\upsilon_\pi (マス1)=\frac{11p-1}{1-(1-p)\gamma}$$
となります。
$\gamma=1$とすれば11-1/pとなってpが1/2より大きい時はマス1から始めるべきだという前回の記事の話と一致していますね。
2.動的計画法による状態価値の計算
上では行動が確定的だったので計算が簡単でしたがどのマスでもランダムに行動するという方策のとき、状態価値の計算はどのようになるでしょうか?
とりあえず各1,2,3マスについてベルマン方程式をたててみましょう。
ランダムな行動なので左右に行く確率はそれぞれ1/2ですね。
3つの式がたてれます。
$$\upsilon_\pi (マス1)=\frac{1}{2}\Bigl(p\bigl(10+\gamma \upsilon_\pi (ゴール)\bigr)+(1-p)\bigl(-1+\gamma \upsilon_\pi (マス1)\bigr)\Bigr)+\frac{1}{2}\bigl(-1+\gamma \upsilon_\pi (マス2)\bigr)$$
$$\upsilon_\pi (マス2)=\frac{1}{2}\bigl(-1+\gamma \upsilon_\pi (マス1)\bigr)+\frac{1}{2}\bigl(-1+\gamma \upsilon_\pi (マス3)\bigr)$$
$$\upsilon_\pi (マス3)=\frac{1}{2}\bigl(-1+\gamma \upsilon_\pi (マス2)\bigr)+\frac{1}{2}\bigl(10+\gamma \upsilon_\pi (ゴール)\bigr)$$
となります。
式をたててみたはいいですけどどのマスから計算すればよいでしょうか?
連立方程式を解くみたいに気合いで計算して整理したら解けそうですがかなり面倒くさそうですね。自分なら解かずに1回置いといて次の問題に行きそうです
そこで出てくるのが動的計画法です。
アルゴリズムを解説する記事ではないので詳細は他のわかりやすく書いてくださっている記事に任せるとして、大雑把にいえば簡単な問題の解からそれより少し難しい問題の解を作る方法です。賢い人へ、あってますよね?間違ってたらイジメずにご教授願います。よろしくお願いします
高校数学で$a_{n+1}=f(a_n)$という型の漸化式で表される数列の極限$\lim_{n \to \infty}a_n$を求める問題が出てきませんでしたか?
この問題には裏技のようなものがあって、_求める極限を$\alpha$とすると$\alpha=f(\alpha)$が成り立つ__はずなのでこの方程式を解いていきなり極限$\alpha$を出せるといったものです。
(例えば$a{n+1}=\sqrt{2}^{a_n}$の時、極限は$\alpha=\sqrt{2}^\alpha$を解いて2とわかります。分かるだけで高校数学の答案としてはダメです。)
これは極限$\lim_{n \to \infty}a_n$を求めるのが難しい時に方程式の解$\alpha$として求めてるわけですが、__今回は逆に解が求めにくいのでそれを極限として求めよう__という発想です。
つまり求めたい3つの状態価値を成分に持つベクトルを$\vec{v}$とすれば上の3つの連立方程式は何らかのうまい行列Aを使ってシンプルに$\vec{v}=A\vec{v}$とかけるような形になってますよね。
今この方程式を解くのが難しいという話なのですが
解である$\vec{v}$をベクトルの漸化式$\vec{v{t+1}}=A\vec{v_t}$の極限$\lim{n \to \infty }\vec{v_t}$として計算__すればよくないか?という発想です。
初項$\vec{v_1}$を適当に決めてしまってあとはプログラミングの力をかりて漸化式$\vec{v_{t+1}}=A\vec{v_t}$にしたがって$\vec{v_2},\vec{v_3},\vec{v_4},,,$と計算しほぼ値が変わらなくなるまで計算すればその値は方程式$\vec{v}=A\vec{v}$の解であり求めたかった状態価値であるということです
(理論的には無限回計算しなくてはダメですが実用上はこれでOKでしょう)
言葉で伝わり切らないところがあると思うので以下コードです
import numpy as np
def main():
# 漸化式の右辺のv定義 マスに対応していて左から1,2,3,ゴール
v = np.array([0.,0.,0.,0.])
# 漸化式の左辺のv定義
new_v = np.array([0.,0.,0.,0.])
# 報酬を定義
r = np.array([-1.,-1.,-1.,10.])
# マス1から左に行った時にゴールに行く確率 今回は1/2にした
p = 0.5
# 割引率γ定義 今回は1にした
gamma = 1.
while True:
# 漸化式からnew_vを計算
new_v[0] = 1/2*(p*(r[3]+gamma*v[3])+(1-p)*(r[0]+gamma*v[0])) + 1/2*(r[1]+gamma*v[1])
new_v[1] = 1/2*(r[0]+gamma*v[0]) + 1/2*(r[2]+gamma*v[2])
new_v[2] = 1/2*(r[1]+gamma*v[1]) + 1/2*(r[3]+gamma*v[3])
# 元のvとの誤差の合計が0.01より小さければ計算終了
if np.abs(new_v-v).sum() < 0.01:
break
print(v)
#vを更新
v=new_v.copy()
return 0
# 実行結果
'''
[0. 0. 0. 0.]
[ 1.75 -1. 4.5 0. ]
[1.6875 2.125 4. 0. ]
[3.234375 1.84375 5.5625 0. ]
[3.48046875 3.3984375 5.421875 0. ]
[4.31933594 3.45117188 6.19921875 0. ]
[4.55541992 4.25927734 6.22558594 0. ]
[5.01849365 4.39050293 6.62963867 0. ]
[5.19987488 4.82406616 6.69525146 0. ]
[5.4620018 4.94756317 6.91203308 0. ]
[5.58928204 5.18701744 6.97378159 0. ]
[5.74082923 5.28153181 7.09350872 0. ]
[5.82597321 5.41716897 7.14076591 0. ]
[5.91507779 5.48336956 7.20858449 0. ]
[5.97045423 5.56183114 7.24168478 0. ]
[6.02352913 5.6060695 7.28091557 0. ]
[6.05891703 5.65222235 7.30303475 0. ]
[6.09084043 5.68097589 7.32611117 0. ]
[6.11319805 5.7084758 7.34048795 0. ]
[6.13253742 5.726843 7.3542379 0. ]
[6.14655585 5.74338766 7.3634215 0. ]
[6.15833279 5.75498868 7.37169383 0. ]
[6.16707754 5.76501331 7.37749434 0. ]
[6.17427604 5.77228594 7.38250666 0. ]
[6.17971198 5.77839135 7.38614297 0. ]
'''
このようにしてランダムに行動するという方策でpが1/2なら、マス1からスタートした方がよいということが分かりました。
方策が決まっている時の状態価値の計算の仕方は分かりましたが、どうやって最適な方策を求めればよいでしょうか?
3.方策反復法
最適な方策を求めたいということですが、1つ浮かぶアイデアとして__右を選択したもとでの割引報酬和の期待値__と__左を選択したもとでのの割引報酬和の期待値__を比べて__大きい方の行動をする__という方策がありますね。
このような方策を__greedy方策__といいます、さらに__ある状態sにおいて行動$a$を選択したもとでの割引報酬和の期待値__は__その行動をすることの価値__であるということで__行動価値関数__といって__$q_{\pi}(s,a)$__とかかれます。状態価値関数と同じで方策$\pi$の関数でもあります。
行動価値関数は定義から
$$q_{\pi}(s,a)=\sum_{s'}p(s'|s,a)\bigl( r(s,a,s')+\gamma \upsilon_\pi(s')\bigr)$$
とかけます。ある行動をした後の報酬 $r+G_{t+1}$を次の状態$s'$で期待値をとったものですね。
ベルマン方程式は
$$\upsilon_\pi(s)=\sum_a\Bigl( \pi(a|s)\sum_{s'}p(s'|s,a\bigl( r(s,a,s')+\gamma \upsilon_\pi(s')\bigr)\Bigr) $$
だったので、$q_{\pi}(s,a)$を用いてベルマン方程式は
$$\upsilon_\pi(s)=\sum_a \pi(a|s)q_{\pi}(s,a) $$
とかけます。
_行動価値関数$q{\pi}(s,a)$は行動$a$を固定したもとでの割引報酬和の期待値__なのでそれをふまえれば当たり前ですね。
そして
1.上の動的計画法で方策$\pi$のもとでの状態価値関数$\upsilon_\pi(s)$を計算
2.その値を使って$q_{\pi}(s,a)$を計算し、ある状態sではその時に取り得る行動$a_1,a_2,,,$に対応する$q_{\pi}(s,a_1),q_{\pi}(s,a_2),,,$の各値を比較して大きい行動を選ぶという方策$\pi$に変える
の1,2を繰り返せば状態価値の数値は大きくなっていって最大化でき、そのときの方策が求めたかった最適な方策です。
(実際に示せるそうです、この数学的な証明は宿題として割愛させてください)
このような1,2を繰り返して最適な方策を求める方法を__方策反復法__といいます。
では実際にコードを書いて今まで扱ってきたゲームでの最適な方策を求めてみましょう!
import numpy as np
def main():
# 漸化式の右辺のv定義 マスに対応していて左から1,2,3,ゴール
v = np.array([0.,0.,0.,0.])
# 漸化式の左辺のv定義
new_v = np.array([0.,0.,0.,0.])
# 報酬を定義
r = np.array([-1.,-1.,-1.,10.])
# マス1から左に行った時にゴールに行く確率
p = 3/4
# 割引率γ定義 今回は1にした
gamma = 1.0
# 方策を定義 最初はランダムに動くよう初期化 pi[マスのindex,行動のindex]の値がπ(s,α)
#行動のindexは左が0で右が1 例えばpi[0,0]はマス1で左を選ぶ確率
pi = np.ones(6).reshape(3,2) * 1/2
# 更新した後の方策
new_pi = np.ones(6).reshape(3,2) * 1/2
#行動価値関数定義
q=np.zeros(6).reshape(3,2)
while True:
# 動的計画法で今のπでのvを計算
while True:
# 漸化式からnew_v計算
new_v[0] = pi[0,0]*(p*(r[3]+gamma*v[3])+(1-p)*(r[0]+gamma*v[0])) + pi[0,1]*(r[1]+gamma*v[1])
new_v[1] = pi[1,0]*(r[0]+gamma*v[0]) + pi[1,1]*(r[2]+gamma*v[2])
new_v[2] = pi[2,0]*(r[1]+gamma*v[1]) + pi[2,1]*(r[3]+gamma*v[3])
# 元のvとの誤差の合計が0.01より小さければ計算終了
if np.abs(new_v-v).sum() < 0.01:
break
# v更新
v = new_v.copy()
print('v=',v)
# 行動価値関数計算
q[0,0] = p*(r[3]+gamma*v[3]) + (1-p)*(r[0]+gamma*v[0])
q[0,1] = r[1] + gamma*v[1]
q[1,0] = r[0] + gamma*v[0]
q[1,1] = r[2] + gamma*v[2]
q[2,0] = r[1] + gamma*v[1]
q[2,1] = r[3] + gamma*v[3]
# 新しい方策計算 0で初期化
new_pi=np.zeros(6).reshape(3,2)
for state_index in range(3):
# 行動価値関数が高い行動のindex求める
a_index = np.argmax(q[state_index])
# 行動価値関数が大きかった行動をするように方策を変える
new_pi[state_index,a_index] = 1
# 元のpiとの誤差の合計が0.01より小さければ計算終了
if np.abs(new_pi-pi).sum() < 0.01:
print('best policy')
print(new_pi)
break
# pi更新
pi = new_pi.copy()
# 実行結果
'''
p=1/4としたとき
v= [4.11969305 4.40711418 6.70148673 0. ]
v= [ 6.96150913 9. 10. 0. ]
v= [ 8. 9. 10. 0.]
best policy
[[0. 1.]
[0. 1.]
[0. 1.]]
---------------------------------------------------------
p=1/2としたとき
v= [6.18412367 5.78292747 7.38919567 0. ]
v= [ 8.98900048 9. 10. 0. ]
best policy
[[1. 0.]
[0. 1.]
[0. 1.]]
---------------------------------------------------------
p=3/4としたとき
v= [7.29512794 6.52194764 7.75890793 0. ]
v= [ 9.65740284 9. 10. 0. ]
best policy
[[1. 0.]
[0. 1.]
[0. 1.]]
'''
となって確率pが1/2より大きい時はマス1からスタートした方がよいという前回の内容を裏付ける結果になりました。
(p=1/2の時はどっちも期待値が同じという結果でしたが、ほぼそうなっていることも確認できますね)
方策を更新する度に状態価値の値が上がっていっていることも確認できます。
これであなたもこのゲームでは最強です。やったね!
4.価値反復法
さてゲームの最適な方策の求め方が分かった今、何を説明するんだという感じですがまだ解説したいことがあります。
それは上の方法をもっと効率的にする方法です。
上のコードを見てもらうとよく分かりますがwhile文が2個あって効率が悪そうです。
これがなぜなのか考えると、__方策を変えるために状態価値関数を算出する__からですね。
状態価値を求めるための動的計画法をwhile文で実装していますがこれが効率が悪そうです。
ここで更新後の__方策はある行動を確率1で選択するものであるということに注目__します。
つまり状態価値関数は行動価値関数を使ったベルマン方程式より
$$\upsilon_\pi(s)=\sum_a \pi(a|s)q_{\pi}(s,a) $$
ですが、いま__方策は$q_{\pi}(s,a)$の中で値がもっとも大きい$a$を確率1で選択する__(他は0)、というものなので$\sum$内の$q(s,a)$は最大のものだけが残り結局状態価値関数は
$$\upsilon_\pi(s)=q_{\pi}(s,a^*)$$
$$a^*=argmax_a q_{\pi}(s,a)$$
とシンプルに__1つの行動価値関数__でかけます。
($argmax_xf(x)$とは$f(x)$が最大になるような$x$という意味です。)
これを使えば状態価値の算出に__動的計画法を使わなくてよいので効率が良さそう__です。
具体的には
1.行動価値関数を計算
2.方策を更新
3.上の式を使って状態価値計算
の1,2,3を繰り返すというものです。これを__価値反復法__といいます。
では同じゲームでこの方法を試してみましょう。
import numpy as np
def main():
# 漸化式の右辺のv定義 マスに対応していて左から1,2,3,ゴール
v = np.array([0.,0.,0.,0.])
# 報酬を定義
r = np.array([-1.,-1.,-1.,10.])
# マス1から左に行った時にゴールに行く確率
p = 3/4
# 割引率γ定義 今回は1にした
gamma = 1.0
# 方策を定義 最初はランダムに動くよう初期化 pi[マスのindex,行動のindex]の値がπ(s,α)
#行動のindexは左が0で右が1 例えばpi[0,0]はマス1で左を選ぶ確率
pi = np.ones(6).reshape(3,2) * 1/2
# 更新した後の方策
new_pi = np.ones(6).reshape(3,2) * 1/2
#行動価値関数定義
q=np.zeros(6).reshape(3,2)
while True:
# 行動価値関数計算
q[0,0] = p*(r[3]+gamma*v[3]) + (1-p)*(r[0]+gamma*v[0])
q[0,1] = r[1] + gamma*v[1]
q[1,0] = r[0] + gamma*v[0]
q[1,1] = r[2] + gamma*v[2]
q[2,0] = r[1] + gamma*v[1]
q[2,1] = r[3] + gamma*v[3]
# 新しい方策計算 0で初期化
new_pi=np.zeros(6).reshape(3,2)
for state_index in range(3):
# 行動価値関数が高い行動のindex求める
a_index = np.argmax(q[state_index])
# 行動価値関数が大きかった行動をするように方策を変える
new_pi[state_index,a_index]=1
# 元のpiとの誤差の合計が0.01より小さければ計算終了
if np.abs(new_pi - pi).sum() < 0.01:
for state_index in range(3):
v[state_index] = q[state_index].max()
print('v=',v)
print('best policy')
print(new_pi)
break
# pi更新
pi = new_pi.copy()
#状態価値関数計算 あるsでq(s,a)の最大値であることに注目
for state_index in range(3):
v[state_index] = q[state_index].max()
print('v=',v)
# 実行結果
'''
p=1/4としたとき
v= [ 1.75 -1. 10. 0. ]
v= [ 3.0625 9. 10. 0. ]
v= [ 8. 9. 10. 0.]
v= [ 8. 9. 10. 0.]
best policy
[[0. 1.]
[0. 1.]
[0. 1.]]
----------------------------------------
p=1/2としたとき
v= [ 4.5 -1. 10. 0. ]
v= [ 6.75 9. 10. 0. ]
v= [ 8. 9. 10. 0.]
v= [ 8.5 9. 10. 0. ]
v= [ 8.75 9. 10. 0. ]
best policy
[[1. 0.]
[0. 1.]
[0. 1.]]
----------------------------------------
p=3/4としたとき
v= [ 7.25 -1. 10. 0. ]
v= [ 9.0625 9. 10. 0. ]
v= [ 9.515625 9. 10. 0. ]
best policy
[[1. 0.]
[0. 1.]
[0. 1.]]
'''
となって方策反復法のときと同じ方策が得られました。
5.おわりに
お疲れ様でした。かなりハードな内容で頑張ったつもりですが分かりにくにところもあるかもしれません、ぜひコメントで教えてください。
ここまで読んでいただいてありがとうございました!!
乗せてあるコードはgithubに公開しています。