BoTorch 実践4. 制約付きベイズ最適化

---

BoTorch 入門 1.
BoTorch 入門 2.
BoTorch 入門 3.

BoTorch 実践 3. ノイズの扱い
BoTorch 実践4. 制約付きベイズ最適化

---

BoTorch実践シリーズ　制約付き最適化です。多目的ではありません。

BoTorchの制約には以下の二通りがあります。

制約はBoTorchではParameter ConstraintsとOutcome Constraintsの２つに分けられます。
Parameter Constraintsはいわゆる等式制約や不等式制約のことで、これらは獲得関数の最大化を行うscipy.optimize.minimizeへ適用されます。Outcome Constraintsはベイズ最適化特有の制約で、別のブラックボックス関数の出力への制約です。
制約付きのベイズ最適化手法は数多く提案されていますが、BoTorchではProbability of Feasibilityという手法を採用しています。

こちらを実験していきます
最適化のテスト関数としてよく知られるBranin関数を用います。こんな感じの関数です。

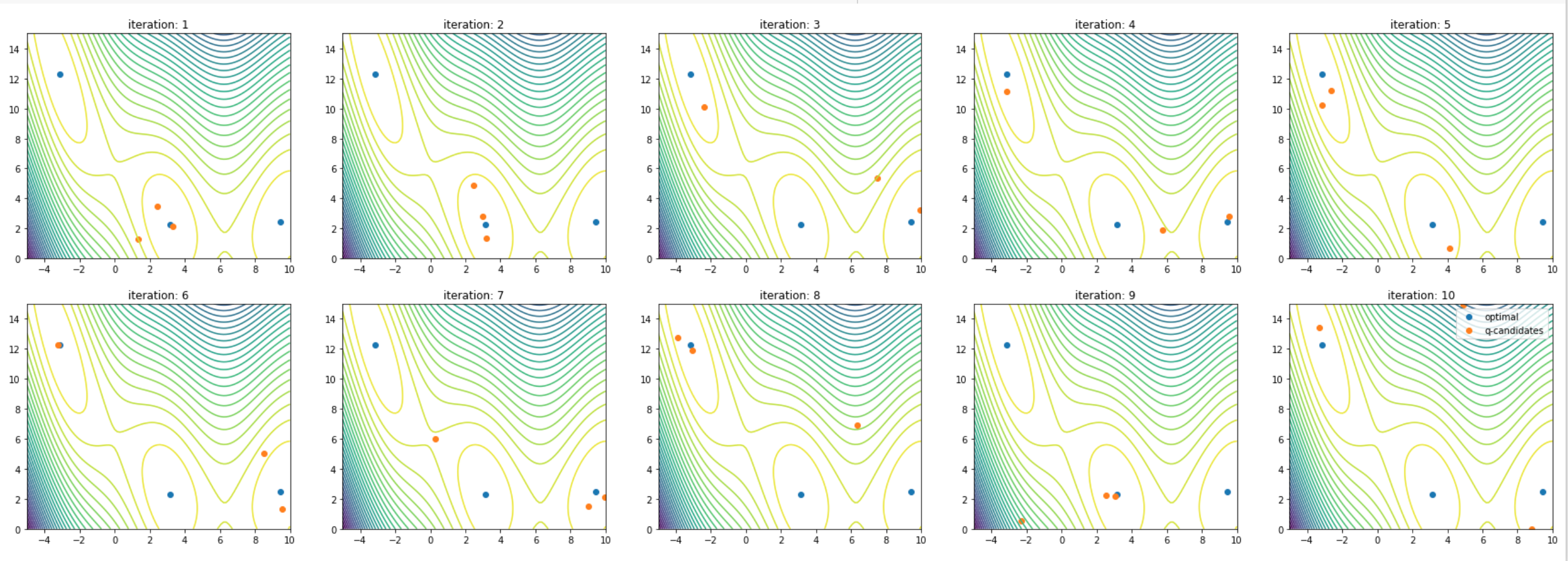
まずはじめに制約がない通常の最適化をやってみます。
獲得関数はqEI(q=3)を用いました。

from botorch.test_functions import Branin
import torch

func = Branin(negate=True)
bounds  = torch.tensor([[-5.,0.],[10.,15.]])
train_X = bounds[0].unsqueeze(0) + (bounds[1] - bounds[0]) * torch.rand(5,2,dtype=torch.float64)
train_y = func(train_X).unsqueeze(-1)

from botorch.models import SingleTaskGP
from gpytorch.mlls import ExactMarginalLogLikelihood
from botorch import fit_gpytorch_mll
from botorch.optim import optimize_acqf
from botorch.acquisition import qExpectedImprovement

iteration = 10
for iter in range(1,iteration+1):
    model = SingleTaskGP(train_X,train_y)
    mll = ExactMarginalLogLikelihood(model.likelihood,model)
    fit_gpytorch_mll(mll)

    qEI = qExpectedImprovement(model, train_y.max())

    candidates, _ = optimize_acqf(qEI,bounds=bounds,q=3,num_restarts=16,raw_samples=128)
    train_X = torch.cat([train_X,candidates],dim=-2)
    train_y = torch.cat([train_y, func(candidates).unsqueeze(-1)],dim=-2)

結果はこんな感じになりました

割と早いiteraionで最適解にたどり着いているように見えます。
これに制約を加えていきましょう

Parameter Constraints

Parameter Constraintはoptimize_acqfで指定します
どのような制約が適応可能かというと

• inequality_constraints: Optional[List[Tuple[Tensor, Tensor, float]]]
  A list of tuples (indices, coefficients, rhs),with each tuple encoding an inequality constraint of the form \sum_i (X[indices[i]] * coefficients[i]) >= rhs

  x[0] - 2 * x[1] < -6としたいとすると,
  inequality_constraints = [(torch.tensor(0,1), torch.tensor(1.,-2.),6)]ということですね。不等式制約が複数ある場合も同様にタプルを追加していけば良さそうです。

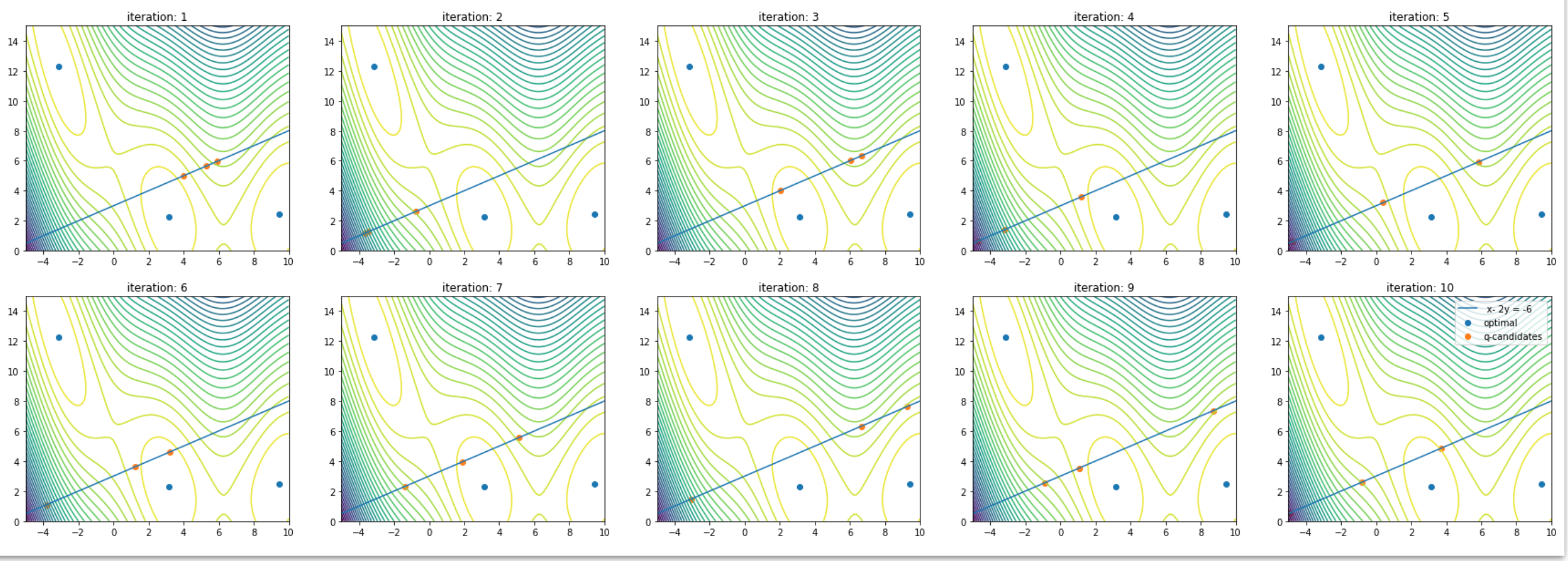
やってみましょう
変更するのは一部だけです。

    candidates, _ = optimize_acqf(    
                        qEI,
                        bounds=bounds,
                        q=3,
                        num_restarts=16,
                        raw_samples=128,
                        inequality_constraints= [(torch.tensor([0,1]),torch.tensor([1.,-2.]),-6.0)]
                    )

期待通り指定した領域のみで最適化が行われたようです

等式制約も同様です

• equality_constraints: Optional[List[Tuple[Tensor, Tensor, float]]]
  A list of tuples (indices, coefficients, rhs), with each tuple encoding an equality constraint of the form \sum_i (X[indices[i]] * coefficients[i]) = rhs

    candidates, _ = optimize_acqf(    
                        qEI,
                        bounds=bounds,
                        q=3,
                        num_restarts=16,
                        raw_samples=128,
                        equality_constraints= [(torch.tensor([0,1]),torch.tensor([1.,-2.]),-6.0)]
                    )

最後は非線形な不等式制約です

• nonlinear_inequality_constraints: Optional[List[Callable]]
  A list of callables with that represent non-linear inequality constraints of the form callable(x) >= 0. Each callable is expected to take a (num_restarts) x q x d-dim tensor as an input and return a (num_restarts) x q-dim tensor with the constraint values. The constraints will later be passed to SLSQP. You need to pass in batch_initial_conditions in this case. Using non-linear inequality constraints also requires that batch_limit is set to 1, which will be done automatically if not specified in options.

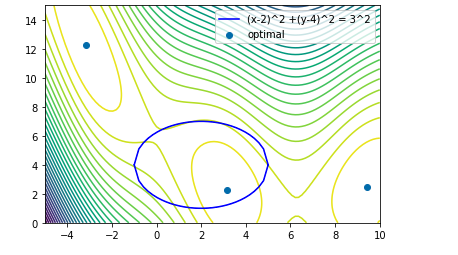
例えば円の内側という制約を考えてみましょう.以下のような感じです

nonlinear_inequality_constraintsは[lambda x: -(torch.sum((x - torch.tensor([2,4]))**2,dim=-1) - 9)]というふうにすれば問題ないはずです。引数xの形状がが(num_restarts) x q x dであることに注意しましょう.

加えてbatch_initial_conditionsが必要らしいです。batch_initial_conditionsは獲得関数の最適化の初期点であり、形状は(num_restarts) x q x dです。非線形な制約のため初期点を決定できないためこちらで指定する必要があるようです。適当に円の中心付近のデータを与えてやりましょう。

これで行けるかと思いましたが、、、あまりうまく行きません。
まず、q=1じゃないとエラーが出ます。それと最適化がうまく進みません。

    candidates, _ = optimize_acqf(   
                                  qEI,
                                  bounds=bounds,
                                  q=1,
                                  num_restarts=16,
                                  raw_samples=128,
                                  nonlinear_inequality_constraints= [lambda x: -(torch.sum((x - torch.tensor([2,4]))**2,dim=-1) - 9)],
                                  batch_initial_conditions=torch.tensor([0.,3,])+torch.rand(16,1,2).to(train_X),
                                  )

まだ新しい機能ということもあってか色々問題があるんでしょうか。。

Outcome Constraint

制約もまたブラックボックス関数という状況で用いられるものです。
Outcome ConstraintにはConstraintMCObjectiveを利用するのがBoTorchでは一般的だと思います。BoTorchにおいてObjectiveは出力を変換させるような働きを持ちますが、Outcome Constraintでは出力に制約を掛けるという変換を行います。

今回は先程と同様の円の内部での最適化を考えましょう。
中心(6,4),半径3の円です.

from botorch.test_functions import Branin
import torch

func = Branin(negate=True)
bounds  = torch.tensor([[-5.,0.],[10.,15.]])
train_X = bounds[0].unsqueeze(0) + (bounds[1] - bounds[0]) * torch.rand(15,2,dtype=torch.float64)
train_y = func(train_X).unsqueeze(-1)

制約関数を準備します。戻り値が0以下である制約を考えるため、

def constraint(X):
  return (torch.sum((X - torch.tensor([6,4]))**2,dim=-1) - 9)

とします。Xはb x q x dという形状で与えられるはずなので注意しましょう。

ここでConstrainedMCObjectiveを

from botorch.acquisition.objective import ConstrainedMCObjective

# define a feasibility-weighted objective for optimization
constrained_obj = ConstrainedMCObjective(
    objective=lambda Z: Z[..., 0],
    constraints=[lambda Z: Z[..., 1]],
)

と定義します。なぜこうするのかは色々と内部の実装が関わってくるため細かいことは飛ばします。

ただ、↓で定義するように今回使うモデルはModelListGP(model_obj, model_constraint)となっており、0番目が対象の関数に、1番目が制約関数であることをZ[..., 0]などで伝えている感じです。

from botorch.models import SingleTaskGP,ModelListGP
from gpytorch.mlls import ExactMarginalLogLikelihood,SumMarginalLogLikelihood
from botorch import fit_gpytorch_mll
from botorch.optim import optimize_acqf
from botorch.acquisition import qExpectedImprovement

iteration = 12
plt.figure(figsize=(20,20))
for iter in range(1,iteration+1):
    model = SingleTaskGP(train_X,train_y)  
    model_c= SingleTaskGP(train_X,train_c) #制約関数をモデリングする

    models = ModelListGP(model, model_c)  #複数のモデルを扱うためModelListを使う
    mll =SumMarginalLogLikelihood(models.likelihood,models)
    fit_gpytorch_mll(mll)  #modelとmodel_cのハイパーパラメータの最適化

    #qEIに与えるbest_fは制約を満たした上での最大値であることに留意

    #(train_y * (train_c <= 0)).max()というのはmodelとmodel_cの学習データが同一だから大丈夫
    #例えば制約のmodel_cは別に学習データがある場合なども考えられる

    qEI = qExpectedImprovement(models, (train_y * (train_c <= 0)).max(),objective=constrained_obj)

    candidates, _ = optimize_acqf(   
                                  qEI,
                                  bounds=bounds,
                                  q=3,
                                  num_restarts=16,
                                  raw_samples=128, 
                                  )
    train_X = torch.cat([train_X,candidates],dim=-2)
    train_y = torch.cat([train_y, func(candidates).unsqueeze(-1)],dim=-2)
    train_c = torch.cat([train_c, constraint(candidates).unsqueeze(-1)],dim=-2)
    plt.subplot(3,4,iter)
    plt.title(f"iteration: {iter}")
    plot_contour(func,bounds.numpy(),candidates=candidates,show=False)

    plt.legend()
plt.show()

それになりにできていそうですね。最適化とともに円の内部に探索点が集中していってます。

制約が複数ある場合は、同様に制約の数だけmodelを構築してModelListGPに入れることと、
ConstrainedMCObjectivesを

constraints = []
for i in range(constraint_num):
    constraints.append(lambda Z, i=i: Z[..., 1 + i])

constrained_obj = ConstrainedMCObjective(
    objective=lambda Z: Z[..., 0],
    constraints=constraints,
)

とすれば問題ないでしょう。

[補足]　内部の実装について

ConstrainedMCObjectiveのところで飛ばしたところを丁寧に見てみます。
ただモンテカルロ獲得関数の実装を前提としているところがあります。ご了承ください。

ConstrainedMCObjectiveが利用されるのは獲得関数の近似のところです。
qEIの実装を見てみます。

qEI.py

    @concatenate_pending_points
    @t_batch_mode_transform()
    def forward(self, X: Tensor) -> Tensor:
        r"""Evaluate qExpectedImprovement on the candidate set `X`.
        Args:
            X: A `batch_shape x q x d`-dim Tensor of t-batches with `q` `d`-dim design
                points each.
        Returns:
            A `batch_shape'`-dim Tensor of Expected Improvement values at the given
            design points `X`, where `batch_shape'` is the broadcasted batch shape of
            model and input `X`.
        """
        posterior = self.model.posterior(
            X=X, posterior_transform=self.posterior_transform
        )
        samples = self.get_posterior_samples(posterior)
        obj = self.objective(samples, X=X)
        obj = (obj - self.best_f.unsqueeze(-1).to(obj)).clamp_min(0)
        q_ei = obj.max(dim=-1)[0].mean(dim=0)
        return q_ei

        obj = self.objective(samples, X=X)

このself.objectiveがConstrainedMCObjectiveインスタンスですね。

上から見ていくと、

• posterior - Xにおけるmodelの事後分布. このmodelはModelListGPだと想定されるため制約のガウス過程も含めた事後分布(ModelListGPの事後分布は、MultiTaskGPのタスク間が独立なものとして実装されている.)
• samples - posteriorからのサンプル. 形状はsample_size x b x q x mという高階のテンソル
  • sample_size - モンテカルロ方のサンプルサイズ
  • b - (t-)batchのサイズ. num_restartかbatch_limit.
  • q - (q-)batchのサイズ.
  • m - 出力の数. [関数fのサンプル, 制約1のサンプル, ... , 制約m-1のサンプル] といった感じ

ConstrainedMCObjective.py

def forward(self, samples: Tensor, X: Optional[Tensor] = None) -> Tensor:
        r"""Evaluate the feasibility-weighted objective on the samples.
        Args:
            samples: A `sample_shape x batch_shape x q x m`-dim Tensors of
                samples from a model posterior.
            X: A `batch_shape x q x d`-dim tensor of inputs. Relevant only if
                the objective depends on the inputs explicitly.
        Returns:
            A `sample_shape x batch_shape x q`-dim Tensor of objective values
            weighted by feasibility (assuming maximization).
        """
        obj = super().forward(samples=samples)
        return apply_constraints(
            obj=obj,
            constraints=self.constraints,
            samples=samples,
            infeasible_cost=self.infeasible_cost,
            eta=self.eta,
        )

この

    obj = super().forward(samples=samples)

は以下で指定したobjectiveです.つまり,objにはsamples[... , 0], $f$に対するサンプルが入ります。

 ConstrainedMCObjective(
    objective=lambda Z: Z[..., 0],
    constraints=constraints,
)

apply_constraintsは以下のようになっています(一部改変)

    obj = obj.add(infeasible_cost) 

    obj = obj.clamp_min(0)  # Enforce non-negativity with constraints
    for constraint, e in zip(constraints, eta):
        constraint_eval = torch.sigmoid(-constraint(samples) / eta)
        obj = obj.mul(constraint_eval)

    obj.add(-infeasible_cost)

    return obj

objが$f$のサンプル値であり、objにconstraint_evalをかけています。このconstraint_evalは制約関数のGPからサンプリングした値で、Probability of feasibilityをシグモイド関数で近似しているようです。

注意すべきがobj.clamp_min(0)です。BoTorchのProbability of Feasibilityの実装は制約を満たす確率を掛けることでその点の探索に制限をかけます。しかしその値が負であった場合この理論は成り立たちません。簡単に言うと、負の値を取りうる関数の制約付き最適化は失敗しかねません。その対策としてinfeasible_costというパラメータが準備されています。自分も使い方が完全にわかっているわけではないですが、例えば負の値をとる関数の制約付き最大化で利用することが推奨されていたりします。