BoTorch 入門 1.
BoTorch 入門 2.
BoTorch 入門 3.
BoTorch 実践 3. ノイズの扱い
BoTorch 実践4. 制約付きベイズ最適化
はじめに
今回も公式ドキュメントに基づきBoTorchの基本事項を説明します。定義がややこしかったり、ベイズ最適化の理論と密接だったりするので自分の知識整理用でもあります。
ガウス過程やベイズ最適化の基本はwebに多く存在するのでそちらに譲ります。おすすめの論文や関連論文はこちらにおいてます。
コンセプト
BoTorchのコンセプトは以下の図の通りです。公式Docからとってきてます。
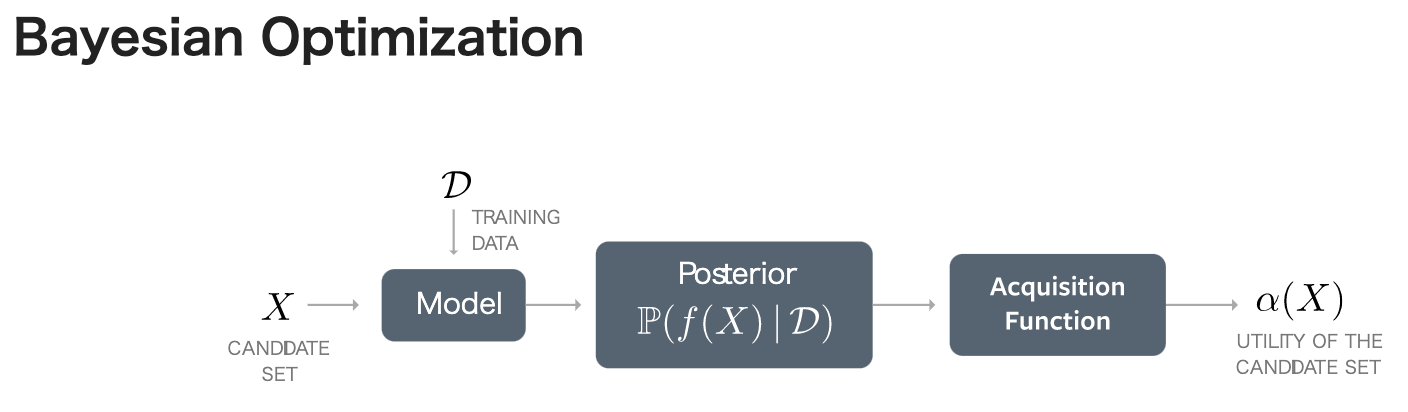
| Model | 基本はGPyTorchのModelをベースとしていますが、BoTorchでは目的や状況に応じた複数のModelが用意されています。 |
| Posterior | BoTorch上では入力$X$に対する事後分布クラスです。model.posterior(X)の返り値としてposteriorインスタンスを受け取ることができます。 |
| Acquisition Function | EI,PIなど基本的なものからqNEI,MES,qKG,qEHVIなど多様な獲得関数が実装されています。BoTorchでは解析的な表現をもつanalyticな獲得関数と近似が必要なmonte-carlo獲得関数に分けられます。 |
最適化の流れをこの図にそって説明すると、
- 学習データ$D$をmodelに与えてガウス過程を学習させます。
- 初期候補点$X$でのposteriorをmodelを通じて得ます。
- 一般に獲得関数はガウス過程の事後分布による期待値として与えられることが多いため,
- monte-carlo獲得関数: その事後分布からサンプリングを行い獲得関数の値を(準)モンテカルロ近似します
- analytic獲得関数: そのまま普通に計算します。
- 自動微分により$X$についての勾配を計算し、準ニュートン法などで最大化します
- 最大化によって得られた$X_{new}$を目的の関数$f$で評価して$y_{new}$を観測する
- $D_{new} = D \cup \lbrace X_{new},y_{new} \rbrace $として、1に戻る
用語解説
ガウス過程やベイズ最適化の基礎は知っているものと仮定しますが、いくつかわかりにくいトピックについて簡単に説明を加えていきます。
ベイズ最適化関連
HyperParameterの最適化
カーネルに内在するハイパーパラメータを勾配法などを使って最適化することです。ガウス過程では周辺尤度が解析的に求まることを利用しています。また、MCMCによりハイパーパラメータのサンプルを持っておく方法もありますがBoTorchでは一部のModelでしか対応していません。
Multi-〇〇 Bayesian Optimization
最適化は問題の設定によって細かな違いがあるため気をつけなければなりません。
それぞれ微妙な差異があり、わかりにくいため[1]を参考に表にまとめます。
| Multi Task Bayesian Optimization(MTBO) | 複数の関数を最適解を同時に探索する。各関数に関連がある場合に学習を効率的に行うことができる。 |
| Multi Objective Bayesian Optimization(MOBO) | 複数の目的関数を最適化する一つの解を探索する。パレート最適を求める. |
| Multi Fiedlity Bayesian Optimization(MFBO) | 評価にコストの掛かる関数の代わりに、コストが低くかつ本来の関数と似た振る舞いをする関数を利用することで効率的に最適化を進める手法。 |
| Transfer/Meta Learning | 他の関連する関数の最適化の結果を利用することで別の関数の最適化を効率よく進める手法。[1]によれば、ベイズ最適化においてはTransfer /Meta Learning は用語として交換可能。 |
[1]によるとMFBOはMTBOの一部とみなせることも可能です。MTBOはすべてのタスクの最適化が目的でしたがMFBOは一つの関数の最適化が対象です。
ただ正直この分け方は曖昧です。今回は[1]に従っていますが、論文中にも
(MFBOの説明)
This is known as multi-fidelity optimization (MFO), which can be seen as a subclass
of multi-task learning, where the group of related functions can be
meaningfully ordered by their similarity to the objective funct
(Transfer/Meta Learningの説明)
Note that in the Bayesian optimization community, knowledge transfer has also been investigated under the several umbrellas, including multi-task learning and multi-fidelity optimization, which may overlap with the broad field of transfer learning.
とあり、明確に住み分けられているわけではありません。
またMTBOでよく参照される[2]では、MTBOの例としてMLのハイパラチューニングを、小規模のデータセットによる最適化結果を大規模なデータセットの最適化に利用することを上げていますがこれはMFBO/Transfer/Meta Learningのように思えます。
他のややこしい点として、BoTorchではMultiTaskBayesian Optimizationという用語はドキュメントやソースコードに出てきません。用意されているのはMultiTaskGaussianProcess(MTGP)であり、タスク間の相関をモデリングすることはできますが、MTBOとして準備されているわけではありません。例えば、MOBOのときに目的関数同士に相関があるなしでMTGPを使うか使わないか分けているような感じです。MFBOに関してはMulti Fidelity用のモデルがある他、KroneckerMultiTaskGP等が準備されているようです。
[1]Wang, Xilu et al. "Recent Advances in Bayesian Optimization." ArXiv abs/2206.03301 (2022): n. pag.
[2]Kevin Swersky, et al. "Multi-task Bayesian optimization." In Proceedings of the 26th International Conference on Neural Information Processing Systems - Volume 2 (NIPS'13).
Batch Bayesian Optimization
バッチベイズ最適化は最適化をparallelに行う手法です。たとえばシミュレーション環境が複数あれば複数の異なるパラメータを同時に実行できます。これは獲得関数から次の探索点を複数生成することで実現できます。
いろいろな手法が提案されていますが、BoTorchではq-〇〇(〇〇は獲得関数の名前)として定義された獲得関数を用います。
qEI, qUCB,qKGなどがあり、q個の候補点を生成することができます。ただこれらはモンテカルロ近似によって求める必要があるため、BoTorchではこれらの獲得関数をMonte-Carlo獲得関数と呼称しています。
ただ紛らわしいことにBoTorchは行列演算のメリットを享受するため機械学習などの文脈でのBatchも使います。例えばqEIといった獲得関数の入力の形状はbatch_shape x q x dです。batch_shapeは機械学習の文脈でのbatchであり、qは獲得関数の意味でのBatchです。ちなみにdは関数の次元です。これによりbatch_shape個のqEIの値をまとめて評価できるのですが非常にややこしいです。そのためBoTorchでは機械学習の文脈でのbatchをt-batch,獲得関数の意味でのBatchをq-batchとよんでいます。
BoTorch関連
Noise
Botorchでは観測ノイズの扱い方が3種類あり、HomoskedasticとFixedとHeteroskedasticと分けられます。
-
Homoskedasticではノイズはハイパーパラメータの最適化として推論されます。このノイズは入力に関わらずどこでも同一のノイズが加わっているものとしてモデリングされます。 -
Fixedではノイズは陽に与えられます。つまり例えば出力のノイズが何らかの方法でわかっている場合、入力と出力と観測ノイズの情報を渡すことでモデリングの精度を高めることに繋がります。ノイズはどの地点でも同一である必要はなく、逆にどの地点でもほとんど0とすることでノイズが無いとモデルに伝えることができます。ただ未知の入力点に対するノイズはわからないため未知の入力点での事後分布にはノイズの情報は含まれません -
HeteroskedasticではFixedと同様にノイズの情報が陽に与えられますが、入力とノイズの関係性を新たなガウス過程でモデリングするため、未知の入力点に対してもノイズを含んだ結果を返すことが可能です。
Sampler
Monte-Carlo獲得関数の計算にはモンテカルロ近似を必要としますが、モンテカルロ法は収束の遅さがボトルネックとなります。ここでBoTorchではシンプルなモンテカルロ法ではなく準モンテカルロ法を利用しています。デフォルトではRandomized Sobol'列を生成するSamplerクラスが使用されますがこれらはカスタマイズすることも可能です。例えば通常の一様乱数を用いた方法や、LatinHyperCubeを使用することも可能です。
Multi Start Optimization
獲得関数の最大化にはL-BFGS-B法が用いられていますが実装では複数の初期点より最適化を行います。
これは獲得関数が多くのところで0となってしまうため、値が0のところから最適化を始めることを避けるための手段です。初期点の決め方はraw_samples個の候補点よりnum_restart個をヒューリスティックに決定します。
論文のAppendix F.1で言及されており、実装はここのinit_funcで行われます。
これらはoptimize_acqf関数の引数であるnum_restartとraw_samplesで指定します。
Constraints
制約はBoTorchではParameter ConstraintsとOutcome Constraintsの2つに分けられます。
Parameter Constraintsはいわゆる入力の等式制約や不等式制約のことで、これらは獲得関数の最大化を行うscipy.optimize.minimizeにそのまま渡されます。
Outcome Constraintsはベイズ最適化特有の制約で、制約関数もまたブラックボックス関数です。
制約付きのベイズ最適化手法は数多く提案されていますが、BoTorchでは「Probability of Feasibility」という手法を採用しています。