高次元ベイズ最適化は1行追加で精度が上がるかもしれない

Last updated at 2024-10-23Posted at 2024-07-30

株式会社Enginee取締役・エンジニアの@__Kat__です。最近日傘買いました。

TL;DR

高次元でのベイズ最適化は多くの手法があるが、ハイパーパラメータ一つ変更するだけで十分精度が出るかもしれない

ガウス過程ベースのベイズ最適化の話です。OptunaでTPEとか使ってる場合は関係ないです。

2024/09/19追記

BoTorchのv0.12でデフォルトの事前分布として追加されたようです

ベイズ最適化

ベイズ最適化は基本的に

関数のモデリング
獲得関数を最適化して次の探索点を決定する
を繰り返します。

モデリングはガウス過程やTPE(Optuna)が有名ですが、決定木やBNNなどの例もあります。

ガウス過程

学習データ$(X_{1,n},y_{1:n})$があったとき、ガウス過程の事後分布は次式で表現できます。

\boldsymbol{f}^*| X_{1:n},\mathbf{y}_{1:n},X^* \sim N(\boldsymbol \mu_n(X^*),V_n(X^*))

\displaylines{
 \boldsymbol \mu_n(X^*) &= V(X^*,X_{1:n})(V(X_{1:n},X_{1:n})+\sigma^2I)^{-1}(\mathbf{y}_{1:n}) - \boldsymbol \mu(X_{1:n})) + \boldsymbol \mu(X^*)\\
    V_n(X^*) &= K(X^*,X^*) - K(X^*,X_{1:n})(K(X_{1:n},X_{1:n})+\sigma^2I)^{-1}K(X_{1:n},X^*)
}

獲得関数は最も一般的なものはExpected Improvementであり、とくにガウス過程を用いた場合は以下のように解析的に計算できます。

\begin{align}
a_{EI}(\mathbf{x}) &= \mathbb{E}[(y-y^*)^+| x_{1:n},y_{1:n}]\\
&= \left ( \mu(\mathbf{x}) - y^*\right )\Phi(Z) + \sigma(\mathbf{x})\phi(Z)
\end{align}

ガウス過程のハイパーパラメータは、例えばRBFカーネルなら以下の$\theta_0,\theta_1,\theta_2$となります。
ARDを利用する場合は次元毎に$\theta_1$(lengthscale)が設定されるため、ハイパーパラメータもその分増えます。

k(x,x') = \theta_0 exp(-  \frac{||x-x'||^2}{\theta_1}) + \theta_2

このハイパーパラメータは手動で決める必要があるように見えますが、周辺尤度が計算できるため勾配法を用いて最適化可能です。一般的にハイパーパラメータはMLE, MAP, MCMCのいずれかで決定されます。BoTorchはデフォルトではMAP推定が採用されています。

高次元

ベイズ最適化は一般的に20次元程度までしか使えない、などと言われます。次元が大きくなるとガウス過程のフィッティングの精度が下がると同時に、獲得関数の最適化がうまく進まないからです。

　そのため高次元でも最適化が上手く進むような研究がされているのですがベストプラクティスがあるわけではなく、多くの手法が登場した結果高次元に特化したサーベイ論文も最近出ているほどです。¹

図を見ると分かる通り、魔境と化しています。

このサーベイ論文では、手法を

Variable selection
Additive Models
Trust regions
Linear embeddings
Non-Linear embeddings
Gradient information
Structured Space
Other

というふうに分類しています。

この中のAdditive Modesl, Trsut Region, Embeddingsといった手法は松井先生の資料を参考にしていただけるとよく分かるかと思います。²

そして、Otherで取り上げられている2つの論文では、通常のガウス過程、もしくは軽微な修正で十分に性能が出ると報告されています。³⁴

本題

今回はこの内のVanilla Bayesian Optimization Performs Great in High Dimensionsを実装してみます。
この論文はすでに検証記事もあるので、こちらを参考にしてもいいです⁵。

この論文では、学習時のlengthscaleの事前分布に対数正規分布をおいてMAP推定しろといっています。
(Dは次元の数。)
$$
l \sim LogNormal(\mu_0 + \frac{1}{2}\log{D}, \sigma_0)
$$

これをBoTorchで実装します。
BoTorchでは何も指定しない場合、MaternKernel + ARDが用いられ、lengthscaleの事前分布にGamma分布をおいてMAP推定しています。

そのためこれをLogNormalに変えればいいです。

gp = SingleTaskGP(
    train_X=data_X,
    train_Y=data_y,
    train_Yvar=1e-5 * torch.ones_like(data_y),
    input_transform=Normalize(d=dim),
    outcome_transform=Standardize(m=1),
    # ---- 追加 --- 
    covar_module=ScaleKernel(
        base_kernel=MaternKernel(
            nu=2.5,
            ard_num_dims=dim,
            # -----   本質的な変更点はここだけ   ------
            lengthscale_prior=LogNormalPrior(mu_0 + np.log(dim)/ 2, sigma_0),
        ),
        outputscale_prior=GammaPrior(2.0, 0.15),
    )
)

mll = ExactMarginalLogLikelihood(gp.likelihood, gp)
fit_gpytorch_mll(mll)

検証

検証ブログと同様に、いかの関数を設定する($\boldsymbol{r}$は適当な一様乱数)
$$
f_\boldsymbol{r}(\boldsymbol{x}) = \sum(x_i - r_i)^2
$$

次元数を64
初期の学習データ数を500
としたとき、ランダムにサンプリングした100個の点を予測させます。

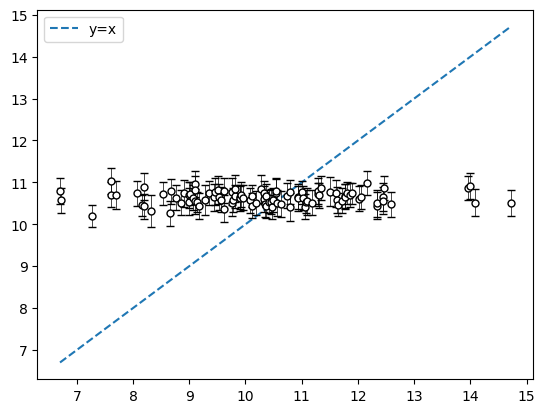
通常のガウス分布によるフィッティング

横軸が真の値、縦軸が予測値

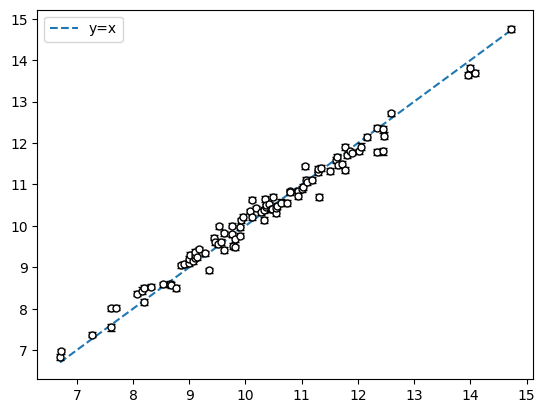
対数正規分布を利用したガウス分布によるフィッティング

横軸が真の値、縦軸が予測値

ずいぶんとフィッティングの精度が上がりました。

この流れでベイズ最適化もしました

通常のガウス分布によるベイズ最適化

横軸がiteration、縦軸がその地点での最大値、95%CI

対数正規分布を利用したガウス分布によるベイズ最適化

横軸がiteration、縦軸がその地点での最大値、95%CI

コードの一部

# ベイズ最適化
dim = 64
r = torch.rand(dim,dtype=torch.float64).to(device)

initial_points_num = 500
iter_num=10
func = f
sample_num =100
sample_point_num = 100
bounds = torch.stack([torch.zeros(dim), torch.ones(dim)]).to(torch.double).to(device)

batch = 10

def f(X):
  """
  function f = \sum (x_i-r_i)^2
  """
  d = X.shape[-1]
  return torch.sum((X-r)**2,dim=1)

  
all_best = []
for _ in tqdm_notebook(batch):
  initial_X = torch.rand([initial_points_num,dim],dtype=torch.float64).to(device)
  initial_y = func(initial_X).unsqueeze(1)

  train_X = initial_X
  train_y = initial_y
  best = [train_y.max().item()]

  for i in tqdm_notebook(range(iter_num)):
    gp = SingleTaskGP(
      train_X=train_X,
      train_Y=train_y,
      input_transform=Normalize(d=dim),
      outcome_transform=Standardize(m=1),
    )
    # gp.covar_module.base_kernel.lengthscale_prior = LogNormalPrior(mu_0 +np.log(n_dim)/2, sigma_0)

    mll = ExactMarginalLogLikelihood(gp.likelihood, gp)
    fit_gpytorch_mll(mll)
    # EI -> logEIが推奨されている
    logEI = LogExpectedImprovement(model=gp, best_f=train_y.max())
    candidate, acq_value = optimize_acqf(
      logEI, bounds=bounds, q=1, num_restarts=5, raw_samples=50,
    )

    y = func(candidate).unsqueeze(0)

    train_X = torch.cat([train_X, candidate], dim=0)
    train_y = torch.cat([train_y, y], dim=0)

    best.append(train_y.max().item())
  all_best.append(best)



plt.errorbar(range(iter_num+1), np.mean(all_best,axis=0), yerr=1.96 * np.std(all_best,axis=0) / np.sqrt(batch))
plt.show()

# 事後分布からのサンプル部分
pred = gp.posterior(X).sample(torch.Size([sample_num]))
pred= pred.squeeze(-1)
mean = pred.mean(0)
ci = 1.96 * pred.std(0) / np.sqrt(sample_num)

values = torch.stack([y,mean,ci],dim=1).detach().numpy()
values = values[np.argsort(values[:,0])]

## plot y = x
plt.plot(values[:,0],values[:,0],linestyle="dashed",label='y=x', )
plt.errorbar(values[:,0],values[:,1], yerr=values[:,2],label="", capsize=3, fmt='.', markersize=10, ecolor="black", elinewidth=0.5, markeredgecolor="black", color="w")

plt.legend()
plt.show()

Engineeでは機械学習エンジニアを募集してるので興味のある方は是非お問い合わせください！

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up