はじめに
前回、FreeCADで作成したモデルをPrePoMaxに読み込ませて、三点曲げと四点曲げの梁について曲げ応力とたわみを計算しました。
やり方
- FreeCADで作成したモデルをSTEP形式でエクスポートします。
- そのファイルをPrePoMaxにインポートします。
- メッシュ作成、材料設定、境界条件設定をして計算します。
- 結果を表示します。
条件
- 前回と同様に、メッシュは最大サイズ5mmとして作成しました。
- 境界条件は前回と同じです。ただし、エッジに集中荷重を加える場合、PrePoMaxでは入力した荷重がエッジを構成する個々の接点に加わります。今回の三点曲げの梁ではエッジに集中荷重として125Nを加えます。エッジの接点数が9の場合は、図1に示すように125Nを9で割った13.89Nを荷重値として入力します(Z軸の逆方向に力を加えるため、「-」を付けています)。

図1 集中荷重の設定
計算結果
三点曲げと四点曲げのX方向の垂直応力の計算結果をそれぞれ図2と図3に示しました。
三点曲げは、Z変位の最小値が-1.86 mm(下方向に最大値)、X軸方向の応力の最大値が46.77MPaとなりました。材料力学による理論値は変位が1.86mm、応力値が46.87MPaですので、理論値とほぼ一致した結果が得られました。ただし、X軸方向の応力の最小値は-51.41MPaとなっており、理論値-46.87MPaに比べてやや大きい値となっています。
四点曲げは、Z変位の最小値が-2.56 mm(下方向に最大値)、X軸方向の応力の最大値が47.03MPaとなりました。材料力学による理論値は変位が2.56mm、応力が46.87MPaですので、こちらも理論値とほぼ一致した結果が得られています。ただし、X軸方向の応力の最小値は-50.18MPaとなっており、こちらも理論値-46.87MPaに比べてやや大きい値となっています。
上記において、X軸方向の垂直応力の最小値が得られた位置は荷重を加えた位置と一致していることから、このような応力値となった理由として応力集中が考えられます。図4と図5に、三点曲げと四点曲げの荷重点と2節点(1要素)離れた位置のX軸方向の垂直応力の計算結果を示します。これらの図において、荷重点から2節点(1要素)離れたオレンジ色で示す位置の応力値は理論値(理論値は図4、図5いずれも-46.87MPa)とほぼ一致していることが分かります。材料力学では応力集中は考慮していないため、図4、図5のように荷重点から少し離れた位置の応力値を理論値と比較するのがよいと考えます。
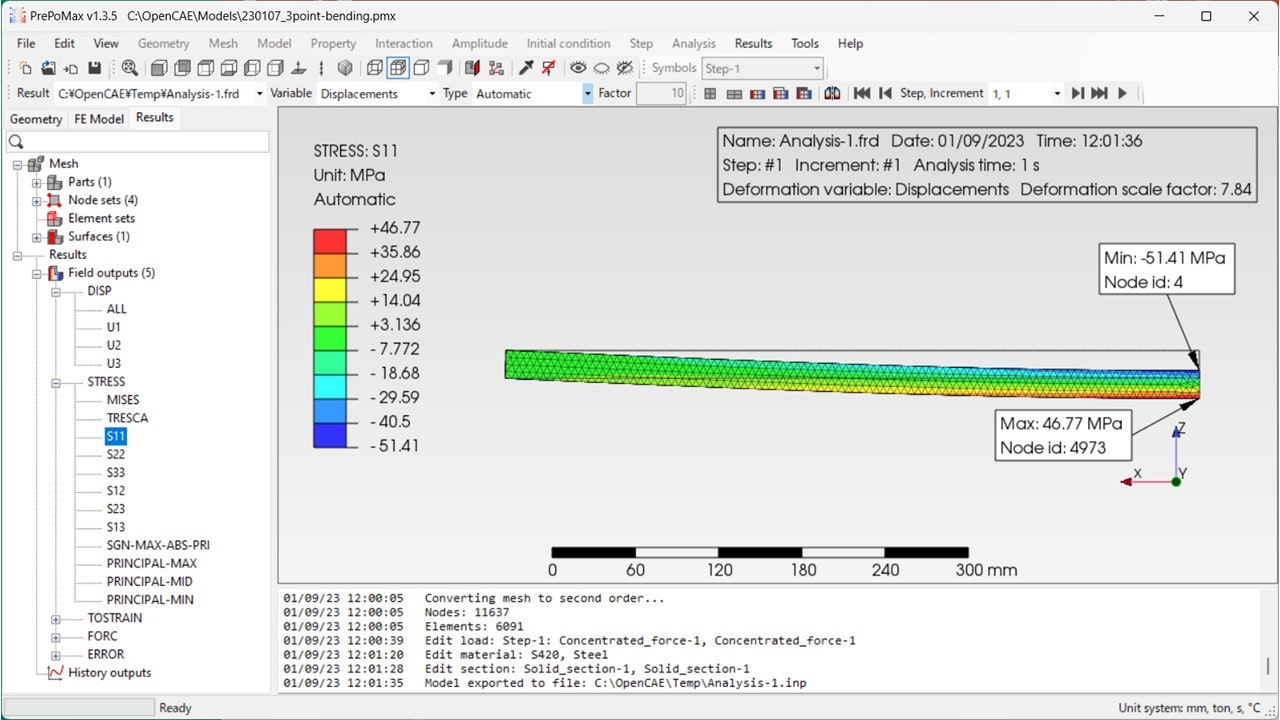
図2 三点曲げ梁の1/4モデルのX軸方向の垂直応力の計算結果

図3 四点曲げ梁の1/4モデルのX軸方向の垂直応力の計算結果
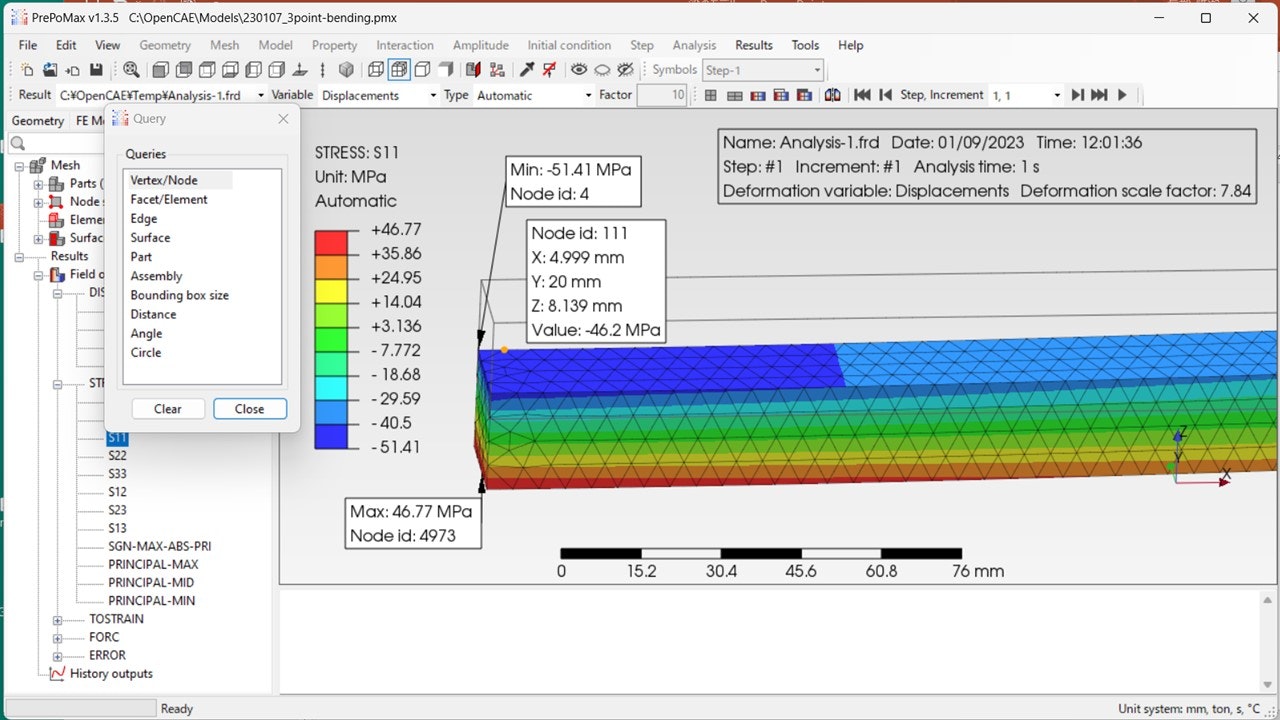
図4 三点曲げ梁の1/4モデルの荷重点付近のX軸方向の垂直応力の計算結果

図5 四点曲げ梁の1/4モデルの荷重点付近のX軸方向の垂直応力の計算結果