はじめに
遅ればせながら、最近CAEの勉強を始めました。趣味でやっているため、CADには無償のFreeCADを使っています。このFreeCADはCAEもできる優れものです。
今回は勉強がてら、矩形断面の三点曲げと四点曲げの梁について、FreeCADを使って曲げ応力とたわみを計算しました。
梁の寸法と荷重位置
図1と図2に示します。材料は鋼(ヤング率210GPa、ポアソン比0.30)とします。

図1 三点曲げ梁の寸法と荷重位置

図2 四点曲げ梁の寸法と荷重位置
FreeCADで作成した1/4モデル
計算は、幅と長さをそれぞれ半分とした1/4モデル(幅20mm、厚さ20mm、長さ500mm)により行いました。図3と図4に作成したモデルと境界条件を示します。図において、長さ方向はX方向、幅方向はY方向、厚さ方向はZ方向になります。
図4においては、モデルの上面を面分割して、分割位置で荷重を加えられるようにしています。面分割はFreeCAD 平面を複数の面に分割するを参考にして行いました。
1/4モデルのため境界条件には少し工夫が必要です。分割面に垂直方向の変位は0とし、支点での反力と釣り合う荷重を加えます。
三点曲げ、四点曲げとも、メッシュは最大サイズ5mm、細かさ中程度の条件で分割しました。

図3 三点曲げ梁の1/4モデルと境界条件

図4 四点曲げ梁の1/4モデルと境界条件
計算結果
三点曲げと四点曲げのX方向の垂直応力(sx)の計算結果をそれぞれ図5と図6に示しました。
三点曲げは、Z変位の最小値が-1.86 mm(下方向に最大値)、X軸方向の応力の最大値が46.74MPaとなりました。材料力学による理論値は変位が1.86mm、応力値が46.87MPaですので、理論値とほぼ一致した結果が得られました。ただし、X軸方向の応力の最小値は-49.84MPaとなっており、理論値-46.87MPaに比べて絶対値でやや大きい値となっています。
四点曲げは、Z変位の最小値が-2.56 mm(下方向に最大値)、X軸方向の応力の最大値が47.02MPaとなりました。材料力学による理論値は変位が2.56mm、応力が46.87MPaですので、こちらも理論値とほぼ一致した結果が得られています。ただし、X軸方向の応力の最小値は-50.04MPaとなっており、こちらも理論値-46.87MPaに比べて絶対値でやや大きい値となっています。
なお、図5と図6において、X軸方向の応力値の最小値が理論値に比べて絶対値でやや大きくなっている理由は、PrePoMaxによる三点曲げと四点曲げの梁(はり)の曲げ応力の計算で書いたように、これらの応力値は荷重点で生じているため、応力集中によるものと考えられます。

図5 三点曲げ梁の1/4モデルのX軸方向の垂直応力の計算結果
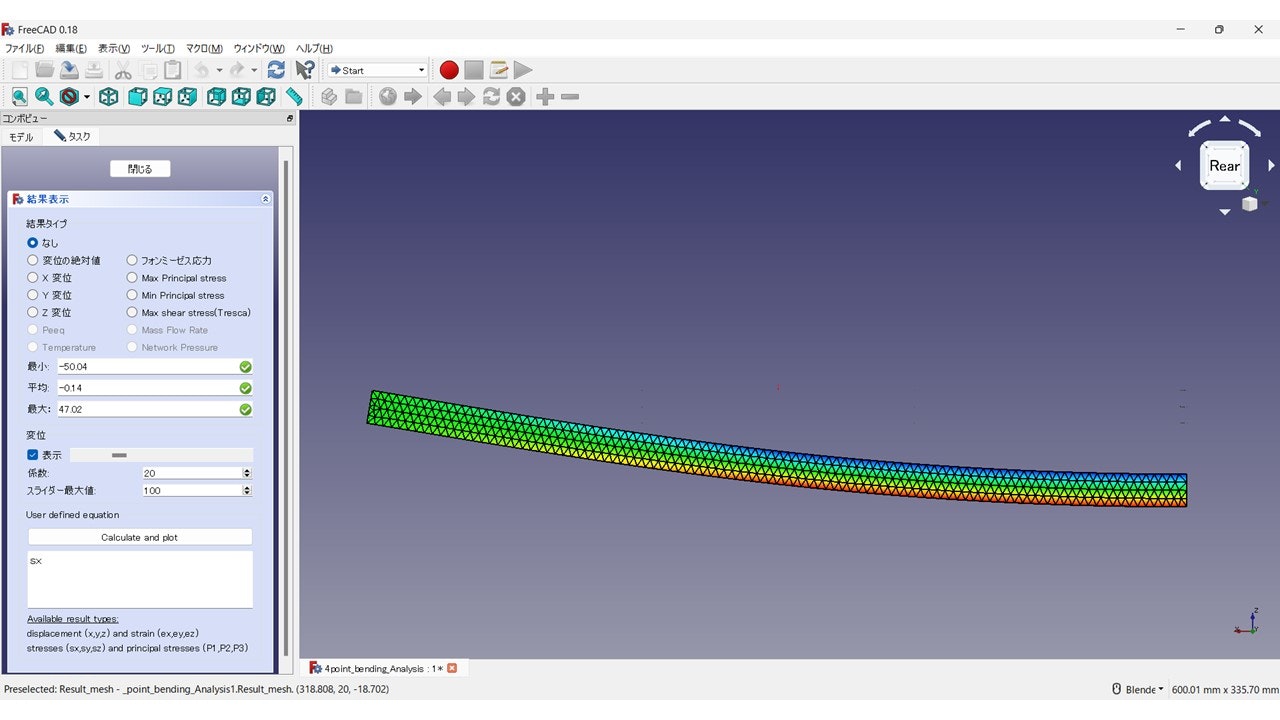
図6 四点曲げ梁の1/4モデルのX軸方向の垂直応力の計算結果
終わりに
四点曲げの荷重位置の設定に多少難儀しましたが、X軸方向の最大応力値については、理論値とほぼ一致する結果が得られました。