Pythonでお手軽・異常検知 [ホテリング理論編]

この記事は Akatsuki Advent Calendar 2017 の 5 日目の記事です。
4日目: エンジニア組織マネージメント7つの習慣

異常検知とは

いわゆる機械学習のビックテーマの一つです。異常検知は大多数のデータから正常時とは異なる振る舞いを示すデータを機械が自動的に検出する技術の事を示し、クレジットカードの不正使用検知、半導体製造プロセスの故障検知、スパムメールの判定など幅広い業界で適用されています。異常検知の基本的な流れとしては大雑把に言うと以下の通りです。

1. 正常時のデータの振る舞いのパターンを見つける
2. 上記から正常・異常の境目となる閾値を設定する
3. 観測データが閾値を超えたら異常発生と判断する

なお、ホテリング理論及び、異常検知全般の理論は以下の書籍を参考にしました。
入門 機械学習による異常検知 - Rによる実践ガイド -

この記事でやりたい事

本記事では異常検知の入門として、ホテリング理論をPythonで実装していきます。ホテリング理論は古典的な外れ値検出技術ではありますが、現代においても幅広く応用されている技術で異常検知の入門には最適です。あくまでも入門ですので、用いてるデータは1変数で、出来るだけ直感的に理解し易い題材を用います。実務に活かす為にはもっと深く学ぶ必要がある事を強調しておきます。

ホテリング理論の解説

STEP1: データのパターンを定量的に評価

データセットの平均値、分散を計算します。
異常時データが含まれていても構いませんが、極少数である事が前提です。

\widehat {\mu } = \frac{1}{N}\sum_{n=1}^{N}x^{(n)} \\
\widehat {\sigma}^{2} = \frac{1}{N}\sum_{n=1}^{N}(x^{(n)} - \widehat {\mu } )^{2} 

STEP2: 検証するデータx'の異常度合いを計算

異常度合い(以下、異常度)は検証するデータx'の平均値からのズレをまず計算します(下式の分子)。異常なデータであれば当然、平均的な値との差が大きくなりますよね。

分母に分散(=標準偏差の二乗)が来ていますが、これはデータのバラツキが大きい場合は多少の外れ値は多めに見て、データのバラツキが小さい場合はちょっとした外れ値でも異常ではないかと疑う事を意味します。

a(x') =\biggl( \frac{x' - \widehat {\mu }}{\widehat {\sigma}}\biggr)^{2}

STEP3: 異常判定の閾値を設定

ここがホテリング理論のポイント！
本理論ではデータの分布が正規分布に従っている事を仮定しており、STEP3で示した異常度の計算結果はデータ数が十分に大きければ自由度1のカイ二乗分布に従うとしています。

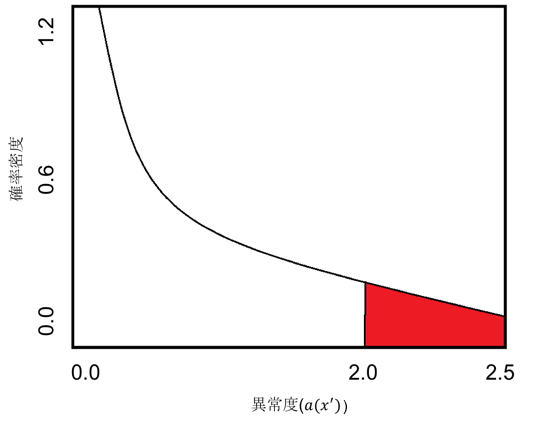
以下の図は自由度1のカイ二乗分布の曲線を示します。任意の体重データ(例:x' = 70kg)があり、STEP2で示した式を用いて異常度を計算すると結果が2.0となったとします。この2.0という異常度が正常な体重データなのか、異常な体重データなのかをどうやって判断するかが問題です。

下図に示されたカイ二乗分布の曲線は曲線で囲まれた面積が確率を表しています。すなわち面積が大きければ大きい程高い確率で発生するデータであると言え、そのデータは正常である可能性が高く、反対に面積が小さければごく稀に発生する異常時データである可能性が高いと言えるわけです。

異常度2.0が発生する確率は図中の赤い部分を見れば評価できます。逆に言えばこの面積が非常に小さい(例えば1%)時の異常度を計算しておけば、その異常度を超えたらデータは異常であると言える事になりますね。

カイ二乗分布の数式はあえて示しません。分布表を見れば数値は直ぐに分かりますし、Pythonのモジュールを使えばパパッと計算できるからです。今回は1%水準の異常度の値を閾値として使ってみます。発生確率1%の閾値を超えたデータなら異常であると判断して良いだろう、という考え方に基づいています。

用意したデータセット

今回は統計解析等によく使われるRのデータセットから「Davis」というデータを使用します。このデータセットには200人分の性別、身長(実測)、体重、身長(自己申告)の4種類のデータが用意されており、その中から体重のデータを使用する事にします。
https://vincentarelbundock.github.io/Rdatasets/datasets.html

まずはデータのヒストグラムを描画してデータの分布を見てみます。

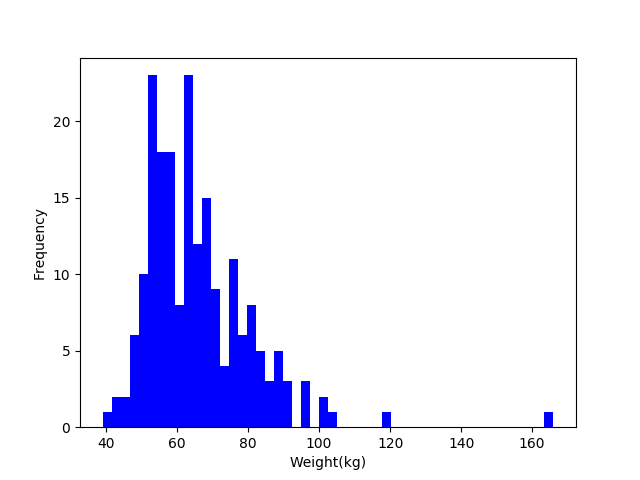
明らかに外れている値(119kg、166kg)がありますね。
これらの値を異常と判定できれば成功という事になります。

ホテリング理論の実装

上記の理論をPythonコードで走り書き。

import numpy as np
import matplotlib.pyplot as plt
import csv
from statistics import mean, variance
from scipy import stats

# データセットの読み込み
num = []
data = []
with open('Davis.csv', 'r', encoding="utf-8") as f:
    reader = csv.reader(f)
    header = next(reader)

    for row in reader:
    	num.append(int(row[0]))  #標本番号を取得
    	data.append(int(row[2])) #体重データを取得

# 標本平均
mean = mean(data)

# 標本分散
variance = variance(data)

# 異常度
anomaly_scores = []
for x in data:
	anomaly_score = (x - mean)**2 / variance
	anomaly_scores.append(anomaly_score)

# カイ二乗分布による1%水準の閾値
threshold = stats.chi2.interval(0.99, 1)[1]

# 結果の描画
plt.plot(num, anomaly_scores, "o", color = "b")
plt.plot([0,200],[threshold, threshold], 'k-', color = "r", ls = "dashed")
plt.xlabel("Sample number")
plt.ylabel("Anomaly score")
plt.ylim([0,100])
plt.show()

実行結果

上記のスクリプトを実行した結果が以下の図です。赤い点線はカイ二乗分布から出した閾値、横軸は標本番号で、1人目、2人目...と体重データを順に並べているだけです。

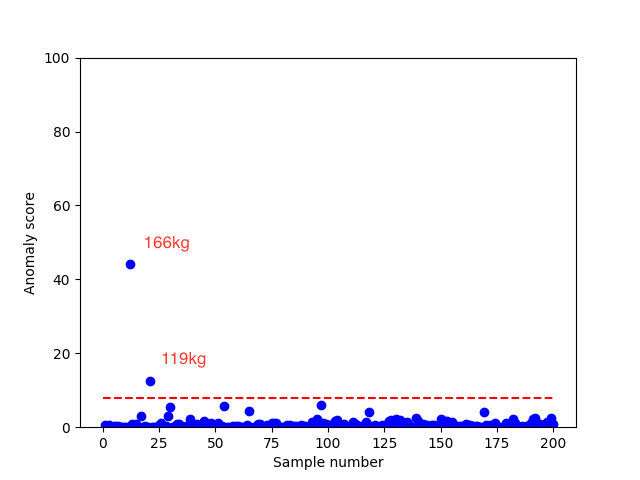
狙い通り119kg, 166kgのデータが閾値を超えており、適切に異常検知が出来ていることが分かります。ヒストグラムを見ればこの２点が異常である事は人間の目には明らかですが、ホテリング理論で異常度と閾値を設定する事で定量的にデータの正常、異常を判定する事が可能になるわけです。これで自動的に異常を検知するシステムが構築できますね。

今回試した手法の問題点

単一の正規分布を仮定している点

例えば正規分布の山が二つ出てくるような分布の場合、ホテリング理論の適用は難しいです。

異常度の計算を一つの平均値からのズレで表現している点

平均値が動的に変化するような時系列データの解析には向いていません。

閾値の設定は結局手動でやっている点

発生確率1%のラインを異常判定の閾値と設定しましたが、それは結局人間の主観なんですよね。この理論だけではシステム構築毎に人間が何%以下を異常と判断するか検討しなければなりません。(それって本当に機械学習と言えるのか？)

最後に

上述した通り色々と課題がありますが、これらの対処法は既に幅広く研究されています。異常検知技術は他にも沢山あるので、機会があれば他の手法についても記事を書いてみます(既に十分、記事化されてる感あるけど)

おまけ

記事で一部の数式を書くときに下記のサービスを使わせて頂きました。画面上で手書きした数式が自動でLaTeX形式に変換されます。
Math
https://webdemo.myscript.com/views/math.html