Pythonによるマルコフ連鎖モンテカルロ法(MCMC)

■初めに

こちらの記事ではマルコフ連鎖モンテカルロ法に関する解説をpythonのコード付きで行っております。
実装したものを用いたい場合にはnotebookを下記のGitHubレポジトリにアップしていますので、クローンを行って使用してください。
https://github.com/YusukeOhnishi/BayesianStatistics

■モンテカルロ法

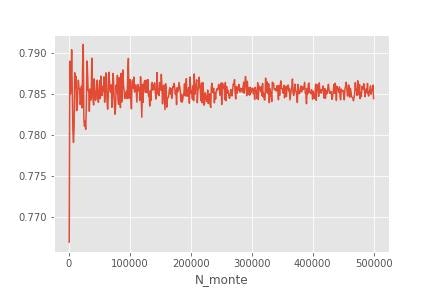
モンテカルロ法についてまずは見ていきます。これは乱数を用いた数値計算となっています。例えば、円の面積を求めるといったものが代表的な例です。また、モンテカルロ法では一般的に、ランダムに打つ点の個数を多くするほど精度が良くなっていくことが知られています。

下記の実装では円の面積を求める計算をモンテカルロ法を用いて行っています。この結果を見ると今回の場合の正解値(0.7854)に収束してい様子がわかります。

N_monte_list=np.arange(1000,500000+1,1000)

#結果を格納するリストを作成
sampling_rate_list=[]

for N_monte in N_monte_list:
    x_data=np.random.rand(N_monte)
    y_data=np.random.rand(N_monte)
    
    sampling_rate=np.sum((x_data**2+y_data**2)<1)/N_monte
    
    sampling_rate_list.append(sampling_rate)

■棄却サンプリング

上記の例では、円の面積を求めるということを行いましたが、ベイズ統計では、事後分布からモンテカルロ法にてサンプリングを行います。そのための手法として棄却サンプリングがあります。
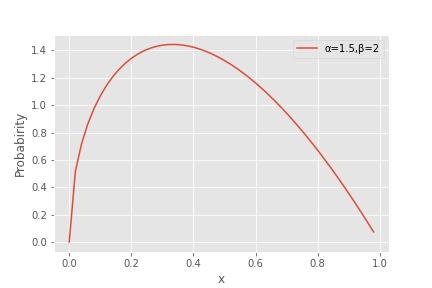
例として事後分布がbeta分布に従うとして考えていきます。Beta分布とは下記のような分布のことです。

\beta(x|\alpha,\beta)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{\int_0^1\mathrm{d}t [t^{\alpha-1}(1-t)^{\beta-1}]}

今回行うこととしてはモンテカルロ法を用いてBeta分布のサンプリングすることである。棄却分布ではBeta分布p(x)(目標分布)に従う乱数の発生は諦め、サンプルが簡単な一様分布q(x)(提案分布)を用意し、これが、下記を満たすように定数Mを調整するということを行います。

f(x)\leq Mg(x)

つまりMg(x)はf(x)を覆うような一様分布です。よってMの値はBeta分布の最大値の接するようにg(x)が与えられるように決めます。

次に棄却サンプリングのアルゴリズムについてみていきます。これは下記の5つのステップのようになります。
1.g(x)の定義域から乱数xをサンプリング
2.Mg(x)地域から乱数rをサンプリングし、これが下記を満たすかを判定

r\leq p(x)

3.真の場合はそのxのカウントを1増やし、偽の場合はそのサンプルを棄却する。
4.2と3をN回繰り返す。
5.各xでカウント数のヒストグラムを作成

このようにすることで各xに対して乱数を生成した場合にBeta分布以下の範囲内に収まる確率を得ることができ、これが事後確率に比例するということを用いています。

これをpythonにて実装していきます。まずはライブラリのインポート、グラフのスタイル設定、乱数のセード固定を行います。

#ライブラリインポート
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta,uniform
from scipy import optimize

#グラフの見た目変更
plt.style.use("ggplot")

#乱数のSeedを固定
np.random.seed(999)

次にベータ分布の最大値を取る点の探索を行います。ここで最小化問題に帰着させるために、最小化を行うメソッド(fmin)にBeta分布に-1を掛けたものを渡しています。

#Beta分布のパラメータ設定
a,b=1.5,2
#x軸を作成
x=np.linspace(beta.ppf(0.001,a,b),beta.ppf(0.999,a,b),1000)
#Beta関数の密度関数を定義
p=beta(a,b).pdf
#最大化された結果(x座標)を取得
res=optimize.fmin(lambda x:-p(x),0.3)
#最大化された結果(y座標)を取得
y_max=p(res)

これで最大値(今回の場合1.443)が求まったので、これでMg(x)までが求まったことになります。よって、この値を用いて、棄却サンプリングを行います。まずはサンプリングを行います。

#サンプリング数
NMSC=50000
#x軸方向のサンプリング（0～1の区間でサンプリング）
x_mcs=uniform.rvs(size=NMCS)
#y軸方向のサンプリング（0～y_maxの区間でサンプリング）
r=uniform.rvs(size=NMSC)*y_max

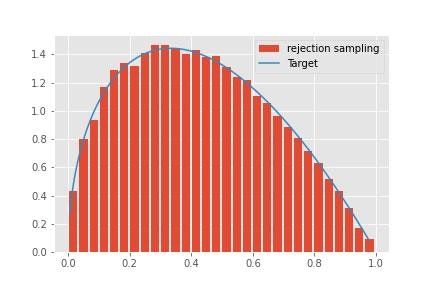
次にこれらを用いて、棄却するかの判定を行います。これを実行し結果を表示すると下記のようになります。

#Beta分布以下かどうかの条件判定
accept=x_mcs[r<=p(x_mcs)]

#結果の表示
plt.hist(accept,density=True,bins=30,rwidth=0.8,label='rejection sampling')
plt.plot(x,beta.pdf(x,a,b),label='Target')
plt.legend()
plt.show()

この結果、事後分布のサンプリングを行うことができました。

■次元の呪い

前節では1次元のBeta分布を事後分布として、この分布からサンプリングを行いました。しかし、これが2次元、3次元と増えていったときに対応できないという問題があります。

なぜなら今回の場合は1次元に対して50000点のサンプリングを行っていましたが、これは2次元空間上だとある一つの線分上のみで議論を行っていることと同じになります。そのため、同じ密度で点を打とうとすると、50000×50000の点が必要になります。
より一般には1次元空間上でのN点サンプルリングを行いたい場合、同程度の精度をm次元空間上で出す場合にはNのm乗の点が必要になります。

これは数値計算を行う上で単純に考えると、一次元空間での点の数を2倍に計算時間が2倍になる場合、2次元では4倍、3次元では8倍の計算時間になります。よって次元数のに増加によって、計算時間が現実的ではない時間になってしまい、対応できないということになります。
このような事象を次元の呪いといいます。

■マルコフ連鎖モンテカルロ法

上記のような次元の呪いは点をランダムに取ってきた場合に、起こる事象でした。そのため、何かしらの工夫が必要になるということがわかりますが、この工夫の1つがマルコフ連鎖モンテカルロ法(MCMC)となります。

それではMCMCについて見ていきます。MCMCは端的に表現すると、前回の試行の結果を用いて、次の試行を確率的に改善していく手法になります。MCMCの大雑把な流れは下記のような5段階構成になります。
1.初期値$\theta$を適当に決める。
2.乱数で今の$\theta$から新しい$\theta_{\mathrm{new}}$を探す。（マルコフ連鎖）
3.次の条件式を判定する。

p(\theta_{\mathrm{new}}|D)>p(\theta|D)

4.真の場合は状態を更新。偽の場合はある程度の確率で受容。
5.2~4を繰り返す。

この2番目のマルコフ連鎖を用いるという点が通常のモンテカルロ法との違いになります。

そこで、このマルコフ連鎖について見ていきます。
$\theta$を確率変数として、$\theta_1\rightarrow\theta_2\rightarrow\cdots\rightarrow\theta_{t}$のように時間変化とともに状態が変わっていく時系列を考えます。この状態の変化の推移のことを確率過程と呼びます。
このとき、$n$番目の状態$\theta_n$が$n-1$番目の状態$\theta_{n-1}$のみによって決定する場合、これをマルコフ性を持つといいます。またこのマルコフ性を持つ確率過程のことをマルコフ連鎖といいます。数式で書くと下記のようにまります。

p(\theta_n|\theta_{n-1},\cdots,\theta_2,\theta_1)=p(\theta_n|\theta_{n-1})

例として天気の移り変わりを考えます。天気としては晴れ、曇り、雨の
3つの種類があるとし、今日の天気によって翌日の天気が何になるのかの確率が決まるとします。それぞれの確率は下記のように設定しておきます。

今日の天気	明日晴れの確率	明日曇りの確率	明日雨の確率
晴れ	0.6	0.3	0.1
曇り	0.5	0.4	0.1
雨	0.4	0.3	0.3

これは行列の形に書くことができ、下記のようになります。

P_{\mathrm{trans}}=
\begin{bmatrix}
0.6 & 0.3 & 0.1 \\
0.5 & 0.4 & 0.1 \\
0.4 & 0.3 & 0.3
\end{bmatrix}

この$P_{\mathrm{trans}}$を遷移核といいます。このとき十分月日がが経った後にどの天気になっている可能性が高いのかということを見ていきます。

まずはライブラリのインポート、図のスタイル設定、乱数シードの固定を行います。

#ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

#グラフの見た目変更
plt.style.use("ggplot")

#乱数のSeedを固定
np.random.seed(999)

次に遷移核と各種パラメータを定義します。遷移核には上記と同じものを入力します。

#遷移核を定義 0:晴れ、1:曇り、2:雨
p_trans=np.zeros([3,3])
p_trans[0,0]=0.6
p_trans[0,1]=0.3
p_trans[0,2]=0.1
p_trans[1,0]=0.5
p_trans[1,1]=0.4
p_trans[1,2]=0.1
p_trans[2,0]=0.4
p_trans[2,1]=0.3
p_trans[2,2]=0.3

#モンテカルロステップ数
NMCS=100

#現在の天気(初期状態では晴れとする)
c_state=0

このc_stateを更新することで、状態を変化させていきます。またその状態の変化の過程を記録しておき、最後にそれぞれの天気がどのくらいの確率で現れたのかを見ます。

#遷移過程を保存しておくリスト
c_arr=[c_state]

#遷移を行う
for i in range(NMCS):
    current=np.random.choice(3,1,p=p_trans[c_state,:])
    c_state=current[0]
    c_arr.append(c_state)
    
print('晴れの確率：',c_arr.count(0)/len(c_arr))
print('曇りの確率：',c_arr.count(1)/len(c_arr))
print('雨の確率：',c_arr.count(2)/len(c_arr))

晴れの確率： 0.46534653465346537
曇りの確率： 0.36633663366336633
雨の確率： 0.16831683168316833

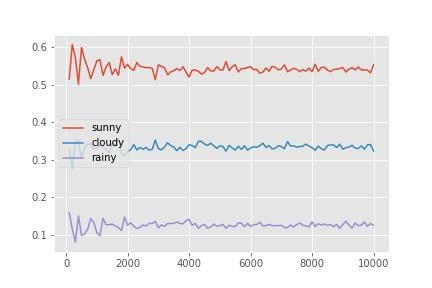
この結果がモンテカルロステップ数が100の場合の結果なので、モンテカルロ数を変化させた場合に確率がどのように変化していくのかを確認すると下記のような結果が得られます。

この結果を見ると、それぞれの確率はある一定値に収束していることがわかります。この収束状態のことを定常分布といいます。
この定常分布に収束するかどうかは遷移核がある特定の条件を満たすかどうかで決まります。

■詳細つり合い

上記の定常分布へ収束する場合の条件についてみていきます。これは確率の流れを考えることで求まります。確率の流れは、ある2つの状態$\theta,\theta'$を考えたとき$p_{\mathrm{trans}}(\theta|\theta')$を遷移核(移りやすさ)、$p(\theta)$を事後確率(起こりやすさ)として、これらの積$p_{\mathrm{trans}}(\theta|\theta')p(\theta)$で与えられます。この場合は状態$\theta$から$\theta'$への確率の流れとなります。もし、この流れとその反対、すなわち状態$\theta'$から$\theta$への確率流れが等しいとき、確率の流れは相殺されるため、分布はある一定状態に落ち着くだろうということが想像できます。つまり定常状態に収束するということです。式で書くと下記のようになります。

p_{\mathrm{trans}}(\theta|\theta')p(\theta)=p_{\mathrm{trans}}(\theta'|\theta)p(\theta')

これを詳細つり合いといいます。またこれはMaster方程式という確率分布の変化に対する方程式の時間変化項になっています。Master方程式については説明を割愛しますが興味のある方は下記等を参照ください。

https://www.sciencetime.jp/note/102
https://note.com/1380649/n/n559a43c9e01b
https://balance-tutorial-ja.readthedocs.io/ja/pngmath/appendices/master_equation.html

この詳細つり合いを満たす遷移核に関していくつか種類がありますが、この記事では下記の3つに関して見ていきます。

・メトロポリス・ヘイスティングス(M-H)法
・Gibbsサンプラー
・ハミルトニアンモンテカルロ

用語の説明になりますが、上記の方法を用いると定常分布に収束しますが、MCMCではすぐには定常分布にならないこともあります。MCMCの定常分布に収束するまでの期間をバーンイン、またはウォームアップと呼びます。

▶メトロポリス・ヘイスティングス(M-H)法

詳細つり合いを満たせば定常状態に落ち着くので、これを満たすような遷移核を見つけたいがこれは容易ではないです。また、遷移核に従う乱数を発生させることも容易ではありません。そのため、M-H法ではサンプリングが簡単な遷移核$q(\theta|\theta')$(提案分布)で代用するということを行います。そして、適当に置いた遷移核では詳細つり合いを満たさない場合があるため、これを満たすように補正を行います。

具体的には下記のようなことを考えます。
適当な遷移核$q(\theta|\theta')$を用意し、このとき確率の流れを考えると下記のようになります。

q(\theta|\theta')p(\theta')\neq q(\theta'|\theta)p(\theta)

そのため下記のような補正係数rを考えます。

r=\frac{q(\theta|\theta')p(\theta')}{q(\theta'|\theta)p(\theta)}

この係数rを導入することで詳細つり合いが成り立つことになります。

rq(\theta'|\theta)p(\theta)= q(\theta|\theta')p(\theta')

これを用いることでM-H法を扱うことができます。そのアルゴリズムとしては下記のようになります。

1.初期値$\theta$を適当に決める。
2.遷移核$q(\theta'|\theta)$から乱数を生成し、新しい$\theta'$を取得する。
3.下記の条件式を判定する。

q(\theta'|\theta)p(\theta)>q(\theta|\theta')p(\theta')

4.真の場合は補正係数rを用いて補正する。偽の場合は$\theta'$を受け入れる。
5.2~4を繰り返す。

仮置きの遷移核としてはランダムウォークがよく用いられます。これはどの方向に行く確率も同じとしたものになります。そのため、下記が成り立ち、$r$は事後分布の比で与えられます。

q(\theta|\theta')=q(\theta'|\theta)

r=\frac{p(\theta')}{p(\theta)}

これをpythonにて実装していきます。
まずはライブラリのインポート、図のスタイル設定、乱数シードの固定を行います。

#ライブラリのインポート
import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as plt
%matplotlib inline

#グラフの見た目変更
plt.style.use("ggplot")

#乱数のSeedを固定
np.random.seed(999)

次に今回はBeta分布に適用するとして、Beta分布の初期値等、及び$x$座標を定義します。

#Beta分布のパラメータ指定
a,b=1.5,2

#x座標定義
x=np.linspace(beta.ppf(0.001,a,b),beta.ppf(0.999,a,b),100)

次は各種パラメータを定義します。

#初期値
theta=0.8

#モンテカルロステップ数
NMCS=20000

#ランダムウォークの1ステップでの動く幅
epsilon=0.5

ここまでできれば準備は完了したので結果を格納するリストを定義し、モンテカルロ計算を行っていきます。

#モンテカルロステップごとのthetaの値を入れるリスト
theta_mcs=[theta]

#モンテカルロ計算
for i in range(NMCS):
    theta_new=theta+epsilon*np.random.randn()
    if beta.pdf(theta_new,a,b)>beta.pdf(theta,a,b):
        theta=theta_new
    else:
        r=beta.pdf(theta_new,a,b)/beta.pdf(theta,a,b)
        if np.random.rand() < r:
            theta=theta_new
    theta_mcs.append(theta)

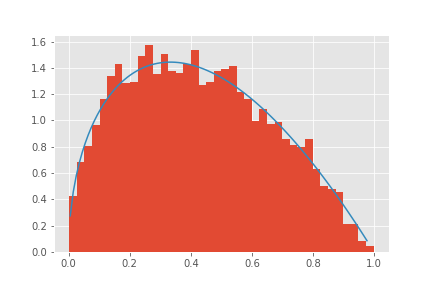
これを実行し、結果を表示しますが、この際に上記で述べたバーンインがあるため、最初のいくつかを取り除く必要があります。今回の場合は1000個を取り除き表示を行います。この結果Beta分布のサンプリングが綺麗に行えていることがわかります。

#バーンインの期間を除いておく
plt.hist(theta_mcs[1000:],density=True,bins=40)
plt.plot(x,beta.pdf(x,a,b))
plt.savefig('./figure/fig_Metropolis-Hastings')
plt.show()

最後に

この記事では概念を理解するということに主眼をおいていたため、実装を比較的標準的なライブラリのみを用いて行いました。しかしpython にはもっと簡単に実装できる方法としてpystanというライブラリを用いた方法もあります。そのため、実際に用いる場合にはこのライブラリを用いて実装を行うことをお勧めします。