Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@Yushin-Tati

Python初心者の備忘録 #19 ~機械学習入門編05~

Last updated at Posted at 2024-12-18

はじめに

今回私は最近はやりのchatGPTに興味を持ち、深層学習について学んでみたいと思い立ちました！
深層学習といえばPythonということなので、最終的にはPythonを使って深層学習ができるとこまでコツコツと学習していくことにしました。
ただ、勉強するだけではなく少しでもアウトプットをしようということで、備忘録として学習した内容をまとめていこうと思います。
この記事が少しでも誰かの糧になることを願っております！
※投稿主の環境はWindowsなのでMacの方は多少違う部分が出てくると思いますが、ご了承ください。
最初の記事：Python初心者の備忘録 #01
前の記事：Python初心者の備忘録 #18 ~機械学習入門編04~
次の記事：まだ

今回は分類器の精度指標についてまとめております。

■学習に使用している資料

Udemy：【後編】米国データサイエンティストがやさしく教える機械学習超入門【Pythonで実践】

■分類器の精度指標

前回記事で取り扱った回帰ではMSE、RMSE、MAE、$R^2$といった精度指標をあげていたが、分類となるとその数はより多くなる。
(例：Log Loss、TP・TN・FP・FN、混同行列(Confusion Matrix)、Acuracy、Precision...)

★様々な精度指標の中から最適なものを選択しなければならない

▶TP、TN、FP、FN

  • 正解ラベルに対して正解/不正解かを表す指標
  • ほとんどすべての分類の精度指標の基礎となる

TP：True Positive(真陽性)
TN：True Negative(真陰性)
FP：Flase Positive(偽陽性)
FN：False Negative(偽陰性)
※陽/陰は正解ラベルを表しており、真/偽は正解ラベルに対して予測が正しかったかを表す。
image.png

▶混同行列(Confusion Matrix)

  • データセットで各クラスがいくつ正解/不正解しているかを表す行列(表)で、一目でモデルの分類傾向がわかる

image.png

Python

  • sklearn.metrics.confusion_matrixをimportする
    - confusion_matrix(y_true, y_pred)で結果を返す
    ※上図で言うと正解がy_true、予測がy_predに当たる
  • 戻り値はNumPy Array

★混同行列をきれいに表示する

  • sklearn.metrics.ConfusionMatrixDisplayをimport
  1. ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=model.classes_)でインスタンス生成
    ※cmにはconfusion_matrix()の戻り値を指定する
  2. .plot()で描画
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

# データロード
df = sns.load_dataset('iris')
y_col = 'species'
X = df.drop(columns=[y_col])
y = df[y_col]
# hold-out
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

# モデル学習
model = LogisticRegression(penalty='none')
model.fit(X_train, y_train)

# 予測
y_pred = model.predict(X_test)

# 混同行列
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
cm = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=model.classes_)
disp.plot()

image.png

▶Accuracy(正解率)

  • 全てのデータの中でいくつ正解しているかを表す指標で、多クラスにもそのまま使用可能
    $Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$

Accuracyはクラスのデータ数に偏りがある場合はうまく活用できない
例：全て0と予測する使い物にならないモデルでも高いAccuracyになってしまう
image.png

Python

# import
from sklearn.metrics import accuracy_score

# サンプルデータ
y_true = [1, 1, 0, 1, 0, 0, 1, 1]
y_pred = [1, 1, 1, 0, 0, 1, 0, 1]

# Accuracy算出
accuracy_score(y_true, y_pred)  # -> 0.5

▶Precision(適合率)

  • 陽性と分類した中で実際に陽性だった割合で、PPV(Positive Predictive Value)ともいわれる
    $Precision=\frac{TP}{TP+FP}$
  • Accuracyと違い、陽性が極端に少ない場合の偏りのケースでも適切に評価可能
  • しかし、陰性が少ないケースには対応できない

image.png
image.png

例：医者の見落としをキャッチするAI
image.png

なぜPrecisionが高い必要があるのか
AIモデルが陽性と判断した場合は必ず陽性であるようにしたいから
本当は陰性なのに陽性と判断するようなPrecisionが低いモデルだと、再読影に戻ってくるデータが膨大になる！

★AIモデルのユースケースによって、高くすべき精度指標が変わってくる！！

Python

# ライブラリのimport
from sklearn.metrics import precision_score

# Precision計算(y_tureとy_predはAccuracyと同じ)
precision_score(y_true, y_pred)  # -> 0.6

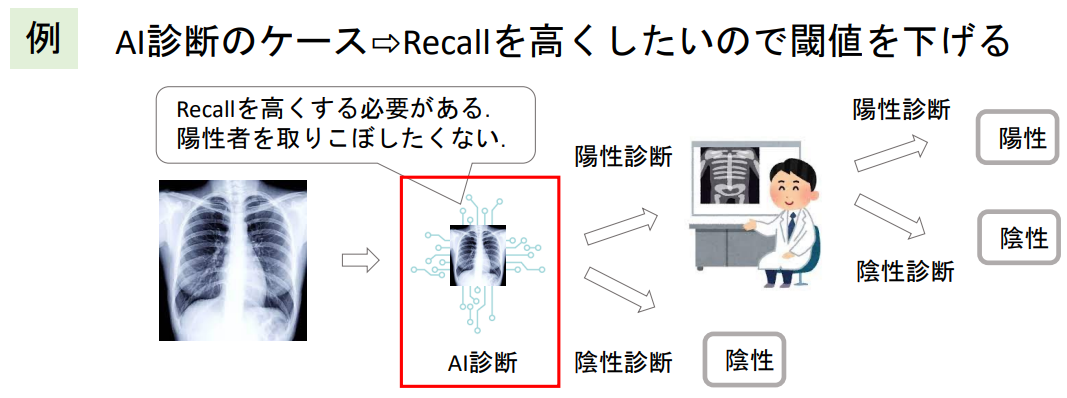
▶Recall(再現率)

  • 陽性のデータに対してどれだけ陽性と予測できたかを表す指標で、医療系の分野ではSensitivity(感度)と呼ばれることもある
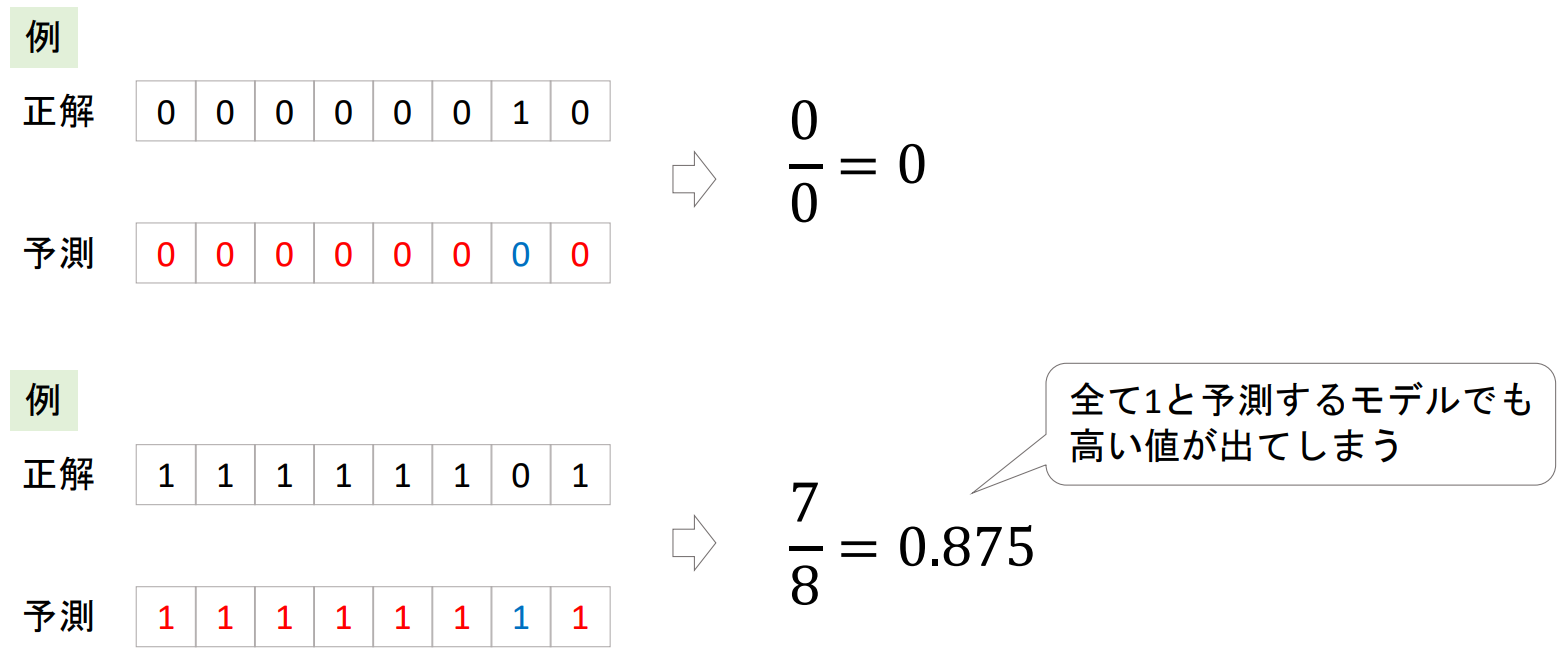
    $Recall=\frac{TP}{TP+FN}$

image.png

  • 陽性が極端に少ないケースでも適切に評価できる場合がある
  • ただ、すべて要請に分類するようなモデルでは100%の精度が出てしまうので注意

image.png
★陽性を取りこぼしたくないモデルなどに使用することが多い

例：人間の判断を行う前処理として、明らかに陰性のものは排除する
image.png

Python

# ライブラリのimport
from sklearn.metrics import recall_score

# Recallの算出
recall_score(y_true, y_pred)  # -> 0.6

▶Specificity(特異度)

  • 陰性のデータに対してどれだけ陰性と予測できたかを表す指標
    $Specificith=\frac{TN}{TN+FP}$

image.png

  • sklearnに実装されていないので、recall_score()を使用する

Python

import numpy as np

# 下記で1はFlase、0はTrueとなり、Pythonでは1はTrue、0はFlaseと扱ってくれるので、逆転させることができる
np.array(y_true)!=1

# Specificityの算出
recall_score(np.array(y_true)!=1, np.array(y_pred)!=1)  # -> 0.33333333333

▶多クラス分類における評価指標

  • 多クラスの場合は大きく2つの計算方法がある
    - macro平均：クラスレベルで平均を取る
    - micro平均：データレベルで平均を取る

例：A、B、Cという３つのクラスのAccuracyを計算する場合
・macro平均はクラスごとにAccuracyを計算して、その平均を取る。
・micro平均はクラスを区別せず、データ全体でAccuracyを計算する。
image.png

  • Accuracyは通常micro平均を取る
  • そのほかPrecision、Recall、Specificityは通常macro平均を取る
    ※Precision、Recall、Specificityのmicro平均はAccuracyと同じになる

Python

※今回はPrecisionを例にとる

  • precision_srore(y_true, y_pred, average)のaverage引数にmacro、microを渡すことで、算出可能
    → 他のrecall_score, accuracy_score, etc.も同様
  • Noneを渡すとクラス別に指標をlistで返してくれる
# データロード
df = sns.load_dataset('iris')
y_col = 'species'
X = df.drop(columns=[y_col])
y = df[y_col]

# hold-out
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

# モデル学習
model = LogisticRegression(penalty='none')
model.fit(X_train, y_train)

# 予測
y_pred = model.predict(X_test)

# average=None (= precision_score(y_test, y_pred, average=None).mean())
print(precision_score(y_test, y_pred, average=None)) # -> [1.         0.94444444 0.90909091]

# average=macro
print(precision_score(y_test, y_pred, average='macro')) # -> 0.9511784511784511

# average=micro
print(precision_score(y_test, y_pred, average='micro')) # -> 0.9555555555555556

# same as accuracy
print(accuracy_score(y_test, y_pred)) # -> 0.9555555555555556

▶分類の閾値による精度のコントロール

  • 分類器は通常、確率の閾値によって分類ラベルを決定する
  • 閾値の調整によりそれぞれの精度指標をコントロールすることができる
    例：陽性の確率40％の時【閾値が50％→陰性】、【閾値が30％→陽性】
    ※閾値は必ずしも50％である必要はない、アプリケーションによって適宜選択する。

スクリーンショット 2024-11-26 212840.png
※陽性を取りこぼしたくないので...

▶PrecisionとRecallのトレードオフ

  • PrecisionとRecallはトレードオフの関係にある
    Precision：TP/TP+FP(陽性と分類したうち本当に陽性だった割合)
    Recall：TP/TP+FN(全陽性中、陽性と分類できた割合)

なぜトレードオフの関係にあるのか
Recallの値をあげるということは「FPを下げる」、つまり陽性と判断する閾値を低く設定する必要がある。
しかしそうすると本当は陰性なのに陽性と分類される確率が上がり「FNが上がる」ので、Precisionの値が低くなる。
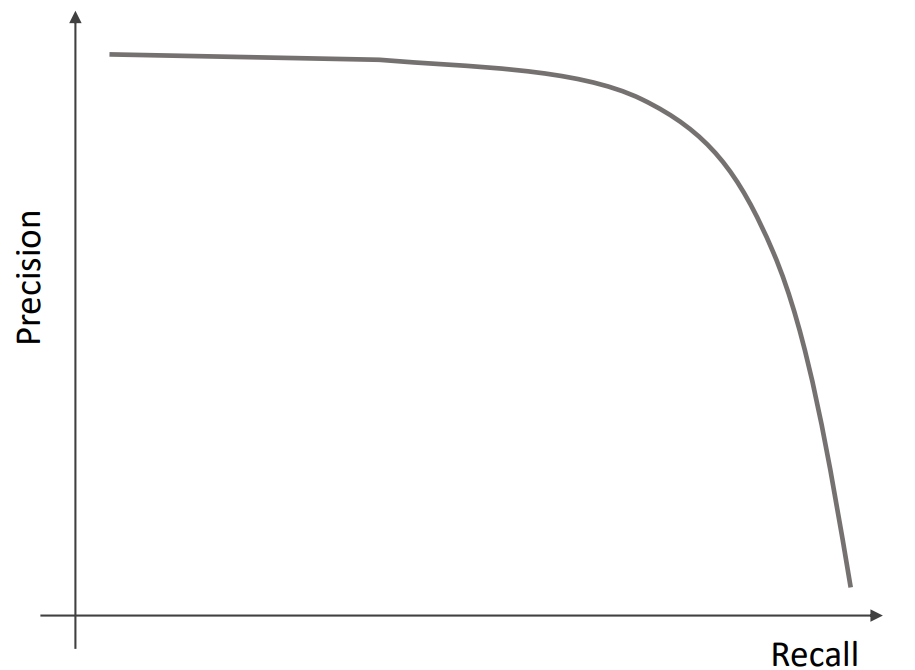
image.png

Precision-Recall Curve

  • 閾値に対するPrecisionとRecallの推移を表す図で、適切な閾値を決定するのに使用される
  • 特にこだわりがなければF値を使用する

image.png

Python

  • sklearn.metrics.precision_recall_curveライブラリを使用することで、一発でcurveを描くためのデータを求めることが可能
    - precision_recall_curve(y_true, probas_pred)でprecision、recall、thresholds(閾値)の1次元NumpyArrayを返す
    → prabas_prod：各データの確率値(陽性の確率)のリスト
    ※precisionとrecallの最後の値は1と0であり、それに対応するthresholdsは存在しないことに注意

次のPythonコードでは外部ファイルを使用しているので、実際に手を動かしながら参照したい方は下記からDLしてください。
https://github.com/Yushin-Tati/Learning_machine_learning
・heart_preprocessed.csv

# import 
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.metrics import precision_recall_curve

# データの用意
df = pd.read_csv('heart_preprocessed.csv')
y_col = 'target'
X = df.drop(columns=[y_col])
y = df[y_col]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

#　モデル構築
model = LogisticRegression(solver='liblinear')
model.fit(X_train, y_train)
# .predict()は閾値が50%
y_pred_proba = model.predict_proba(X_test)

# Curve用データ算出（陽性の確率が欲しいので、y_pred_proba[:, 1]としている）
precision, recall, thresholds = precision_recall_curve(y_test, y_pred_proba[:, 1])

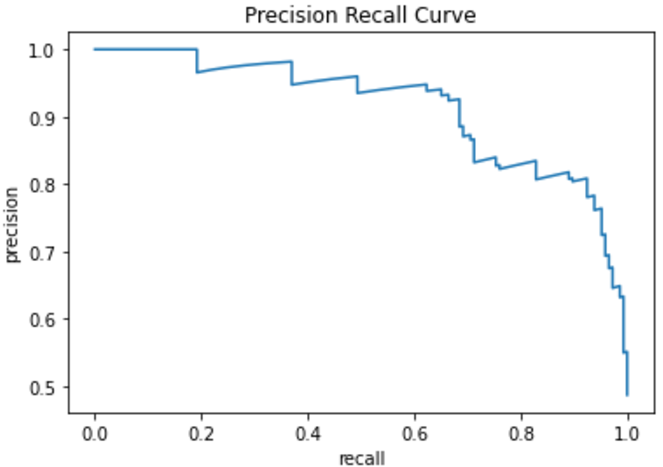
# 描画
plt.plot(recall, precision)
plt.xlabel('recall')
plt.ylabel('precision')
plt.title('Precision Recall Curve')
plt.show()

image.png

▶F値(F-score、F1-score)

  • PrecisionとRecallの調和平均を取った値で、どちらも犠牲にしたいくない場合はF値が高くなるようにモデルを構築する

$Fscore=\frac{2×Recall×Precision}{Recall+Precision}$

Python

  • sklearn.metrics.f1_scoreライブラリをimportする
  1. f1_score(y_true, y_pred)で算出可能
  2. 他の指標同様にaverage引数に'macro'や'micro'などを選択することで多クラス分類用のF1scoreを計算することができる
# import
from sklearn.metrics import f1_score, recall_score, precision_score

# sample data
y_true = [1, 0, 0, 1, 0, 0, 1, 1]
y_pred = [1, 1, 1, 0, 0, 1, 0, 1]

# F1
print(f1_score(y_true, y_pred)) # -> 0.4444444444444445

# 調和平均ver
from scipy.stats import hmean
hmean([recall_score(y_true, y_pred), precision_score(y_true, y_pred)]) # -> 0.444444444444444

# recall
print(recall_score(y_true, y_pred)) # -> 0.5

# precision
print(precision_score(y_true, y_pred)) # -> 0.4

RecallとPrecisionのF値の推移グラフを描画

ThresholdのおけるそれぞれのRecall、Precision、F値をグラフに描画する。

# それぞれのprecisionとrecallにおけるF値(調和平均)を計算
f1_scores = [hmean([p, r]) for p, r in zip(precision, recall)]

# ThresholdはRecall,Precisionの最後の値に該当する値はないので、[:-1]でSlicingする
# 描画
plt.plot(thresholds, f1_scores[:-1], label='f1 score')
plt.plot(thresholds, precision[:-1], label='precision')
plt.plot(thresholds, recall[:-1], label='recall')
plt.xlabel('threshlold')
plt.legend()

# np.argmax()でリスト内の最大値のindexを求める
print(f'{np.argmax(f1_scores)}th threshold(={thresholds[np.argmax(f1_scores)]:.2f}) is the highest f1 score = {np.max(f1_scores):.2f}')

image.png

▶ROC(Receiver Operating Charactaristic)

  • Recall(Sensitivity)とSpecificity(TPR：True Positive Rate)はトレードオフの関係にある
  • 横軸を1－Specificity、縦軸をRecallとしたときの閾値の変化を描くカーブをROCという
    →1－Specificity(FPR：Flase Positive Rate)は陰性データに対して間違えて陽性に分類した割合を表している
  • 分類器の評価で最もよく使用される指標の一つ

$Recall(Sensitivity)=\frac{TP}{TP+FN}⇔Specificity=\frac{TN}{TN+FP}$
※陽性を優先する：高Recall、陰性を優先する：高Specificity
ROC_curve.png

Python

  • sklearn.metrics.roc_curveライブラリをimportする
  • roc_curve(y_true, y_score)でfpr、tpr、thresholdsの3つを返す
    ※y_scoreには陽性の確率の値を指定する
# import
from sklearn.metrics import roc_curve

# ROC Curveに使用する値を算出
# y_pred_probaは1つ目は陰性の確率、2つ目は陽性の確率なので[:, 1]でslicingする
fpr, tpr, thresholds = roc_curve(y_test, y_pred_proba[:, 1])

# 描画
plt.plot(fpr, tpr)
plt.xlabel('1-specificity(FPR)')
plt.ylabel('sensitivity(TPR)')
plt.title('ROC Curve')
plt.show()

image.png

▶AUC(Area Under the Curve)

  • ROCにおける制度を数値化したもので、ROCの面積に当たる
  • 1が最大で、ランダムな分類器では0.5になる

AUC_graph.png

Python

# import
from sklearn.metrics import auc
from sklearn.metrics import roc_curve

# AUC算出
fpr, tpr, thresholds = roc_curve(y_test, y_pred_proba[:, 1])
auc(fpr, tpr)  # -> 0.919542785981142

一般的にAUCが0.8を超えてくるとかなり精度の高い分類器と判断できる。
今回であれば0.9を超えているので、過学習を疑うレベルになってくる。

▶多クラス分類におけるROC

  • 多クラス分類の場合、macro平均かmicro平均を行う
    - macro平均：OvRでクラス数分のROCを描画し、その平均を取る
    - micro平均：OvRとしたときの結果(FPR、TPR)でまとめてROCを描く

image.png
multiple_ROC.png

macro平均

  • クラスレベルの平均(クラス毎の値の平均を取る)
    ※データ数の少ないクラスの値も重視
    image.png

micro平均

  • データレベルの平均(データ全体で計算する)
    ※データ数の多いクラスの結果を重視
    image.png

Python

  • 多クラスROCでは、正解ラベルはone-hotの形にする
  • macro平均を求めるにはそれぞれのクラス別のfpr、tprを求め、線形補完した後に平均を取る
  • micro平均はone-hotの形の正解ラベルと予測した確率リストを一次元配列にしてroc_curve()に入れれば良い
# データロード
df = sns.load_dataset('iris')
y_col = 'species'
X = df.drop(columns=[y_col])
y = df[y_col]

# hold-out
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

# モデル学習
model = LogisticRegression()
model.fit(X_train, y_train)

# 予測
y_pred_proba = model.predict_proba(X_test)
macro平均
# クラスをone-hotに変換
from sklearn.preprocessing import label_binarize
y_test_one_hot = label_binarize(y_test, classes=model.classes_)

# for文でそれぞれのクラスについてROCを計算
n_classes = len(model.classes_)
fpr = {}
tpr = {}
roc_auc = {}
for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_test_one_hot[:, i], y_pred_proba[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])

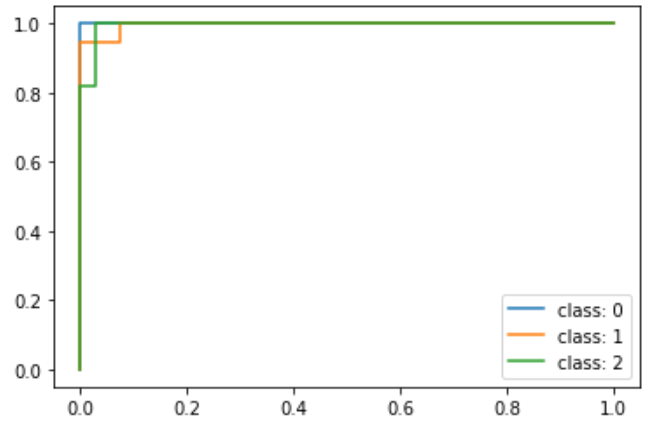
# それぞれのクラスのROCを描画
for i in range(n_classes):
    plt.plot(fpr[i], tpr[i], label=f'class: {i}')
    plt.legend()

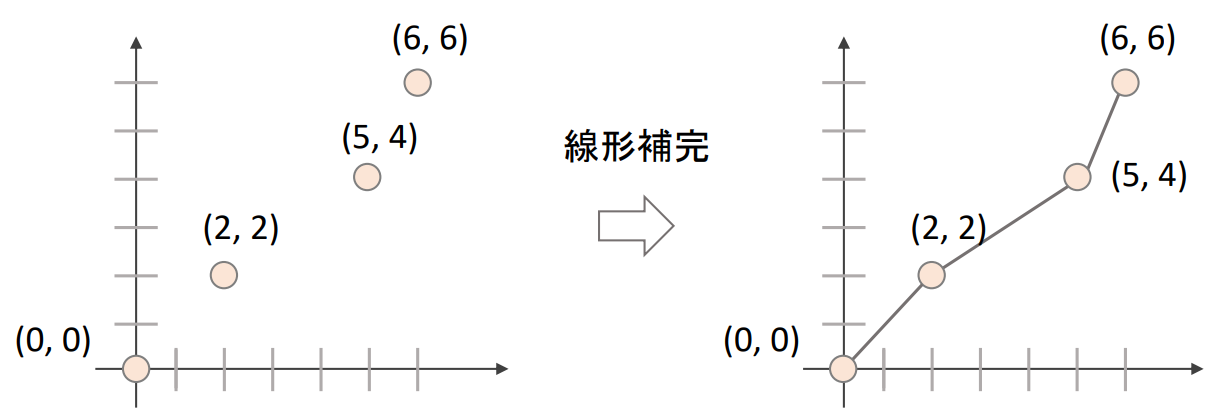
image.png

次に平均を取るのだが、下記左図で値が変わっている部分でうまく平均を取ればいいと考えられる。

しかし、下記右図のようにclass2では値が変わっているがclass0とclass1は値が変わっていないので、tprが存在せず計算できないという問題が上がる。
image.png

そこで必要になるのが線形補完である。

線形補完

  • np.iterp(x, xp, yp)で線形補完を行うことができる
    - x：補完後のx軸の値
    - xp：xの値のリスト
    - yp：yの値のリスト

image.png

線形補完の例
all_x = np.arange(7)
data_x = [0, 2, 5, 6]
data_y = [0, 2, 4, 6]
np.interp(all_x, data_x, data_y)  # -> array([0., 1., 2., 2.66666667, 3.33333333, 4., 6.])
macro平均に線形補完を適用
# 必要なxの値のリスト
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))

# 線形補完
mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):
    mean_tpr += np.interp(all_fpr, fpr[i], tpr[i])

# 全体の平均を計算
mean_tpr = mean_tpr / n_classes
fpr['macro'] = all_fpr
tpr['macro'] = mean_tpr
roc_auc['macro'] = auc(fpr['macro'], tpr['macro'])

# それぞれのクラスとmacro平均のROC
for i in range(n_classes):
    plt.plot(fpr[i], tpr[i], label=f'class: {i}')
plt.plot(fpr['macro'], tpr['macro'], label='macro')
plt.legend()

image.png

micro平均
# .ravel()で多次元を一次元に変換
fpr['micro'], tpr['micro'], _ = roc_curve(y_test_one_hot.ravel(), y_pred_proba.ravel())
roc_auc['micro'] = auc(fpr['micro'], tpr['micro'])

# それぞれのクラスとmacro平均とmicro平均のROC
for i in range(n_classes):
    plt.plot(fpr[i], tpr[i], label=f'class: {i}')
plt.plot(fpr['macro'], tpr['macro'], label='macro')
plt.plot(fpr['micro'], tpr['micro'], label='micro')
plt.legend()

image.png

次の記事

まだ

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?