はじめに
今回私は最近はやりのchatGPTに興味を持ち、深層学習について学んでみたいと思い立ちました!
深層学習といえばPythonということなので、最終的にはPythonを使って深層学習ができるとこまでコツコツと学習していくことにしました。
ただ、勉強するだけではなく少しでもアウトプットをしようということで、備忘録として学習した内容をまとめていこうと思います。
この記事が少しでも誰かの糧になることを願っております!
※投稿主の環境はWindowsなのでMacの方は多少違う部分が出てくると思いますが、ご了承ください。
最初の記事:Python初心者の備忘録 #01
前の記事:Python初心者の備忘録 #19 ~機械学習入門編05~
次の記事:Python初心者の備忘録 #21 ~機械学習入門編07~
今回はPCA(主成分分析) についてまとめております。
■学習に使用している資料
Udemy:【後編】米国データサイエンティストがやさしく教える機械学習超入門【Pythonで実践】
■主成分分析(PCA:Principal Component Analysis)
▶PCAとは
- 次元(特徴量)削減の手法の一つで、主に処理の高速化とデータの可視化のために使用される
- L1ノルムの正則化項であるLassoでは特徴量を選択的に落としていたが、PCAは特徴量を落とさずに次元を圧縮することができる
- なので、すべての特徴量が必要となる
※つまりPCAはLassoのような特徴量を選択する扱い方は難しい
▶主成分(principal component)とは
- データを最もよく表している軸のことで、他にも「分散が最大、デートとの距離が最短、射影後の分散が最大」などとも言い換えることができる
- 多次元のデータを圧縮するには第1主成分、第2主成分...のように主成分を抽出する
※第n主成分は第n-1主成分と直行する軸の中で分散が最大になる軸
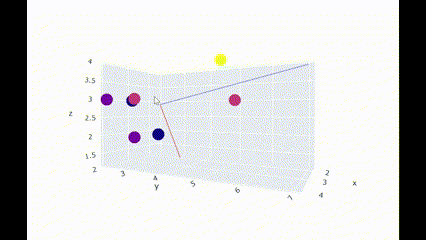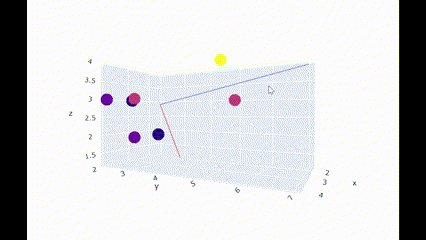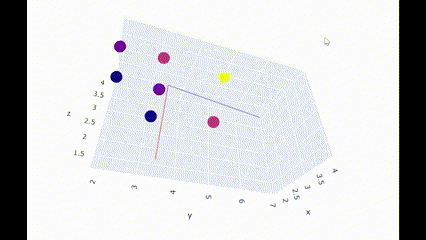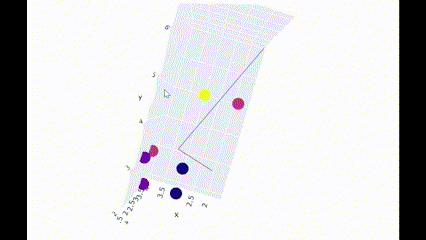
想像がつきにくいという方はJupyterLabに下記コードを入れることで、直感的に三次元プロットを操作できます。
import numpy as np
import pandas as pd
import plotly.express as px
from sklearn.decomposition import PCA
# サンプルデータ
x = np.array([3, 4, 2, 3, 4, 4, 3])
y = np.array([2, 3, 5, 5, 3, 2, 3])
z = np.array([3, 3, 3, 4, 2, 3, 2])
X = pd.DataFrame({'x': x, 'y': y, 'z': z})
pca = PCA(n_components=2)
pca.fit(X)
X_pc = pca.transform(X)
X['color'] = X['x'] + X['y'] + X['z']
# 主成分の座標作成
pc_v = []
coef = 3
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * np.sqrt(length) * coef
pc_v.append(v)
pc_df = pd.DataFrame((np.array(pc_v) + pca.mean_), columns=['x', 'y', 'z'])
pc_df['component'] =['first', 'second']
pc_mean_df = pd.DataFrame(np.array([pca.mean_, pca.mean_]), columns=['x', 'y', 'z'])
pc_mean_df['component'] = ['first', 'second']
pc_df_all = pd.concat([pc_mean_df, pc_df])
# 描画
fig = px.scatter_3d(X, x="x", y="y", z="z", color='color')
fig.add_trace(px.line_3d(pc_df_all, x='x', y='y', z='z', color='component').data[0])
fig.add_trace(px.line_3d(pc_df_all, x='x', y='y', z='z', color='component').data[1])
fig.show()
以降の説明は線形代数や数学的な内容が絡んでくるので、余裕があれば先にある程度知識を入れておいてください。それ以外の人でも概要の把握は可能となっていると思います。
▶PCAをスクラッチで実装
PCAの手順
- 標準化する
- 分散共分散行列を求める
- 固有ベクトルと固有値を求める(大きい順に第一主成分、第二主成分...と並べる)
- データを変換する
実装例
X(特徴量)と主成分の数(圧縮後の次元数)を引数にしてPCA後のXを返す関数を作成
- 平均0、標準偏差1に標準化
- Xの分散共分散行列を計算
- 固有ベクトルと固有値を求める
- 主成分にXを変換
import pandas as pd
import numpy as np
# サンプルデータ準備
x = np.array([3, 4, 2, 3, 4, 4, 3])
y = np.array([2, 3, 5, 5, 3, 2, 3])
X = pd.DataFrame({'x': x, 'y': y})
# 関数作成
def my_pca(X, num_components):
# step1. 標準化
X_meaned = X - np.mean(X, axis=0)
X_scaled = X_meaned / np.std(X_meaned, axis=0)
# step2. 分散共分散行列
cov_mat = np.cov(X_scaled, rowvar=False)
# step3-1. 固有ベクトルと固有値
eigen_values, eigen_vectors = np.linalg.eigh(cov_mat)
# step3-2. 大きい順にソート
sorted_index = np.argsort(eigen_values)[::-1]
sorted_evalues = eigen_values[sorted_index]
sorted_evectors = eigen_vectors[:, sorted_index]
subset_evectors = sorted_evectors[:, :num_components]
# step4. 変換
X_reduced = np.dot(X_scaled, subset_evectors)
return X_reduced
my_pca(X, 1)
array([[-0.49467432],
[-0.89576549],
[ 2.34350404],
[ 1.33314107],
[-0.89576549],
[-1.50503729],
[ 0.11459748]])
▶sklearnでPCA
-
sklearn.decomposition.PCAライブラリを使用
1.PCA(n_components)でインスタンス生成(n_components:使用する主成分の数)
2..fit(X)でXの主成分を計算
3..transform(X)でXを主成分の座標系に変換 - 事前に標準化する必要があることに注意
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
scaler = StandardScaler()
pca = PCA(n_components=1)
X = scaler.fit_transform(X)
pca.fit_transform(X)
array([[-0.49467432],
[-0.89576549],
[ 2.34350404],
[ 1.33314107],
[-0.89576549],
[-1.50503729],
[ 0.11459748]])
irisデータをPCAで描画
# データ準備
import seaborn as sns
import numpy as np
df = sns.load_dataset('iris')
y_col = 'species'
X = df.loc[:, df.columns!=y_col]
y = df[y_col].values
# 標準化
X_scaled = StandardScaler().fit_transform(X)
# PCA
X_pc = PCA(n_components=2).fit_transform(X_scaled)
#描画
y = y.reshape(-1, 1)
df_pc = pd.DataFrame(np.concatenate([X_pc, y], axis=1), columns=['first component', 'second component', 'species'])
sns.scatterplot(x='first component', y='second component', hue='species', data=df_pc)
▶寄与率と累積寄与率
- 寄与率:PCAを行った際に各主成分がどれほどデータを説明しているか表す指標
→ 全固有値の合計に対しての各主成分の固有値の割合
例:主成分が3つあるものをPCAで主成分を2つに圧縮した時、元からどれだけ情報が失われているのかを確認できる - 累積寄与率:寄与率を第一主成分から累積したもの
→ 特定の寄与率に達するまでに主成分がいくつ必要かを見るのに使用する
例:95%のデータを説明するためにはいくつの主成分が必要なのか...
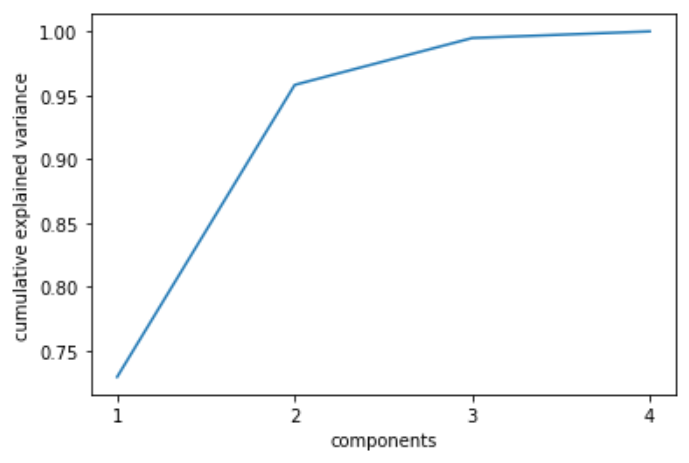
▶累積寄与率の描画
- 寄与率
→sklearn.decomposition.PCAライブラリの.explained_variance_ratio_属性で寄与率を取得
# PCA(主成分4つ)
n_components=4
pca = PCA(n_components=n_components)
pca.fit(X_scaled)
# 寄与率(第一主成分だけで約73%説明できることがわかる)
pca.explained_variance_ratio_ # -> array([0.72962445, 0.22850762, 0.03668922, 0.00517871])
# 各主成分(元の特徴量空間の座標系)
pca.components_
array([[ 0.52106591, -0.26934744, 0.5804131 , 0.56485654],
[ 0.37741762, 0.92329566, 0.02449161, 0.06694199],
[-0.71956635, 0.24438178, 0.14212637, 0.63427274],
[-0.26128628, 0.12350962, 0.80144925, -0.52359713]])
# 描画
import matplotlib.pyplot as plt
plt.plot(range(1, n_components+1), np.cumsum(pca.explained_variance_ratio_))
plt.xticks(range(1, n_components+1))
plt.xlabel('components')
plt.ylabel('cumulative explained variance')
plt.show()
▶PCAで分類器学習
- データセット:MNISTデータセット(学習:テスト=7:3)
-sklearn.datasets.fetch_openml('mnist_784')で使用可能 - MNISTデータの画像再構成(元は各ピクセル値のデータフレームなので)
下記のように28×28で表してみる

- 累積寄与率が95%になるようにPCAを行い、主成分を特徴量にろぎスティック回帰で分類器を構築する
- PCAなしとありで時間差を計測する
# データ準備
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784')
# 画像再構成
import matplotlib.pyplot as plt
im = mnist.data.iloc[0].values.reshape(28, 28)
plt.imshow(im, 'gray')
# hold-out
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(mnist.data, mnist.target, test_size=0.3, random_state=0)
# 標準化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler().fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
# PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=0.95) # 累積寄与率95%になるように自動で主成分を取ってくれる
pca.fit(X_train)
# 学習
X_train_pc = pca.transform(X_train)
X_test_pc = pca.transform(X_test)
# 圧縮の詳細(784 -> 323)
print(f"{X_train.shape[-1]} dimensions is reduced to {X_train_pc.shape[-1]} dimensions by PCA") # -> 784 dimensions is reduced to 323 dimension by PCA
# ロジスティック回帰(PCAあり)
from sklearn.linear_model import LogisticRegression
import time
model_pca = LogisticRegression()
before = time.time()
model_pca.fit(X_train_pc, y_train)
after = time.time()
print(f"fit took {after-before:.2f}s") # -> fit took 357.10s
# Accuracyを算出
from sklearn.metrics import accuracy_score
y_pred_pc = model_pca.predict(X_test_pc)
accuracy_score(y_test, y_pred_pc) # -> 0.9195238095238095
# 画像再構成
import matplotlib.pyplot as plt
index = 2
im = X_test[index].reshape(28, 28)
plt.imshow(im, 'gray')
# ロジスティック回帰 (PCAなし)
model = LogisticRegression()
before = time.time()
model.fit(X_train, y_train)
after = time.time()
print(f"fit took {after-before:.2f}s") # -> fit took 854.03s(PCAありに比べて2倍ほど時間がかかっている)
# Accuracyを算出
y_pred = model.predict(X_test)
accuracy_score(y_test, y_pred) # -> 0.910047619047619
▶PCAの注意点
- 基本的にな目的は可視化と高速化
※PCAをしても必要な特徴量は減らない(データ取得のコストは下がらない) - 過学習を避けることで(=精度の向上)が目的であれば、Lassoなどの特徴量を選択するアルゴリズムのほうが一概に良い
- 次元が削減されても解釈性は向上しない