UnityのShader(ShaderLab/HLSL)入門その1 : Shaderの書き方

Shaderについて

Shaderは3Dの物体を画面上に表示するときに、画面上のピクセルに対してどのような色を表示するかを決めるプログラムである。
このプログラムによって、物体の色と3D空間上の光源や影の影響などを計算し、物体の見え方を決めることができる。
リアルに似せた自然なものや、イラストチックなもの、光の影響が小さく古いCGのような見え方のものなど、様々な表現ができる。
UnityやBlenderなど多くの3DCGソフトではMaterialというものを指定することで物体の見え方を決めるが、そのときMaterialに対応したShaderが存在し、Shaderのプログラムがはたらいている。
Shaderによって、表現できるものは何も物体の陰影だけではなく、物体の表面に図形や模様を描くこともできる。
更には、3Dソフトで使用する物体とは別に、無限に広がる空間上に立体的な図形を描き、表示することもできる。
ShaderToyは、Shaderのプログラムを投稿するサイトであり、ShaderToyによって用意されたテクスチャとShaderのみによって描かれた作品を見ることができる。
ShaderToy

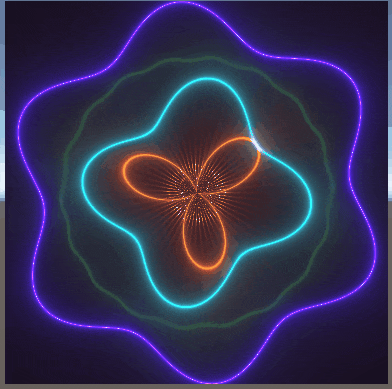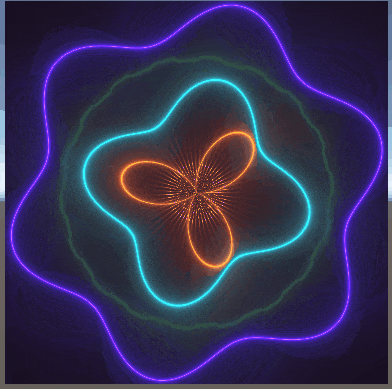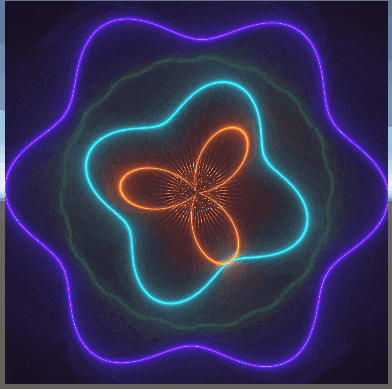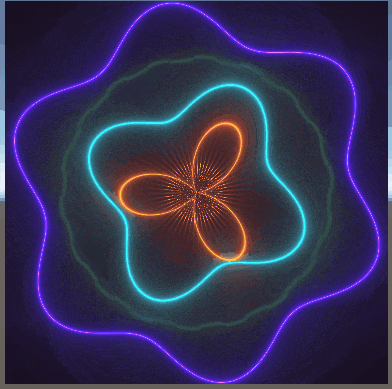
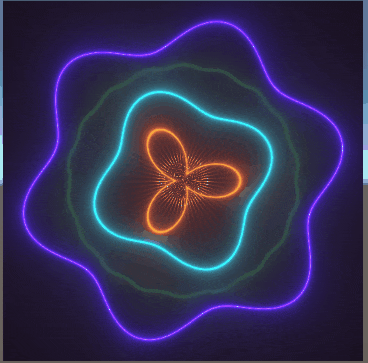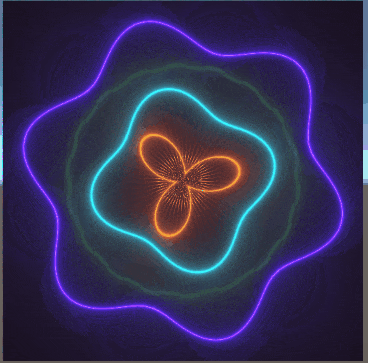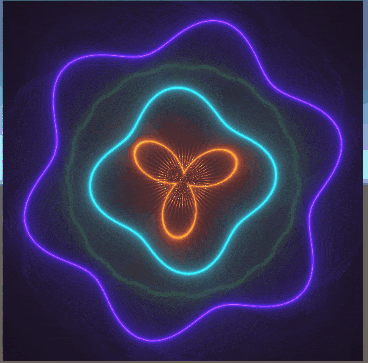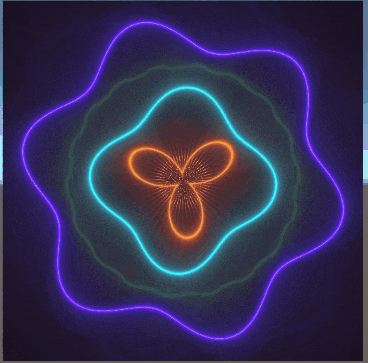
以下に、数枚載せている画像は、過去に私がシェーダーを書いてできたものである。

pic.twitter.com/QYm1czFVWk

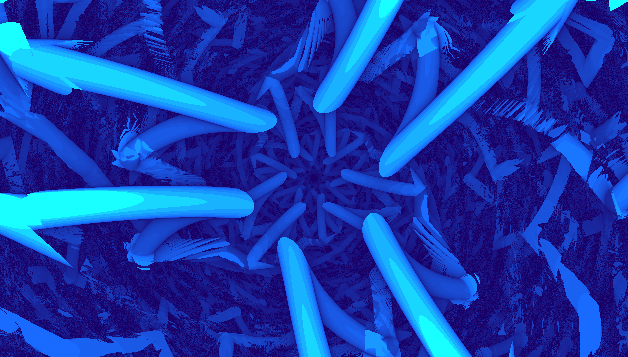
— ユムル (@Yumuru_n) August 23, 2022

GPUパーティクルとレイマーチングの併用は意外といけるのかもしれない pic.twitter.com/XQ4kROUYOq

— ユムル (@Yumuru_n) May 12, 2022

201219_Raymarch - ShaderToy

私が、UnityのShader言語であるShaderLab/HLSLを学ぼうとしたとき、初心者がとっつきやすく、分かりやすく書いた記事が見当たらず、とても苦労をした。
そのため、この記事では私が2年近くこの言語を触ってきた知識をまとめる。
C++の入門であるような、using namespace std; を「おまじない」と言って説明を省くというようなことはせず、細かく解説する。情報が足りないと後々困るんだもん
なので、最初は流して読んでしまっても構わない。また、時々リンクも貼るが、そちらも、軽く目を通すくらいで良い。

ちなみに、最近はShader Graphが出てきて、そちらの方が熱いのではないかとも思うが、
まあ、Shader GraphでもHLSLを用いてプログラムを書くことができ、細かい複雑なプログラムはノードベースのみで描くよりも、HLSLも使用した方が書きやすいと思われる。また、Shader GraphはUnityの昔ながらのBuildinのRender Pipelineでは使用できない。
加えて、Shader GraphはHLSL言語を使える人であれば、すぐに使いこなすことができるようになるものである。
したがって、この記事ではShader Graphについては述べず、ShaderLab/HLSLの話をする。

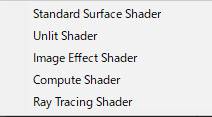
Unity(Buildin Render Pipeline)のShaderの種類

まず、UnityのShaderは、次のものがある。

この中で、Image Effect Shader と Ray Tracing Shader については自分は全くよくわからないので、説明を省く。

Standard Surface Shaderと、Unlit Shaderは画面を描画するときに、その色などの表示を決める処理を書く。
Compute ShaderはGPUのパワーを計算に使うためのもの。

Standard Surface Shader

通称はSurface Shader
Unityの標準のマテリアルに設定されている、Standard シェーダーのような基本的なライティングの処理を、簡単な設定項目を指定するだけでやってくれる。
実際に書き込むのは次に示すように、マテリアルの表面の色とかメタル/非メタルとか滑らかさとかそういう項目。

struct SurfaceOutputStandard
{
    fixed3 Albedo;      // ベース (ディフューズかスペキュラー) カラー
    fixed3 Normal;      // 書き込まれる場合は、接線空間法線
    half3 Emission;
    half Metallic;      // 0=非メタル, 1=メタル
    half Smoothness;    // 0=粗い, 1=滑らか
    half Occlusion;     // オクルージョン (デフォルト 1)
    fixed Alpha;        // 透明度のアルファ
};
struct SurfaceOutputStandardSpecular
{
    fixed3 Albedo;      // ディフューズ色
    fixed3 Specular;    // スペキュラー色
    fixed3 Normal;      // 書き込まれる場合は、接線空間法線
    half3 Emission;
    half Smoothness;    // 0=粗い, 1=滑らか
    half Occlusion;     // オクルージョン (デフォルト 1)
    fixed Alpha;        // 透明度のアルファ
};

引用元 : サーフェスシェーダーの記述, https://docs.unity3d.com/ja/current/Manual/SL-SurfaceShaders.html
参考 : サーフェスシェーダーの例, https://docs.unity3d.com/ja/current/Manual/SL-SurfaceShaderExamples.html

Unlit Shader

Surface Shaderのように、ライティングの処理はやってくれないが、シンプルで自由に書くことができる
3Dモデルから与えられた情報から画面上の色を決める処理を書く。

Compute Shader

上記2つのShaderは、画面の描画時の処理を書き込むものであったが、
Compute ShaderはC#から動かし、並列的にGPUのパワーで演算をさせるシェーダーである。
Unityの普段の画面の描画とは関係がない。

これらの3つのShaderはどれも、書き方を覚えてしまえばテンプレートを使わずに、空のファイルから簡単に書くことができる。

この記事では、基本的にUnlit Shaderを用いて説明する。Surface Shaderの書き方については丁度いい頃合いで説明する。
Compute Shaderは、HLSLに慣れて他の人の記事を読めばできるので説明は省く。

画面の描画を記述をするShaderの処理の流れ

詳細は参考のリンク先の最初の画像や、Googleで画像検索をして出てくる画像などを見てほしいところであるが、自分はとりあえずShaderを書くときに困らないだけの基本的な部分を説明する。

参考 : Shader Labについての個人的なまとめ, https://note.com/yoda0280/n/ne709228eb51e
参考 : "Unity Shader 処理の流れ" でGoogle画像検索

1. Rendererによる描画

Unityでモデルを表示するとき、Mesh RendererなどにMaterialを設定して表示する。
このとき、RendererはMaterialに紐づけられたShaderを用いて描画を行う。
また、
MaterialはShaderのプログラムに与えるプロパティの値を設定するもの。
モデルは多角形(ポリゴン)を複数組み合わせることでできる形についての情報(メッシュ)を含む。基本的にはこの多角形は三角形。

2. 頂点シェーダー

メッシュの頂点ごとに実行される。
メッシュの頂点情報を入力に、頂点シェーダーによって後の処理に繋ぐ情報の変換がされる。
具体的には、

• メッシュの頂点座標を変換する。
  メッシュの頂点の座標をObject空間 -> World空間 -> View空間 -> Screen空間まで変換する。
  Object空間 : メッシュ自体の座標
  World空間 : Sceneのワールド座標
  View空間 : カメラを原点におく座標
  Screen空間 : カメラの視野角や有効な距離の範囲などの情報を適用した座標
  普通、この変換のための関数(UnityObjectToClipPos関数)を使用するので難しいことは考えなくていい。
• テクスチャ画像の参照する位置に対応する座標を指定する。
  メッシュのデータをそのまま使う場合は基本的にいじらないでそのままにする。
• その他法線ベクトルや頂点カラーなどの情報を受け渡す。(必要なら)
• 頂点シェーダーにより、モデルの形状を変形させることもよくある。

3.フラグメントシェーダー (別名:ピクセルシェーダー)

画面上のピクセルごとに実行される。つまりフルHD (1920x1080)で画面いっぱいに描画するなら1フレームに2,073,600個分だけ実行される。
頂点シェーダーによって変換されたデータをもとに、主に画面上の色を決定するシェーダー。
一番よくいじるシェーダー。

UnityのShaderの書き方

Shaderの言語について

Shaderの言語を3つ紹介する。

• Cg
  NVIDIAが開発した言語。2012年に開発が停止されていて、Unityも昔はこの言語を使っていたが、今は使われていない。
• HLSL
  Microsoftが開発した言語。現在のUnityが使用する言語。
• GLSL
  OpenGLとかWebGLとかで、広く一般に使われる言語。
  HLSLとのシェーダの書き方にはさほど大きな違いは無いので、シェーダーについて調べるときにはGLSLも検索ワードにして調べるといい。
  例えば、次のページはとても参考になる。
  GLSL contents - wgld.org

一番簡単なShader

まず、一番シンプルに単色を描画するシェーダーから、UnityのShaderLab/HLSLの構文や処理の流れなどを説明する。

まずファイルの拡張子は.shaderである。

Shaderファイルを作成する。

今回は説明のため、中身をまるっと書き換えてしまっている。
ただ白を表示するだけの、省略できるところは省略した一番簡単なシェーダーを書いた。

Shader "Custom/VerySmallShader"
{
  SubShader
  {
    Pass
    {
      CGPROGRAM
      #pragma vertex vert
      #pragma fragment frag

      #include "UnityCG.cginc"

      float4 vert(float4 vertex : POSITION) : SV_POSITION
      {
        return UnityObjectToClipPos(vertex);
      }

      float4 frag(float4 vertex : SV_POSITION) : SV_TARGET
      {
        return 1;
      }
      ENDCG
    }
  }
}

その後、Shaderファイルを右クリックして、マテリアルを作成し、適当に出したCubeに適用してみた。

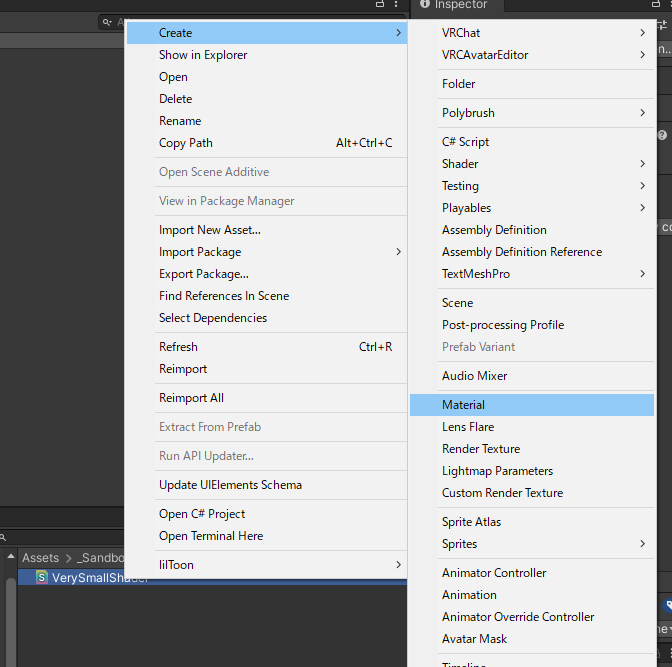
画像のように、真っ白に表示された。

Shader {}

一番外側に書く。Shaderの名前を決める。
この名前は、Materialの設定画面の上部の、Shaderを選択する部分の表示に関わる。

SubShader {}

Shader {} の内側に書く。
複数記述できる。その場合、SubShader内で使用するShaderの機能によって、実行環境によって使用されるSubShaderが異なることがある。
その実行環境が、一番上のSubShaderを使用できない場合は、一つ下のものを使用しようとする。それもできない場合は、更に一つ下のものを使用しようとする。

Pass {}

SubShader {}の内側に書く。
シェーダーの役割によって複数記述することがある。

CGPROGRAM ~ ENDCG

この中にプログラムを書いていく。
CGと書いてあるが、HLSL言語で書いていく。
この外は全部ShaderLab。

pragma

コンパイラに情報を伝える。ここでは、頂点シェーダーとフラグメントシェーダの関数名を指定している。

pragma vertex vert : 頂点シェーダーの関数名がvertであることを指定。
pragma fragment frag : フラグメントシェーダーの関数名がfragであることを指定。

ここの設定を変えれば、頂点シェーダーやフラグメントシェーダの関数名を変えることができる。
(例 : 頂点シェーダーをVS, フラグメントシェーダをFS)
pragmaで関数名を指定したものは、記述するプログラム内から呼び出すことはないが、指定した役割のために実行される。
記述するプログラムの中に他の関数を書くことができるが、それらはプログラム内で呼び出さなければ実行されない。

include

外部のファイルをここに展開している。UnityCG.cgincはUnityエンジン内のファイルを参照している。
その他のファイルを参照するときは、Shaderのファイルからの相対パスか、AssetsもしくはPackagesからの絶対パスによって参照する。

今回の場合では、vert関数内のUnityObjectToClipPos関数の定義がUnityCG.cgincに書かれている。

参照するファイルの中身をそのままこの場所に展開する。
そして、呼び出す関数はそれより前に書かなければいけないので、vert関数の後にこのincludeを書くとコンパイルエラー。

関数定義 vert, frag

頂点シェーダー、フラグメントシェーダを定義している。
C言語にとても近い構文であるが、見慣れない部分がある。
float4などのHLSL独自の型。
コロン(:)とそのあとにPOSITIONなどの、セマンティクスと呼ばれるキーワード。
これらについて説明する。

HLSLの型

まず、floatをベースとしたベクトル型や行列型がある。
float : 普通のfloat
float2 : 2次元ベクトル (2つのfloat)
float3 : 3次元ベクトル (3つのfloat)
float4 : 4次元ベクトル (4つのfloat)
float2x2 : 2x2行列 (2x2のfloat)
float3x3 : 3x3行列 (3x3のfloat)
float4x4 : 4x4行列 (4x4のfloat)

そして、これらのint, boolバージョンがある(int2, bool2など)。
また、16bitの小数点型でhalfとそのベクトル、行列がある。

ベクトル型について、その中の値のアクセスは3通りある。

float v0, v1, v2, v3;
float4 f4 = float4(0.2, 0.5, -0.8, 1.0); // 例として4次元のfloatベクトル型
// x, y, z, wによるアクセス
v0 = f4.x;
v1 = f4.y;
v2 = f4.z;
v3 = f4.w;
// r, g, b, aによるアクセス
v0 = f4.r;
v1 = f4.g;
v2 = f4.b;
v3 = f4.a;
// 添え字によるアクセス
v0 = f4[0];
v1 = f4[1];
v2 = f4[2];
v3 = f4[3];

また、上の書き方で逆に値を代入することもできる。

f4.x = 0.6;
f4.b = 1.2;
f4[3] = -3.2;

ベクトル型の値を作成するときは、次のように作成できる。

float3 v0 = float3(0.1, 0.4, 2.3);
float3 v1 = float3(.1, .2, .34); // 小数値の整数部分は省略できる。

この例では、x, y, zの順にfloat3の値を指定している。

また、Swizzllingという書法を用いれば、ベクトルの要素の一部を操作できる。

float3 v0 = float3(.1, .3, .6);
float2 u0 = v0.xy; // float2(.1, .3);
float2 u1 = v0.yz; // float2(.3, .6);
float2 u2 = v0.zz; // float2(.6, .6);
v0.rg += .5; // v0 = float3(.6, .8, .6);

他の型については後ほど必要に応じて紹介する。

セマンティクス

POSITION, SV_POSITION, SV_TARGETなどはセマンティクスと呼ばれ、頂点シェーダーやフラグメントシェーダの関数による値の受け渡しの間で、その値がどういう情報か指定するものである。
POSITIONはメッシュの頂点の位置座標。4次元ベクトルであるが、4つ目の値は演算上の都合で存在。常に1が入る。
SV_POSITIONはフラグメントシェーダに渡すScreen空間に変換されたメッシュの頂点の位置座標。
SV_TARGETは出力する画面上の色。RGBAを指定する。( Red, Green, Blue, Alpha(透明度) )

値の意味をセマンティクスによって指定するため、逆に変数名は自由に設定できる。
例えば今回はvertexという変数名が長いと感じ、vにしてしまったとしてもいい。

セマンティクスについてまとめた次のページが参考になる。
Unityのシェーダーセマンティクスまとめ

また、もっと詳しくはUnityのドキュメントやMicrosoftのHLSLのドキュメントを読むと良い。
シェーダーセマンティクス - Unity Documentation
Semantics - Microsoft Document

vert関数の中のUnityObjectToClipPos関数はなにをしているか

このシェーダーはUnityのシーン上に配置したオブジェクトのメッシュを表示するために使われる。
その時、vert関数の入力のvertexのxyzの値には、メッシュのオブジェクト空間の座標が入っている。
オブジェクト空間の座標とは、メッシュデータに記された頂点の座標のことである。

fragの返り値の型はfloat4だけど実際に1を返しているのは？

スカラー値はベクトル型、行列型に暗黙的にキャストできる。
その時、そのベクトル/行列の値はすべてそのスカラー値になる。
したがって、今回は返り値としてfloat4(1, 1, 1, 1)になる。
この値では、rgbaの値がすべて1になり、白色の表示になる。

Shaderで絵を描く

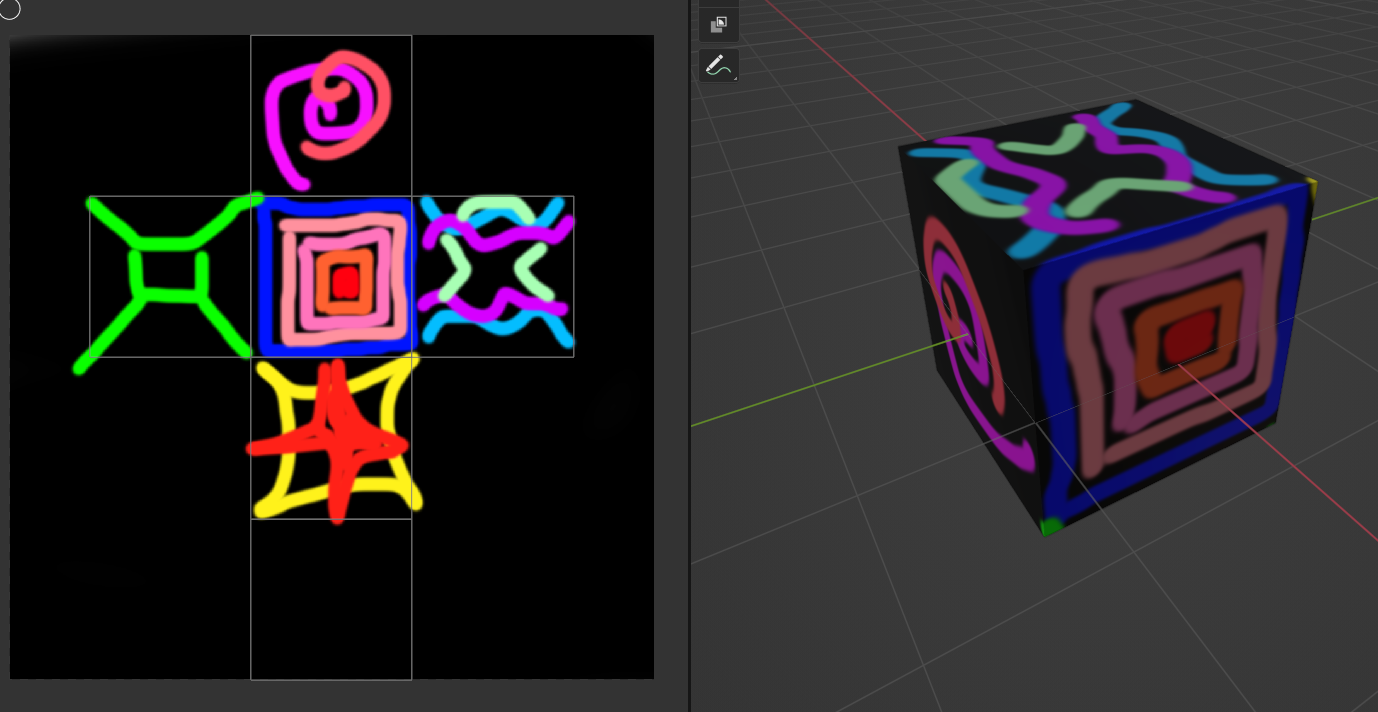
先ほどの白を表示するだけのシェーダーに手を加えて、絵を描く。
今回の目標は次の画像を表示できるようにすること。
この画像を書くためには、ほとんど内容が同じなシェーダーの入門ページがあるのでリンクを載せておく。
GLSL/様々な図形を描く - wgld.org

まずは準備をする。

構造体を使ったvert, frag関数の入出力

次のコードは、vert関数, frag関数の入力、出力を直接変数とセマンティクスを用いて指定せずに、構造体を定義して指定している。
セマンティクスさえ合わせれば、入出力の型は構造体で良い。

Shader "Custom/SamplePaint"
{
  SubShader
  {
    Pass
    {
      CGPROGRAM
      #pragma vertex vert
      #pragma fragment frag

      #include "UnityCG.cginc"

      // 構造体の定義
      struct appdata // vert関数の入力
      {
        float4 vertex : POSITION;
        float2 texcoord : TEXCOORD0;
      };
        
      struct fin // vert関数の出力からfrag関数の入力へ
      {
        float4 vertex : SV_POSITION;
        float2 texcoord : TEXCOORD0;
      };

      // float4 vert(float4 vertex : POSITION) : SV_POSITION から↓に変更
      fin vert(appdata v) // 構造体を使用した入出力
      {
        fin o;
        o.vertex = UnityObjectToClipPos(v.vertex);
        o.texcoord = v.texcoord;
        return o;
      }

      float4 frag(fin IN) : SV_TARGET // 構造体finを使用した入力
      {
        return 1;
      }
      ENDCG
    }
  }
}

TEXCOORDについて

ここで、texcoordという、見慣れない単語が登場している。
texcoordは、Texture Coordinateの略で、(Coordinate:座標)
メッシュ情報の中のUV座標という情報に対応する。
これは、普通、メッシュにテクスチャを貼り付けるために使用され、
メッシュ情報の中で、それぞれの頂点に対応したUV座標が存在する。
たとえば立方体の展開図を、そのままテクスチャに使うと↓の画像のようになる。
このテクスチャで、UV座標は各頂点がテクスチャ画像のどこの位置に対応するかを示す情報である。
この座標はテクスチャを貼り付けるために使うならば、(u, v)の2次元の座標で、範囲が0 ~ 1の範囲である。
画像の黒い背景のテクスチャについて、左下が(0, 0), 右上が(1, 1)である。

uv, uv2, uv3のように、UV座標は複数持つことができる。
TEXCOORD0に加えて、TEXCOORD1、TEXCOORD2を使用すれば複数のuv座標を入力できる。

struct appdata
{
  float4 texcoord : TEXCOORD0;  // uv
  float4 texcoord2 : TEXCOORD1; // uv2
  float4 texcoord3 : TEXCOORD2; // uv3
};

TEXCOORDに限らず、vertからfragに値を渡す時には、頂点単位の値からピクセル単位の値まで、
線形補間的に（つまり良い感じに）値を変換してくれる。

また、単にテクスチャを貼り付ける目的でなければ、uv座標は0 ~ 1の範囲外でも使うことができる。
そして、Shader内で、vert関数からfrag関数へ値を渡すときに、TEXCOORDのセマンティクスを使うと、自由な値を渡すことができる。
ただし、Shaderのターゲットレベルによって、使用できるTEXCOORDの数は変わる。
(ターゲットレベルが高いシェーダーは古いGPUでは使用できないことがある。ターゲットレベルは、#pragma target 4.0のように記述して指定できる。最近のPCで実行する前提であれば、たぶん気にする必要はない。)

詳しくは、次のリンクの、interpolatorの数(vertからfragに渡せる値の数(floatの数))に書かれている。
シェーダーコンパイルターゲットレベル - Unity Documentation
また、MicrosoftのHLSLのDocumentも参考になる。
Semantics - Microsoft Document

CGINCLUDE/ENDCG

今度は、Shaderが書きやすくなるように、SubShaderの上の行に、少し追加するものがある。

Shader "Custom/SamplePaint"
{
CGINCLUDE

float4 paint(float2 uv)
{
  return 1;
}

ENDCG
  SubShader
  {
    Pass
    {
      CGPROGRAM
      #pragma vertex vert
      #pragma fragment frag

      #include "UnityCG.cginc"

      // 構造体の定義
      struct appdata // vert関数の入力
      {
        float4 vertex : POSITION;
        float2 texcoord : TEXCOORD0;
      };
        
      struct fin // vert関数の出力からfrag関数の入力へ
      {
        float4 vertex : SV_POSITION;
        float2 texcoord : TEXCOORD0;
      };

      // float4 vert(float4 vertex : POSITION) : SV_POSITION から↓に変更
      fin vert(appdata v) // 構造体を使用した入出力
      {
        fin o;
        o.vertex = UnityObjectToClipPos(v.vertex);
        o.texcoord = v.texcoord;
        return o;
      }

      float4 frag(fin IN) : SV_TARGET // 構造体finを使用した入力
      {
        return paint(IN.texcoord.xy);
      }
      ENDCG
    }
  }
}

3行目から数行、SubShaderの上に、CGINCLUDE ~ ENDCGを挿入した。
この中のpaint関数を後でfrag関数から呼び出して出力にしている。

CGINCLUDE ~ ENDCGに書かれたHLSLは、SubShader内のHLSLよりも先に実行される。
そのため、ここで必要な関数を定義して使うことができる。

Pass内のプログラムでは、ほぼほぼ常にインデントが3つ以上下がるため、
演算に必要な処理はCGINCLUDE ~ ENDCGに書いた方が書きやすい。
また、レンダリングにおいて、正常に描画をするために、複数回別の種類のShaderのプログラムを走らせることが多い。
このようなときには、Passを複数書き込むことになるが、
CGINCLUDE ~ ENDCGに関数を定義しておけば、複数のPass間で共通の処理を関数呼び出しだけで済ますことができる。

また、コードに示されているように、frag関数等とは別に関数を用意しておけば、
実際にShaderのプログラムを考えて書いている間に、
appdataやfinの構造体のような、余計な情報を考慮する必要が無くなる。

ところで、CGINCLUDE ~ ENDCGを書く場所は意外と自由に書けちゃったりする。
SubShaderの中に書いても、後述するPropertiesの中に書いても問題なく動作してしまう。
まあ、Shaderの括弧の中に書けばいいよね。

今後は、paint関数のみを書きかえて説明していく。

単色の表示

まずは、簡単にテキトーな色を表示させる。
次のように書きかえる。

float4 paint(float2 uv)
{
  float3 col = float3(0, 1, .5);
  return float4(col, 1);
}

すると、Cubeの表示が次のようになり、色が変わることが確認できる。

col変数に、r=0, g=1, b=.5の値を入れて、青緑色になっている。

時間による色の変化

次に、時間によって色を変化させる。

float4 paint(float2 uv)
{
  float t = _Time.y;
  float3 col = float3(
    sin(t*2.), 
    sin(t*1.2+1.3),
    sin(-t*2.1-2));
  col = col * .5 + .5;
  return float4(col, 1);
}

このように書きかえて、Unityの画面からシーンを再生すると、Cubeの色が時間によって変化することが確認できる。

Unityのプログラムが開始されてからの時間は_Time.yで取得できる。
参考:ビルトインのシェーダー変数 - Unity Documentation

また、sinの値域は(-1 ~ 1)であるため、* .5によって (-.5 ~ .5)の範囲にし、+ .5によって(0 ~ 1)の範囲にしている。

UV座標の使用

次に、uv座標を用いたShaderを書く。
まずは、uv座標の値をそのまま、rとgに出力してみる。

float4  paint(float2 uv)
{
  return float4(uv, 0, 1);
}

すると、Cubeは次のようになる。

黄色になっているところは、r=1, g=1, b=0の色である。
UnityのCubeにおいては、それぞれの面についてuv座標が(0, 0)から(1, 0), (0, 1), (1, 1)までの値を取ることがわかる。

ここから、Cubeではなく、Quadを用いることにする。

Quadは見てわかる通り、左下が(0, 0)で右上が(1, 1)のuv座標を持つ、四角いメッシュによってできている。

テクスチャを貼り付ける

ここで、少し寄り道をしてテクスチャを貼り付けるシェーダーを書く。

Shader "Custom/SamplePaint"
{
  Properties
  {
    _Tex ("Tex", 2D) = "" {}
  }
CGINCLUDE

sampler2D _Tex;

float4 paint(float2 uv)
{
  return tex2D(_Tex, uv);
}
ENDCG
~~~ 以下省略 ~~~

Properties

Propertiesを使用することで、Unityのマテリアルの設定画面で値を指定することができるようになる。
記述の仕方は、次のようになる。

Properties
{
  変数名 ("表示するラベル名", プロパティのタイプ) = デフォルト値 // この行を必要なだけ
}

ここで、指定した変数名と同じ名前の変数がCGINCLUDEもしくはCGPROGRAM内に宣言されていれば（関数の外で）、
その変数にマテリアルから指定した値が入ってきて、使うことができる。

プロパティのタイプは主に、Integer, Float, Vector, Color, 2Dなどがある。
加えて、Range(a, b)とすると、aからbまでのレンジスライダーを使用できる。
プロパティについてはここで説明するより、Unityのドキュメントで。
ShaderLab: マテリアルプロパティの定義 - Unity Documentation

tex2D

sampler2D型の変数を関数の外に宣言しておき、プロパティから設定できるようにしておく。
tex2D(texture, uv)に値を渡すことで、uv座標からテクスチャの色を読み取ることができる。

テキトーにドット絵を描いて、貼り付けてみた。(ドット絵のできには目を瞑ってほしい)

座標の原点を中心に持っていく。

今回は、図の真ん中を中心とした図形を描こうとしている。
今の座標は左下を原点としたものなので、座標の原点を中心に持っていく。

float4 paint(float2 uv)
{
  float2 p = uv*2. - 1.;
  return float4(p, 0, 1);
}

uvに2を掛けることで、画面上に写る座標の範囲が(0 ~ 1)から(0 ~ 2)になる。
更に、1を引くことで範囲は(-1 ~ 1)になる。

すると、Quadは次のようになる。

左下が(-1, -1)、右下が( 1, -1)、左上が(-1, 1)、右上が( 1, 1)、中心が(0, 0)の座標になった。
0未満の値は正しく表示できないので、左下は黒く塗りつぶされている。

中心からの距離を表示

まずは、円を描くところから始める。
その前段階として、中心からの距離をそのまま表示してみる。

length関数を使うことで、ベクトルの長さを計算できる。

float4 paint(float2 uv)
{
  float2 p = uv*2. - 1.;
  float d = length(p);
  return d;
}

ベクトルpは中心が原点となる平面座標の値である。
このベクトルの距離を取れば、すなわちそれが中心からの距離となる。

距離が1以上の部分は、白で表示されている。

円を描く

中心からの距離を取る

中心から半径rの円を描くことを考える。
まずは、先ほどの中心からの距離について考える。

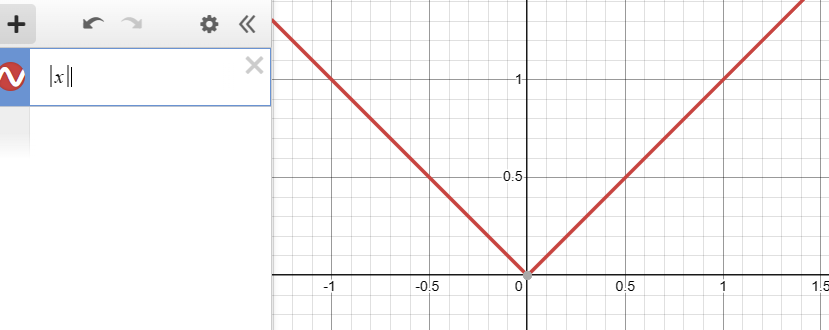
次のグラフは、先ほどのプログラムのpによる座標系において、
y=0、つまりx軸上(上の画像の赤線のところ)での、変数dの値を表したものである。

円を描く

Shaderにおいて、座標から図形の境界線を算出するときには、数式上で計算結果が0になる値に着目する。
半径がr=0.5であるならば、このグラフで考えると、x=0.5のときに、0になるようにすればよい。
0.5を引くと、ちょうどx=0.5, -0.5のときにグラフの値が0になる。
座標の中で、計算結果が0になる値で形をつくる関数を距離関数と言う。
変数dの名前は、距離(distance)からとっている。

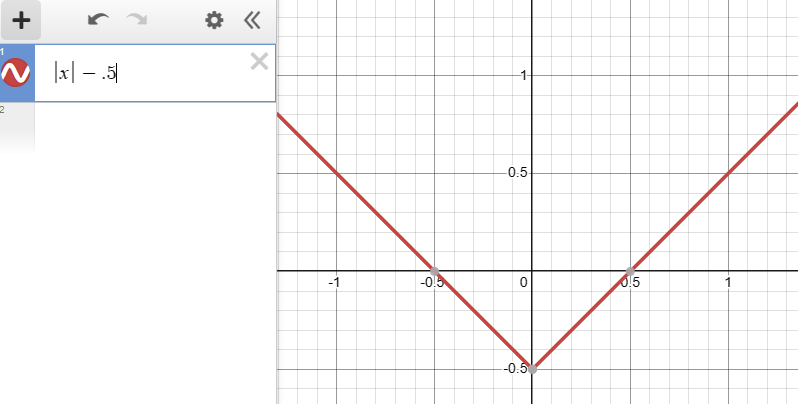
(画像はグラフ描画ツールのDesmosより)

この値をShaderに持ってきて、計算したdの値が、半径が0.5の円のところで0になるようにする。

float4 paint(float2 uv)
{
  float2 p = uv*2. - 1.;
  float d = length(p) - .5;
  return d;
}

そうすると、先ほどのグラフの値がそのまま色の明るさとなるため、円の内側は負の値なので、中心から半径0.5の黒い円が表示される。

円の境界線を取る

今回は、境界線に注目したいので、次のようにさらに絶対値を取ることで、境界線をはっきりさせる。

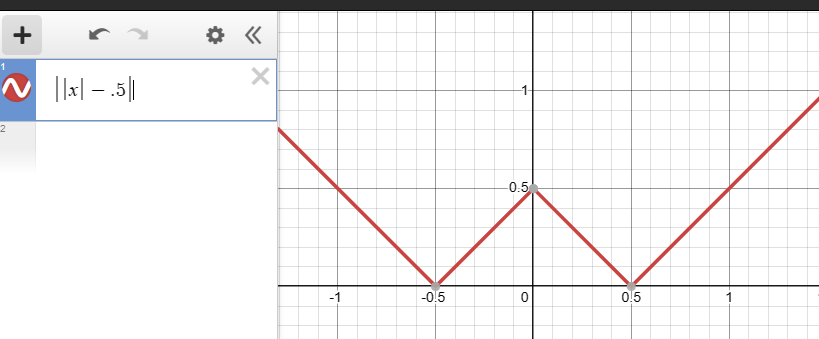
絶対値は、HLSLではabs関数を使う。

float4 paint(float2 uv)
{
  float2 p = uv*2. - 1.;
  float d = length(p);
  d = abs(d-.5);
  return d;
}

円の境界線を光らせる

今の状態では、円の境界線が暗くなってしまっている。
これをかっこよく光らせる。
綺麗に光らせるために、反比例のグラフを使える。

反比例のグラフy = abs(1/x)は、xが0に近づくほど、無限に近い値になる。

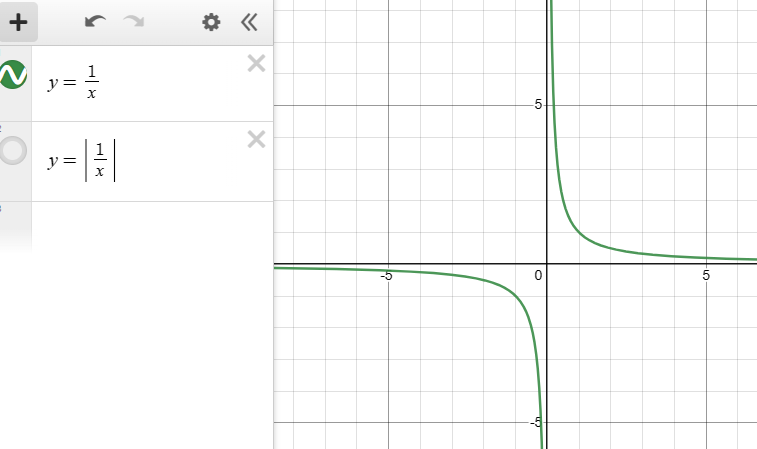
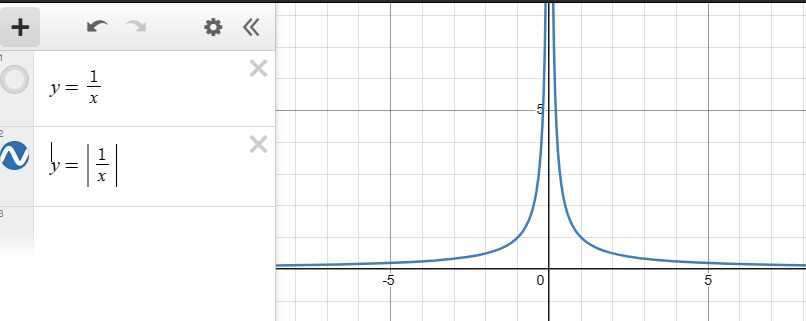
先ほどの、変数dの値は、0のところで円を形作っている。
このdの値に、反比例を適応すれば、円の境界線が光ることになる。

float4 paint(float2 uv)
{
  float2 p = uv*2. - 1.;
  float d = length(p) - .5;
  float b = 0.01 / abs(d); // Brightness
  return b;
}

波を作る（花みたいになる）

距離関数をいじって円の形に波を作る。
atan2(y, x)という関数を使えば、座標上のベクトルの角度がラジアンで取れる。
試しに、atan2の値をそのまま出力してみる。
すると、atan2によって角度が(-π ~ π)の範囲で算出されているのがわかる。

// 定数PIの定義
#define PI 3.14159265

float4 paint(float2 uv)
{
  float2 p = uv*2. - 1.;
  float theta = atan2(p.y, p.x);
  return theta / PI;
  float d = length(p) - .5;
  float b = 0.01 / abs(d);
  return b;
}

この値を使用して、sinを使って、波を作る。sinの値域が(-1 ~ 1)であることに注意する。
ついでに、色も付けた。

float4 paint(float2 uv)
{
  float2 p = uv*2. - 1.;
  float theta = atan2(p.y, p.x);
  float d = length(p) - .5 + sin(theta*6.) * .4;
  float b = 0.005 / abs(d);
  float3 col = float3(.1, .01, 1.);
  return b * col;
}

このように、角度によって円の半径を変えることで、円に波がついて花のような形になる。

花の回転

角度thetaをもとに、sinを介して波を作っている。
このsinに渡す値に、時間を加算することでこの花を回転させられる。

float4 paint(float2 uv)
{
  float2 p = uv*2. - 1.;
  float theta = atan2(p.y, p.x);
  float d = length(p) - .5 + sin(theta*6. + _Time.y*.5) * .4;
  float b = 0.01 / abs(d);
  float3 col = float3(.5, .0, 1.);
  return float4(b * col, 1);
}

花の光の関数化

この花の形の光を表現するコードを、関数化して再利用できるようにする。
その関数は、円の半径や波の大きさ、波の数、回転の角度などを指定できるものにする。
まず、準備として、コード内で使用しているマジックナンバー（直接書き込まれている数値）の中、
円の半径、波の大きさ、波の数、回転の角度や速度などを変数に置き換える。

float4 paint(float2 uv)
{
  float n = 6.;
  float radius = .5;
  float angle = _Time.y*1.5;
  float waveAmp = .4;
  float3 col = float3(.1, .01, 1.);

  float2 p = uv*2. - 1.;
  float theta = atan2(p.y, p.x);
  float d = length(p) - radius + sin(theta*n + angle) * waveAmp;
  float b = 0.01 / abs(d);
  return float4(b * col, 1);
}

次に、置き換えた変数を引数とする関数flowerを作る。
この時、色は後から掛けるだけでいいので、関数内では扱わないうえに、返り値もfloatでいい。

作った関数flowerを使用して、paint関数で複数の花を表示する。

float flower(float2 p, float n, float radius, float angle, float waveAmp)
{
  float theta = atan2(p.y, p.x);
  float d = length(p) - radius + sin(theta*n + angle) * waveAmp;
  float b = 0.01 / abs(d);
  return b;
}

float4 paint(float2 uv)
{
  float2 p = uv*2. - 1.;

  float3 col = 0;
  col += flower(p, 6., .9, _Time.y*1.5, .1) * float3(.1, .01, 1.);
  col += flower(p, 3., .2, PI*.5-_Time.y*.3, .2) * float3(1., .5, 0.);
  col += flower(p, 4., .5, _Time.y*.3, .1) * float3(0., 1., 1.);

  // 薄い緑色の花
  col +=
    min( flower(p, 18., .7, -_Time.y*10., .01), 1.) * .1 *
    float3(.1, .6, .1);

  col += flower(p, 55., .05, _Time.y*100., .1) * float3(1., .1, .1);
  return float4(col, 1);
}

このように、色情報の加算によって、複数の花を描くことができた。
1つ、薄い緑色の花については、flower関数によって算出された値に手を加えている。
まず、私はこの線だけを暗めにしたかった。
そのため、まず、算出された値に0.1を掛けてみたが、画像で比較するように、光の線が細くなるだけであった。

反比例のグラフをそのまま小さくしても、形は変わらないので当然ではある。

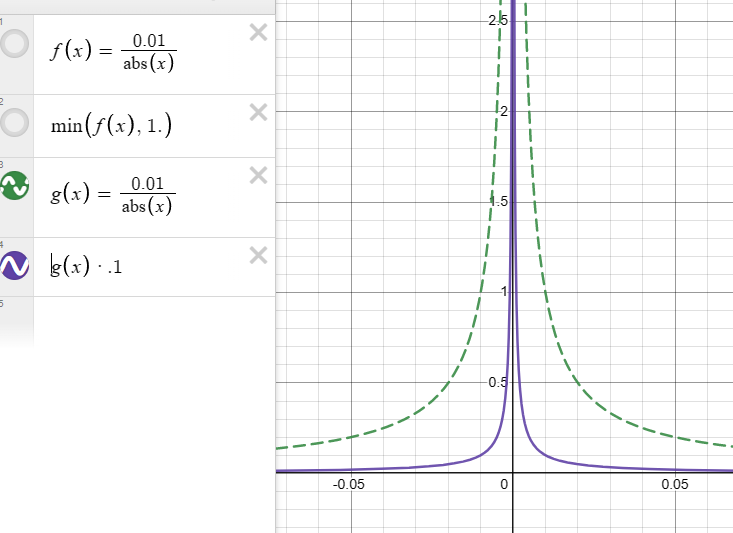
そこで、min関数を使用した。
min関数は、渡された2つの値の小さいほうを取得できる。
これを使うことで、値に最大値としての制限を設定できる。

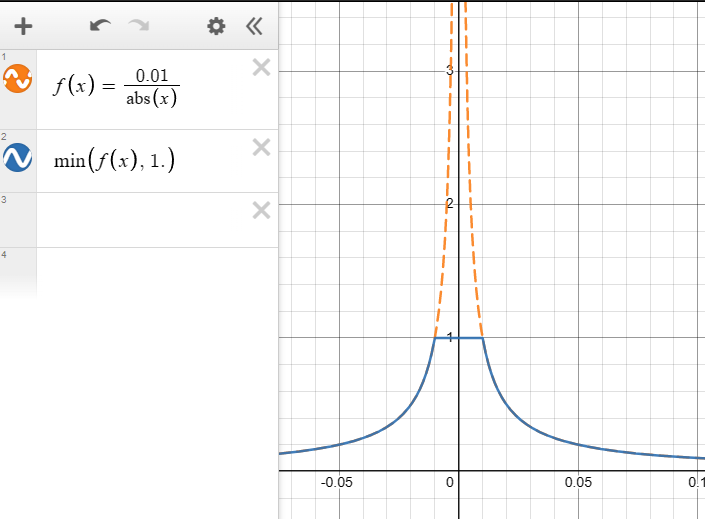
(画像は数式グラフ描画ツールDesmosより)

少し微調整をして完成

float flower(float2 p, float n, float radius, float angle, float waveAmp)
{
  float theta = atan2(p.y, p.x);
  float d = length(p) - radius + sin(theta*n + angle) * waveAmp;
  float b = 0.006 / abs(d); // 光の強さをちょっと強くした
  return b;
}

float4 paint(float2 uv)
{
  float2 p = uv*2. - 1.;
  p *= 1.1; // ちょっと座標を拡大して図形を相対的に小さくする

  float3 col = 0;
  col += flower(p, 6., .9, _Time.y*1.5, .1) * float3(.1, .01, 1.);
  col += flower(p, 3., .2, PI*.5-_Time.y*.3, .15) * float3(1., .2, 0.);
  col += flower(p, 4., .5, _Time.y*.3, .07) * float3(0., .6, .8);
  col +=
    min( flower(p, 18., .7, -_Time.y*10., .01), 1.) * .1 *
    float3(.1, .6, .1);
  col += flower(p, 55., .05, _Time.y*100., .1) * float3(1., .1, .1);
  return float4(col, 1);
}

その2ではどんな話するか？

座標の扱いとか距離関数とかについて詳しめに話す予定。たぶん
それかsurfaceシェーダーについて話すかもしれない。未定

参考になるリンク

リンク集など

• 2019年度GLSLお役立ちシート - Qiita
  GLSLの紹介記事？のような感じ。
  GLSL投稿サイトの紹介とか、GLSLの入門記事とか、リンクがいろいろと載っている。

Shaderの作品が見れるサイト

• ShaderToy
• GLSL Sandbox

シェーダーのプロパティについて

• 【シェーダー勉強④】Propertiesについて - ツクロウヤ
  画像付きでまとめられているので、わかりやすい。

• ShaderLab: マテリアルプロパティの定義 - Unity Documentation

• Cg/HLSL でシェーダープロパティを参照する - Unity Documentation

セマンティクスについて

• Unityのシェーダーセマンティクスまとめ - Qiita
• シェーダーセマンティクス - Unity Documentation
• Semantics - Microsoft Documentation

HLSLの組み込みの関数について

• Shader(HLSL), 手続き的にテクスチャ生成など行うとき使用頻度の高い関数 - Qiita
  画像付きでわかりやすいけど、すべてを網羅しているわけではない。
• HLSL Intrinsic(組み込み) Functions - Microsoft Documentation
  公式の情報なので、すべての組み込み関数について調べられる。
• GLSLをHLSLに書き換える
  GLSLとHLSLの関数対応表

入門記事とか

• The Book of Shaders(日本語)
• GLSL Contents - wgld.org
  GLSLの入門記事の一覧。Shaderの書き方について、基本的なことがまとめられているので、学び始めの頃に参考になった。

その他(追記)

• Inigo Quilez :: articles
  Inigo Quilezさんの記事一覧。
  英語だけど関数一覧とか、シェーダーを書く上でためになる情報がてんこ盛りのサイト