Shaderを使ってプロシージャルにモデルやテクスチャを作成する時, 把握しておくと便利な関数があります.
基本的には, TEXTURING&MODELING A Procedural Approach 3rd Edition (https://www.amazon.co.jp/Texturing-Modeling-Procedural-Approach-Third/dp/4862460860) のCHAPTER2冒頭の内容です.詳しくはこちらの書籍を参照されてください.
補間関数
lerp
線形補間を行う関数
float lerp(float a, float b, float x)
{
return a + x * (b - a);
}
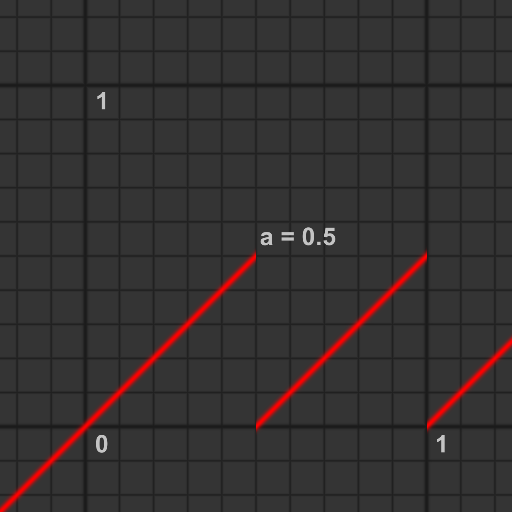
xが0のとき, 結果はa, xが1のとき, 結果はbとなります. xが0.5のとき, 結果は0.5 * a + 0.5 * b, xが0.7の時, 0.3 * a + 0.7 * bとなり, xの値を0→1すると, 結果は線形にa→bと変化します.
条件関数
step
2つの値を比較して, どちらの値が大きいかに基づいて 0 または 1 を返します.
float step(float a, float x)
{
return (float) (x >= a) ? 1 : 0;
}
xがa以上の場合は1, それ以外は0を返します.
ifの書き換え
GPUアーキテクチャの特性上, if文の多用はパフォーマンスを落とす要因となり得ます.
lerp関数とstep関数を用いて if文は以下のように書き換えることができます.
if (u < 0.5)
{
color = fixed4(1.0, 1.0, 1.0, 1.0);
}
else
{
color = fixed4(0.0, 0.0, 0.0, 0.0);
}
↓↓↓
color = lerp(fixed4(1.0, 1.0, 1.0, 1.0), fixed4(0.0, 0.0, 0.0, 0.0), step(0.5, u));
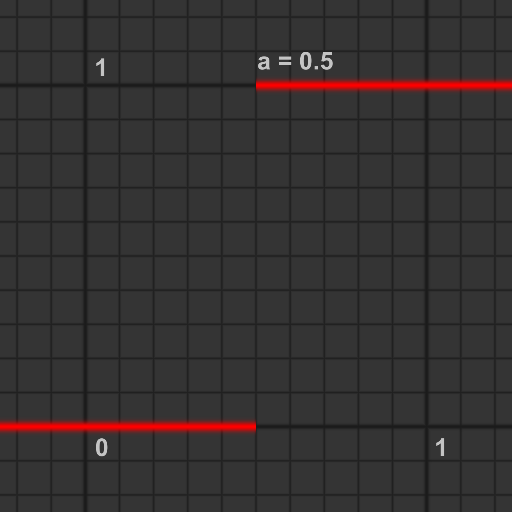
step関数で作られる矩形パルス関数
2つのstep関数を組み合わせて, 次のような矩形パルスが作成できます.
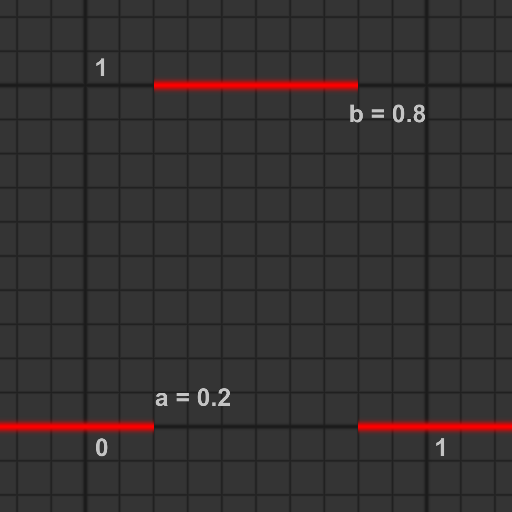
#define PULSE(a, b, x) (step((a),(x)) - step((b),(x)))
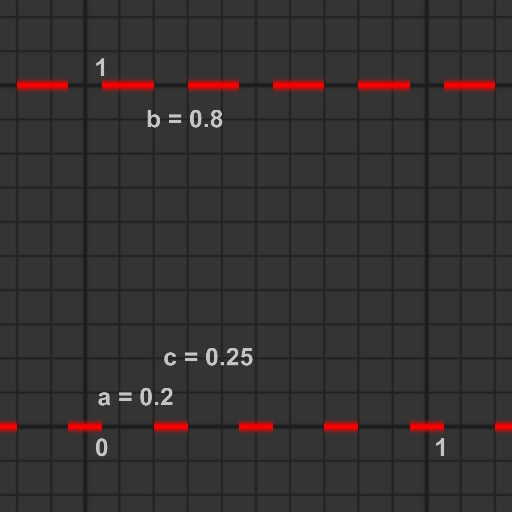
グラフは以下のようになり, aで始まりbで終わるパルスを生成します.
clamp
指定された値を指定された最大値と最小値の範囲に留めます
float clamp(float x, float a, float b)
{
return (x < a ? a: (x > b ? b : x));
}
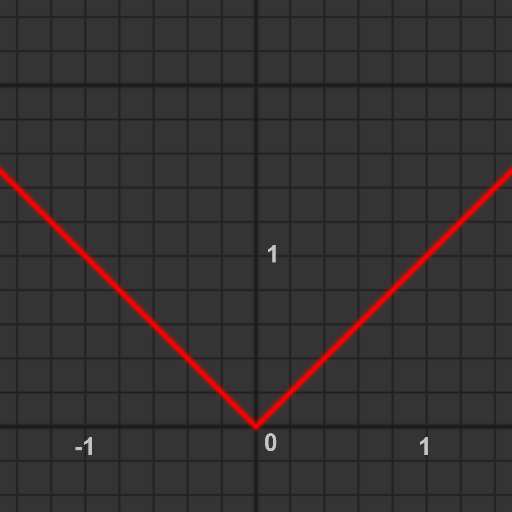
abs
指定された値の絶対値を返します.
float abs(float x)
{
return (x < 0 ? -x : x);
}
グラフは以下のようになります.
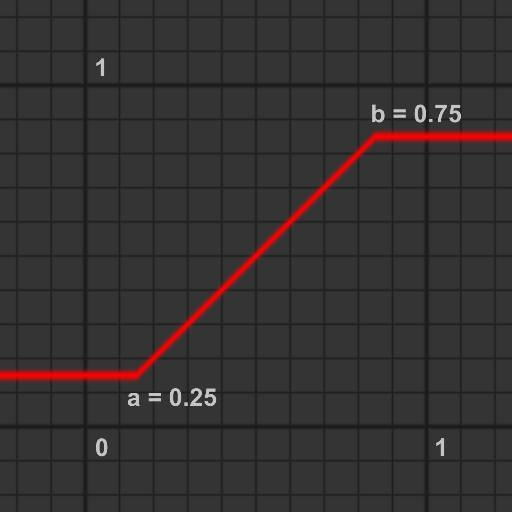
smoothstep
閾値aで始まり, 閾値bで終わる緩やかな遷移を作ります.
smoothstepは, aとbのときに傾きが0, aのとき値が0, bのとき値が1となる特性を持つ3次関数 $3x^2-2x^3$ で実装されます.
float smoothstep(float a, float b, float x)
{
float t = saturate((x - a)/(b - a));
return t * t * (3.0 - (2.0 * t));
}
グラフは以下のようになります.
周期関数
sin
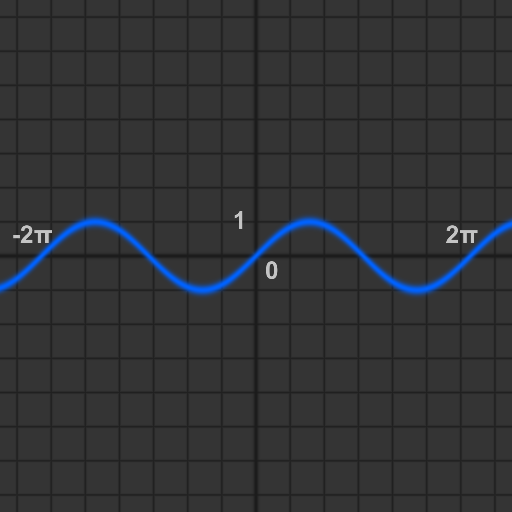
正弦波を返します. 0で始まり, xを[0, 2π]と変化させると[-1, 1]の範囲で値が変化します.
グラフは以下のようになります.
cos
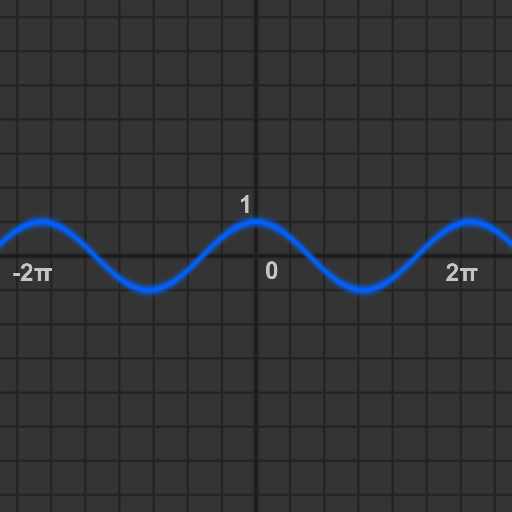
余弦波を返します. 1で始まり, xを[0, 2π]と変化させると[-1, 1]の範囲で値が変化します.
グラフは以下のようになります.
fmod
aをbで除算したときに得られる正の剰余が得られます.
float fmod(float a, float b)
{
int n = (int)(a / b);
a -= n * b;
if (a < 0)
{
a += b;
}
return a;
}
以下のようなグラフが得られます.
fmod(x, a) / aとすると,振幅1, 周期がaののこぎり波が得られます.
これと
#define PULSE(a, b, x) (step((a),(x)) - step((b),(x)))
を組み合わせることによって, 周期cのパルス関数が得られます
PULSE(a, b, fmod(x, c) / c)
補正系関数（非組み込み関数）
単位区間で単調増加する関数を区間内での値のゆがみを変化させます.
ガンマ補正関数
float gammacorrect(float gamma, float x)
{
return pow(x, 1.0 / gamma);
}
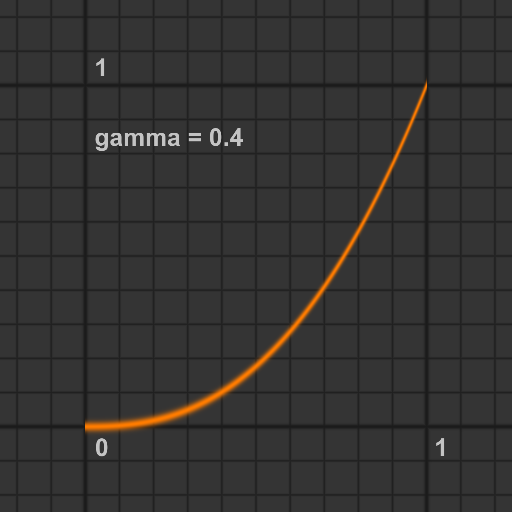
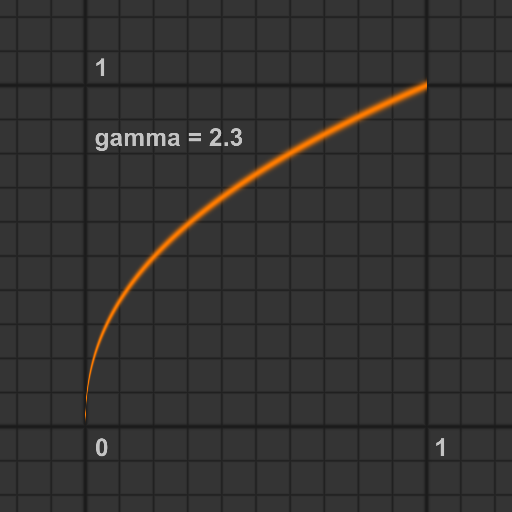
gammaが1より大きければ, 1に向かって上方向にシフトし, gammaが0と1の間であれば0に向かって下方向にシフトします.
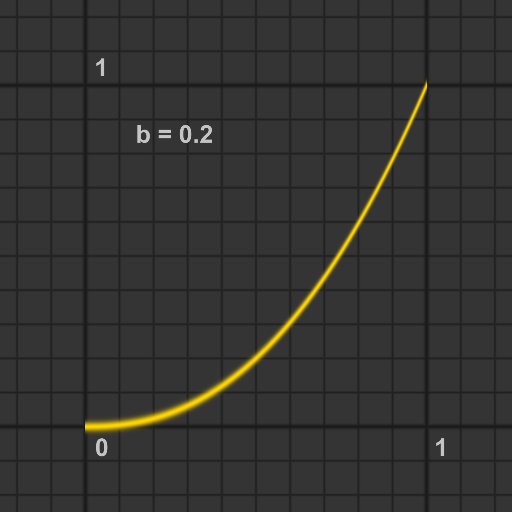
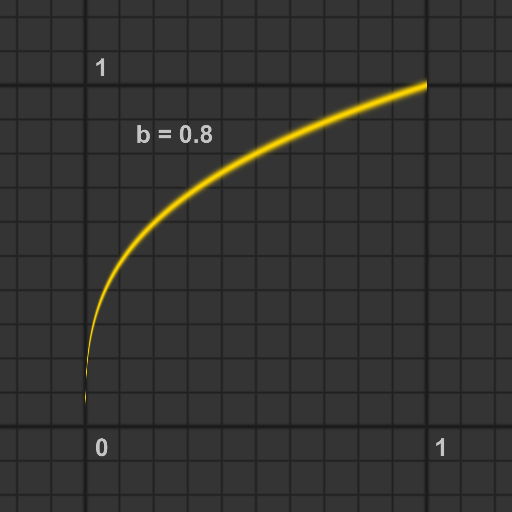
bias関数
bias関数はガンマ補正関数のバージョンの一つで, bias(b, 0.5) = bとなるように定義されたパラメータ b で, gammaパラメータを置き換えます.
float bias(float b, float x)
{
return pow(x, log(b) / log(0.5));
}
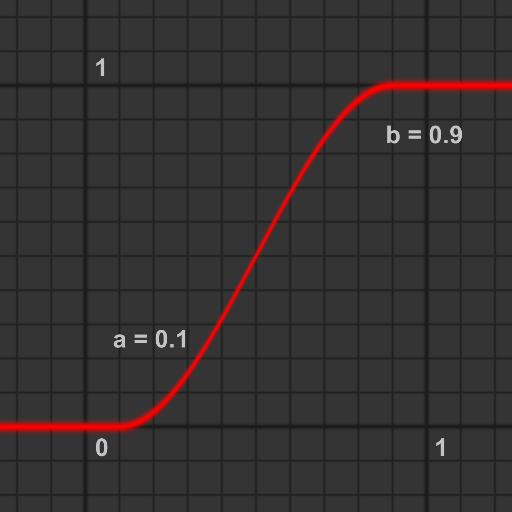
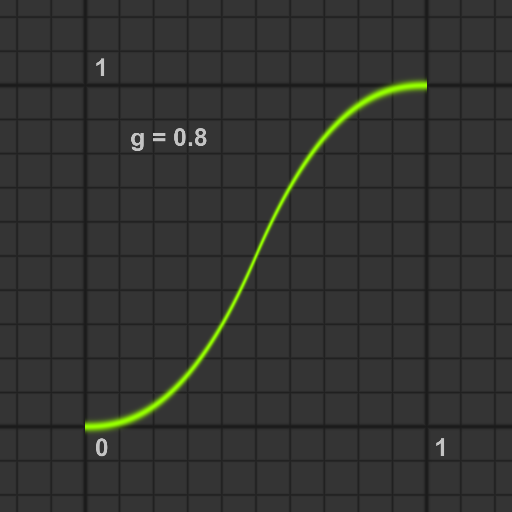
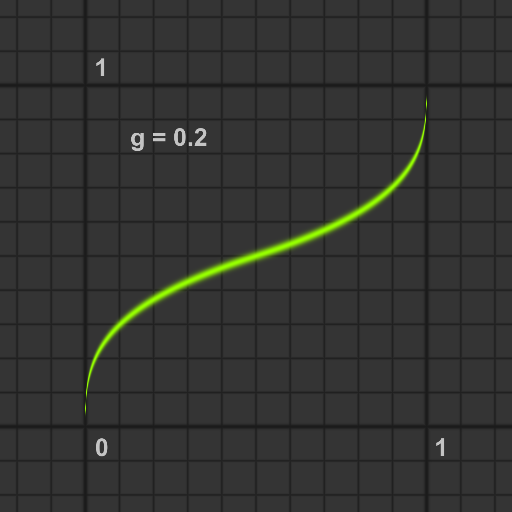
gain関数
gの値によらずxが0.5のとき0.5を返す, bias曲線で形成されたS字曲線を返します.
float gain(float g, float x)
{
if(x < 0.5)
{
return bias(1.0 - g, 2.0 * x) / 2.0;
}
else
{
return 1.0 - bias(1.0 - g, 2.0 - 2.0 * x) / 2.0;
}
}
