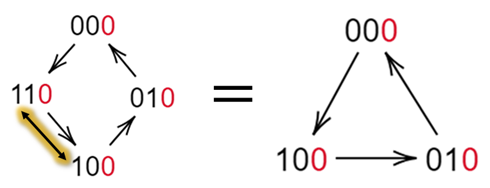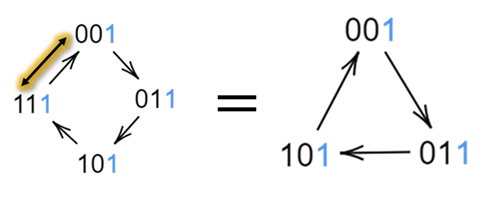量子ウォークの量子コンピュータ実装3 ~サイクル3上アダマールウォーク~

サイクル $3$ 上のアダマールウォークの実装をまとめる．量子ウォークの量子コンピュータ実装2でサイクルサイズが$2^n$の場合を紹介したが，サイクルサイズが$2^n$でない場合も紹介する．簡単なサイクルサイズである$3$を実装する．
ここで紹介する方法は，Efficient quantum circuit implementation of quantum walksに同様．

サイクル3上 Hadamard Walk について

量子ウォークの簡単な説明は量子ウォークの量子コンピュータ実装1を参考．

今回考えるサイクルは，

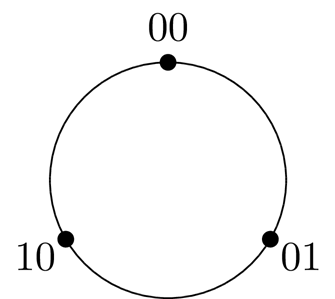
である．このサイクル（ $00,01,10$ (10進数で0~2))上の量子ウォークを定義する

コイン作用素とシフト作用素

全体のダイナミクスとして，
$$
W=\hat{S}\hat{C}\
$$
で表す．コイン作用素，シフト作用素を以下で表す．

コイン作用素 $\hat{C}$

\hat{C}=(I\otimes H)\\
\mbox{ただし}I=\sum_{x}|x\rangle\langle x|,\quad
H=\frac{1}{\sqrt{2}}\begin{bmatrix}
1&1\\1&-1
\end{bmatrix}

シフト作用素 $\hat{S}$

\hat{S}=\sum_{x}|x-1\rangle\langle x|\otimes|0\rangle\langle 0|+|x+1\rangle\langle x|\otimes|1\rangle\langle 1|

とする．ただし，$x\pm 1$は$mod3$で考える．

初期状態 $$\Psi=\frac{1}{\sqrt{2}}|0\rangle\otimes|0\rangle+\frac{i}{\sqrt{2}}|0\rangle\otimes|1\rangle$$

このコイン作用素とシフト作用素のゲートを考えれば，量子ウォークの時間発展を量子ウォークを表現できる．

具体的には，
コイン作用素 $\hat{C}=I\otimes H$ は，状態の量子ビットだけに$H$を通せば表せる．
シフト作用素 $\hat{S}$は，
・状態が0ならば場所xが-1
・状態が1ならば場所xが+1
するゲートを考えればよい．

IBMQでの実装

今回の実装には 3qubits($q[0]q[1]q[2]$)を使う．場所(00,01,10)に対応する qbit として $q[0]q[1]$ を，状態に対応する qubit として $q[2]$ を考える．

シフト作用素の構築(サイクル3について)

$n$桁2進数の+１操作と-１操作のアルゴリズムを考えたいが，$q[0]q[1]$には$11$も含まれているので，それをうまく排除する必要がある．そこで，サイクル４上の量子ウォークのシフト(量子ウォークの量子コンピュータ実装1)を基本にして，関係ないサイクルを除く Switch 部分を加える．

-1 操作(状態は0)
サイクル４の-1操作$+$場所11と10のスイッチ$=$サイクル３の-1操作

+1 操作(状態は１)
サイクル４の+1操作$+$場所11と00のスイッチ$=$サイクル３の+1操作

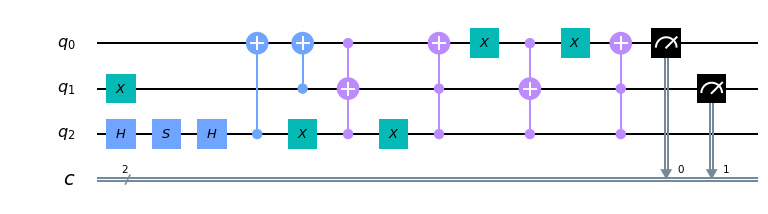
以上をまとめるとシフト作用素は，

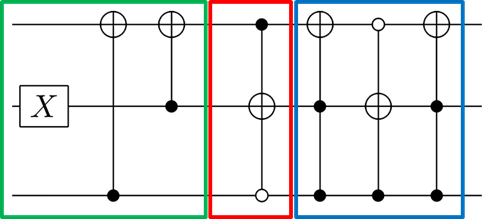
となる．
サイクル4のシフト作用素+状態0なら場所11と10スイッチ+状態1なら場所11と00スイッチ

回路部分の作成

量子レジスター、古典レジスター、そしてそれらから量子回路qwqcを設定

場所qbits $\Rightarrow q[0]q[1]$
状態qbits $\Rightarrow q[2]$

from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import execute

from qiskit.tools.visualization import plot_histogram

q = QuantumRegister(3, 'q')
c = ClassicalRegister(2, 'c')

qwqc = QuantumCircuit(q,c)

#時間
t=1

#初期状態をセット
qwqc.h(q[2])
qwqc.s(q[2])

#時間発展
for i in range(t):
    #コインオペ
    qwqc.h(q[2])
    #シフト
    qwqc.x(q[1])
    qwqc.cx(q[2],q[0])
    qwqc.cx(q[1],q[0])
    #-1回転の修正
    qwqc.x(q[2])
    qwqc.ccx(q[0],q[2],q[1])
    qwqc.x(q[2])
    #+1回転の修正
    qwqc.ccx(q[1],q[2],q[0])
    qwqc.x(q[0])
    qwqc.ccx(q[0],q[2],q[1])
    qwqc.x(q[0])
    qwqc.ccx(q[1],q[2],q[0])

#観測
qwqc.measure(q[0],c[0])
qwqc.measure(q[1],c[1])

qwqc.draw()

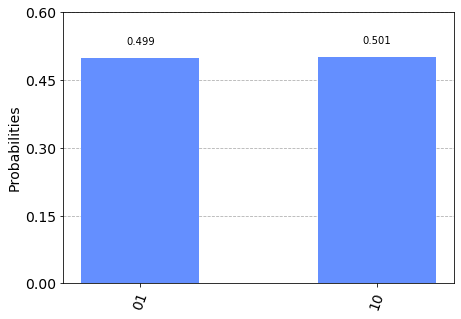
t=1でのシミュレーターの結果

from qiskit import BasicAer
backend_s=BasicAer.get_backend('qasm_simulator')
job_s = execute(qwqc, backend_s,shots=1024)
result_s = job_s.result()
counts_s = result_s.get_counts(qwqc)
plot_histogram(counts_s)

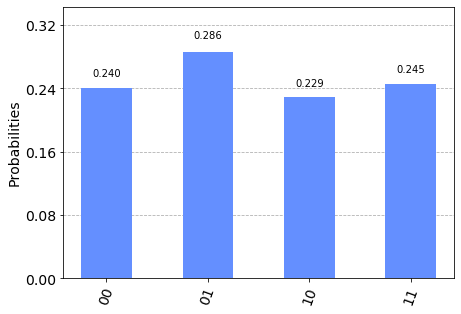
t=1での実機の結果

from qiskit.tools.monitor import job_monitor
provider = IBMQ.get_provider(hub='ibm-q')

backend_r=provider.get_backend('ibmqx2')
job_r = execute(qwqc, backend=backend_r,shots=1024)
job_monitor(job_r)

Job Status: job has successfully run

result_r= job_r.result()
counts_r = result_r.get_counts(qwqc)
plot_histogram(counts_r)

まとめ

これと同じ様にすることで，任意のサイクルサイズ上での量子ウォークを実装することができる．任意サイクルnの実装のために，$n\leq 2^N$となる最小の$N$について，サイクル$2^N$のシフトを量子ウォークの量子コンピュータ実装2の方法で作り，スイッチ操作で修正することで，任意サイクルが作れる．