量子ウォークの量子コンピュータ実装1 ~サイクル4上アダマールウォーク~
量子ウォークの研究をする横国大の今野研所属の数学系大学院生です.研究室のメンバーと2017年から量子情報の勉強をはじめ.2018年からはIBM Qを用いて実装もおこなってきました.これまでの量子アルゴリズムや量子ウォークの実装に関するノートが貯まってきたこともあり,せっかくなので順次まとめる.
今回は,サイクル4上のアダマールウォークの実装を行う.
ここで紹介する方法は,Efficient quantum circuit implementation of quantum walksとほぼ同様である.
サイクル4上 Hadamard Walk について
量子ウォーク
量子ウォークは,ランダムウォークの量子版として導入された.ランダムウォークとの違いは,確率の時間発展ではなく,確率振幅の時間発展を考えること,そして確率振幅のノルム2乗をとることで確率になるという点です.数学の解説本として「量子ウォーク」,また数学から物理学,工学,情報科学までまとめた「量子ウォークの新展開~数理構造の深化と応用~」などがある.
簡単な説明とともにモデルの定義をしていく.
今回考えるサイクルは,
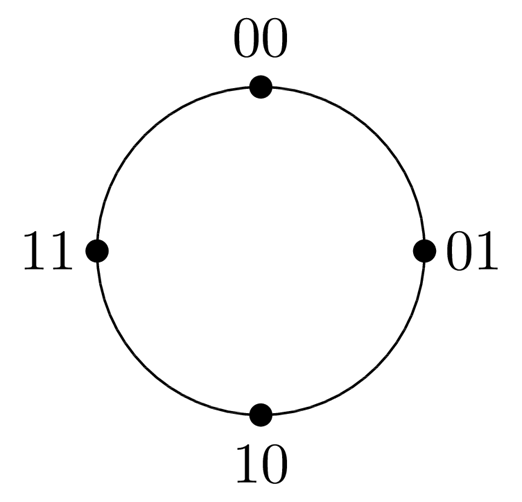
である.このサイクル($00,01,10,11$(10進数で0~3))上の量子ウォークを以下で定義する.
- 量子コイン(アダマール行列)
U=\frac{1}{\sqrt{2}}\begin{bmatrix}
1&1 \\
1&-1
\end{bmatrix}
ここで,
P=\frac{1}{\sqrt{2}}\begin{bmatrix}
1&1 \\
0&0
\end{bmatrix}\\
Q=\frac{1}{\sqrt{2}}\begin{bmatrix}
0&0 \\
1&-1
\end{bmatrix}
とする.
- 初期状態
\Psi(0)=\frac{1}{\sqrt{2}} \begin{bmatrix}1\\i\end{bmatrix}, \Psi(1)=\Psi(2)=\Psi(3)=\begin{bmatrix}0\\0\end{bmatrix}
ただし,$\Psi(x)$は場所$x$の確率振幅である.
- 時間発展
量子ウォークの時間発展は,確率振幅の時間発展になる.
\begin{align}
\Psi(x)=&P\Psi(x+1)+Q\Psi(x-1)\\
=&\frac{1}{\sqrt{2}}\begin{bmatrix}
1&1\\0&0
\end{bmatrix} \Psi(x+1)+\frac{1}{\sqrt{2}}\begin{bmatrix}
0&0\\1&-1
\end{bmatrix}\Psi(x-1)
\end{align}
ただし,$x+1,x-1$はサイクル上なので$mod4$で考える.
- 観測
確率振幅のノルム2乗を取ることによって,確率が得られる.
\mu(x)=\|\Psi(x)\|^2
コイン作用素とシフト作用素
上の表現はダイナミクスの理解はしやすいが,実装するために系全体のダイナミクスとして,
$$
W=\hat{S}\hat{C}\
$$
で表す.それぞれの作用素は以下で表す.
- コイン作用素$\hat{C}$
\hat{C}=(I\otimes H)\\
\mbox{ただし,}I=\sum_{x}|x\rangle\langle x|,\quad H=\frac{1}{\sqrt{2}}\begin{bmatrix}
1&1\\1&-1
\end{bmatrix}
- シフト作用素$\hat{S}$
\hat{S}=\sum_{x}|x-1\rangle\langle x|\otimes|0\rangle\langle 0|+|x+1\rangle\langle x|\otimes|1\rangle\langle 1|
とする.また,
- 初期状態
$$\Psi=\frac{1}{\sqrt{2}}|0\rangle\otimes|0\rangle+\frac{i}{\sqrt{2}}|0\rangle\otimes|1\rangle$$
で表せる.
このコイン作用素とシフト作用素のゲートを考えれば,量子ウォークの時間発展を量子ウォークを表現できる.
具体的には,
コイン作用素 $\hat{C}=I\otimes H$ は,状態の量子ビットだけに $H$ を通せば表せる.
シフト作用素 $\hat{S}$ は,
・状態 が0ならば場所 $x$ が減算
・状態 が1ならば場所 $x$ が加算
するゲートを考えればよい.
IBMQでの実装
今回の実装には 3qubits ($q[0]q[1]q[2]$) を使う.場所 (00,01,10,11) に対応する qbit として$q[0]q[1]$を,状態に対応する qubit として $q[2]$ を考える.
シフト作用素の構築(サイクル4について)
天下り的だが,2桁2進数 $q[0]q[1]$ と状態 $q[2]$ に対して次の計算をする.
|$q[0]q[1]$場所(10進数0~3)|$q[2]$(状態0or1)||$(q[0]\oplus\overline{q[1]}\oplus q[2])(\overline{q[1]})$ |
|:---:|:---:|:---:|:---:|:---:|
|00|0|$\Rightarrow$|11|
|01|0|$\Rightarrow$|00|
|10|0|$\Rightarrow$|01|
|11|0|$\Rightarrow$|10|
|00|1|$\Rightarrow$|01|
|01|1|$\Rightarrow$|10|
|10|1|$\Rightarrow$|11|
|11|1|$\Rightarrow$|00|
表のように,入力: $q[0]q[1]q[2] \Rightarrow$ 出力: $(q[0]\oplus\overline{q[1]}\oplus q[2])(\overline{q[1]})(q[2])$ と組むと,状態が0なら減算,状態が1なら加算になっており,シフト作用素に対応している.この出入力を量子回路で実装すればよいことになる.
回路部分の作成
量子レジスター、古典レジスター、そしてそれらから量子回路qwqcを設定
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import execute
from qiskit.tools.visualization import plot_histogram
q = QuantumRegister(3, 'q')
c = ClassicalRegister(2, 'c')
qwqc = QuantumCircuit(q,c)
時間発展部分
# 時間発展回数
t=1
# 初期状態をセット
qwqc.h(q[2])
qwqc.s(q[2])
# 時間発展
for i in range(t):
#コイン作用素
qwqc.h(q[2])
#シフト作用素
qwqc.x(q[1])
qwqc.cx(q[2],q[0])
qwqc.cx(q[1],q[0])
# 場所(q[0]q[1])を観測 状態(q[2])は観測しない
qwqc.measure(q[0],c[0])
qwqc.measure(q[1],c[1])
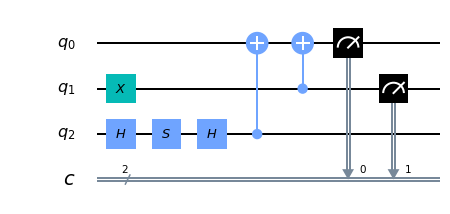
# 回路描画
qwqc.draw()
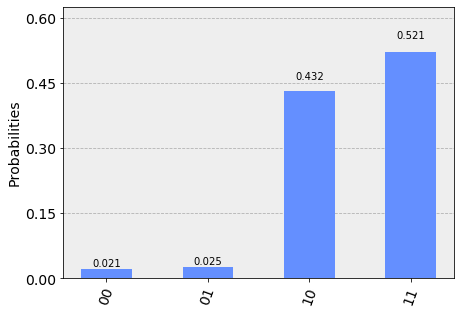
t=1でのシミュレーターの結果
from qiskit import BasicAer
backend = BasicAer.get_backend('qasm_simulator')
job = execute(qwqc, backend,shots=1024)
result = job.result()
counts = result.get_counts(qwqc)
plot_histogram(counts)
理論的には,
\begin{align}
W\Psi&=\hat{S}\times\left(|0\rangle\otimes\frac{1+i}{2}|0\rangle+|0\rangle\otimes\frac{1-i}{2}|1\rangle\right)\\
&=\frac{1+i}{2}|3\rangle\otimes|0\rangle+\frac{1-i}{2}|1\rangle\otimes|1\rangle
\end{align}
より
\mu(1)=\mu(3)=\frac{1}{2}
となる.シミュレーターなのでそこそこの結果になった.
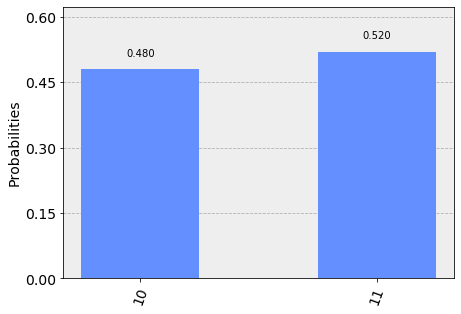
t=1での実機の結果
from qiskit import IBMQ
from qiskit.tools.monitor import job_monitor
provider = IBMQ.get_provider(hub='ibm-q')
provider.backends()
backend_r=provider.get_backend('ibmqx2')
job_r = execute(qwqc, backend=backend_r,shots=1024)
job_monitor(job_r)
Job Status: job has successfully run
result_r= job_r.result()
counts_r = result_r.get_counts(qwqc)
plot_histogram(counts_r)
まとめ
サイクル4上アダマールウォークは,回路が比較的簡単で時間発展t=1だったため,そこまでエラーも蓄積されない結果と言えるかもしれない.
また,コイン作用素のアダマール行列$H$を別のユニタリ行列$U$で置き換えると,別の空間的一様な量子コインの量子ウォークになる.IBM Qでは$U_3(\theta,\phi,\lambda)$で好きな量子コインを作れる.
今後は,他のサイクル上,他グラフ上,多状態数モデル,空間的時間的非一様モデルについても順次まとめていきたい.また量子ウォークを用いたアルゴリズムについてもまとめたい.