Go to Qiita Advent Calendar 2024 Top
LoginSignup
3
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@YNUqw(YNUqw)

3状態量子ウォークの量子コンピュータ実装

Posted at

３状態量子ウォークの量子コンピュータ実装

3状態量子ウォークの実装をまとめる．
ここまで，量子ウォークの量子コンピュータ実装3によって、任意のサイクルサイズの量子ウォークを実装してきた．しかし，そのどれもが状態として0または1のふたつしかない，2状態量子ウォークであった．そこで，状態数３の量子ウォークを考えたい．
前回同様，サイクル上量子ウォークのシフト作用素についてはEfficient quantum circuit implementation of quantum walksを参考．

3状態の量子ウォークについて

3状態量子ウォークとは内部状態が３つある量子ウォークのことをいう．特に$3\times 3$のGrover行列をコイン作用素に選んだものを，3状態Grover Walkという．詳細は，量子ウォークを参考．

具体的なダイナミクスは後で説明するとして，1次元上3状態GroverWalkの特徴は，空間的に一様なコインを配置しても原点付近の局在化と線形的な広がりが，同時に起こることである．
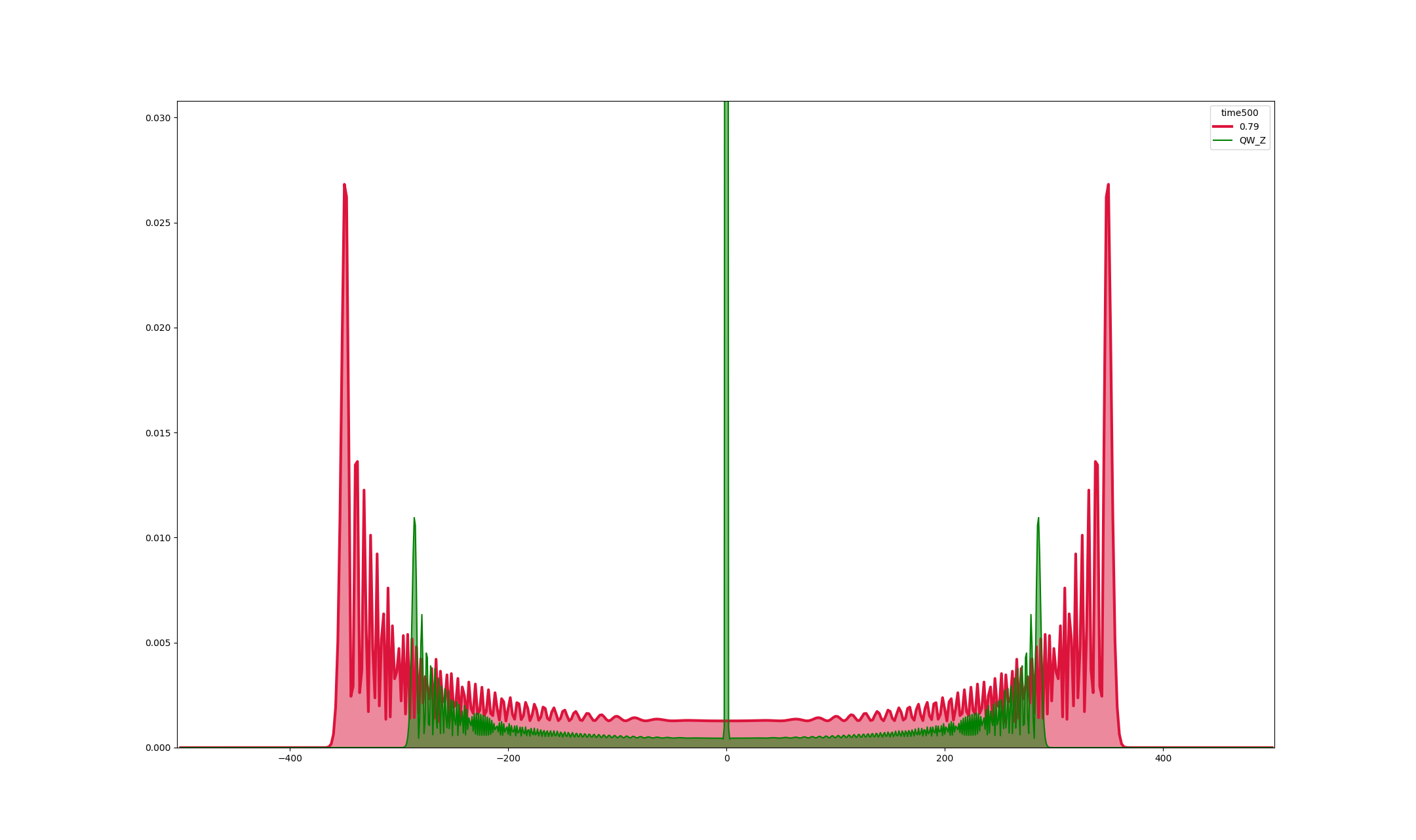
QIITAGrov.png
1次元2状態アダマールウォークと1次元3状態GroverWalkの原点出発で時刻５００の数値シミュレーションのグラフである．原点付近局在化がよくわかる．

さて、量子コンピュータで実装するには、1次元などの無限系ではなく，有限系でないといけないのでサイクル上の3状態GroverWalkを実装していく．全体の時間発展を

W=\hat{S}\hat{C}

とする．
3状態GroverWalkを考えているので，シフト作用素$\hat{C}$に，$3\times3$Grover行列

\hat{C}=I\otimes C\\
\mbox{ただし}C=\frac{2}{3}\begin{bmatrix}1&1&1\\1&1&1\\1&1&1\end{bmatrix}-I=\frac{1}{3}\begin{bmatrix}-1&2&2\\2&-1&2\\2&2&-1\end{bmatrix}

を採用する．
シフト作用素は，サイクル上の3状態(00,01,10)を考えているの，

\hat{S}=\sum_{x}(|x-1\rangle\langle x|\otimes|00\rangle \langle 00|+|x\rangle\langle x|\otimes|01\rangle \langle 01|+|x+1\rangle\langle x|\otimes|10\rangle \langle 10|)

とする．

  • 状態が00だと場所-1，
  • 状態が01だとその場に留まる
  • 状態が10だと場所+1
    をしている．

回路を考える

状態3を実装するために，2量子ビット使うと状態は00,01,10,11の４つになってしまう。したかがって、コイン作用素とシフト作用素を4状態表記に変換する。

コイン作用素

\hat{C}=I\otimes C\\
\mbox{ただし}C=\begin{bmatrix}\frac{-1}{3}&\frac{2}{3}&\frac{2}{3}&0\\\frac{2}{3}&\frac{-1}{3}&\frac{2}{3}&0\\\frac{2}{3}&\frac{2}{3}&\frac{-1}{3}&0\\0&0&0&1\end{bmatrix}

シフト作用素

\hat{S}=\sum_{x}(|x-1\rangle\langle x|\otimes|00\rangle \langle 00|+|x\rangle\langle x|\otimes|01\rangle \langle 01|+|x+1\rangle\langle x|\otimes|10\rangle \langle 10|+|x\rangle\langle x|\otimes |11\rangle\langle 11|)

このようにとると、状態11については他の状態と混じることのない、独立したものが作れる。したがって、初期状態に状態11を与えなければ、3状態の量子ウォークの実装になっている。

#　回路作成

Grover行列

$4\times 4$行列の中に$3\times 3$のGrover行列を作る。ここは計算によってパラメータを調べた結果だけ紹介する。

import numpy as np
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import execute
import math

th1=3*math.pi/2
th2=(math.pi+math.acos(1/3))*2
th3=math.pi/2

q = QuantumRegister(2, 'q')

grqc = QuantumCircuit(q)
grqc.x(q[0])
grqc.x(q[1])
grqc.cu3(th3,0,0,q[0],q[1])
grqc.cu3(th2,0,0,q[1],q[0])
grqc.cu3(th1,0,0,q[0],q[1])
grqc.x(q[0])
grqc.x(q[1])

このようにゲートを作ると$4\times 4$のなかに$3\times 3$のGroverコインができる．以下で確認をしておく．

from qiskit import BasicAer

# unitary simulator backend で実行
backend = BasicAer.get_backend('unitary_simulator')
job = execute(grqc, backend)
result = job.result()

# Show the results
print(result.get_unitary(grqc, decimals=3))

[[-0.333+0.j 0.667+0.j 0.667+0.j 0. +0.j]
[ 0.667+0.j -0.333+0.j 0.667+0.j 0. +0.j]
[ 0.667+0.j 0.667+0.j -0.333+0.j 0. +0.j]
[ 0. +0.j 0. +0.j 0. +0.j 1. +0.j]]

回路実装 ​

量子レジスター、古典レジスター、そしてそれらから量子回路を考える．

def cccx(circ,c1,c2,c3,tg,re):
    circ.ccx(c1,c2,re)
    circ.ccx(c3,re,tg)
    circ.ccx(c1,c2,re)

cccnotゲートを使いたいので準備したら，回路を作る．

from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import execute
from qiskit.tools.visualization import plot_histogram
import math

q = QuantumRegister(2, 'q')
qc = QuantumRegister(2, 'qc')
qaf = QuantumRegister(1,'qaf')
c = ClassicalRegister(2, 'c')

gqc = QuantumCircuit(q,qc,qaf,c)

th1=3*math.pi/2
th2=(math.pi+math.acos(1/3))*2
th3=math.pi/2

#時間
t=1

#初期状態をセット
gqc.x(qc[1])
gqc.barrier()
#時間発展
for i in range(t):
    #coin-ope
    gqc.x(qc[0])
    gqc.x(qc[1])
    gqc.cu3(th3,0,0,qc[0],qc[1])
    gqc.cu3(th2,0,0,qc[1],qc[0])
    gqc.cu3(th1,0,0,qc[0],qc[1])
    gqc.x(qc[0])
    gqc.x(qc[1])
    gqc.barrier()
    #shift-ope cycle
    gqc.x(qc[1])
    cccx(gqc,q[1],qc[0],qc[1],q[0],qaf[0])
    gqc.ccx(qc[0],qc[1],q[1])
    gqc.x(qc[1])
    gqc.x(qc[0])
    gqc.x(qc[1])
    gqc.ccx(qc[0],qc[1],q[1])
    cccx(gqc,q[1],qc[0],qc[1],q[0],qaf[0])
    gqc.x(qc[0])
    gqc.x(qc[1])
    gqc.barrier()
    
#観測
gqc.measure(q,c)

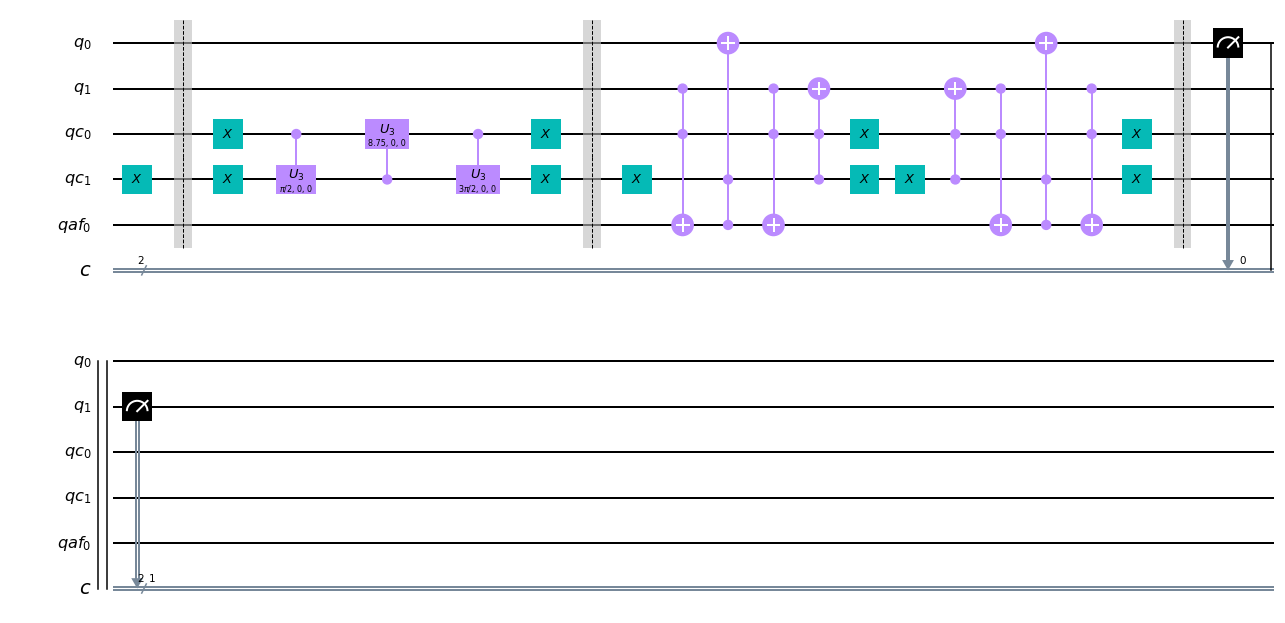
gqc.draw()

image.png

最初の部分で，初期状態をつくる．今回は

\Psi=|00\rangle\otimes|01\rangle

を作る。
2つ目の部分が，状態の部分がコイン作用素.
3つ目の部分が，「状態10なら場所+1，状態00なら場所-1，状態01,11なら場所は変わらない」というシフト作用素を表現している．

以上をシミュレータで実行する．

provider=IBMQ.get_provider(group='open')
backend_cs=provider.get_backend('ibmq_qasm_simulator')
job_cs = execute(gqc, backend_cs,shots=4096)
result_cs = job_cs.result()
counts_cs = result_cs.get_counts(gqc)
print(counts_cs)
plot_histogram(counts_cs)

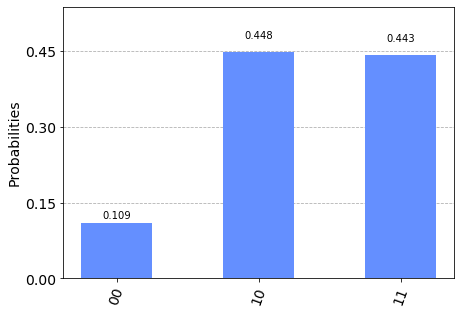
image.png

このシミュレーション結果は，

\hat{S}\hat{C}|00\rangle\otimes|01\rangle\\
=\hat{S}\left\{|00\rangle\otimes\frac{2}{3}|00\rangle+|00\rangle\otimes\frac{-1}{3}|01\rangle+|00\rangle\otimes\frac{2}{3}|10\rangle\right\}\\
=\frac{2}{3}|11\rangle\otimes|00\rangle+\frac{-1}{3}|00\rangle\otimes|01\rangle+\frac{2}{3}|01\rangle\otimes|10\rangle

より，場所$11$，$00$，$01$の観測確率は，それぞれ$\frac{4}{9}$，$\frac{1}{9}$，$\frac{4}{9}$となるはずなので，正しくシミュレーションできたとわかる．

補足

状態を多くして，それに対応したコイン作用素とシフト作用素を作りあげることで，任意のグラフ上での量子ウォークを実装することができる．トーラス上4状態量子ウォークが，サイクル上2状態量子ウォークの簡単な応用で作れる．

冒頭に紹介した，1次元上Groverの原点付近での停留項は，サイクル16で時刻7くらいまで発展させると，量子コンピュータのサイクル上での実験でも確認できる．

3
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?