お久しぶりです。
引っ越しが終わってやっと Qiita を思い出して気づいたら 2 ヵ月くらい放置してました。
どうも復活した Xu です。
たまにはちょっと変わった話をしたくて、今日は数学に近い話をしようと思います。
早速ですが、
log_2(1+\frac{M}{2^{23}})
皆さんはこの数式に見覚えありますか?
知らなくても大丈夫です、当方もつい最近知りました。
この式は高速逆平方根と呼ばれるものです。
高速逆平方根
高速逆平方根(Fast inverse square root)計算は、与えられた x に対する 1/√x の近似値を高速計算するアルゴリズムです。
主な応用は、3D グラフィックスの計算で必要な「ベクトル長」の逆数を高速に求めるために使われ、これによりゲームなどのリアルタイム描画のパフォーマンスを向上させます。
具体的には、3D グラフィックスでは、曲面は無数の平面によって組み合わされ、光を当てた際にどのように反射するか、ベクトル計算にて活用されております。
NVIDIA や Intel などのグラフィックボードでは、ハードウェアレベルで逆平方根の計算を最適化させており、実際にコードベースで実装することはなかなか見かけないかと思います。
一見難しそうですが、どうか皆さんも一緒に高校・大学の数学を一緒に思い出しながら深堀していきましょう!
解説 1. ルートの逆数
まずは基本概念を復習しましょう。
理学系の方以外は特に学生時代専門的に学ぶタイミングはなかったかと思いますが。
逆数は、簡単に言うと分母と分子を交換するだけです。
ルートの逆数は分母にルートを置きます、分子の 1 のルートは 1 なのでまあ当たり前ですよね。
例:
\sqrt{2}\ の逆数は \frac{1}{\sqrt{2}}
ここまでは簡単ですよね。
解説 2. ニュートン法
早速ですが、
質問 1. 計算機を使わずに、小数点以下 7 桁まで求めよ
\sqrt{2}
この問題は y=x^2-2 とx 軸の接点を求める問題に変換できます。

しかし、このグラフは曲線です。
計算を簡略化するために、補助線 x=2 (赤線)を作り、曲線と交差した点で接線を作ります。
接線の方程式 y−f(a)=f´(a)(x−a) により、微分法で計算すると、y=4x-6 (黄線)が求められます。

これにより、接線と x 軸の接点は (1.5, 0) が求められます。
かなり曲線と x 軸の接点が近くなりましたが、まだ若干距離ありますよね。
ここでさらに (1.5, 0) から上に線を引きます(紫線)。

ここからさらに交差した点で接線を作り x 軸との接点を計算すると、1.414667... が得られます。
これで大体の近似値が得られました。
もしもさらに精度を高めたいのであれば、上記補助線と接線を作る動作を数回繰り返してみてください。
小数点以下 7 桁までであれば 5 回ほど繰り返してもほぼ変われなくなってきます。
ざっくりな計算で十分な精度と考えられます。
これを微分積分の分野ではニュートン法と呼ばれ、300 年ほど前にかのニュートンによって発明されました。
x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}
実は高速逆平方根というのは、このニュートン法の思想に基づいて開発されました。
計算の簡略化
ここまで理解出来たら、今度はコードに落とし込むとどうなるか見てみましょう。
単純に while で回してみると、結構めんどくさいことになります。
def newtown_sqrt_2(precision=1e-7):
x = 1.0 # 初期値
while True:
next_x = 0.5 * (x * 2 / x) # ニュートン法
if abs(next_x -x) < precision:
return precision
x = next_x
しかし、実際の場面では Xn の値はどこから得られるのか?
ここで登場するのが、
世界を変えた 4 行のコード
FPS の生みの親と呼ばれる John D. Carmack 氏は、たった数行でこの計算を簡略化し、世界に革命をもたらしました。
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( * ) &i;
y = y * (threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * (threehalfs - ( x2 * y * y ) ); // 2nd iteration,
// this can be removed
return y;
}
ここで注目してほしいのはこの 4 行です。
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * (threehalfs - ( x2 * y * y ) ); // 1st iteration
何ぞやと思うかもしれませんが、順序追って説明してい行こうと思います。
解説 3. 二進数の秘密
上記で John D. Carmack 氏の話をしましたが、実は、高速逆平方根というもの自体は、氏が発明したものではなく、Greg Walsh 氏が Ardent 社に在籍中に性能が低いハードで 3D グラフィック解析を行うために発明しました。
この思想を理解するには、まずは二進数について語る必要がございます。
たとえは、以下の数を二進数に変換するにはどうしたらいいでしょうか。
3 * 10^8
3.3 * 10^{-9}
コンピューターでは、このように 32 ビット浮動小数点数を管理します。
* ******** ************************
S E M
頭の S は符号部と呼ばれ、0 はプラス、1 はマイナスとして表現され、ここでの平方根は正数のみ取り扱うため、0 で固定されます。
真ん中の E は指数部と呼ばれ、上記式で言うと、8 乗や -9 乗にあたります。
お尻の M は仮数部と呼ばれ、上記式の 3 や 3.3 にあたります。
では、例題として、
0 01111111 10000000000000000000000
を十進数に変換するとどうなるか、
S --> +
E --> 127
M --> 4194304
つまり
2^{127} * 4194304
が求められます。
と思った方、見事に引っかかりましたね!
E は 0 ~ 255 の間の整数を表現しております。
10 進数に変換したときの値 - 127 が本当の指数になります。
つまり、ここでは 127-127=0 になります。
また、科学的記数法は、実は整数部の有効数字は 1 桁のみと決められております(忘れている方多いと思います)。
整数部は 0 の場合は成立せず、小数点をさらに後ろに移動しないといけなくなります。
二進数では 0 と 1 しか存在しないため、整数部に 1 が固定されます。
ならば、そもそも 1 を単独で保存する必要はなくなってきます。
そのため、M は実は、1. 以降の小数部のみを保存しており、本来表現したい二進数は 1.10000000000000000000000 であり、これは 10 進数では 1.5 に変換できます。
よって、この二進数全体を十進数にすると、
1.5 * 2^0 = 1.5
が求められます。
このようなコンピューターの小数保存原理を数式に表すと以下になります。
y = (1+\frac{M}{2^{23}})*2^{E-127}
一見、まーーた複雑な式を出してきやがって、と思わず嘆いてしまいますよね?
Greg Walsh 氏はここから高校レベルの数学で計算を簡略化していきます。
そのあくびが終わったら気を取り直して復習しながら解説していきましょう!
解説 4. 対数について
ここで対数について復習しましょう。
y = 2^x
があるとします。
x=log_2y
が求められます。
こうすることで、徐々に数式の乗数を減らしていくことができ、複雑な乗数計算を足し算引き算にまで落とすことが可能。
しかし、対数を使うには、
log_2x
の値を知る必要があります。
では、上記でお話しした、
y = (1+\frac{M}{2^{23}})*2^{E-127}
に対して対数を求めるとどうなるか。
2^{E-127}
の部分は E-127 になりますが、
log_2(1+\frac{M}{2^{23}})
の部分は計算に困ります。
ここが氏のすごいところで、
解説 5. 困ったら図を画けって何回言ったら...
\frac{M}{2^{23}}
は性質上、 0 ~ 1 の間の数字になることは確定しています。
そこで、
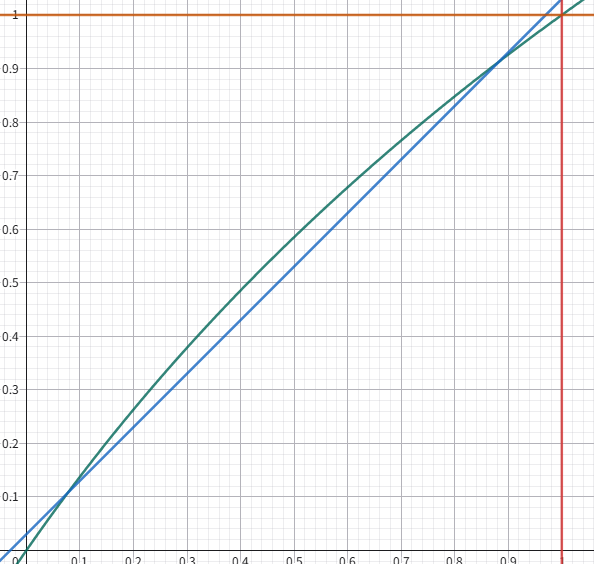
y=log_2(x+1)
と
y=x
のグラフを画き出してみると、2 本の線が交差する点は、(0,0) と (1, 0) です。
ちょうど同じ範囲ですよね。
ニュートン法の思想の元、曲線を直線に近似することができました。
log_2(1+\frac{M}{2^{23}}) \approx \frac{M}{2^{23}}
めちゃくちゃ簡単になりましたよね!
よって、
\displaylines{
log_2[(1+\frac{M}{2^{23}})*2^{E-127}] \\
= log_2(1+\frac{M}{2^{23}}) + log_22^{E-127} \\
\approx \frac{M}{2^{23}} + E -127 \\
}
これを少し変換すると以下の解が得られます。
\frac{1}{2^{23}}(2^{23} * E + M) - 127
解説 6. 次元魔法:二進数変換!
さて、上記で二進数の話をしたかと思いますが、これを見て、何かを感じたあなたは正に天才です!
十進数では、10 の乗数が増えるたびに 0 が一つ増えます。
二進数ではどうでしょうか。
\displaylines{
2^1 = 10 \\
2^2 = 100 \\
2^3 = 1000 \\
. \\
. \\
. \\
2^n = 1*10^n
}
同じように、2 の乗数が増えるたびに 0 が一つ増えます。
2^{23}*E
これは
E*10^{23}
に変換することが可能です。
ここで思い出してほしい、M はちょうど 23 桁。
つまり、浮動数 y と、その二進数 Y の関係は以下になりますよね。
log_2y = \frac{Y}{2^{23}} - 127
「なーるほど、二進数で求めた値をまた十進数に戻せば簡単な四則演算で求まるのか!
これでもう十分簡単な計算になっただろ?もういいもういい、お腹いっぱい!」
まあ落ち着けって、天才 Greg Walsh は極限までの高速化を追い求めますよ!
解説 7. さらなる簡略化
y の逆平方根を a としておくと、
log_2a = log_2y^{-\frac{1}{2}} = {-\frac{1}{2}}log_2y
として表示することが可能です。
これを 2 進数に変換すると
\displaylines{
\frac{A}{2^{23}} -127 = {-\frac{1}{2}}(\frac{Y}{2^{23}} - 127) \\
A = 381*2^{22}-{\frac{Y}{2}} \\
}
コンピューターでは、割り算は四則演算の中で最もリソースを使う計算です。
ここで、割る 2 が付く項
{\frac{Y}{2}}
は、二進数では、全体を右に一桁移動するのと同一視できます。
例: 1111100 -> 0111110
また、
381*2^{22}
は 16 進数では 5f400000 として表示されます。
「いやいやいやいやいや、待てよお前、さっきのコードと違うじゃんか!」
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
「もしかして...まだあるの???」
そうなんです、ここからが、what the fuck? なんです!
解説 8. そして神の領域へ
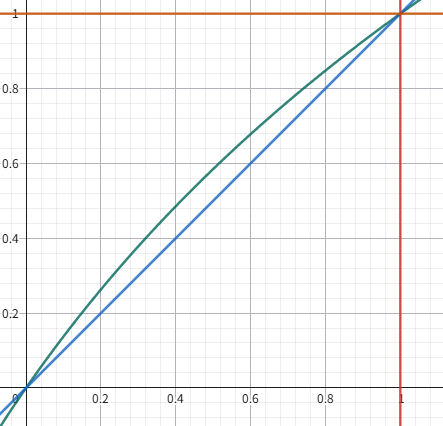
先ほどのグラフを改めて観察してみましょう。
黄色の部分(ざっくりね、ざっくり)が両グラフの誤差範囲です。
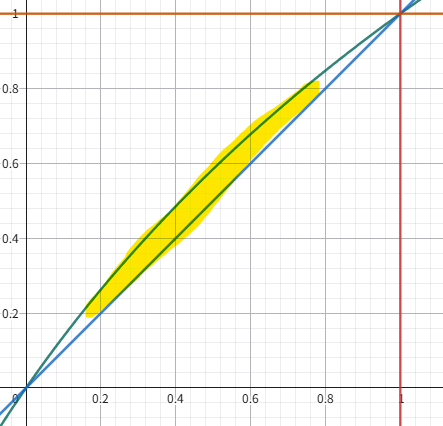
両端に近づくにつれて誤差は小さくなっていくが、真ん中あたりは拡大すると割とありますよね?
ではこの誤差を限りなく縮めるにはどうしたらいいか?
こっそり y=x をほんの少しだけ上に移動(y=x+a に)したらどうでしょうか。
ちょっと良くなったのでは?
キリいいところで交点はなくなったが、全体的に誤差は縮まった感ありますよね!
さて、その移動量(a)は果たしてどれくらいなんでしょうか?
これを 5f3759df にすると、これ以上ニュートン法を使わなくても、逆平方根の最大誤差は 5% 以下に収まり、最終的な誤差は 2/1000 以下に収まります。
実際に使う分には十分すぎますよね。
解説 9. 改めて、コードの解説
いよいよ、話を 4 行のコードに戻すと、
i = * ( long * ) &y; // evil floating point bit level hacking
まずは y を強制的に二進数計算用の long 型変数 i に変更し、
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
i に対して、引き算とビットを右に 1 桁移動する動作をし、y の逆平方根の近似値を計算し、
y = * ( float * ) &i;
long 型の i を強制的に float 型に変更し、
y = y * (threehalfs - ( x2 * y * y ) ); // 1st iteration
最終的にニュートン法で精度を高める。
これで世界を変えた 4 行のコードをご理解いただけましたでしょうか。
余談ですが、元々のコードでは、再度ニュートン法により制度をためる行もありましたが、現実的にすでに一回で十分な精度だったので、これ以上繰り返すと費用対効果が低下し、返って効率悪くなってしてしまいます。
// y = y * (threehalfs - ( x2 * y * y ) ); // 2nd iteration,
後書き
さて、ここまで読んでお気づきかと思いますが、
John D. Carmack 氏なんもしてねーじゃねーか!
Greg Walsh 氏がアルゴリズムを発明しただけやん!
と思うかもしれません。
実はこの二人は回りに回って共にこのアルゴリズムを世界に広め、科学計算ソフト、産業ソフト、グラフィック、ゲーム、そしてハードウェアにまで革命をもたらしました。
そしてかの有名な what the fuck? もおそらくこの 4 行のコードと共に今日も世界中のエンジニアに使われ、我々の身の回りで活躍しているでしょう。