お題
有名なお題であるkaggleの「House Price」問題にみんなでチャレンジしていくことになったハンズオンの内容をメモしていく企画の第6回。解説というよりはメモのまとめだったりもしますが、どこかの誰かのためになれば幸いです。前回で準備がおわり、いよいよ解析段階に。
- 元々のお題:https://www.kaggle.com/c/house-prices-advanced-regression-techniques
- 参考にした記事:https://yolo-kiyoshi.com/2018/12/17/post-1003/
本日の作業
目的変数の分布変換
- 目的変数:後輩曰く「Yですね」 → 自分「。。。」
- 目的変数:http://www.gen-info.osaka-u.ac.jp/testdocs/tomocom/express/express8.html
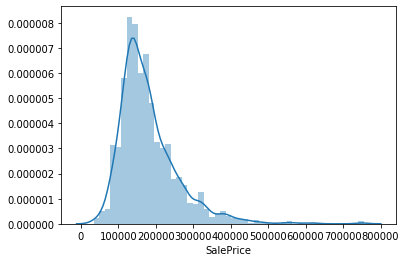
学習データのSalePrice(住宅価格)の分布を確認します。
欠損補完の箇所で、プールがない住宅がほとんどであることがわかりました。
これは裏を返せばプールがあるような豪邸がいくつか存在するということであり、住宅価格がかなり歪な分布になっているのでは?と想定されます。
こうした仮設を元に描画するのが重要だなと振り返ります。とはいえまずは言われるがままにグラフをアウトプット。
sns.distplot(train['SalePrice'])
seabornについて
「snsってなんだっけ?」ってなりました。最初過ぎて忘れていましたが、一番最初にインポートしていたライブラリの中にありましたね。これです。
import seaborn as sns
なるほどseaborn
- seaborn:どうやらグラフ描画のライブラリ。
- seaborn参照:https://qiita.com/hik0107/items/3dc541158fceb3156ee0
- distplot:seabornでヒストグラムを描画するメソッド。
train['SalePrice']に入っていた内容を確認
あとは念のため、train['SalePrice']に入っていた内容を確認。
なるほどひたすら各が並んでいる列。

アウトプットされたグラフ
そしてアウトプットされたグラフはこんな感じになりました。
sns.distplot(train['SalePrice'])
対数変換
予想どおり、かなり右側に分布の裾野が広がっています。
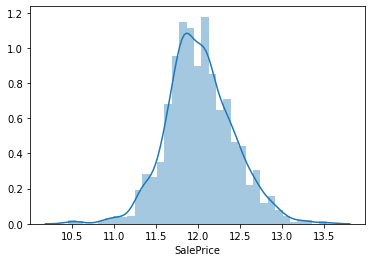
対数変換をすることで正規分布に近づけます。
とのことですが、「対数変換、とは」というところの確認。
sns.distplot(np.log(train['SalePrice']))
対数変換前後の配列の変化
これだけ出力してみます。
np.log(train['SalePrice'])
アウトプットされたグラフその2
sns.distplot(np.log(train['SalePrice']))
なるほどきれいめに正規分布になっている気がする。
予測モデルの構築
に、入りたかったですが、どうやら時間切れ臭いので今日はここまでです。
今回は変数量がかなり多いため、係数に強力なペナルティをかけたいのでLasso回帰を使って予測モデルを構築します。
予習がてらLasso回帰について調べて終了。
Lasso回帰
おしまい。
分析レイヤーに入ってきてから、やはり背景知識の補充が必要だなと、理解しました。
主に回帰分析について。