はじめに
レイトレーシングにおいて、結局のところ放射輝度とは何なのか?今までひとつずっともやもやが取れませんでした。とても重要なものさしなので、しっかり理解したいところです。なのでゼロからひとつひとつ落ち着いて紐解いて、クリアにしていきたいと思います。
光をどう捉えればいいのだろう?
現実世界はとても複雑な物理現象に満ちています。光と一口にいったって、波なのか粒子なのかといった量子力学的な話まで踏み込むととても大変です。きっと今わかっていること以外にもまだまだ隠された謎があって、これからどんどん解明されていくのでしょう。でも私達が普段目で観察できるような物体は、光の波長に比べてとてもスケールの大きな話になります。なのでレイトレーシングにおいては基本的には光のマクロ的特性だけで考えます。これはスケールの大きな世界では古典力学で日常のかなりの部分を説明できるのととても良く似ています。なので光は真空中ではまっすぐ進むし、偏光なども起きないし、回折なんかも起きない、と大胆な近似を行ってしまいます。
こんなんで物理ベースだなんだと名乗ってもいいのか?というのももっともだと思います。
しかし、
「近似」は物理でとっても大事にゃ♡鉛筆では絶対に解けない(と証明されてる)積分や方程式も極端な状況や本質的な部分に着目してそれ以外を無視する「近似」を入れると解けたりして、そしてそれでオッケーって事も多いのっ 何を重要とみなすかはその時々、物理屋の実力が問われるにゃ>< →
— 物理学科に入学した凛ちゃんbot (@RinPhysBot) 2016年7月24日
と凛ちゃんも言っているのでいいんじゃないでしょうか。
というわけで前提はこれくらいにして一つ一つ物理量を見ていきます。
Energy(エネルギー)
光はエネルギーを輸送します。エネルギーなので、これは割りと身近な単位、J(ジュール)を使います。文字としては$Q$を使うことが多いようです。
でもレイトレーシングではあまりこの単位まで降りてくることはない気がします。
Flux(放射束)
時間あたりのエネルギー、と時間が固定化されているとより明確で便利な単位になります。
Flux(放射束)というのはエネルギーを時間で微分したもので、時間あたりのエネルギー、ワットともいいます。
文字は$\Phi$
\Phi = \frac {\Delta Q}{\Delta t} = \frac {d Q}{d t}
逆にFlux(放射束)からエネルギーを知りたいときは、時間で積分を行えば良く、Flux(放射束)が定数なら単なる掛け算になります。
Q=\int { \Phi (t) } dt
Irradiance(放射照度), Radiant Exitance(放射発散度)
まずはIrradiance(放射照度)ですが、これは単位面積に到達するFlux(放射束)になります。記号は$E$を使うことが多いです。
とある面積Aに、とあるFlux(放射束)$\Phi$が到達していたとすると、平均Irradiance(放射照度)は、Flux(放射束)割る面積で求められます。
E_{average} = \frac {\Phi}{A}
もちろん先程の話と同様に微分で定義することができます。
E=\frac { d\Phi }{ dA } \\ \Phi =\int _{ A }^{ }{ E(p)dA }
カメラはレンズの後ろに光を計測できるイメージセンサが敷き詰められており、これらはIrradiance(放射照度)を求めているとも言えます。
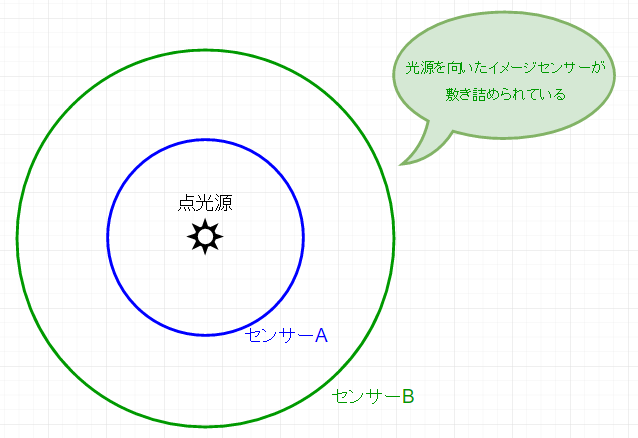
ここでやや唐突ですが、ある点光源から合計Flux(放射束)$\Phi$だけ一様に光が全方向に対して出ている状況を考えます。
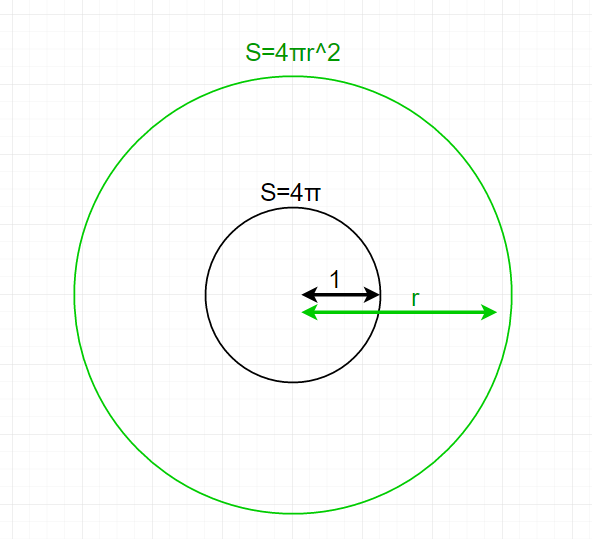
そしてイメージセンサがその点光源の周りを隙間なく囲っていて点光源を見ているとします。球型のイメージセンサは2グループ(A, B)あって、片方は半径1, もう片方はrだとします。
この状況で、それぞれのイメージセンサーは、どういうIrradiance(放射照度)を示すでしょうか?
Irradiance(放射照度)というのは面積あたりのFlux(放射束)なわけですから、イメージセンサーの面積を考えればよさそうです。球体の面積Sと半径rの関係は、
S = 4 \pi r^2
ですので、それぞれのセンサーグループが指し示すIrradiance(放射照度)は、
E_A = \frac{\Phi}{4 \pi} \\
E_B = \frac{\Phi}{4 \pi r^2}
となり、まさしくこれはライトから受ける光が距離の2乗に反比例することを示しています。
これは直観的にも納得できることでしょう。
まあすごく当たり前ですがついでにIrradiance(放射照度)に面積をかける、すなわち面積で積分すると、元のFlux(放射束)に戻ることも確認しておきます。
\Phi_A = \frac{\Phi}{4 \pi} 4 \pi = \Phi \\
\Phi_B = \frac{\Phi}{4 \pi r^2} 4 \pi r^2 = \Phi
Radiant Exitance(放射発散度)については、Irradiance(放射照度)と逆で、逆にFlux(放射束)が出て行く量を考えるだけです。こちらは$M$がよく使われます。
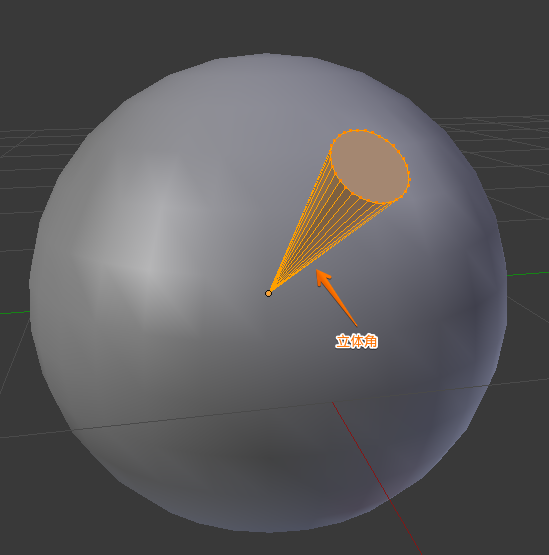
Steradian(立体角)
2次元の角度の単位にラジアンがありますが、このSteradian(立体角)は2次元の角度の自然な拡張になっています。
単位円の円弧が、ラジアンと一致するように、
単位球の表面積(球弧??)が、Steradian(立体角)と一致します。
なので、全方位の立体角が$4 \pi$であり、半球の立体角は$2 \pi$になります。
Intensity(強度)
せっかく立体角がわかったので、立体角あたりのFlux(放射束)を考えてみましょう。こちらは$I$がよく使われます。
微分をつかって表現すると、
I = \frac{\Delta \Phi}{\Delta \omega} = \frac{d \Phi}{d \omega}
となり、
例えば、全方位に一様に光を発射する点光源のIntensity(強度)は、
I = \frac{\Phi}{4 \pi}
と表現できます。
また、Intensity(強度)を立体角で積分すると、Flux(放射束)に戻ります。
\Phi =\int _{ \Omega }^{ }{ I(\omega) d\omega }
でもあまり点光源以外では使われないらしいです。
Radiance(放射輝度)
Irradiance(放射照度)にさらに方向で微分したものがRadiance(放射輝度)になります。
L = \frac{\Delta E}{\Delta \omega} = \frac{d E}{d \omega} \\
L = \frac {d^2 \Phi}{d A d \omega}
これによりある方向(ある微小立体角)からの光、もしくはある方向(ある微小立体角)への光を考えることができるようになります。
ここでRadiance(放射輝度)の性質を垣間見るために、
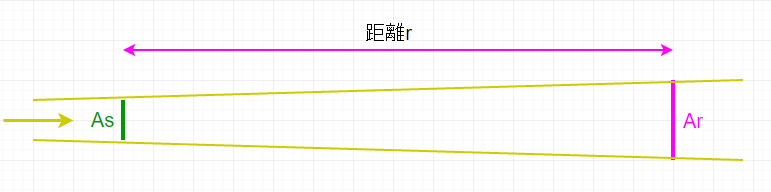
以下のような向かい合う距離がrだけ離れている任意の並行な2つの面を考えます。
そして左から右に光が来ていてAsを通過して同様にArを通過しているシチュエーションだとします。
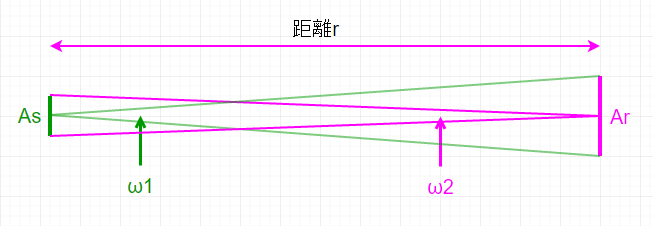
Radiance(放射輝度)をAs, Arで考えたいため、As から Arを見たときの立体角と、ArからAsを見たときの立体角を考えます。(AsもArも十分に小さい場合を想定しています)
それぞれの立体角は、単位球の表面積と、半径rの表面積の関係性を見ると直観的にわかります。
$r^2$で割ってやることで単位球の表面積がわかり、それはまた立体角でもあるわけです。
とすると、ω1は発射する側、ω2はそれを受ける側という立場の違いはありますが、以下のように式を立てることができます。
d \omega_1 = \frac {dA_r}{r^2}\\
d \omega_2 = \frac {dA_s}{r^2}
ここでAsで観測した合計のFlux(放射束)を$\Phi$とします。もちろん同じ量がArにも観測されています。
するとRadiance(放射輝度)はそれぞれ、
L_1 = \frac {d^2 \Phi}{dA_s d\omega_1}\\
L_2 = \frac {d^2 \Phi}{dA_r d\omega_2}
したがって、$\omega_1$, $\omega_2$を代入すると、
L_1 = \frac {d^2 r^2 \Phi}{dA_s dA_r}\\
L_2 = \frac {d^2 r^2 \Phi}{dA_r dA_s}\\
L_1 = L_2 = \frac {d^2 r^2 \Phi}{dA_s dA_r}
なんと、同じ量になりました。
つまりRadiance(放射輝度)はAsで観測しても、Arで観測しても同じなのです。
左側のどこかの光発生源からの距離や考える向きが、AsとArで違うにもかかわらず、です。
Radiance(放射輝度)は距離が変わっても、考える向きが違っても、同じ量を指し示すわけです。
実際のレンダリングではRadiance(放射輝度)をこれでもかというほど活用します。これが便利な理由としては、
・Radiance(放射輝度)を積分することによってあらゆる主要な物理量を導くことが可能であるということ
・距離が変わっても同じ量であることから、幾何学的なレイと相性が良く、一本のレイが運ぶ物理量としては最適
・方向が逆になってもいいということから、視線から追跡するレイトレーシングに矛盾なく取り込める
例えば、カメラの中の特定のセンサーに当たるIrradiance(放射照度)が知りたければ、レンズを通ってそのセンサーに当たるRadiance(放射輝度)を立体角で積分すればいいわけですし、ある表面に当たるIrradiance(放射照度)が知りたければ、全立体角で積分すればいいわけです。
ランバート余弦則
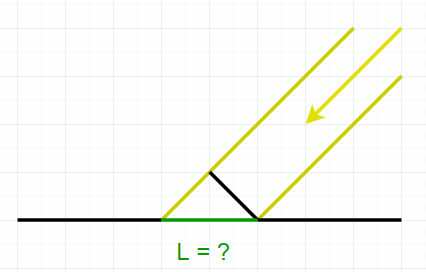
上の定義は、立体角の向きに垂直な面ですべて考えていました。
でも注目している面に斜めに入射するケースを考えたいときはどうなるんでしょうか?
まずは入射方向に垂直な面Aでの放射輝度を考えます。
ここでの放射輝度は定義から以下のように考えられます。
L=\frac { dE }{ d\omega } =\frac { { d }^{ 2 }\Phi }{ d\omega dA }
ここまでは同じですね。
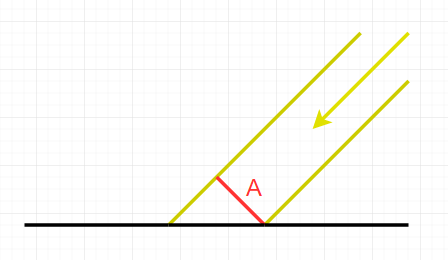
でも実際には下の面にあたっているわけで、これは実際には物理量が引き伸ばされてしまっているわけです。
L=\frac { dE }{ d\omega } =\frac { { d }^{ 2 }\Phi }{ d\omega dA' }
実際2つの面積の関係性は、
\frac { dA' }{ dA } =\cos { \theta } \\ dA'=dA\cos { \theta }
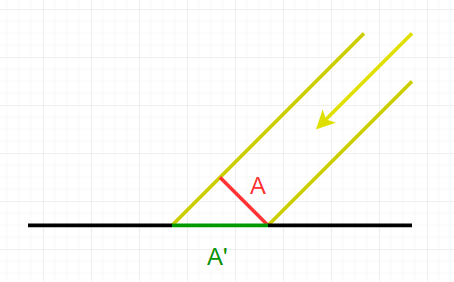
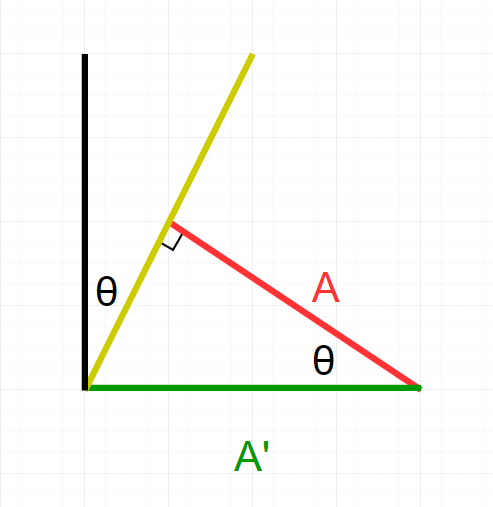
となります。一瞬3Dで考えなければいけないのでは?という疑問もありますが、以下の図のように、
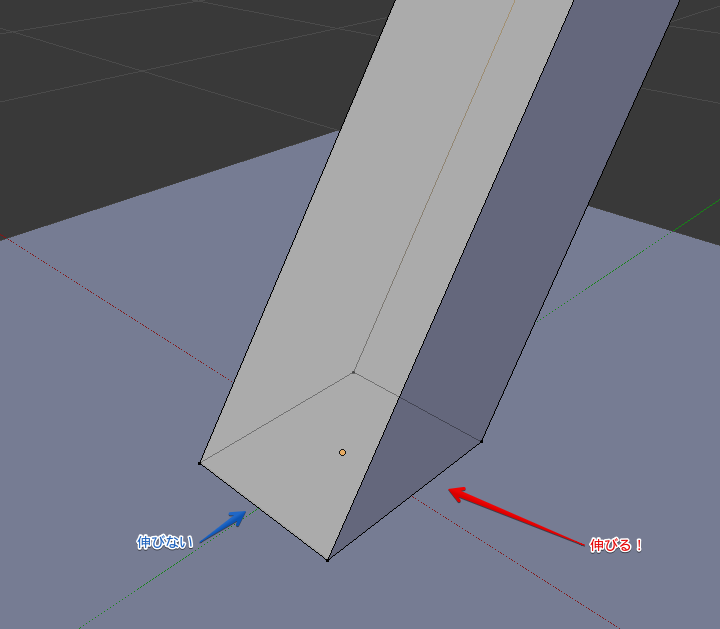
横にしか引き伸ばしが発生していないことがわかります。
というわけで、Radiance(放射輝度)は、
L=\frac { { d }^{ 2 }\Phi }{ d\omega dA' } =\frac { { d }^{ 2 }\Phi }{ d\omega dA\cos { \theta } } \\ L=\frac { { d }I }{ dA\cos { \theta } } \\ L=\frac { { d }E }{ d\omega \cos { \theta } }
というような関係性を見出すことができ、Radiance(放射輝度)を、Irradiance(放射照度)を投影された立体角の微分で考えることができます。
また少し変形して、
{ d }E=L\cos { \theta } d\omega
とすると、ある方向からくる放射輝度がどんなものであっても、面が完全に横を向いている場合は$\cos { \theta }=0$になることから、Irradiance(放射照度)の寄与が0になっていることをよく理解できます。これは直観的にも納得できることでしょう。こう考えると$\cos { \theta }$というのはやや邪魔ではありますが、よくよく辻褄が合うようにできているというわけです。
また、ある点のIrradiance(放射照度)を考える場合は、以下のような積分を適用することが可能です。
E(p)=\int _{ \Omega }^{ }{ L\cos { \theta } d\omega }
完全拡散面
ここまでで、重要な物理量についてはまとめ終わりました。
そこでここらで少し反射について考えてみます。
ある面にある光があたったとき、方向によらずすべての方向に一定の放射輝度を返すような表面を、完全拡散面(Lambertian surface)と呼びます。もちろんそんな理想的な面が現実にあるかどうかは別な話です。
まずは、出ていくRadiance(放射輝度)とRadiant Exitance(放射発散度)(こちらは放射照度の出ていく版でした)の関係性を考えます。これもやはり構造的には先程の放射照度を求めるのと同じで、Radiant Exitance(放射発散度) $M$は、
M=\int _{ \Omega }^{ }{ L\cos { \theta } d\omega }
のように出ていく放射輝度との関係性を表せます。ここでLを定数だとして試しに半球で積分してみましょう。
ここで半球積分は、
\int _{ \Omega }^{ }{ L\cos { \theta } d\omega } =\int _{ 0 }^{ 2\pi }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ L\cos { \theta } \sin { \theta } d\theta d\phi } }
のように極座標での重積分と捉えることができます。
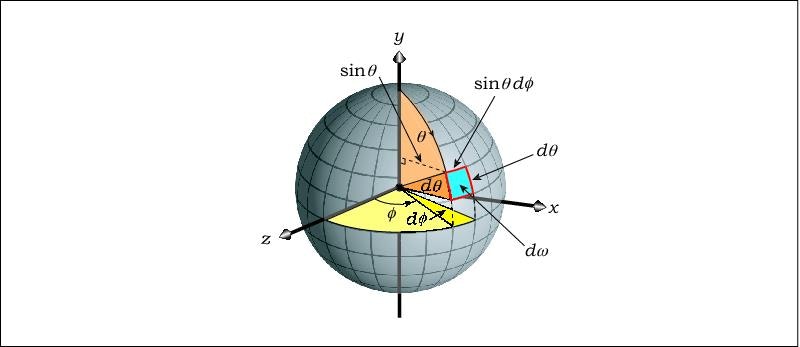
こちらは図形的にはRay Tracing from the Ground Upの図を引用させて頂きます。
式の中の、$\sin { \theta } d\theta d\phi $の部分が丁度$d\omega$に対応する部分です。$\theta$によってxz面での$d\phi$が実際には小さくなり、どのくらい小さくなるか?が$\sin { \theta }$になるためです。
積分が2つ重なっちゃってますが、フビニの定理というやつのおかげで一つ一つ剥がしていけば良いです。
\int _{ 0 }^{ 2\pi }{ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ L\cos { \theta } \sin { \theta } d\theta d\phi } } =\int _{ 0 }^{ 2\pi }{ d\phi } \int _{ 0 }^{ \frac { \pi }{ 2 } }{ L\cos { \theta } \sin { \theta } d\theta } \\ =2\pi \int _{ 0 }^{ \frac { \pi }{ 2 } }{ L\cos { \theta } \sin { \theta } d\theta } \\ =2\pi \int _{ 0 }^{ \frac { \pi }{ 2 } }{ L\frac { 1 }{ 2 } \sin { 2\theta } d\theta } \\ =\pi L\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \sin { 2\theta } d\theta } \\ t=2\theta \\ \frac { dt }{ d\theta } =2\\ \frac { 1 }{ 2 } dt=d\theta \\ =\pi L\int _{ 0 }^{ \pi }{ \sin { t } \frac { 1 }{ 2 } dt } \\ =\pi L\frac { 1 }{ 2 } \left[ -\cos { t } \right] ^{ \pi }_{ 0 }\\ =\pi L\frac { 1 }{ 2 } \{ -\cos { \pi } -\left( -\cos { 0 } \right) \} \\ =\pi L\frac { 1 }{ 2 } \{ 1+1\} \\ M=\pi L
少し長くなってしまいましたが、これで完全拡散面における、Radiant Exitance(放射発散度)と、出射のRadiance(放射輝度)との関係性が見えました。
M=\pi L\\ \frac { 1 }{ \pi } M=L
ここで完全拡散面が受けたIrradiance(放射照度)のうち、いくらかは吸収された後、Radiant Exitance(放射発散度)となるとして、これを、
M=RE
と係数で表現しますと、
L=\frac { R }{ \pi } E
とIrradiance(放射照度)とRadiance(放射輝度)の関係性を見出すことができます。
さらにはIrradiance(放射照度)というのはRadiance(放射輝度)を積分すればよかったわけですから、完全拡散面の表面に到達するRadiance(放射輝度)との関係性まで以下のようにまで見えてきます。
E(p)=\int _{ \Omega }^{ }{ L\cos { \theta } d\omega } \\ L_{ o }=\frac { R }{ \pi } E\\ L_{ o }=\frac { R }{ \pi } \int _{ \Omega }^{ }{ L_{ i }\cos { \theta } d\omega } \\ L_{ o }=\int _{ \Omega }^{ }{ \frac { R }{ \pi } L_{ i }\cos { \theta } d\omega } \\
ここで$\frac { R }{ \pi } $を関数と捉えることができ、定数ではなくもっと複雑な反射モデルを考えることができます。
L_{ o }=\int _{ \Omega }^{ }{ f\left( p,\omega _{ i },\omega _{ o } \right) L_{ i }\cos { \theta } d\omega }
これをBRDF、双方向反射分布関数(Bidirectional Reflectance Distribution Function)と呼びます。
中には物体そのものが光っている場合があります。その場合を考えて、一つ項を増やしますと、
L_{ o }=L_{ e }+\int _{ \Omega }^{ }{ f\left( p,\omega _{ i },\omega _{ o } \right) L_{ i }\cos { \theta } d\omega }
となり、これをレンダリング方程式と呼びます。
まとめ
もっともっと深く掘り下げることもできそうではありますが、ひとまずレンダリング方程式までを繋いでみました。実際見よう見まねでレイトレーシングのコードを書きなぐっていましたが、きちんとした背景があまり今までよくわかっていなかったなぁと勿体なく思います。スタートラインでしかありませんが、まあ誰かの理解にいくらか役に立てればと思います。
参考文献(というかこれを読めばこの記事読まなくてもいいんだよなぁ!)
Physically Based Rendering, Third Edition: From Theory to Implementation
Radiometry Steve Marschner Cornell University
フォトンマッピング―実写に迫るコンピュータグラフィックス
Ray Tracing from the Ground Up
放射輝度 (Radiance) rayspace.xyz