レイトレ合宿アドベントカレンダー5週目の記事です。
https://sites.google.com/site/raytracingcamp5/#TOC--10
もふもふレンダリング入門(1)からの続きになります。
方位角(azimuthal)拡散関数
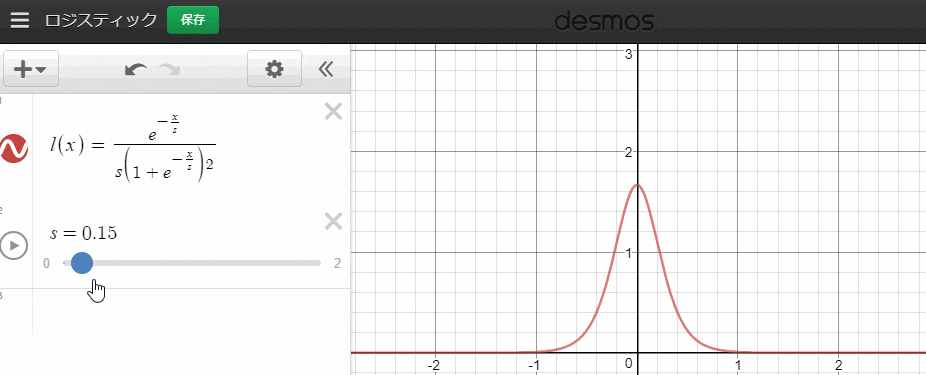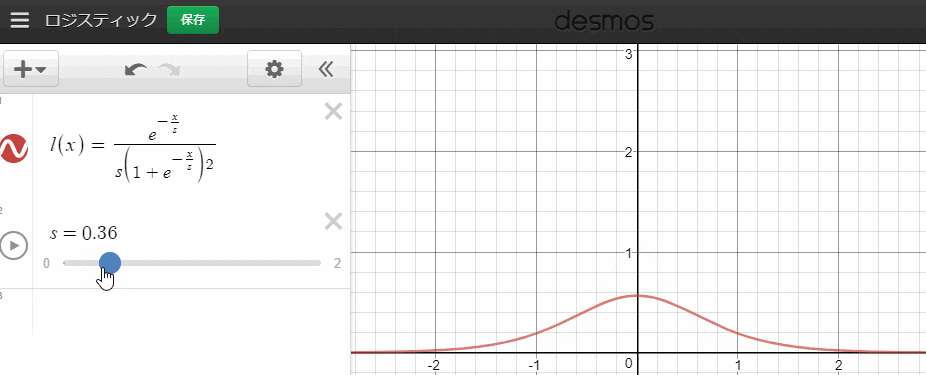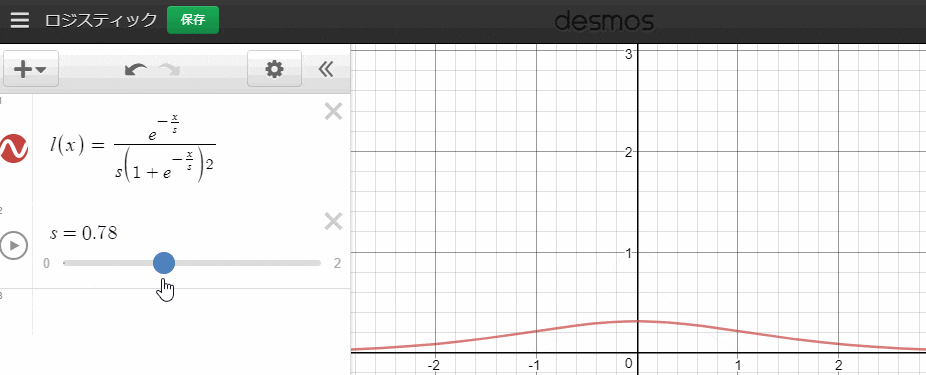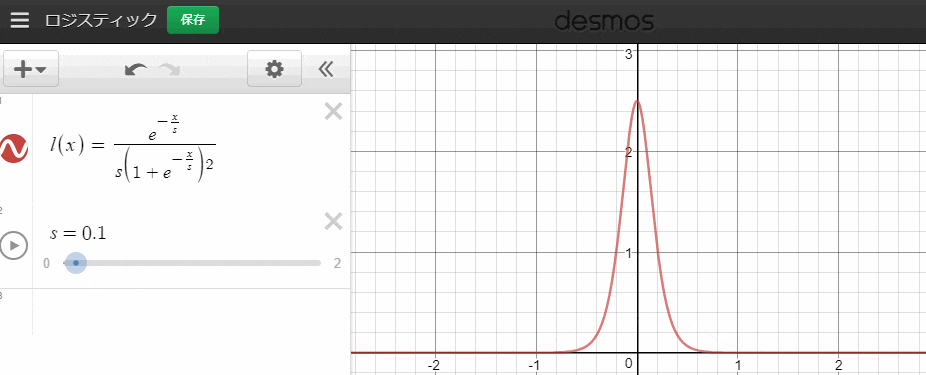
最後の関数です。Mpと似ていますが、方向が違います。ここでは拡散具合をロジスティック分布で表現します。
l\left( x,s \right) =\frac { { e }^{ -\frac { x }{ s } } }{ { s\left( 1+{ e }^{ -\frac { x }{ s } } \right) }^{ 2 } }
実装としては素直に以下のようになります。
inline double Logistic(double x, double s) {
x = std::abs(x);
double exp_minus_x_over_s = std::exp(-x / s);
return exp_minus_x_over_s / (s * Sqr(1.0 + exp_minus_x_over_s));
}
PBRTの実装ではxに絶対値を取っており、これは -x / s が大きな値を取る時の数値的な不安定さを避けるためとのことです。関数は左右対称であるため、数学的には等価です。
なぜロジスティック分布が選ばれているかというと、ガウス分布によく似ていて、解析的な積分が使えること、重点サンプリングが容易であることなどが理由のようです。モデルによってはガウス分布を使う場合もあるようです。
こちらはまた未知のパラメータ $ s $ が登場しますが、これは、Mpと同様に $ \beta_n $ パラメータから変換します。これも直観的な表面の粗さの制御が目的になります。
s=\sqrt { \frac { \pi }{ 8 } } \left( 0.265\beta _{ m }+1.194{ \beta _{ m } }^{ 2 }+5.372{ \beta _{ m } }^{ 22 } \right)
ただこれによってハイライトにダイレクトに影響するわけではないようです。実際レンダリングのサンプルを見てみますと、

[6] Matt Pharr, "01 THE IMPLEMENTATION OF A HAIR SCATTERING MODEL" より
左側の写真のように拡散が弱いほど光が潜り込んでいるようです。一方で拡散が強いほど、周囲へよく光を反射するためか、やや明るく見えます。
さて、このロジスティック分布は統計学でよく知られており、確率密度関数であるため全範囲の積分が常に1になり、解析的な積分は、
\int { l\left( x,s \right) dx } =cdf\left( x,s \right) =\begin{matrix} \int { \frac { e^{ -\frac { x }{ s } } }{ s\left( 1+e^{ -\frac { x }{ s } } \right) ^{ 2 } } dx } \end{matrix}=\begin{matrix} \frac { 1 }{ 1+e^{ -\frac { x }{ s } } } \end{matrix}+C
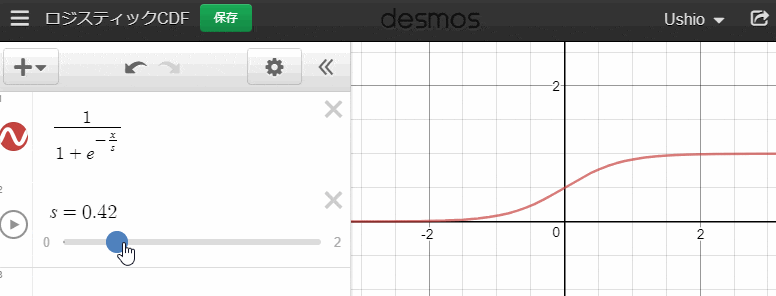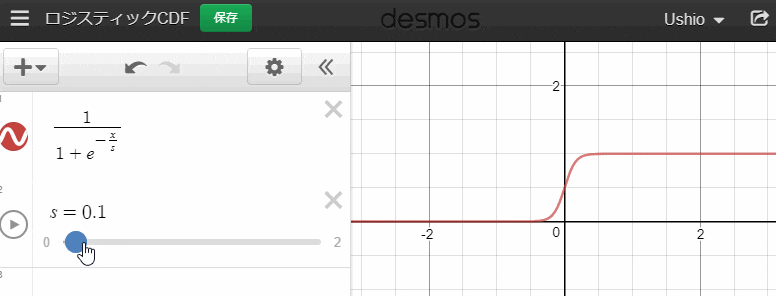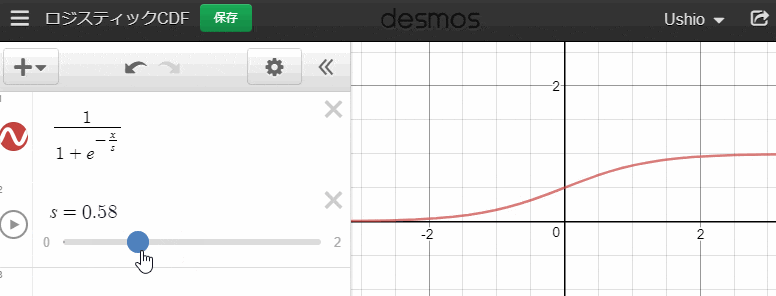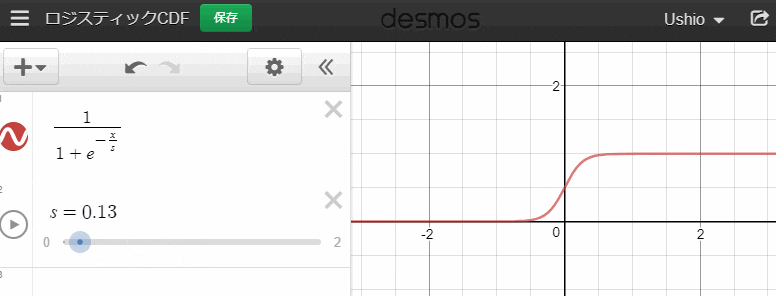
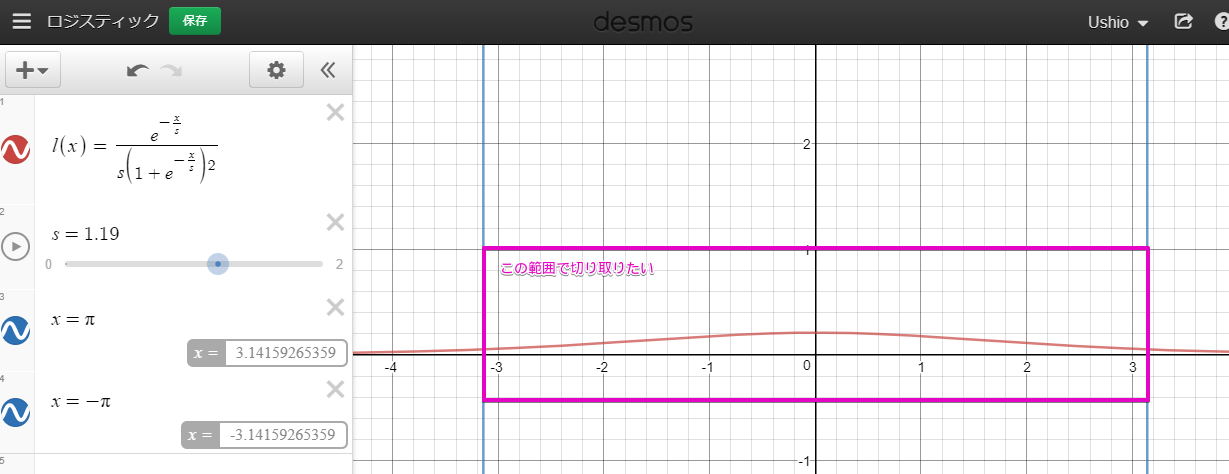
であることが知られています。また、グラフは、
このようになります。
せっかくなので、[8] Attempt to use symbolic computation for renderer verificationで紹介されておりました、sympyで確認してみますと、
>>> from sympy import *
>>> x, s = symbols('x s')
>>> integrate(exp(-x/s) / (s*(1+exp(-x/s))**2), x)
1/(1 + exp(-x/s))
>>>
確かになりました。ついでに全範囲における積分は、
\int _{ \infty }^{ \infty }{ \frac { e^{ -\frac { x }{ s } } }{ s\left( 1+e^{ -\frac { x }{ s } } \right) ^{ 2 } } dx } =\left[ \frac { 1 }{ 1+e^{ -\frac { x }{ s } } } \right] ^{ \infty }_{ -\infty }\\ =\lim _{ x\rightarrow \infty }{ \frac { 1 }{ 1+e^{ -\frac { x }{ s } } } } -\lim _{ x\rightarrow -\infty }{ \frac { 1 }{ 1+e^{ -\frac { x }{ s } } } } \\ =\frac { 1 }{ 1+0 } -0\\ =1
と確かに1になることも確認できます。
実装のほうは素直に、
inline double LogisticCDF(double x, double s) {
return 1.0 / (1.0 + std::exp(-x / s));
}
となりました。
しかし残念ながらこのまま使うには、関数の範囲が無限であるという点が使いにくいです。方位角(azimuthal)はやはり $ -\pi $ から $ \pi $ の範囲の世界であるため、それに合わせ関数を"切り取る"ことを考えます。
ただ切り取った後も[-π ~ π]の積分をやはり1にしておきたいため、カットした分を補正した関数は以下のようになります。
l_{ trim }\left( x,s,[a,b] \right) =\frac { l\left( x,s \right) }{ \int _{ a }^{ b }{ l\left( z,s \right) dz } }
つまるところ、切り取った範囲の積分値が例えば0.8なら、$ \frac{1}{0.8} $ 倍すれば1になるということですね。定積分なので、
l_{ trim }\left( x,s,[a,b] \right) =\frac { l\left( x,s \right) }{ \int _{ a }^{ b }{ l\left( z,s \right) dz } } =\frac { l\left( x,s \right) }{ \left[ cdf\left( x \right) \right] ^{ b }_{ a } } =\frac { l\left( x,s \right) }{ cdf\left( b \right) -cdf\left( a \right) }
となりますので、実装は、
inline double TrimmedLogistic(double x, double s, double a, double b) {
return Logistic(x, s) / (LogisticCDF(b, s) - LogisticCDF(a, s));
}
となります。(ただPBRTの実装では結局 $ a=-\pi, b=\pi $ がハードコードされています)
これでひとまず中核となる関数はできました。0位置が寄与のピークであるこの関数をピーク角度からの角度差を引数にとり、寄与を返す関数と捉えることにしましょう。
しかし実際には方位角(azimuthal)拡散関数は、各段階(p)での光線追跡角度に依存する形になります。これはコルテックス層(Cortex), メデュラ層(Medulla)で光が屈折するからです。
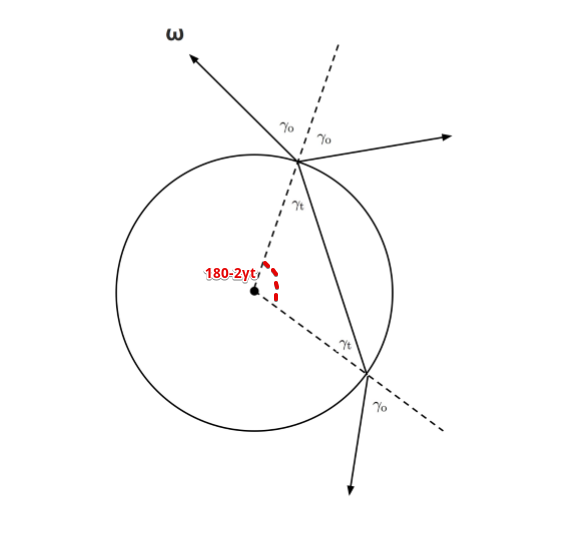
図で考えると、
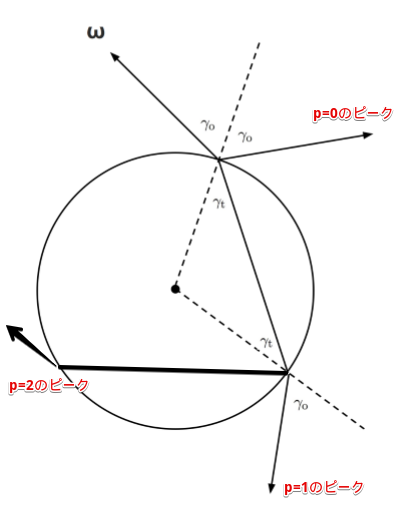
[6] Matt Pharr, "01 THE IMPLEMENTATION OF A HAIR SCATTERING MODEL"にちょっと付け足したもの
今回の座標系ではマイナス角度方向が時計回りであることに注意しつつつ、
p=0のとき
-2\gamma _{ o }
真ん中の角度が $ \pi - 2 \gamma_t $ であるので、
p=1のとき
-2\gamma _{ o }-\left( \pi -2\gamma _{ t } \right)
ところで考えてみると、結局これに続く反射はp=0からp=1に行くときと全く同じ話であることに気づきます。
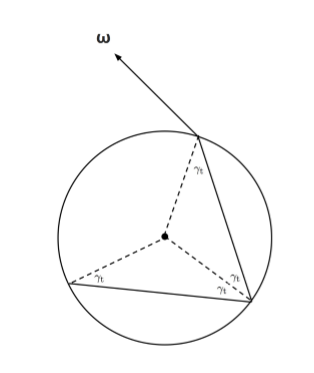
したがって、結局ある段階(p)における、$ \omega_o $ を初期角度0と基準にしたときの、ピーク角度は、
-2\gamma _{ o }-p\left( \pi -2\gamma_{ t } \right) =-2\gamma _{ o }-p\gamma_{ t }-p\pi
と一般化することができます。
inline double Phi(int p, double gammaO, double gammaT) {
return 2.0 * p * gammaT - 2.0 * gammaO + p * glm::pi<double>();
}
ちなみに $ \gamma_{ t } , \gamma _{ o } $ については以下のように求めます。$ h=\sin { \gamma } $ であることを思い出します。
double gammaT = SafeASin(sinGammaT);
double gammaO = SafeASin(h);
実際の方位角(azimuthal)拡散関数Npでは便宜的に、$ \omega_o $ を0基準とした $ \omega_i $ までの相対的な角度差を引数にとることにします。
double phiO = std::atan2(wo.z, wo.y);
double phiI = std::atan2(wi.z, wi.y);
double phi = phiI - phiO;
for (int p = 0; p < 3; ++p) {
Np(phi, p, s, gammaO, gammaT);
}
※上は擬似コード
Np本体では、pを元にピークの相対角度を算出し、実際の角度とどれだけ差があるか計算します。
inline double Np(double phi, int p, double s, double gammaO, double gammaT) {
double dphi = phi - Phi(p, gammaO, gammaT);
その差を、先程準備したTrimmedLogistic関数に渡せば、評価は完了です。
ただ $ \left[-\pi, \pi \right] $ をはみ出るのは嫌なので、そこだけハンドリングしてやれば、
inline double Np(double phi, int p, double s, double gammaO, double gammaT) {
double dphi = phi - Phi(p, gammaO, gammaT);
while (dphi > glm::pi<double>()) dphi -= 2.0 * glm::pi<double>();
while (dphi < -glm::pi<double>()) dphi += 2.0 * glm::pi<double>();
return TrimmedLogistic(dphi, s, -glm::pi<double>(), glm::pi<double>());
}
という実装になります。
BSDF
主要な関数はすべて揃いました。なのでそろそろ本体の関数の実装に移りましょう。もう一度レンダリング方程式と、BSDFの中身を思い出しますと、
L_{ o }=\int _{ { S }^{ 2 } }^{ }{ \sum _{ p=0 }^{ \infty }{ \frac { M_{ p }\left( \theta _{ o },\theta _{ i } \right) A_{ p }\left( \theta _{ o } \right) N_{ p }\left( \phi \right) }{ |\cos { \theta _{ i } } | } } L_{ i }\left| \cos { \theta } \right| d\omega _{ i } }
f_{ p }\left( \omega _{ i },\omega _{ o } \right) =\frac { M_{ p }\left( \theta _{ o },\theta _{ i } \right) A_{ p }\left( \theta _{ o } \right) N_{ p }\left( \phi \right) }{ |\cos { \theta _{ i } } | }
となっています。ただ実際に真面目に評価するのはp=0,1,2,3までとなり、p=3については残りすべてを内包していることにします。
ところでまだ使っていないパラメータ $ \alpha $ がありました。これはキューティクル層(Cuticle)層の起き上がりであり、経度(longitudinal)角度にのみ影響します。
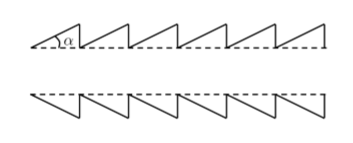
ただ、pによってどれだけ補正するかは違います。なぜかというと、p=0では反射、p=1では屈折->屈折、p=2では屈折->反射->屈折と表面を通過する経路が違うからです。
まとめると以下のように段階ごとに補正する量を変える必要があります。
| p | 回転 |
|---|---|
| 0 | $ 2\alpha $ |
| 1 | $ -\alpha $ |
| 2 | $ -4\alpha $ |
| 3 | $0$ |
このオフセットにより、以下のような差が生まれるそうです。うーん、右のほうがリアル・・・なんでしょうか?

[6] Matt Pharr, "01 THE IMPLEMENTATION OF A HAIR SCATTERING MODEL" より
実際の補正処理には、加法定理を使います。
\sin { \left( \theta \pm \alpha \right) } =\sin { \theta } \cos { \alpha } \pm \cos { \theta } \sin { \alpha } \\ \cos { \left( \theta \pm \alpha \right) } =\cos { \theta } \cos { \alpha } \mp \sin { \theta } \sin { \alpha }
したがって実際に使う式は、
p=0\\ \sin { \left( \theta +2\alpha \right) } =\sin { \theta } \cos { 2\alpha } +\cos { \theta } \sin { 2\alpha } \\ \cos { \left( \theta +2\alpha \right) } =\cos { \theta } \cos { 2\alpha } -\sin { \theta } \sin { 2\alpha }
p=1\\ \sin { \left( \theta -\alpha \right) } =\sin { \theta } \cos { \alpha } -\cos { \theta } \sin { \alpha } \\ \cos { \left( \theta -\alpha \right) } =\cos { \theta } \cos { \alpha } +\sin { \theta } \sin { \alpha }
p=2\\ \sin { \left( \theta -4\alpha \right) } =\sin { \theta } \cos { 4\alpha } -\cos { \theta } \sin { 4\alpha } \\ \cos { \left( \theta -4\alpha \right) } =\cos { \theta } \cos { 4\alpha } +\sin { \theta } \sin { 4\alpha }
となりますが、$ \cos { { 2 }^{ k }\alpha } ,\sin { { 2 }^{ k }\alpha } $ については、2倍角の公式により先に求めてしまいます。
\sin { 2\alpha } =2\sin { \alpha } \cos { \alpha } \\ \cos { 2\alpha } =\cos ^{ 2 }{ \alpha } -\sin ^{ 2 }{ \alpha }
1回計算すると $ \alpha $ が二倍になることをうまく利用しています。
std::array<double, 3> sin2kAlpha;
std::array<double, 3> cos2kAlpha;
sin2kAlpha[0] = std::sin(alpha);
cos2kAlpha[0] = SafeSqrt(1 - Sqr(sin2kAlpha[0]));
for (int i = 1; i < 3; ++i) {
sin2kAlpha[i] = 2 * cos2kAlpha[i - 1] * sin2kAlpha[i - 1];
cos2kAlpha[i] = Sqr(cos2kAlpha[i - 1]) - Sqr(sin2kAlpha[i - 1]);
}
これを使ってあとは素直に加法定理を適用すれば完了です。
以上をふまえて、一気に全貌を出しますと、
inline glm::dvec3 bsdf(glm::dvec3 wi, glm::dvec3 wo, double h) {
// パラメータはひとまずハードコーディング
double eta = 1.55;
double beta_n = 0.9;
double beta_m = 0.9;
double alpha = 0.000;
Vec3 sigma_a(0.0);
double sinThetaO = wo.x;
double cosThetaO = SafeSqrt(1.0 - Sqr(sinThetaO));
double phiO = std::atan2(wo.z, wo.y);
double sinThetaI = wi.x;
double cosThetaI = SafeSqrt(1.0 - Sqr(sinThetaI));
double phiI = std::atan2(wi.z, wi.y);
double s = beta_n_to_s(beta_n);
double sinThetaT = sinThetaO / eta;
double cosThetaT = SafeSqrt(1.0 - Sqr(sinThetaT));
double etap = glm::sqrt(eta * eta - Sqr(sinThetaO)) / cosThetaO;
double sinGammaT = h / etap;
double cosGammaT = SafeSqrt(1 - Sqr(sinGammaT));
double gammaT = SafeASin(sinGammaT);
double l = 2.0 * cosGammaT / cosThetaT;
Vec3 T = glm::exp(-sigma_a * l);
std::array<double, 3> sin2kAlpha;
std::array<double, 3> cos2kAlpha;
sin2kAlpha[0] = std::sin(alpha);
cos2kAlpha[0] = SafeSqrt(1 - Sqr(sin2kAlpha[0]));
for (int i = 1; i < 3; ++i) {
sin2kAlpha[i] = 2 * cos2kAlpha[i - 1] * sin2kAlpha[i - 1];
cos2kAlpha[i] = Sqr(cos2kAlpha[i - 1]) - Sqr(sin2kAlpha[i - 1]);
}
double gammaO = SafeASin(h);
double phi = phiI - phiO;
std::array<Vec3, pMax + 1> ap = Ap(cosThetaO, eta, h, T);
std::array<double, pMax + 1> v = betam_to_v(beta_m);
Vec3 fsum(0.);
for (int p = 0; p < 3; ++p) {
double sinThetaIp, cosThetaIp;
if (p == 0) {
sinThetaIp = sinThetaI * cos2kAlpha[1] + cosThetaI * sin2kAlpha[1];
cosThetaIp = cosThetaI * cos2kAlpha[1] - sinThetaI * sin2kAlpha[1];
}
else if (p == 1) {
sinThetaIp = sinThetaI * cos2kAlpha[0] - cosThetaI * sin2kAlpha[0];
cosThetaIp = cosThetaI * cos2kAlpha[0] + sinThetaI * sin2kAlpha[0];
}
else if (p == 2) {
sinThetaIp = sinThetaI * cos2kAlpha[2] - cosThetaI * sin2kAlpha[2];
cosThetaIp = cosThetaI * cos2kAlpha[2] + sinThetaI * sin2kAlpha[2];
}
else {
sinThetaIp = sinThetaI;
cosThetaIp = cosThetaI;
}
cosThetaIp = std::abs(cosThetaIp);
fsum += Mp(sinThetaIp, cosThetaIp, sinThetaO, cosThetaO, v[p]) * ap[p] * Np(phi, p, s, gammaO, gammaT);
}
// もうちょっと続く
}
cosThetaIpは、微妙に負の値を取ることもあり、一応絶対値を取っているところがあります。
そしてp=3の部分です。
fsum += Mp(cosThetaI, cosThetaO, sinThetaI, sinThetaO, v[pMax]) * ap[pMax] / (2.0 * glm::pi<double>());
ここではp=3以降の部分ですね、ただしNpに関しては均一分布である、
N\left( \phi \right) =\frac { 1 }{ 2\pi }
を使うそうです。高次の項においては、寄与がそれほど高くなく、複雑な多重反射の後に出てくるのでもはやざっくり均一にしてしまおうということでしょう。
if (AbsCosTheta(wi) > 0) {
fsum /= AbsCosTheta(wi);
}
最後に忘れずにcosの部分です。ここ実は注意が必要で、PBRTの実装においては、
inline float AbsCosTheta(const Vector &w) { return fabsf(w.z); }
となっています。ただよくよく考えると今回のケースでは法線の考え方が違うためこれは不適切で、
inline double AbsCosThetaForHair(const Vec3 &w) {
return glm::sqrt(w.z * w.z + w.y * w.y);
}
が妥当ではないかと思ました。しかししかし、よくよく考えるとこの項というのはレンダリング方程式における、cos項をキャンセルするためのものであるため、PBRTの枠組みにおいてはAbsCosThetaを使わざるを得なかったのではと思われます。
なので、自身のレンダリングシステムの中に組み込む時には、cos項の扱いには一つ注意が必要かもしれません。
以上でBSDF本体の実装は完了です。
以下が今までの関数をすべて含むソースコードになります。(ただし、ほとんどPBRTのコードの写経になります。悲しい・・・。)
https://gist.github.com/Ushio/c14aa8e023de842e20fc436d265bce7e
テスト
簡単ではありますが、テストを書きます。今回のBSDFは、$ \sigma_a = 0, \alpha = 0 $ であれば、綺麗にエネルギー保存を守ってくれます。したがって、
\int _{ { S }^{ 2 } }^{ }{ f\left( \omega _{ i },\omega _{ o } \right) \left| \cos { \theta } \right| d\omega _{ i } } = 1
を満たしてくれるはずです。なので一様サンプリングのモンテカルロ推定器を使い、
\frac { 1 }{ n } \sum _{ i=0 }^{ n }{ \frac { f\left( \omega _{ i },\omega _{ o } \right) \left| \cos { \theta } \right| }{ p\left( \omega _{ i } \right) } } = 1
であるかをテストします。ただし、全球で一様サンプリングなので確率密度関数は球の立体角である、
p\left( \omega _{ i } \right) =\frac { 1 }{ 4\pi }
です。ただ、hについては少し乱暴ですがランダムに決めてしまいます。乱暴といっても、hは主に屈折に関わる部分に影響はしますが、エネルギー保存にはなんら影響がありませんので、問題無いといえます。
for (int j = 0; j < 10; ++j) {
Vec3 wo = uniform_on_unit_sphere(&random);
Vec3 sum;
int count = 300000;
for (int i = 0; i < count; ++i) {
double h = -1.0 + 2.0 * random.uniform();
Vec3 sigma_a;
Vec3 wi = uniform_on_unit_sphere(&random);
sum += rt::bsdf(wi, wo, h) * rt::AbsCosThetaForHair(wi);
}
double p = 1.0 / (4.0 * glm::pi<double>());
double avg = sum.y / (count * p);
if (avg >= .95 && avg <= 1.05) {
printf("ok %f\n", avg);
}
else {
printf("failed... %f\n", avg);
}
}
このテストも完璧ではまったくないですが、無いよりは遥かにいいでしょう。
重点サンプリング, 衝突判定
重要度サンプリングは効率的なレンダリングではとても大切な話題です。特にハイライトが発生するようなローブが急なパラメータ設定の場合には必須とも言えます。しかし・・・ちょっと力尽きてしまったので、また別記事にさせてください。
また、BSDFができただけでは残念ながらレンダリングまでは至りません。最低限直線や、もしくは多項式曲線と光線の効率的な衝突判定ができて初めてレンダリングが可能になります。しかしこれもなかなか大きなトピックです。これも今後の課題とさせてください。
基本は、
[9] Koji Nakamaru, Yoshio Ohno, "RAY TRACING FOR CURVES PRIMITIVE"
や、
[10] Sven Woop, Carsten Benthin, Ingo Wald, Gregory S. Johnson, and Eric Tabellion, "Exploiting Local Orientation Similarity for Efficient Ray Traversal of Hair and Fur"
あたりを参考にするのが良さそうです。
自分のテストレンダリングにおいては、あまり凝った作りではないOBBツリーを用いましたが、これがなかなか重い・・・。このあたりも工夫の余地が大いにあるでしょう。
まとめ & ポエム
大変わかりやすい解説である、Matt Pharr, "01 THE IMPLEMENTATION OF A HAIR SCATTERING MODEL"を参考に進めて参りましたが、まだ細かいところであれ?これなんでだろう?と思うところもちらほらありました。しかもたくさんの論文の上に成り立っているため、その理論的背景は複雑で高度です。実装だけでも緻密な工夫が要求され、正直なところ圧倒されてしまいました。。。
しかしながら、見よう見まねのあっても多く学ぶことのできる箇所は存在し、多くの気づきを得ることができました。強い方々は、もうそんなの当然やろ!みたいなところも数多くあったかもしれませんが、このまとめを通じていくらかでも新しい何かに気づけるきっかけになればと思います。
レンダリング
レイトレ合宿5‽にて提出致しました、MofuMofuRender によるレンダリングです!
参考文献
[6] Matt Pharr, "01 THE IMPLEMENTATION OF A HAIR SCATTERING MODEL"
[8] lightmetrica.org, "Attempt to use symbolic computation for renderer verification"
[9] Koji Nakamaru, Yoshio Ohno, "RAY TRACING FOR CURVES PRIMITIVE"
もふもふレンダリング入門(3)
レイトレ合宿5‽のセミナーにて続編を発表させて頂きました!
宿題だった重点サンプリングなどの話題がカバーされております。
https://speakerdeck.com/ushiostarfish/mohumohurendaringuru-men-3