レイトレ合宿アドベントカレンダー5週目の記事です。
https://sites.google.com/site/raytracingcamp5/#TOC--10
はじめに

An Efficient and Practical Near and Far Field Fur Reflectance Model [1] より
いやー最高にもふもふですね、
というわけで、自分のレンダラでももふもふレンダリングをトライしてみたくなりました。~~昨今のけものフレンズブームもあり、もふもふレンダリングへの需要が高まっています。~~どうやらコンピュータグラフィックスにおいてもたくさんの先行研究があるようです。
髪(hair)と毛皮(fur)のレンダリング手法色々
まず毛のレンダリング手法にはどんなものがあるのか?というのをざっと見てみることにします。
Kajiya-Kayモデル [2], [3]
異方性鏡面反射成分と拡散成分の組み合わせに基づいた最初の物理的ベースの反射率モデルです。手軽にいわゆる"天使の輪"を出すことができるため、リアルタイム向けにも結構使われてきたようです。ただ毛皮のレンダリングにはあまり向いていません。
Marschener モデル [4]
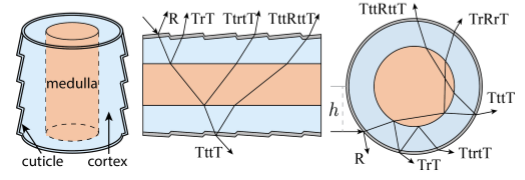
Kajiya-Key モデルをさらに進めて、円筒でモデル化を行い、内部での複数段階の反射も考慮に入れるようになりました。さらに反射の方向を、以下の図のθおよびΦに分離し、各段階をその関数の積としてモデル化しました。このアイディアは後のHair&Furの物理ベースシェーディングの研究に大きな影響を与えています。こちらも人間の髪の毛を主眼をにおいています。
An Empirical Fur Shader [5]
あらかじめ微小な毛の構造から拡散関数をunicube map(いわゆる6面のキューブマップ)として事前計算し、それを元にレンダリングを行う手法です。微小な毛の構造は、MayaのようなDDCツールを使って作ったり、プロシージャル的に生成する方法があります。この枠組では、人間の髪と、動物の毛皮、共に表現が可能であるのも強みです。逆に問題点としては、毛の構造と実際にレンダリングされる絵に乖離があることだと結論で言及されています。
A Practical and Controllable Hair and Fur Model for Production Path Tracing [7]
ここでは、髪や毛皮のレンダリングにおいて主流になっている手法をベースに、プロダクションユースを前提においたシェーディングの計算量を大きく減らすための定式化や、直観的なユーザーコントロールのためのパラメータ化、重点サンプリングのための工夫などが盛り込まれています。
An Efficient and Practical Near and Far Field Fur Reflectance Model [1]
siggraph 2017でも、単体というより続きものであります。実際の計測に基づき、性質の違う2重の円筒でのモデル化による非常にリアリスティックかつ効率的なレンダリング方法、および近距離場・遠距離場レンダリングの統合方法を提案しています。余談ですが、自分がファーレンダリングをやってみたいと思ったきっかけは、このハムスターだったりします。
実装せよ
さて、ではどういうのから実装をチャレンジしたものかというところですが、新しめの論文はどれも難しく、なかなか自分の実力不足でどこをどう実装していけばいいのか困ってしまいました。
何か参考になるものはと調べた所、
"Physically-Accurate Fur Reflectance: Modeling, Measurement and Rendering"の実装報告
というのも見つけて課金してみましたが、とても参考にはなったのですが、残念ながら実装の詳細まではあまり触れられてはいませんでした。といっても髪と毛皮のレンダリングをやってみたい人にとっては貴重資料ですので、是非興味ある方は課金してみることをおすすめします。
もうちょっと探してみると、なんとPBRTに詳しい実装の解説PDF 01 THE IMPLEMENTATION OF A HAIR SCATTERING MODELがあるではありませんか!
ここはありがたく、これに沿って進めてみようと思います。この解説では、"A Practical and Controllable Hair and Fur Model for Production Path Tracing" をベースにしているとのことで、いい感じに新しめの手法であるのも嬉しいところです。では一つ一つ見ていくことにしましょう。
レンダリング方程式
レイトレーシングにおける放射輝度って結局何なのか?でも紹介しました、レンダリング方程式ですが、やはり今回の髪や毛皮のレンダリングにおいても、この方程式からそう大きく外れません。
L_{ o }=L_{ e }+\int _{ \Omega }^{ }{ f\left( \omega _{ i },\omega _{ o } \right) L_{ i }\cos { \theta } d\omega }
先の記事では積分範囲がまるで半球が前提のような記述をしてしまいましたが、現実問題必ずしもそれで表現できる材質ばかりではありません。今回の例でいうと、毛は反対側からの光を透過&吸収&拡散を起こすため、半球の範囲で光が輸送されると仮定するのには無理があります。そこで、範囲を半球から全球へと拡張することにします。また、毛は発光しないとすると概念的な式は、
L_{ o }=\int _{ { S }^{ 2 } }^{ }{ f\left( \omega _{ i },\omega _{ o } \right) L_{ i }\left| \cos { \theta } \right| d\omega _{ i } }
のようになります。このように反射だけでなく、透過&拡散を考えた関数をBRDFと区別し、BSDF (Bidirectional Scatter distribution function) と呼びます。髪や毛皮のレンダリングにおいては、このBSDFをいかに物理的により正確かつ効率的に計算するかというのが、一つの大きな焦点になっています。ただ、一応注意したい点として今回BSDFを考えるのは、髪や毛皮はBSDFで表現できるという意味ではなく、髪や毛皮はBSDFで表現できると仮定して話を進めると一応確認しておきます(この場合というより、数式で自然現象を説明するときは大体こうなる気がしますが・・・)。これはレンダリング時に毛の太さがピクセルよりも十分に細く、内部での複雑な拡散の挙動は無視できる、割に合わないといってもいいでしょう。というわけで、このBSDFをいかに実装するのかが今回の目標となります。
物理的な構造
マイクロファセットBRDFでもそうですが、今回も材質の微小な構造をヒントにBSDFを考えていきます。髪や毛皮の光輸送を考えるうえで大事な物理構造は以下の要素があります。
- キューティクル層(Cuticle)
- コルテックス層(Cortex)
- メデュラ層(Medulla)
[1] "An Efficient and Practical Near and Far Field Fur Reflectance Model" より
**キューティクル層(Cuticle)**は、毛の表面です。粗さをもっていて、表面にわずかに傾きがあります。
**コルテックス層(Cortex)**は、光を波長別に吸収する層です。髪の毛においてはこれが体積の90%を占めるらしいですが、毛皮についてはこの部分の割合が少ないそうです。
**メデュラ層(Medulla)**は、中心部であり、光の吸収・拡散を引き起こします。Marschenerモデルではこの層は無視されており、それが毛皮のレンダリングに適さない大きな理由となっていました。
ただ、今回のモデルでは、髪内部の光散乱を吸収するだけの均質な媒質と仮定するようです。また、図では各層で光の屈折を考慮にいれていますが、コルテックス層(Cortex)とメデュラ層(Medulla)の屈折率を同じものとし、光学現象の簡略化を行っています。
こう見ると先のBSDFの仮定がかなり大胆な気もしてきますが、気にせず進みましょう。
これらの物理的側面を関数として落とし込んでいくことになります。
座標系
そろそろこのBSDFでの取り扱う座標系の整理をしておきます。
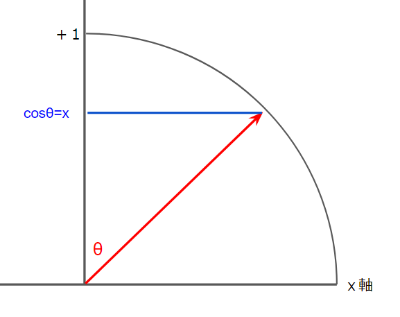
次に $ \theta, \phi $ の2変数により定義できる極座標系を考えます。
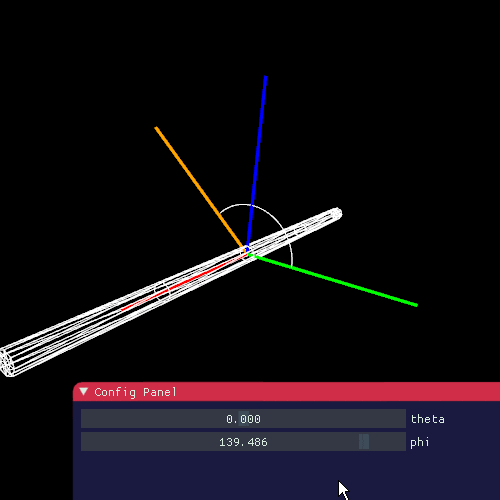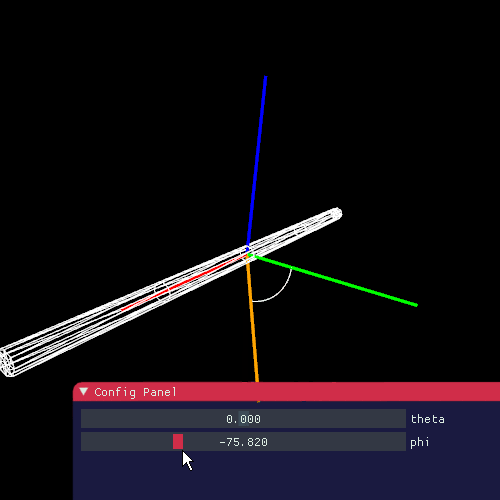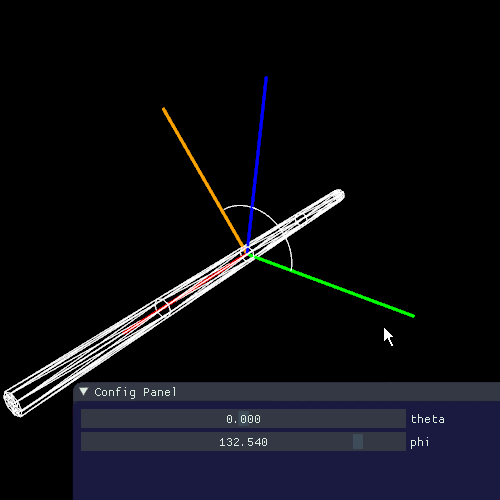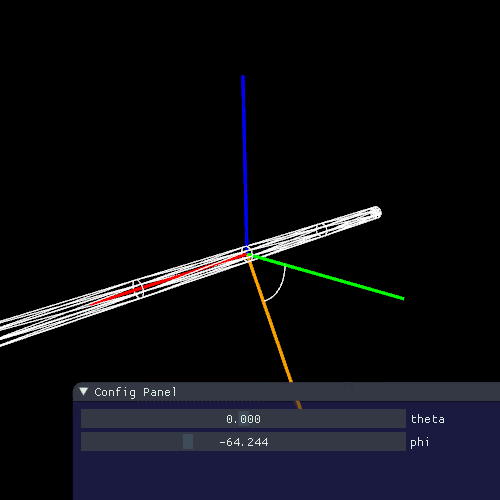
下の図のように経度(longitudinal) を $ \theta $ をとります。先のレンダリング方程式の $ \theta $ もこれになります。
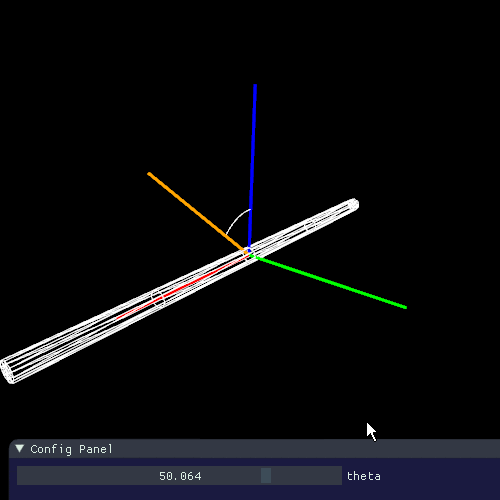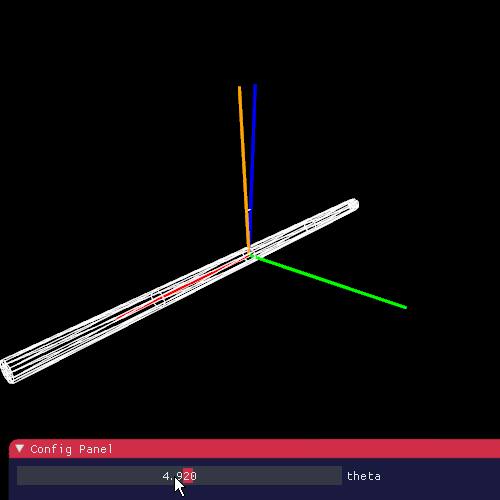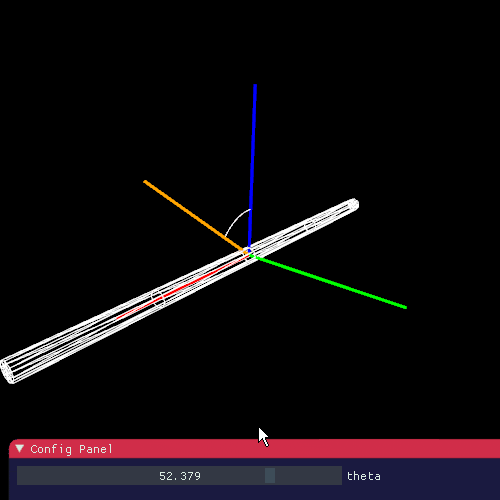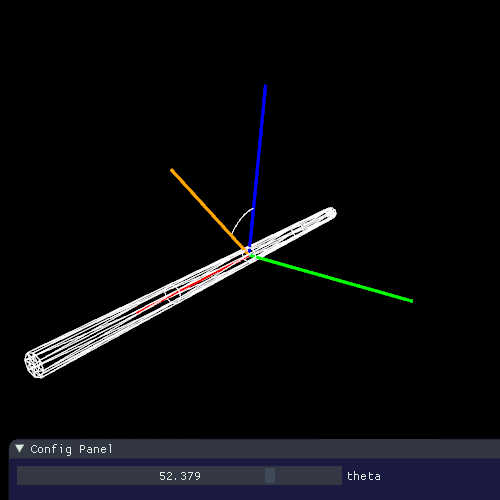
経度は法線との角度と捉えることができますが、毛の接線に垂直である法線は1回転分無数に存在しており、面を生成します。そのため経度はこの面とのなす角度ということになります。(見やすさのためにz軸から伸ばしています)
下の図のように**方位角(azimuthal)**を $ \phi $ ととります。ここではy軸を基準に角度を定めます。
いつの間にかあれどっちだっけ?といらぬ混乱を避けるために、図をしっかりと整理しておきます。
実際のレイトレーシングで使う場面では、本計算に入る前にこのローカルな座標系への変換を前処理として行うことになります。
BSDFの中身
先の物理的な構造の図をもう一度見てみますと、
[1] "An Efficient and Practical Near and Far Field Fur Reflectance Model" より
毛の内部では反射・拡散・吸収が多段階にわたってたくさん起こることがわかります。つまり最終的にある方向への光の量というのは、各段階での寄与の和で表すことができそうです。このため、今回のBSDFもこの物理的側面を尊重し、多段階の光輸送の性質を表現した実装になります。
式としては、pがそれぞれの段階を表すとして、以下のように表現されます。
f\left( \omega _{ i },\omega _{ o } \right) =\sum _{ p=0 }^{ \infty }{ f_{ p }\left( \omega _{ i },\omega _{ o } \right) }
図で同時に確認しておきます。
[6] Matt Pharr, "01 THE IMPLEMENTATION OF A HAIR SCATTERING MODEL" より
R, T の記号は、Rは反射で、Tが透過を表しています。
さらにこの $ f_{ p } $ は、各段階における 経度(longitudinal)拡散関数 $ M_p $ 、吸収関数 $ A_p $ 、方位角(azimuthal)拡散関数 $ N_p $ で表し、各段階をその積であるとします。先の物理的性質を表現しようとしている意図が見て取れます。
f_{ p }\left( \omega _{ i },\omega _{ o } \right) =\frac { M_{ p }\left( \theta _{ o },\theta _{ i } \right) A_{ p }\left( \theta _{ o } \right) N_{ p }\left( \phi \right) }{ |\cos { \theta _{ i }| } }
全部書くと全体像は、
L_{ o }=\int _{ { S }^{ 2 } }^{ }{ \sum _{ p=0 }^{ \infty }{ \frac { M_{ p }\left( \theta _{ o },\theta _{ i } \right) A_{ p }\left( \theta _{ o } \right) N_{ p }\left( \phi \right) }{ |\cos { \theta _{ i } } | } } L_{ i }\left| \cos { \theta } \right| d\omega _{ i } }
となります。
ただ、実際無限の段階を評価することは難しく、今回のBSDFにおいては、p=0~2の部分を真面目に計算し、p=3の部分で残りの高次の項を表現したことにする、という立場をとります。これは、PBRTにおいては、static const int pMax = 3; としてハードコードされています。
BSDFのパラメータ
例えばCook-Torranceにroughnessのパラメータがあるように、このBSDFでもいくつかのパラメータにより質感を定義できるようになっています(先の数式では省略されていましたが)。それらをひとつづつ見てみましょう。
$ \eta $
コルテックス層(Cortex), およびメデュラ層(Medulla)の屈折率です。通常は1.55を使用します。先に述べた通り、今回はコルテックス層(Cortex)とメデュラ層(Medulla)で屈折率は同じものとして扱います。
$ \sigma_a $
毛の内部の吸収係数です。髪や毛の色を決めるのもこのパラメータです。"吸収"係数なので、そのまま色になるわけではなく、CMYKのような減法混色の考え方をすることに注意しましょう。直観的な指定方法もあるようですが、この記事では省略します。各スペクトルごとの係数になります(例えばRGBなら3成分)。 BSDFの評価時には、毛の中を進んだ距離に応じて吸収具合が変化します。距離は後述するhなどにより算出します。
$ \beta_m $
毛の経度(longitudinal)の粗さを決めるパラメータです。範囲 0~1 で直観的な指定ができるように工夫がなされています。1に近づくほど表面がざらざらしていることを表し、全方向に均一に光を拡散します。逆に0に近いほど鏡面反射が強くなり、つやつやした見た目になります。
$ \beta_n $
毛の方位角(azimuthal)の粗さを決めるパラメータです。 範囲 0~1 で直観的な指定ができるように工夫がなされています。1に近づくほど表面がざらざらしていることを表し、全方位に均一に光を拡散します。逆に0に近いほど鏡面反射が強くなり、つやつやした見た目になります。
$ \alpha $
毛の表面の小さなオフセット角度です。以下の図のようにキューティクル層(Cuticle)層の起き上がりを表現します。通常は2度を使うそうです。
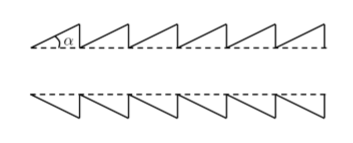
Matt Pharr, "01 THE IMPLEMENTATION OF A HAIR SCATTERING MODEL"より
[1] LING-QI YAN, HENRIK WANN JENSEN, RAVI RAMAMOORTHI, "An Efficient and Practical Near and Far Field Fur Reflectance Model"より、コサックギツネの毛の顕微鏡写真
基本はこれで質感を指定しますが、この他に必要な変数についても確認します。
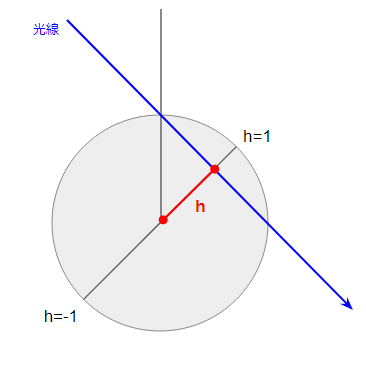
$ h $
こちらは直接的に質感を決めるためではなく、光線と円筒の幾何学な交差位置を表すパラメータで、毛の太さがどんなものでも-1~1 に正規化した値を使います。これは事前に決めておくことはせず、実際の光線と毛の衝突判定のフェーズで算出しておく必要があります。このパラメータを活用して、毛の内部でおこる屈折現象や吸収がどの程度起こるかなどの計算を行います。
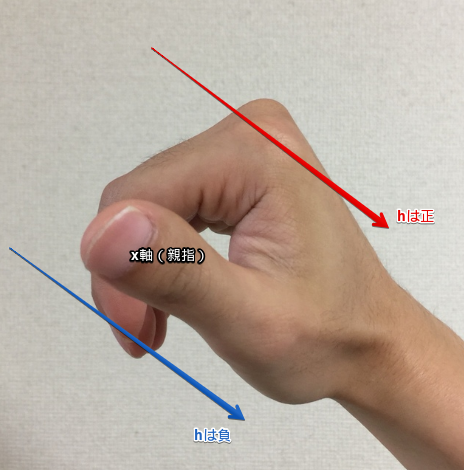
注意点として、hはきちんと正負を正しく与える必要があるという点があります。今回の座標系では、右手の親指をx軸と見た場合、指の回転方向に自然に差し込む場合に負になります。これも衝突判定のフェーズで行っておく必要があります。
$ \omega_i, \omega_o $
それぞれ、光源側のベクトル, カメラ側のベクトルです。
以上がBSDFの評価に必要なパラメータになります。これらが揃えば、BSDFを評価して毛や髪をレンダリングすることが可能になります。入力と出力がはっきりしただけでもプログラマ的には安心して進められるのではないでしょうか。
経度(longitudinal)拡散関数
さてそろそろ中身について詳しく迫っていきます。まずは経度(longitudinal)拡散関数 $ M_p $ からです。これは以下のような関数で表現します。
M_{ p }\left( \theta _{ i },\theta _{ o } \right) =\frac { 1 }{ 2v\sinh { \frac { 1 }{ v } } } { e }^{ -\frac { \sin { \theta _{ i } } \sin { \theta _{ o } } }{ v } }I_{ 0 }\left( \frac { \cos { \theta _{ o } } \cos { \theta _{ i } } }{ v } \right)
まず $ v $ ですが、これは先のパラメータには存在していなかったパラメータです。ですが、これは$ \beta_m $ からの算出を後述しますので、パラメータが増えるわけではありません。
次に $ I_0 $ 関数ですが、これは第一種変形ベッセル関数という関数です。調べてみると、ベッセルの微分方程式の特殊解?の一つのようですが、あまり良くわからないのですが、以下のように無限級数で定義されるそうです。
I_{ \alpha }\left( x \right) =\sum _{ m=0 }^{ \infty } \frac { 1 }{ m!\Gamma \left( m+\alpha +1 \right) } \left( \frac { x }{ 2 } \right) ^{ 2m+\alpha }
今回 $ \alpha = 0 $ のため、
I_{ 0 }\left( x \right) =\sum _{ m=0 }^{ \infty } \frac { 1 }{ m!\Gamma \left( m+1 \right) } \left( \frac { x }{ 2 } \right) ^{ 2m }
でありまた、
\Gamma \left( n+1 \right) =n!
であるため、
I_0\left(x\right)=\sum _{m=0}^n\frac{1}{\left(m!\right)^2}\left(\frac{x}{2}\right)^{2m}
を使うことができます。例えばPBRTの実装では、$ m=10 $でハードコードされていました。
愚直にコードにするのも一つですが、
\sum _{ m=0 }^{ n } \frac { 1 }{ \left( m! \right) ^{ 2 } } \left( \frac { x }{ 2 } \right) ^{ 2m }=\sum _{ m=0 }^{ n } X_{ m }
とおくと、
X_{ m }=\frac { 1 }{ \left( m! \right) ^{ 2 } } \left( \frac { x }{ 2 } \right) ^{ 2m }\\ X_{ m+1 }=\frac { 1 }{ \left( m\cdot m! \right) ^{ 2 } } { \left( \frac { x }{ 2 } \right) }^{ 2 }{ \left( \frac { x }{ 2 } \right) }^{ 2m }
と一つ前の項が再利用できる数字があるため、そこを利用して効率的良く計算することが可能です。
$ 0!=1 $ だけ気をつけてコードにすると、以下のようになります。
inline double I0(double x, int n = 10) {
double sum = 0.0;
double fact_m = 1.0;
double x_over_2_pow_2m = 1.0;
const double x_over_2 = x * 0.5;
for (int m = 0; m < n; ++m) {
if (m != 0) {
fact_m *= m;
}
sum += 1.0 / (fact_m * fact_m) * x_over_2_pow_2m;
x_over_2_pow_2m *= x_over_2 * x_over_2;
}
return sum;
}
この方法を一般に、ホーナー法と言うのでした。
しかしまだ問題があります。経度(longitudinal)拡散関数において、
M_{ p }\left( \theta _{ i },\theta _{ o } \right) =\frac { 1 }{ 2v\sinh { \frac { 1 }{ v } } } { e }^{ \frac { \sin { \theta _{ i } } \sin { \theta _{ o } } }{ v } }I_{ 0 }\left( \frac { \cos { \theta _{ o } } \cos { \theta _{ i } } }{ v } \right)
$ v $ が小さな場合、特に $ v < 0.1 $ のケースで、項の数カ所で数値がとても大きな数字をとり、関数の値が不安定になるという問題があります。そこで、
M_{ p }\left( \theta _{ i },\theta _{ o } \right) \simeq exp\left( \log { \left( I_{ 0 }\left( \frac { \cos { \theta _{ o } } \cos { \theta _{ i } } }{ v } \right) \right) } +\frac { \sin { \theta _{ i } } \sin { \theta _{ o } } }{ v } -\frac { 1 }{ v } +0.6931+\log { \frac { 1 }{ 2v } } \right)
を使うことでこの問題を回避することが、Eugene d'Eon氏により提案されています。
さらにもう一つ問題があり、後者の関数近似の場合、$ I_{ 0 } $ に結構大きな数字が入る可能性があり、これは級数展開を限られた回数でしか評価できない場合に不利になります。
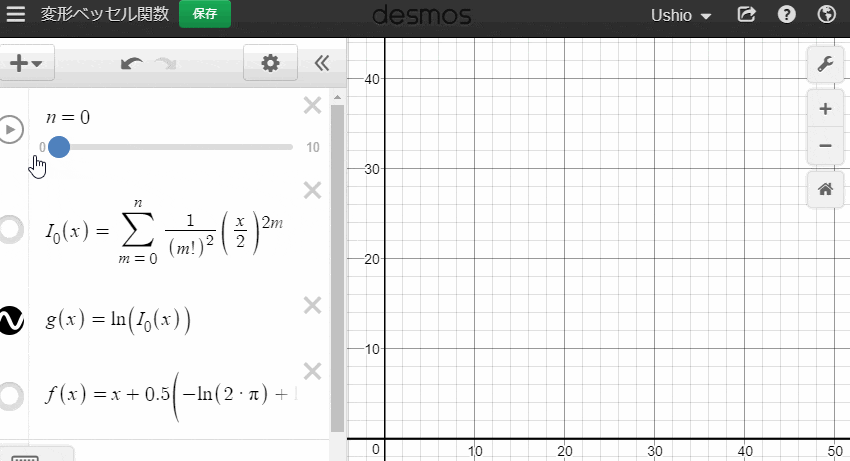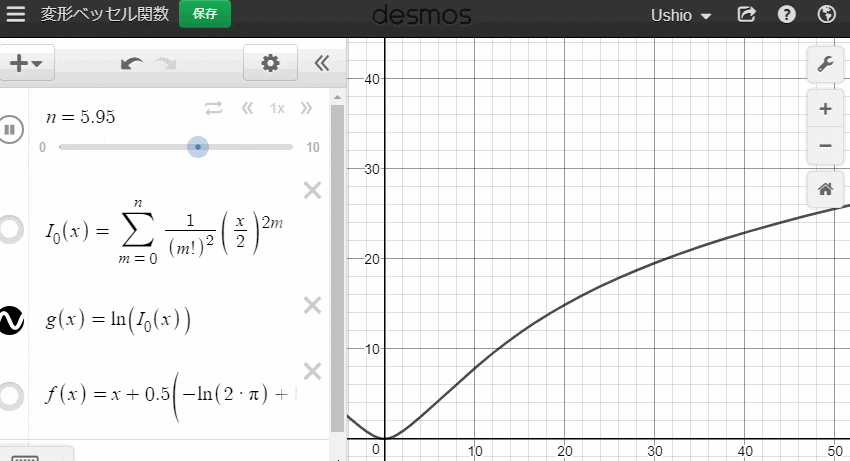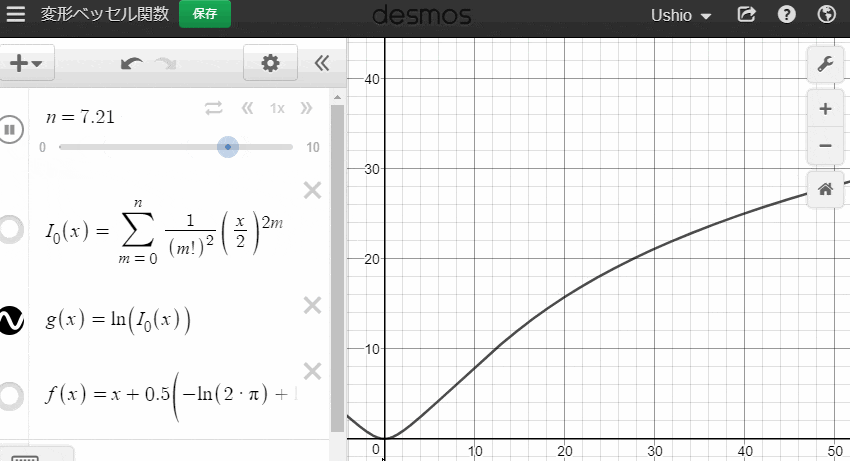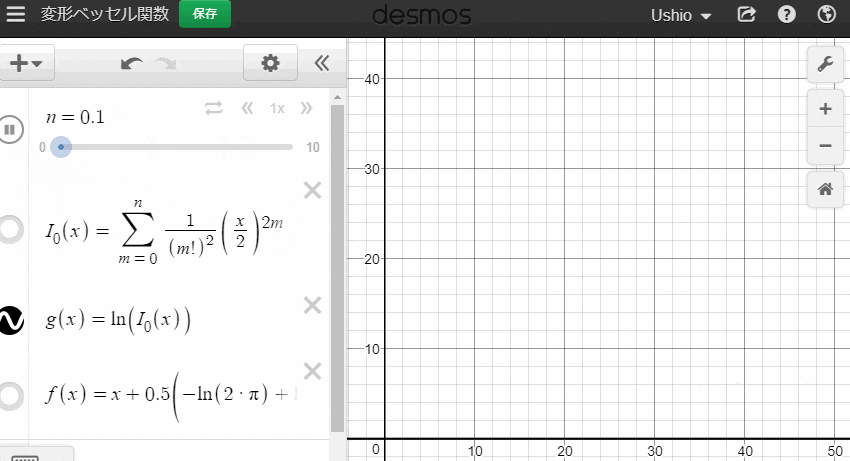
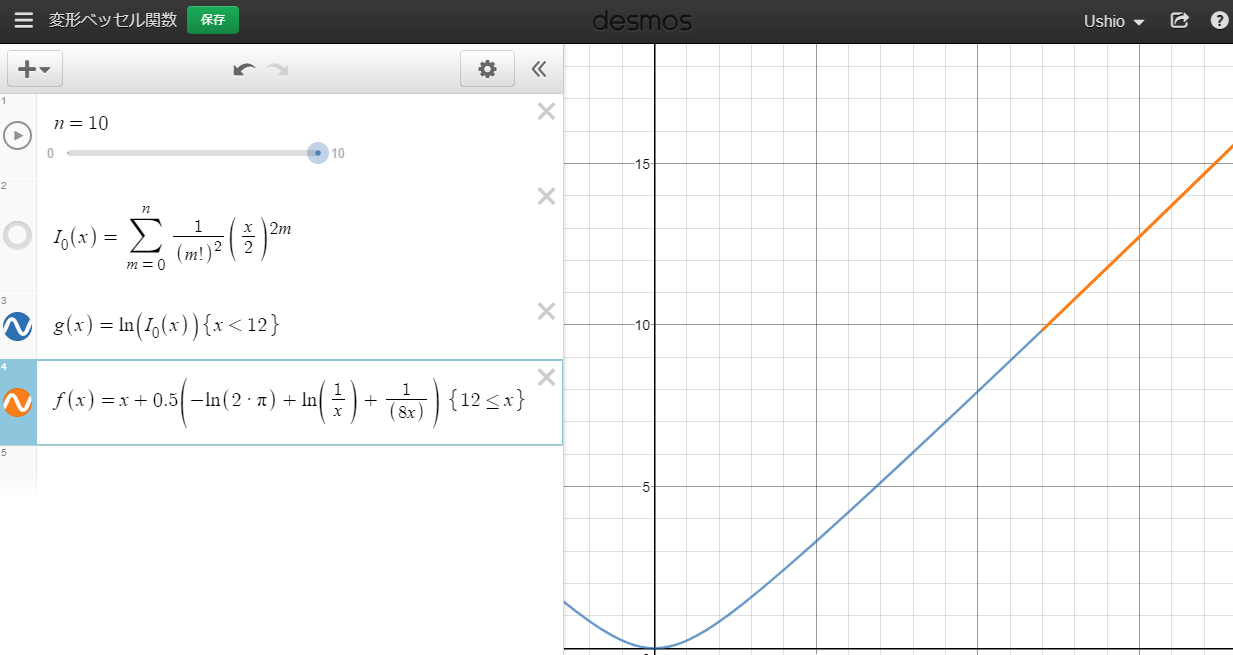
$ \ln \left(I_0\left(x\right)\right) $ をdesmosで観察してみましょう。
xが0に十分に近ければ、nが小さくても数値がすぐ安定するように見えますが、xが0から離れた箇所についてはなかなかつらそうです。
そこで、$ 12 < x $ の場合、
\log \left( I_{ 0 }\left( x \right) \right) \simeq x+0.5\left( -\log { \left( 2\cdot \pi \right) } +\log { \left( \frac { 1 }{ x } \right) } +\frac { 1 }{ \left( 8x \right) } \right)
を使うと良いそうです。こちらもEugene d'Eon氏により提案されています。
こちらもグラフで確認しておきましょう。
以上を踏まえると、実装は以下のようになります。
inline double LogI0(double x) {
if (x > 12.0) {
return x + 0.5 * (-std::log(2.0 * glm::pi<double>()) + std::log(1.0 / x) + 1.0 / (8.0 * x));
}
return std::log(I0(x));
}
inline double Mp(double sinThetaI, double cosThetaI, double sinThetaO, double cosThetaO, double v) {
double a = cosThetaI * cosThetaO / v;
double b = sinThetaI * sinThetaO / v;
double mp = (v <= 0.1) ?
(glm::exp(LogI0(a) - b - 1.0 / v + 0.6931 + glm::log(1.0 / (2.0 * v)))) :
(glm::exp(-b) * I0(a)) / (glm::sinh(1.0 / v) * 2.0 * v);
return mp;
}
ここで、sinThetaI, cosThetaI, sinThetaO, cosThetaOについては、
double sinThetaO = wo.x;
double cosThetaO = SafeSqrt(1.0 - Sqr(sinThetaO));
double sinThetaI = wi.x;
double cosThetaI = SafeSqrt(1.0 - Sqr(sinThetaI));
というように求めることができます。
これは、
であり、
\sin ^{ 2 }{ \theta } +\cos ^{ 2 }{ \theta } =1\\ \sin ^{ 2 }{ \theta } =1-\cos ^{ 2 }{ \theta } \\ \sin { \theta } =\sqrt { 1-\cos ^{ 2 }{ \theta } }
であるためです。
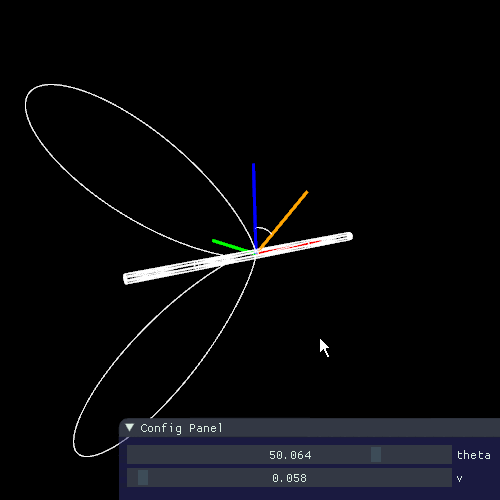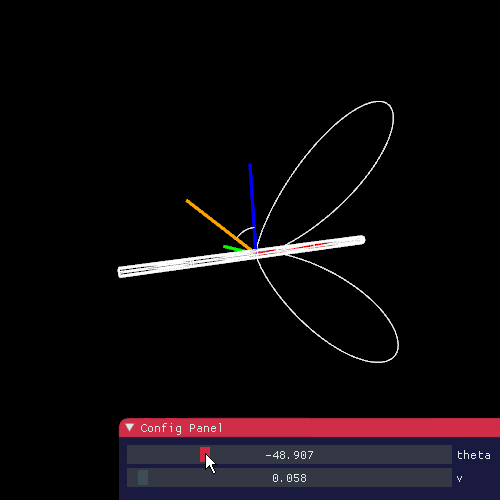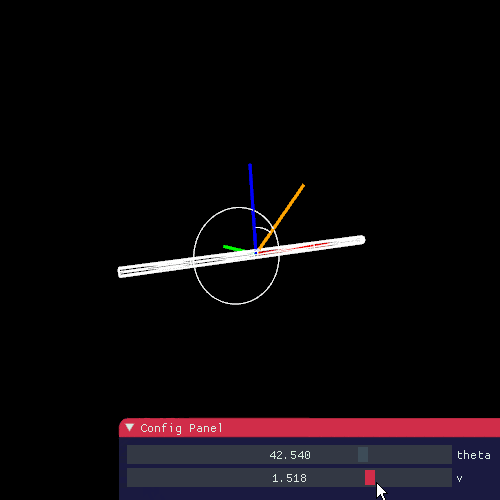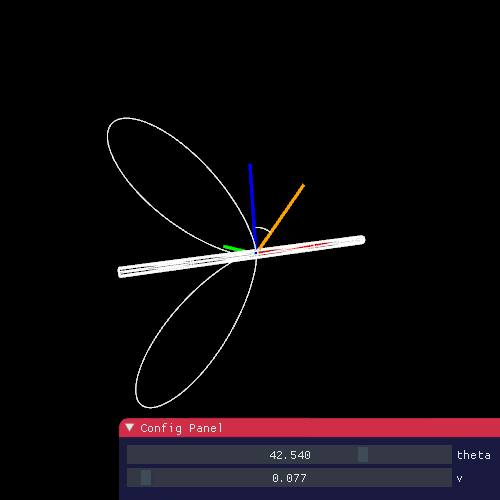
これで実際にどんな形の関数になるかを確認しますと、
vが小さければ、ハイライトを発生しそうです。実際、レンダリングの例としては、

[6] Matt Pharr, "01 THE IMPLEMENTATION OF A HAIR SCATTERING MODEL" より
と、イメージが合うのではないでしょうか。
ところでまだ $ v $ と $ \beta_m $ の関係性を紹介していませんでした。
$ v $ と $ \beta_m $ の関係性については、pの各段階によって少し違うようです。こちらはいきなりコードで紹介しますと、
inline std::array<double, pMax + 1> betam_to_v(double bm) {
std::array<double, pMax + 1> vs;
vs[0] = Sqr(0.726 * bm + 0.812 * Sqr(bm) + 3.7 * Pow<20>(bm));
vs[1] = 0.25 * vs[0];
vs[2] = 4.0 * vs[0];
for (int p = 3; p <= pMax; ++p)
vs[p] = vs[2];
return vs;
}
ただし、
template <int n>
static double Pow(double v) {
static_assert(n > 0, "Power can’t be negative");
double n2 = Pow<n / 2>(v);
return n2 * n2 * Pow<n & 1>(v);
}
template <> double Pow<1>(double v) { return v; }
template <> double Pow<0>(double v) { return 1.0; }
inline double Sqr(double x) {
return x * x;
}
を使うようです。ちょっとしたテンプレート特殊化のテクニックが用いられていますが、整数のべき乗を求めているだけになります。このように繰り返し自分を2乗していく手法を、繰り返し自乗法と呼び、効率的に計算できるように工夫がなされていることがわかります。
この変換により、$ \beta_m $ で見た目に直観的な表面の粗さの制御が可能になるとのことです。
吸収関数
吸収関数 $ A_p $ は、まずランベルト・ベールの法則を考慮します。といいつつも、同時にフレネルによる分断も同時に考慮します。
xを、コルテックス層(Cortex)およびメデュラ層(Medulla)を通過するときの長さとすると、吸収係数Tは、
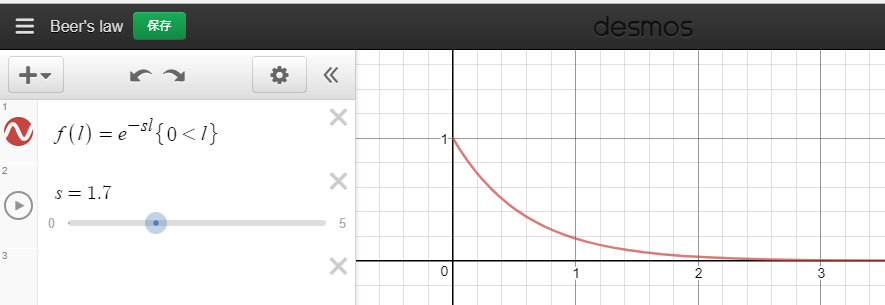
T\left( x \right) =e^{ -\sigma _{ a }x }
となります。これは例えば、以下のような関数になります。
$ \sigma _{ a } = 0 $ の場合、Tは常に1になるため、まったく吸収されないことを意味し、$ \sigma _{ a } $ が大きくなるにつれ、距離に対しての減衰がより大きくなります。
では通過するときの距離の計算ですが、ちょっとうまく理解できなかったので、コードを紹介するだけにとどめます・・・すみません。hや $cos{\theta}, \sin{\theta}$ から求めることができるようです。[4] [MARSCHNER S. R., JENSEN H. W., CAMMARANO M., WORLEY S., HANRAHAN P., "Light Scattering from Human Hair Fibers"] (http://www.graphics.stanford.edu/papers/hair/hair-sg03final.pdf) の"B The Bravais index"に導出が載っています。
double etap = glm::sqrt(eta * eta - Sqr(sinThetaO)) / cosThetaO;
double sinGammaT = h / etap;
double cosGammaT = SafeSqrt(1 - Sqr(sinGammaT));
// 通過する距離
double l = 2.0 * cosGammaT / cosThetaT;
// 通過するときの吸収係数
Vec3 T = glm::exp(-sigma_a * l);
また、Tは、以下のように何回内部で屈折しようが、通過する距離は一定であるため、一度Tを算出すればそれを使いまわすことができます。後に説明するフレネル成分も同様のことが言えるため、一度係数を算出したらそれを使いまわすことにします。
[6] Matt Pharr, "01 THE IMPLEMENTATION OF A HAIR SCATTERING MODEL" より
次にキューティクル層(Cuticle)に光がぶつかった時にはフレネル項を考慮する必要があります。
これには絶縁体のフレネル反射を使います。PBRTの実装では毛/髪 専用ではありませんが、以下のような実装されており、
inline double FrDielectric(double cosThetaI, double etaI, double etaT) {
cosThetaI = glm::clamp(cosThetaI, -1.0, 1.0);
bool entering = cosThetaI > 0.f;
if (!entering) {
std::swap(etaI, etaT);
cosThetaI = std::abs(cosThetaI);
}
// Compute _cosThetaT_ using Snell's law
double sinThetaI = std::sqrt(std::max(0.0, 1.0 - cosThetaI * cosThetaI));
double sinThetaT = etaI / etaT * sinThetaI;
// Handle total internal reflection
if (sinThetaT >= 1.0) return 1;
double cosThetaT = std::sqrt(std::max(0.0, 1.0 - sinThetaT * sinThetaT));
double Rparl = ((etaT * cosThetaI) - (etaI * cosThetaT)) / ((etaT * cosThetaI) + (etaI * cosThetaT));
double Rperp = ((etaI * cosThetaI) - (etaT * cosThetaT)) / ((etaI * cosThetaI) + (etaT * cosThetaT));
return (Rparl * Rparl + Rperp * Rperp) * 0.5;
}
etaI=1.0, etaT=1.55とし、$ \cos { \theta } $ をxにプロットしてみますと、
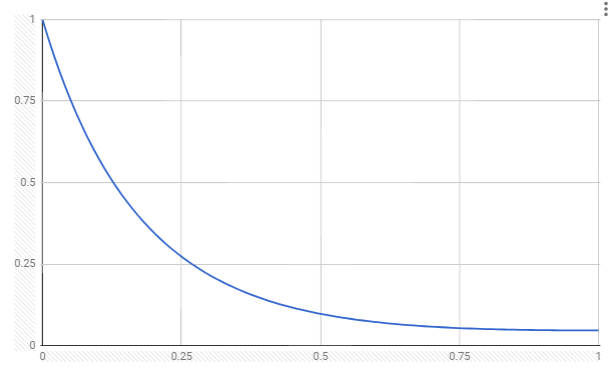
という形になり、これをキューティクル層(Cuticle)を反射・通過するときにこの値を利用します。角度が水平に近い( $ \cos { \theta } $ が0に近い)ほど反射量が多く、角度が垂直に近い( $ \cos { \theta } $ が1に近い)ほど反射は少なく、透過していることがわかります。
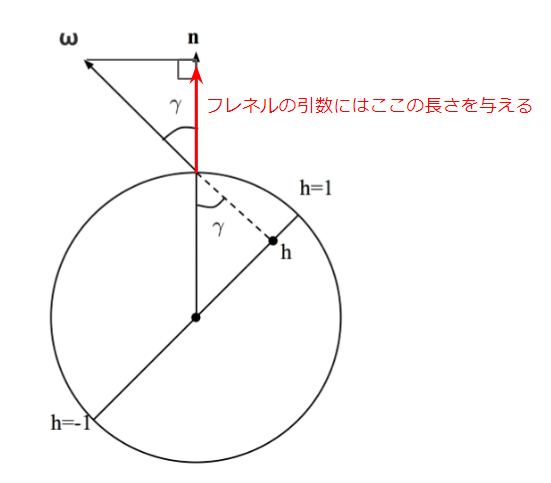
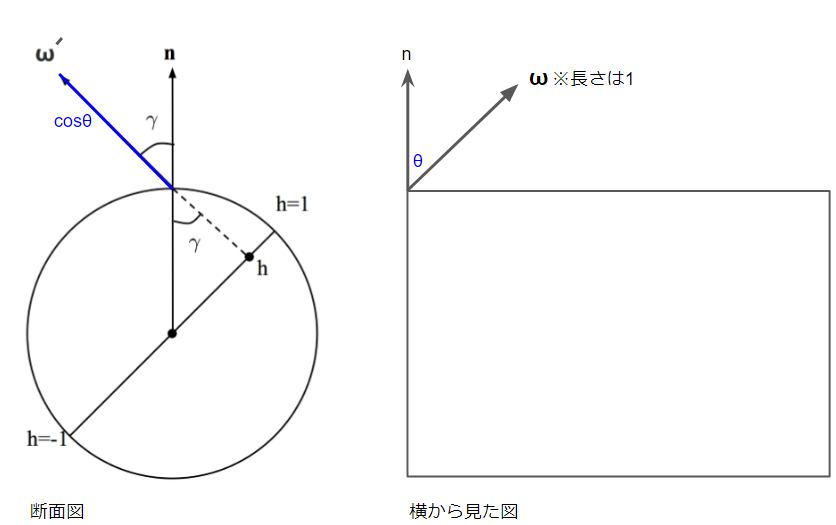
というわけで、この関数を評価する時には入射ベクトルの $ \cos { \theta_{fesnel} } $ が必要です。これは結局入射ベクトルを法線に投射したときの長さであると言えます。
これを計算するためには、まずωを平面に投射したω’を考えます。こちらも投射の考え方により、長さが $ \cos { \theta_{fesnel} } $ になります。
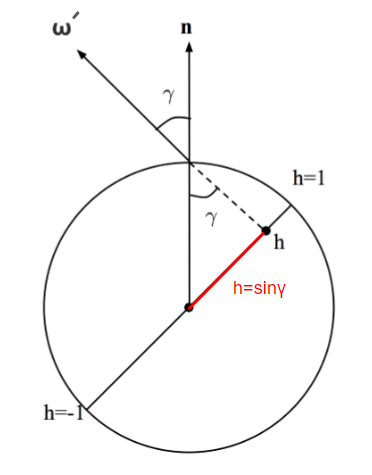
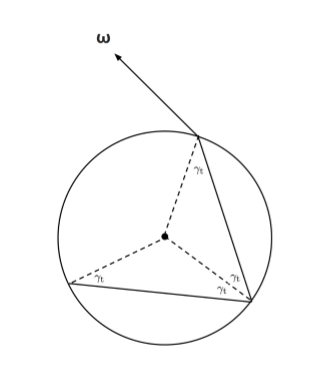
一方、$ h $ により $ \cos { \gamma } $ を求めることができます。なぜかというと図のように、
$ h=\sin { \gamma } $ であり、
\sin ^{ 2 }{ \gamma } +\cos ^{ 2 }{ \gamma } =1\\ \cos ^{ 2 }{ \gamma } =1-\sin ^{ 2 }{ \gamma } \\ \cos { \gamma } =\sqrt { 1-\sin ^{ 2 }{ \gamma } } \\ \cos { \gamma } =\sqrt { 1-{ h }^{ 2 } }
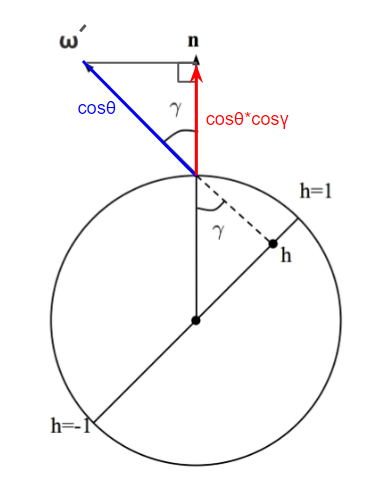
であるためです。これを使うと、結局フレネルを評価するためのコサインは、
と $ \cos { \theta } \sqrt { 1-{ h }^{ 2 } } $ となります。
結果的にフレネル項を求めるコードは、
double cosGammaO = SafeSqrt(1.0 - h * h);
double cosTheta = cosThetaO * cosGammaO;
double f = FrDielectric(cosTheta, 1.0, eta);
のようになりました。
さて、そろそろpの各段階を思い出しつつ、Apの各段階における係数を算出する関数を考えていきます。
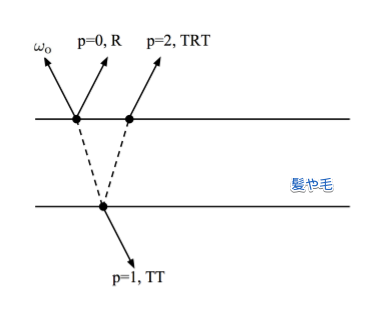
[6] Matt Pharr, "01 THE IMPLEMENTATION OF A HAIR SCATTERING MODEL" より
inline std::array<Vec3, pMax + 1> Ap(double cosThetaO, double eta, double h, const Vec3 &T);
まずp=0においては、反射であり、まだ吸収は考慮しなくていいので、
ap[0] = Vec3(f);
となります。次にp=1ですが、フレネルの分(出入りで2回分)と、コルテックス層(Cortex),メデュラ層(Medulla)を1度通過しますのでTを1回合わせまして、
ap[1] = Sqr(1 - f) * T;
となります。さらにp=2ですが、今までの分に加えて、フレネルがもう一回増えているのと、さらにコルテックス層(Cortex),メデュラ層(Medulla)をもう1度通過しますので、
ap[2] = ap[1] * T * f;
というかんじです。これはp=2以降は一般化して、
A_{ p }={ \left( 1−f \right) }^{ 2 }T^{ p }f^{ p−1 }
と書くことができます。
必ず入って出るため、フレネル成分が2乗になっている点、pが1増えると、フレネルの分と吸収係数が1回ずつ増える点が理解できます。
ただ、p=3以降はすべてp=3にまとめ上げると先に述べていました。なので、残りの吸収係数を全部足してまとめてしまいます。
\sum _{ p=3 }^{ n }{ { \left( 1−f \right) }^{ 2 }T^{ p }f^{ p−1 } }
幸いにしてこれは解くことができます。
\sum _{ p=3 }^{ n }{ { \left( 1−f \right) }^{ 2 }T^{ p }f^{ p−1 } } =\sum _{ p=0 }^{ n }{ { \left( 1−f \right) }^{ 2 }\frac { 1 }{ f } T^{ p }f^{ p } } -\sum _{ p=0 }^{ 2 }{ { \left( 1−f \right) }^{ 2 }\frac { 1 }{ f } T^{ p }f^{ p } } \\ \sum _{ p=0 }^{ n }{ { \left( 1−f \right) }^{ 2 }\frac { 1 }{ f } T^{ p }f^{ p } }
これは初項 $ a $, 公比 $ r $ の 等比級数和として考えることができ、
r=Tf\\ a={ \left( 1−f \right) }^{ 2 }\frac { 1 }{ f } \\ S_{ n }=\frac { a\left( 1-{ r }^{ n } \right) }{ 1-r } \\ S_{ n }=\frac { { \left( 1−f \right) }^{ 2 }\frac { 1 }{ f } \left( 1-{ \left( Tf \right) }^{ n } \right) }{ 1-Tf }
よって、
\sum _{ p=3 }^{ n }{ { \left( 1−f \right) }^{ 2 }T^{ p }f^{ p−1 } } =S_{ \infty }-S_{ 2 }\\ =\lim _{ n\rightarrow \infty }{ \frac { { \left( 1−f \right) }^{ 2 }\frac { 1 }{ f } \left( 1-{ \left( Tf \right) }^{ n } \right) }{ 1-Tf } } -\frac { { \left( 1−f \right) }^{ 2 }\frac { 1 }{ f } \left( 1-{ T }^{ 3 }{ f }^{ 3 } \right) }{ 1-Tf } \\ =\frac { { \left( 1−f \right) }^{ 2 }\frac { 1 }{ f } }{ 1-Tf } -\frac { { \left( 1−f \right) }^{ 2 }\frac { 1 }{ f } \left( 1-{ T }^{ 3 }{ f }^{ 3 } \right) }{ 1-Tf } \\ =\frac { { \left( 1−f \right) }^{ 2 }\frac { 1 }{ f } }{ 1-Tf } \left( 1-1+{ T }^{ 3 }{ f }^{ 3 } \right) \\ =\frac { { \left( 1−f \right) }^{ 2 }\frac { 1 }{ f } }{ 1-Tf } \left( { T }^{ 3 }{ f }^{ 3 } \right) \\ =\frac { { \left( 1−f \right) }^{ 2 }\left( { T }^{ 3 }{ f }^{ 2 } \right) }{ 1-Tf }
となります。ただし、$ |Tf| < 1 $ であるとして計算します。フレネル項が1を超えませんし、Tも1を超えることはありません。$ |Tf| = 1 $ のケースは無くはない気もしますが、結構なレアケースであり実用上は考える必要が無いようです。
さらに、
{ \left( 1−f \right) }^{ 2 }{ T }^{ 2 }f
の部分については、ap[2]ですでに計算されていますので、
\frac { { T }{ f } }{ 1-Tf }
だけ評価すればよく、最後の項は、
ap[pMax] = ap[pMax - 1] * f * T / (Vec3(1.0) - T * f);
となります。これで吸収関数の準備は整いました。
※Apについては、一般的には次に解説するNpに含むらしいです。別な文献を当たる時は注意が必要かもしれません。
もふもふレンダリング入門(2)に続きます。
[1] LING-QI YAN, HENRIK WANN JENSEN, RAVI RAMAMOORTHI, "An Efficient and Practical Near and Far Field Fur Reflectance Model"
[2] Kajiya, Key, "RENDERING FUR WITH THREE DEMENSIIONAL TEXTURES"
[3] Thorsten Scheuermann, ATI Research, "Hair Rendering and Shading"
[4] [MARSCHNER S. R., JENSEN H. W., CAMMARANO M., WORLEY S., HANRAHAN P., "Light Scattering from Human Hair Fibers"] (http://www.graphics.stanford.edu/papers/hair/hair-sg03final.pdf)
[5] Shinji Ogaki, Yusuke Tokuyoshi, Sebastian Schoellhammer, Square Enix Co., Ltd. "An Empirical Fur Shader"
[6] Matt Pharr, "01 THE IMPLEMENTATION OF A HAIR SCATTERING MODEL"