はじめに
こちらの記事は以前投稿した「【機械学習】初心者が競艇予想ツール作成して金儲け大作戦」
のディープラーニング編となります。
ディープラーニングは今や書店のIT関連のコーナーに行けば、
必ず本が置いてあるくらいメジャーなものになりつつあります。
(どなたでも一度は「表紙に魚が書かれている本」を見たことはあると思います。)
今回はディープラーニングについての簡単な説明と代表的なフレームワークの1つである
**Keras**の使い方をご紹介します。
実際に手を動かしてみると、意外と簡単にディープラーニングの構築ができますので、この記事が
「これからディープラーニングを学びたい!」と考えている方の助けになれば幸いです!
(ちなみに、実際にディープラーニングを使用して競艇予想してみました!
そちらについては別記事を投稿する予定ですので、お楽しみに!)
--2019/9/9追記--
実装編の記事も投稿いたしました!
・【ディープラーニング】初心者が競艇予想ツールを作成するために学んだディープラーニングについて_実装編①
・【ディープラーニング】初心者が競艇予想ツールを作成するために学んだディープラーニングについて_実装編②
注意
この記事は「ディープラーニングって何かよくわからないけど、とりあえず競艇予想してお金儲けしたい!」と考えたド素人が学んだ知識をアウトプットするための記事でございます。
詳しいディープラーニングの理論につきましてはこの記事の最後に参考文献をご紹介いたしますので、
そちらをご参照いただきたいです。
環境
開発環境は「【機械学習】初心者が競艇予想ツール作成して金儲け大作戦」と同様に
Google Colaboratoryを使用しています。
言語は**Python3**
フレームワークは**Keras**です。
アジェンダ
・ディープラーニングってそもそも何?
・**Keras**ってそもそも何?
・**Keras**の使い方
・まとめ
・参考文献
ディープラーニングってそもそも何?
ディープラーニング(深層学習)とは、人間が自然に行うタスクをコンピュータに学習させる機械学習の手法のひとつです。人工知能(AI)の急速な発展を支える技術であり、その進歩により様々な分野への実用化が進んでいます。
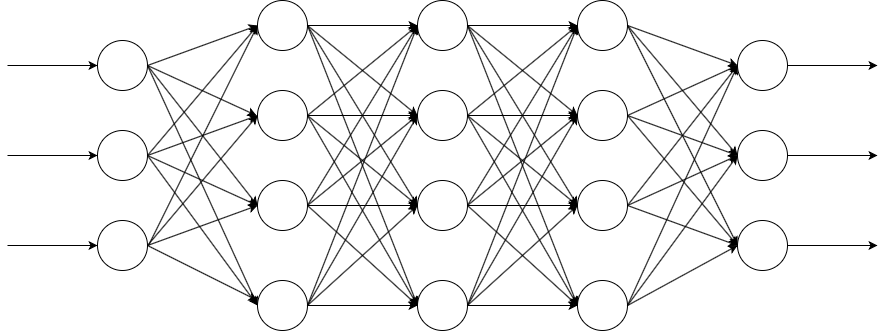
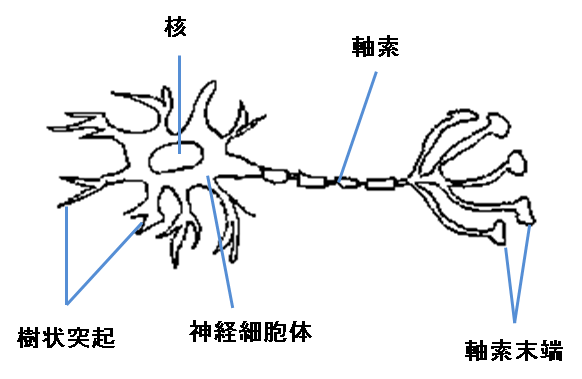
ディープラーニングの技術は、人間の神経細胞(ニューロン)の仕組みを模したシステムであるニューラルネットワークがベースになっています。ニューラルネットワークを多層にして用いることで、データに含まれる特徴を段階的により深く学習することが可能になります。
上記のサイトにて簡潔かつ端的に説明いただいておりますが、特徴としては以下の通りです。
・ニューラルネットワークをベースとしている。
・ニューラルネットワークを多層化し、データに含まれる特徴をより深く学習する。
この説明の中で出てきたニューラルネットワークがディープラーニングを学ぶ上での基礎となります。
ニューラルネットワークについて
ニューラルネットワークとは生物の神経細胞(ニューロン)が構成するネットワーク(人間の脳内ネットワーク)を元に作成したコンピュータネットワークです。
ニューラルネットワークの構成として、ユニットと**層(レイヤー)**があります。
・ユニット
ユニットはニューロンを元に定義されたものです。
各ユニットは入力を受け取り、計算した結果を出力する仕組みとなっています。
ちなみにこれらの画像は以下のサイトから拝借いたしました。
・人工知能であそぶ
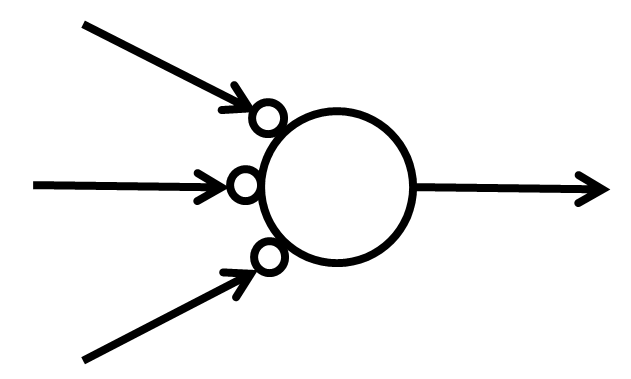
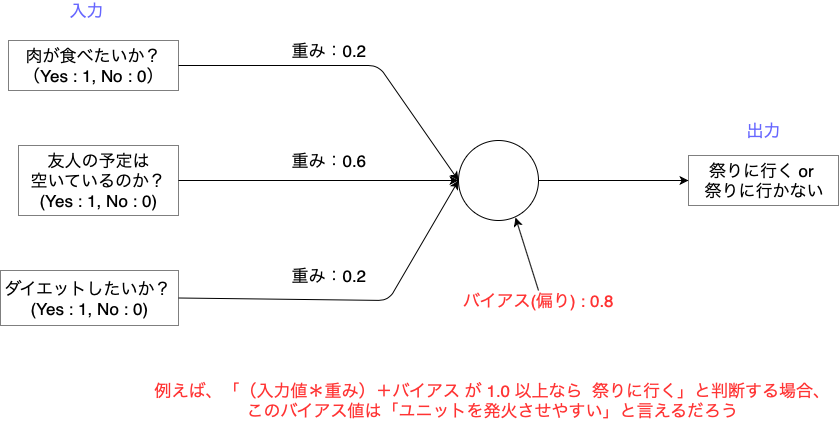
上の画像ですと、ユニットに向かって矢印が3本伸びています。
このユニットは3要素の入力を受け取り、計算した結果を次のユニットに出力します。
続いて各ユニットでの計算について説明いたします。
ユニットでの計算では入力値・重み・バイアス・活性化関数を使用します。
重み
重み とは入力された値をどれくらい重要視するのかを定義する値です。
そして、ニューラルネットワークのユニットは学習を進めることで、
この重みの値を自動で調整します。
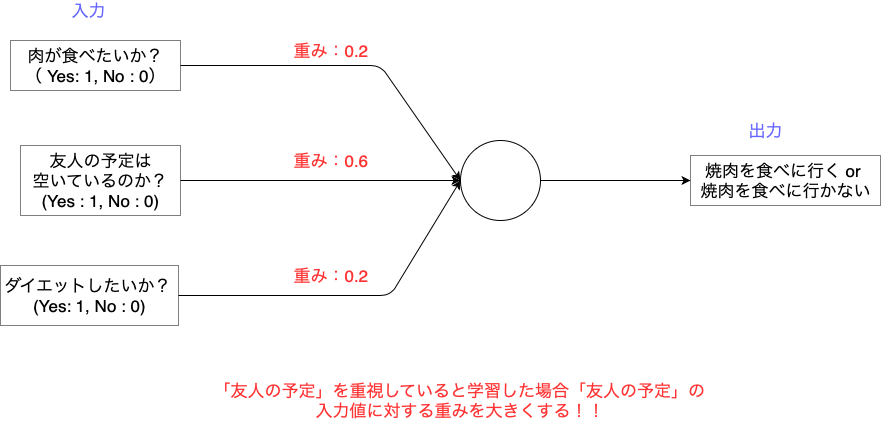
例えば、「焼肉を食べに行くべきか」を判定するときに
「肉が食べたいか?」・「友人の予定」・「ダイエットしたいか?」を入力値とします。
このとき、「友達と一緒なら焼肉食べようかな...」
と考える人が多かった場合、ユニットは「友人の予定」という入力を重要視します。
この結果、ユニットは「友人の予定」の重みをより大きくするように学習します。
バイアス
バイアス とはユニットの意思決定の偏りです。
また、ニューラルネットワークのユニットは学習を進めることで、
バイアスの値も自動で調整します。
ユニットの出力値yは、活性化関数をf(u)とすると以下の式で求めます。
y = f(u)
u =(入力値(x_1,x_2,...x_n)*重さ(w_1,w_2,...w_n))+バイアス(b)
ですので、バイアスの値はユニットの発火のしやすさに影響すると言われています。
重みやバイアスの考え方についてはこちらのサイトを参考とさせていただきました!
とてもわかりやすく説明されているため、ぜひご参照ください。
活性化関数
活性化関数 は入力情報の総和を出力信号に変換する関数です。
上記のバイアスの説明でも記載いたしましたが、
ユニットでは以下の値を活性化関数を用いて変換します。
((入力値(x_1,x_2,...x_n)*重さ(w_1,w_2,...w_n))+バイアス(b)
活性化関数を入力情報の総和に対して使用し、出力信号に変換することで
ニューラルネットワークは複雑な表現を行えるようになります。
活性化関数にはいくつか種類があります。
ここではよく聞く3種類の活性化関数をご紹介します。
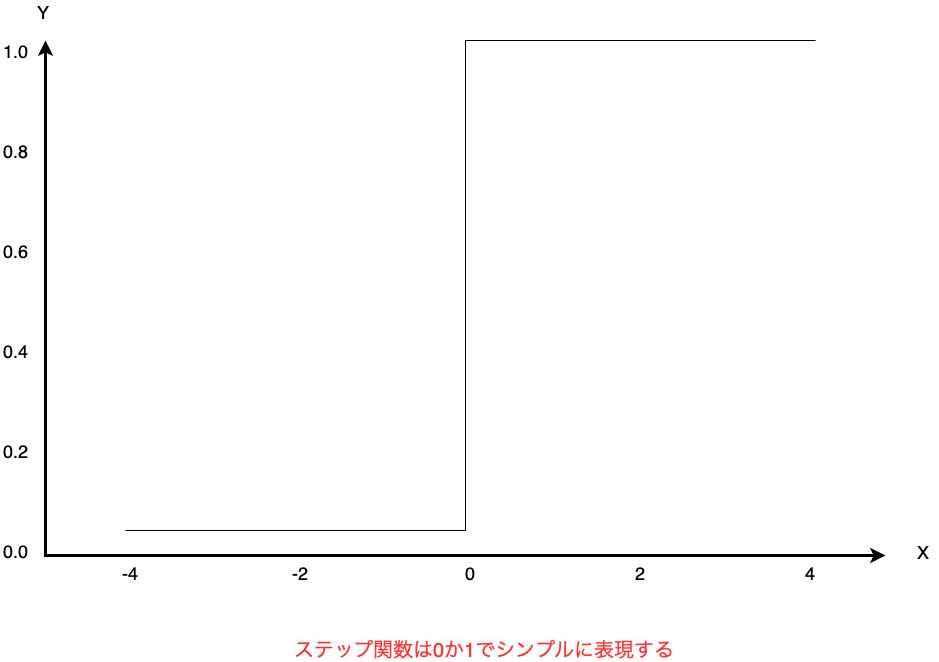
・ステップ関数
ステップ関数は入力値をX、出力値をYとすると、
以下のグラフで表現される関数です。
グラフどおり、出力値を0か1で表現する非常にシンプルな関数です。
数式で表現すると以下の式になります。
y=\begin{cases}0 & (x \leq 0)\\1 & (x > 0)\end{cases}
シンプルな点がメリットではありますが、
反面0と1の間の状態を表現できないというデメリットもあります。
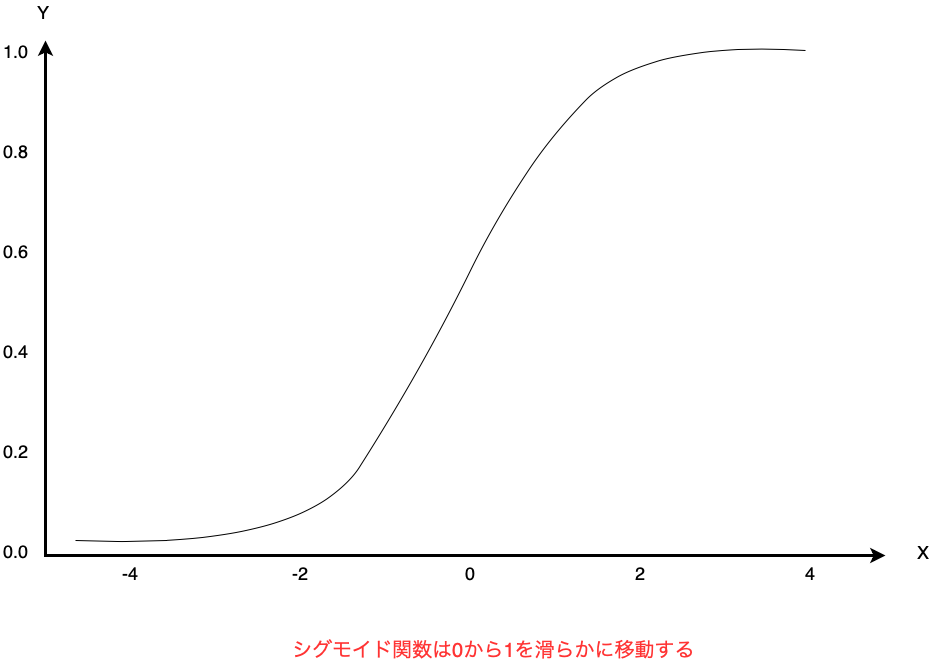
・シグモイド関数
シグモイド関数は入力値をX、出力値をYとすると、
以下のグラフで表現される関数です。
シグモイド関数は、出力値が0と1の間で滑らかに変化する関数です。
数式で表現すると以下の式になります。
y=\frac{1}{1+exp(-x)}
Xが小さくなるとYは0に近づき、
Xが大きくなるとYは1に近づきます。
シグモイド関数は微分が扱いやすいという特性があるため、
古くからニューラルネットワークで使用されていました。
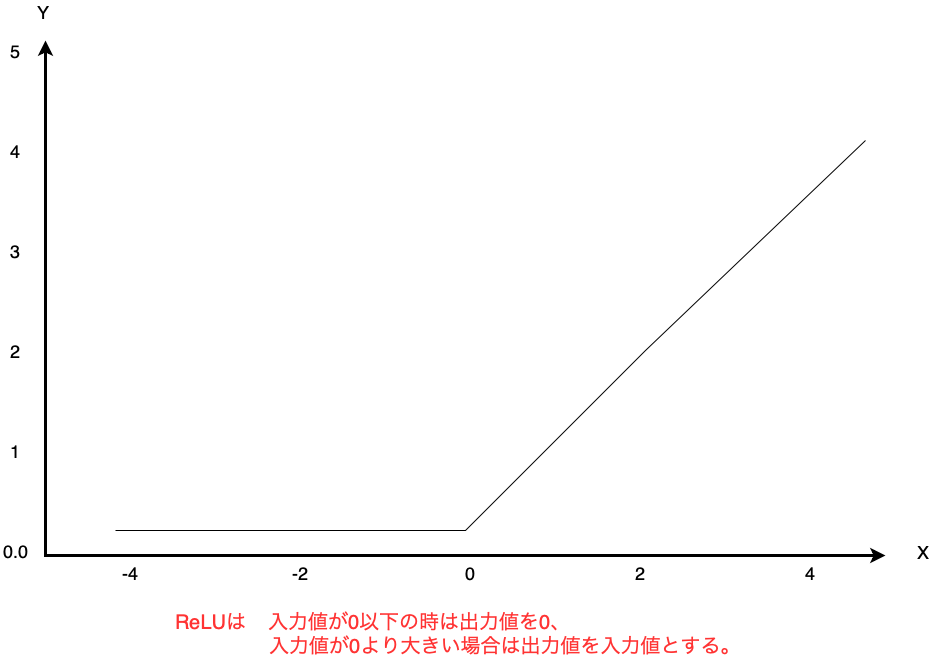
・ReLU
ReLUは入力値をX、出力値をYとすると、
以下のグラフで表現される関数です。
ReLUは、入力値 > 0の範囲でのみ立ち上がるのが特徴的な関数です。
数式で表現すると以下の式になります。
y=\begin{cases}0 & (x \leq 0)\\ x & (x > 0)\end{cases}
Xが0以下の時はYは0、
Xが0より大きい時はY=Xとなります。
ReLUはシンプルかつ層(レイヤー)の数が多くなっても安定した学習が
可能であるため、最近のディープラーニングではよく使用されています。
以上がユニットの説明です。
続いて層(レイヤー)の説明です。
・層(レイヤー)
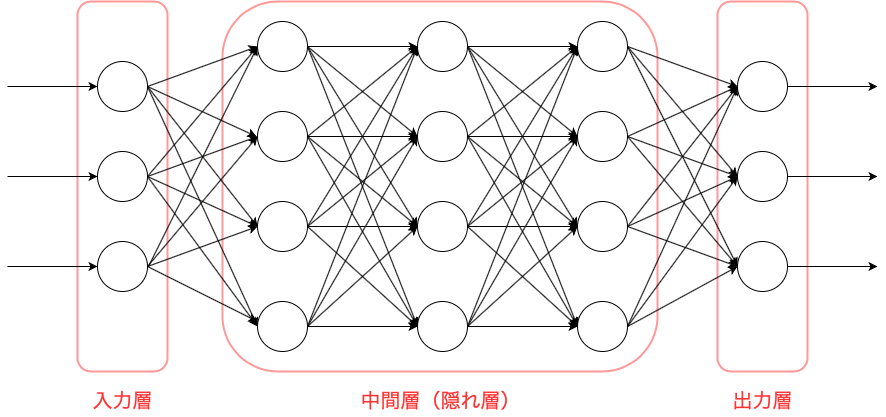
**ニューラルネットワークの層(レイヤー)**はユニットをまとめたものです。
層の種類としては大きく3つに分かれます。
・入力層・・・ニューラルネットワークの入り口です。
ニューラルネットワークで予想するために
必要なパラメータ(特徴量)を受け取ります。
・出力層・・・ニューラルネットワークの出口です。
ニューラルネットワークで予想した結果を出力します。
・中間層・・・入力層と出力層をつなぐ層です。
入力層から渡されたデータを中間層のニューロン間で計算し、
その結果を次の中間層・あるいは出力層に渡します。
ディープラーニングで使用するニューラルネットワーク
(ディープニューラルネットワーク)ではこの中間層を複数層保有します。
ここまでがニューラルネットワークの概要と構成の説明です。
続いて、ニューラルネットワークの学習についても簡単に触れておきます。
ニューラルネットワークの学習について
ここからはニューラルネットワークの学習について説明いたします。
この学習結果がニューラルネットワークの出来に直結しますので、頑張りましょう!
ニューラルネットワークの学習は以下の手順で進めます。
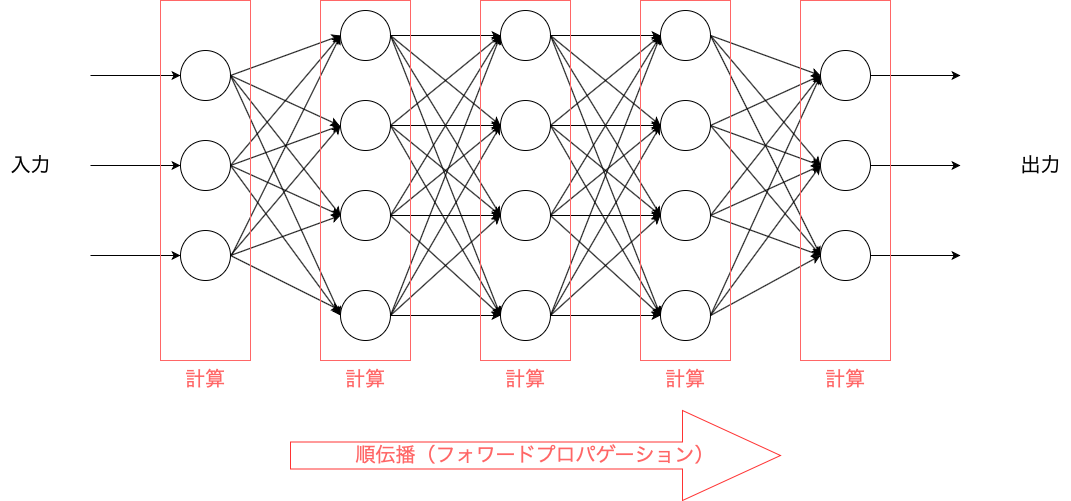
① 入力層で受け取った情報を中間層、出力層に順に伝えていく。
伝える過程で各層のユニットにて計算を行い、出力層にて予想結果を出力する。
これを順伝播(フォワードプロパゲーション)と言います。
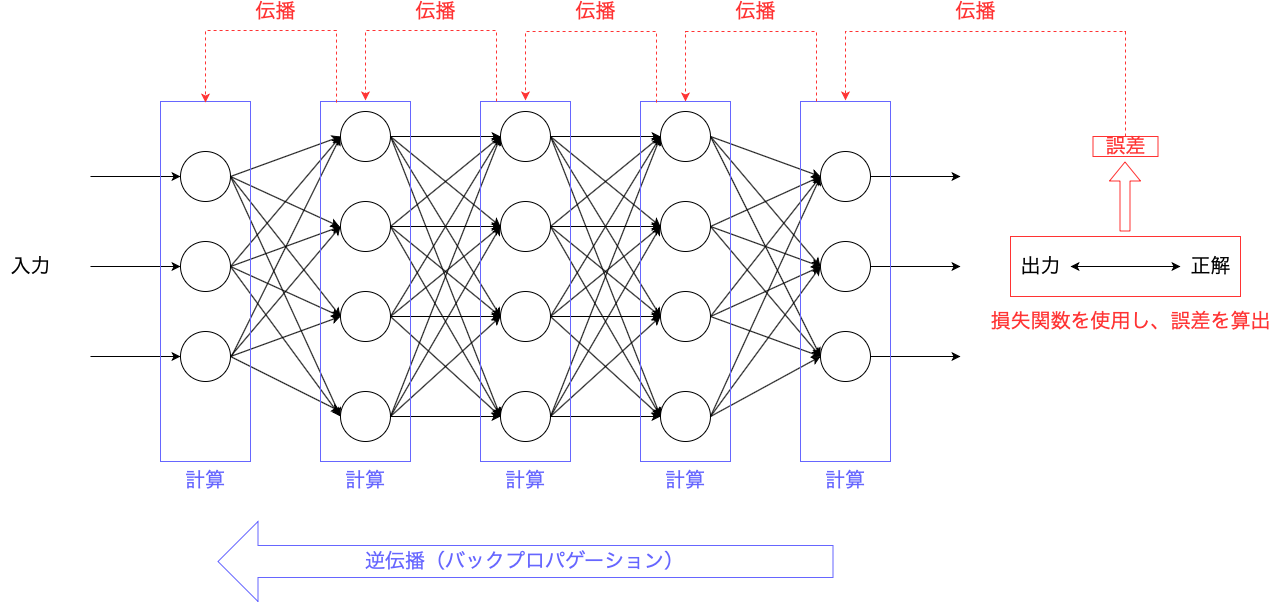
② 出力された予想結果と正解との誤差を損失関数にて算出し、
その誤差を出力層から入力層に逆に伝えていき、
各層のユニットの重み・バイアスを更新する。
これを逆伝播(バックプロパゲーション)と言います。
③ ①と②を繰り返し実施し、出力値と正解との誤差を小さくし、
予想精度をより高くなるように学習を行う。
ニューラルネットワークの学習については以上となります。
一応②で出てきた損失関数についても説明いたします。
・損失関数
損失関数は、ニューラルネットワークの出力値と正解との誤差を定義する関数です。
ニューラルネットワークの学習の目的は重み・バイアスを調整し、
出力値と正解との誤差を最小限にすることです。
この誤差を定義する損失関数として2種類紹介いたします。
・二乗和誤差
二乗和誤差は出力値と正解の差を二乗し、全ての出力層のユニットで総和をとった
ものです。
誤差をE、Ykを出力層の各出力値、Tkを正解値と定義すると
以下の式で表現されます。
E=\frac{1}{2}\sum_k(Y_{k}-T_{k})^{2}
二乗和誤差は回帰問題(例えば 過去の日経平均株価などを元に翌日の株価を予想する など)
でよく使用されます。
・交差エントロピー誤差
交差エントロピー誤差は出力値Ykの自然対数と正解Tkの積の総和を
マイナスしたものです。
E=-\sum_kT_{k}log(Y_{k})
こちらは分類問題(例えば キノコの色などを元に毒キノコか無毒キノコかを判別する など)
でよく使用されます。
ここまでがディープラーニング(どちらかというとニューラルネットワーク)の説明です。
続いて**Keras**の簡単な説明をいたします。
Kerasってそもそも何?
Kerasは,Pythonで書かれた,TensorFlowまたはCNTK,Theano上で実行可能な高水準のニューラルネットワークライブラリです。
Kerasは,迅速な実験を可能にすることに重点を置いて開発されました。
KerasはTensorFlowまたはCNTK,Theanoなどの機械学習ライブラリの
上位APIとしてつくられました。
Kerasを使うことで、以下の手順で簡単にニューラルネットワークを作成できます。
①とある問題を予想するためのモデルを定義する。(例えば、「競艇の一位を予測するモデル」)
②定義したモデルに入力層・中間層(隠れ層)・出力層 などの層(レイヤー)を追加する。
③モデルをコンパイルする。
④訓練データを使用してモデルの訓練を行う。
また、今回は触れませんが、同様の手順でCNNやRNNの作成も簡単にできます。
今回はTensorFlowをバックエンドとしてKerasを使っていきます。
Kerasの使い方
ここからはKerasの使い方を説明いたします。
前章で説明した手順①〜④の順に説明します。
手順①〜④の前にまずは必要なライブラリをインポートします。
import keras
from keras.models import Sequential
from keras.layers import Dense
①とある問題を予想するためのモデルを定義する。
モデルの定義については以下のどちらかの手法で行います。
・keras.models.Sequentiaクラスを使用する
・Function APIを使用する
どちらを使用しても問題ないですが、今回はSequentialクラスを使用します。
# モデル作成
model = Sequential()
②定義したモデルに入力層・中間層(隠れ層)・出力層 などの層(レイヤー)を追加する。
定義したモデルへ層を追加する際はaddメソッドを使用します。
# モデルに入力層を追加する
model.add(Dense([入力層のユニット数], input_shape=([訓練データの特徴数],), activation=[活性化関数]))
# モデルに中間層を追加する
model.add(Dense([中間層のユニット数], activation=[活性化関数]))
# モデルに出力層を追加する
model.add(Dense([出力層のユニット数], activation=[活性化関数]))
今回addメソッドで追加したものは以下の通り
・keras.layers.Denseクラス
こちらは全結合層を表すレイヤークラスです。
上述のニューラルネットワークのように各ユニットの出力が
次の層の全てのユニットの入力になるのが特徴です。
主な引数は以下の通り
・Units:層のユニット数
・input_shape:入力されるデータの形状を設定する
(何種類の特徴があるのか、訓練に使用するデータはいくつか)
input_shapeは入力層のみ設定する
・activation:使用する活性化関数を設定する。
③モデルをコンパイルする。
モデルへの層追加が完了した後に、モデルのコンパイルをcompileメソッドで実施します。
# モデルをコンパイルする
model.compile(loss=[損失関数], metrics=['accuracy'])
compileメソッドの引数は以下の通り
・loss:損失関数を設定する
損失関数はモデルの出力と正解との誤差がどれだけあるのか(勾配)を定義する。
損失関数の選び方は以下の2通り
1.回帰問題を解くためのニューラルネットワークの場合
平均二乗誤差(loss='mean_squared_error')を指定する
2.分類問題を解くためのニューラルネットワークの場合
2クラス分類の場合は交差エントロピー(loss='binary_crossentropy)を指定し、
多クラス分類(Kクラス)の場合は多クラス交差エントロピー
(loss='categorical_crossentropy’)を指定する
・metrics:評価関数を設定する
評価関数はモデルの出力の良し悪しを評価する
評価関数として使用することが多いのはaccuracy(正解率)
④訓練データを使用してモデルの訓練を行う
コンパイルが完了したのでいよいよモデルの訓練が始まります。
訓練するためにはfitメソッドを使用します。
# モデルを訓練する
model.fit([訓練データ], [訓練データの正解],
batch_size=[パラメータの更新タイミング],
verbose=[訓練の過程をコンソール出力するか?],
epochs=[訓練データ全てを何周するか])
fitメソッドの引数は以下の通り
・x:訓練データ(Numpy配列)
・y:訓練データの正解の値
・batch_size:訓練データを更新するタイミング(訓練データ数)
デフォルトは32
・verbose:訓練中の過程をコンソール出力するかを設定
0は出力しない
1はプログレスバーとして実行ごとにコンソール出力
2は1エポック毎にコンソール出力
・epochs:訓練データ全ての反復回数
例えば10を設定した場合は、訓練データ全ての実行を10回行う
これでモデルの作成・訓練は完了です。
最後に作成したモデルを使用して予想を行います。
予想はpredictメソッドを使用します。
# 作成・訓練したモデルで予想する
model.predict([予想したいデータ], batch_size=[バッチ処理のサイズ],
verbose=[コンソール出力するか?])
Kerasの使用方法については以上となります。
まとめ
ニューラルネットワークの説明とKerasの使い方について説明させていただきました。
しかし、私が説明した内容はニューラルネットワークとKerasのほんの一部でしかありません。
ですので、次の記事では実際にKerasを使用して競艇の予測をした話をしつつ、
ニューラルネットワークが抱える課題やそれを解決するためのKerasの使い方をご紹介する予定です。
最後に、今回私がディープラーニング・Kerasを学んだ際に
参考となった書籍をご紹介させていただきます。
参考文献
・はじめてのディープラーニング
=>これからディープラーニングを学ぶ方には是非読んでいただきたい一冊です。
こちらの本ではTensorFlowやKerasなどのディープラーニングでよく使用される
フレームワークを使わずにニューラルネットワークやディープニューラルネットワークを
構築しています。
ですので、フレームワークからは見えない内部の計算ロジックなどを基礎から学べます。
・東京大学のデータサイエンティスト育成講座
=>こちらは機械学習の各手法を学べる本です。
ですのでディープラーニングだけではなく、それ以外の機械学習の手法も学びたい方
にオススメです。
内容もPythonを使用して実際にコードを書いていきますので、理論と実装方法を
学べるため、一度読んで損はないはずです!
・PythonとKerasによるディープラーニング
=>こちらはKerasの開発者が作られた本です。
こちらの本はディープラーニングの理論ではなくKerasの使い方を説明していますので、
こちらの本を読まれる前にディープラーニングの理論を学んでいただきたいです。
しかし、Kerasの開発者ですので、Kerasの使い方についてはとてもわかりやすいです。