1. 鞍点とは
鞍点は勾配が0かつ、ある方向からは極小を、ある方向からは極大をとるような点を指します。機械学習におけるGANや、化学反応経路探索における遷移状態に代表されるように様々な分野で重要なテーマです。
GANは本物そっくりのデータを生成する生成器(generator)と、本物と生成されたデータを判別する判別器(discriminator)によって構成されています。生成器では極大を、判別器では極小をとるように学習します。
化学反応では、安定した種々の原料から、ポテンシャルエネルギー曲面上の鞍点を通り、より安定な化合物へと変化します。
本記事では勾配法を用いた鞍点探索を行います。この手法は簡単なモデルにおいては有効ですが、複雑なモデル(e.g. 量子化学等)ではやや不安定な挙動を示すため、改良出来次第追記します。
この記事に興味が面白かったらLGTM!をお願いします。
2. 鞍点の定義
鞍点を次のように記述します。目的関数を$y=f(\boldsymbol{x})$、$\boldsymbol{x}=(x_1,x_2,\cdots,x_n)^\rm{T}$、極小値に対応する単位ベクトルを$\boldsymbol{b}=(b_1,b_2,\cdots,b_n)^\rm{T}$、極大値に対応する単位ベクトルを$\boldsymbol{c}=(c_1,c_2,\cdots,c_n)^\rm{T}$と定義します。このとき$f$の勾配が$0$となり、かつ $y=f(\boldsymbol{x}+\boldsymbol{b}t)$が $t$に関して$t=0$で極小値をとり、$y=f(\boldsymbol{x}+\boldsymbol{c}t)$が $t$に関して$t=0$で極大値をとる点が鞍点です。数式で表すと次の通りです。
鞍点$\boldsymbol{x}=\boldsymbol{x}_0$において、
\left.\frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}}\right |_{\boldsymbol{x}=\boldsymbol{x}_0}= 0\\
\left.\frac{\partial^2 f(\boldsymbol{x}+\boldsymbol{b}t)}{\partial t^2}\right |_{\boldsymbol{x}=\boldsymbol{x}_0, t=0} > 0\\
\left.\frac{\partial^2 f(\boldsymbol{x}+\boldsymbol{c}t)}{\partial t^2}\right |_{\boldsymbol{x}=\boldsymbol{x}_0, t=0} < 0
が成立します。
例として $y=x_1^2-x_2^2$を考えます。$x_1=0$、$x_2=0$ において勾配が$0$になり、かつ $\boldsymbol{b}=(1, 0)^\rm{T}$において $y=(0+1 t)^2-(0+0 t)^2=t^2$は$t=0$で極小値をとり、 $\boldsymbol{c}=(0, 1)^\rm{T}$において $y=(0+0 t)^2-(0+1t)^2=-t^2$は$t=0$で極大値をとります。従ってこの点は鞍点であると推定できます。
3. 鞍点探索
この手法では初期化と探索の2過程をとります。初期化では適切な$\boldsymbol{b}$と$\boldsymbol{c}$の初期値を見つけます。探索では鞍点を勾配に従って探索します。
3.1 初期化
先述のとおり $\boldsymbol{b}$は極大値に、$\boldsymbol{c}$は極小値に対応します。まずは$y=f(\boldsymbol{x}+\boldsymbol{b}t)$の $t$に関する2階微分が最大になるような $\boldsymbol{b}$を決定します。簡単のために再急降下法による反復法を用います。数式で表すと次の通りです。
\mathrm{grad}\ \boldsymbol{b}_1 \leftarrow \frac{1}{\delta} \left( \nabla f \left(\boldsymbol{x}+\delta \boldsymbol{b} \right) - \nabla f \left(\boldsymbol{x}-\delta \boldsymbol{b} \right) \right)\\
\mathrm{grad}\ \boldsymbol{b}_2 \leftarrow \mathrm{grad}\ \boldsymbol{b}_1 - \left( \boldsymbol{b} \cdot \mathrm{grad}\ \boldsymbol{b}_1 \right)\boldsymbol{b}\\
\boldsymbol{b} \leftarrow \boldsymbol{b} + \epsilon_1 \ \mathrm{grad}\ \boldsymbol{b}_2\\
\boldsymbol{b} \leftarrow \frac{\boldsymbol{b}}{\mathrm{norm} \left(\boldsymbol{b}\right)}\\
微小量を$\delta$、学習率を$\epsilon_1$としました。第1式は$n$次元ユークリッド空間の基底に対する微分です。工夫として、勾配を利用できるように式変形を行いました。これをそのまま更新量とすると単位ベクトルである $\boldsymbol{b}$に対して適切ではないため、第2式で単位球面上に沿った $\boldsymbol{b}$の更新量に変換する必要があります。第3式は極大値に向かって更新、第4式では単位ベクトルにするため規格化します。
同様に$y=f(\boldsymbol{x}+\boldsymbol{c}t)$の $t$に関する2階微分が最大になるような $\boldsymbol{c}$を決定します。数式で表すと次の通りです。
\mathrm{grad}\ \boldsymbol{c}_1 \leftarrow \frac{1}{\delta} \left( \nabla f \left(\boldsymbol{x}+\delta \boldsymbol{c} \right) - \nabla f \left(\boldsymbol{x}-\delta \boldsymbol{c} \right) \right)\\
\mathrm{grad}\ \boldsymbol{c}_2 \leftarrow \mathrm{grad}\ \boldsymbol{c}_1 - \left( \boldsymbol{c} \cdot \mathrm{grad}\ \boldsymbol{c}_1 \right)\boldsymbol{c}\\
\boldsymbol{c} \leftarrow \boldsymbol{c} - \epsilon_1 \ \mathrm{grad}\ \boldsymbol{c}_2\\
\boldsymbol{c} \leftarrow \frac{\boldsymbol{c}}{\mathrm{norm} \left(\boldsymbol{c}\right)}
$\boldsymbol{b}$との相違点は第3式で極小値の方向に更新している点です。収束判定として$\mathrm{grad}\ \boldsymbol{b}_2$および$\mathrm{grad}\ \boldsymbol{c}_2$を用いることができます。
3.2 鞍点探索
探索は先ほどの$\mathrm{grad}\ \boldsymbol{b}_2$および $\mathrm{grad}\ \boldsymbol{c}_2$を用います。$-\mathrm{grad}\ \boldsymbol{b}_2$の方向には極小値が、 $\mathrm{grad}\ \boldsymbol{c}_2$の方向は極大値が存在するため、これに従って更新することで鞍点へ到達できます。数式で表すと次の通りです。
\boldsymbol{x} \leftarrow \boldsymbol{x} + \epsilon_2 \ \left( -\mathrm{grad}\ \boldsymbol{b}_2 +\mathrm{grad}\ \boldsymbol{c}_2 \right)
また$\boldsymbol{x}$の更新に従って $\mathrm{grad}\ \boldsymbol{b}_2$と $\mathrm{grad}\ \boldsymbol{c}_2$もまた変化しているため、初期化で行った $\boldsymbol{b}$と $\boldsymbol{c}$も同時に行う必要があります。
4. 実装
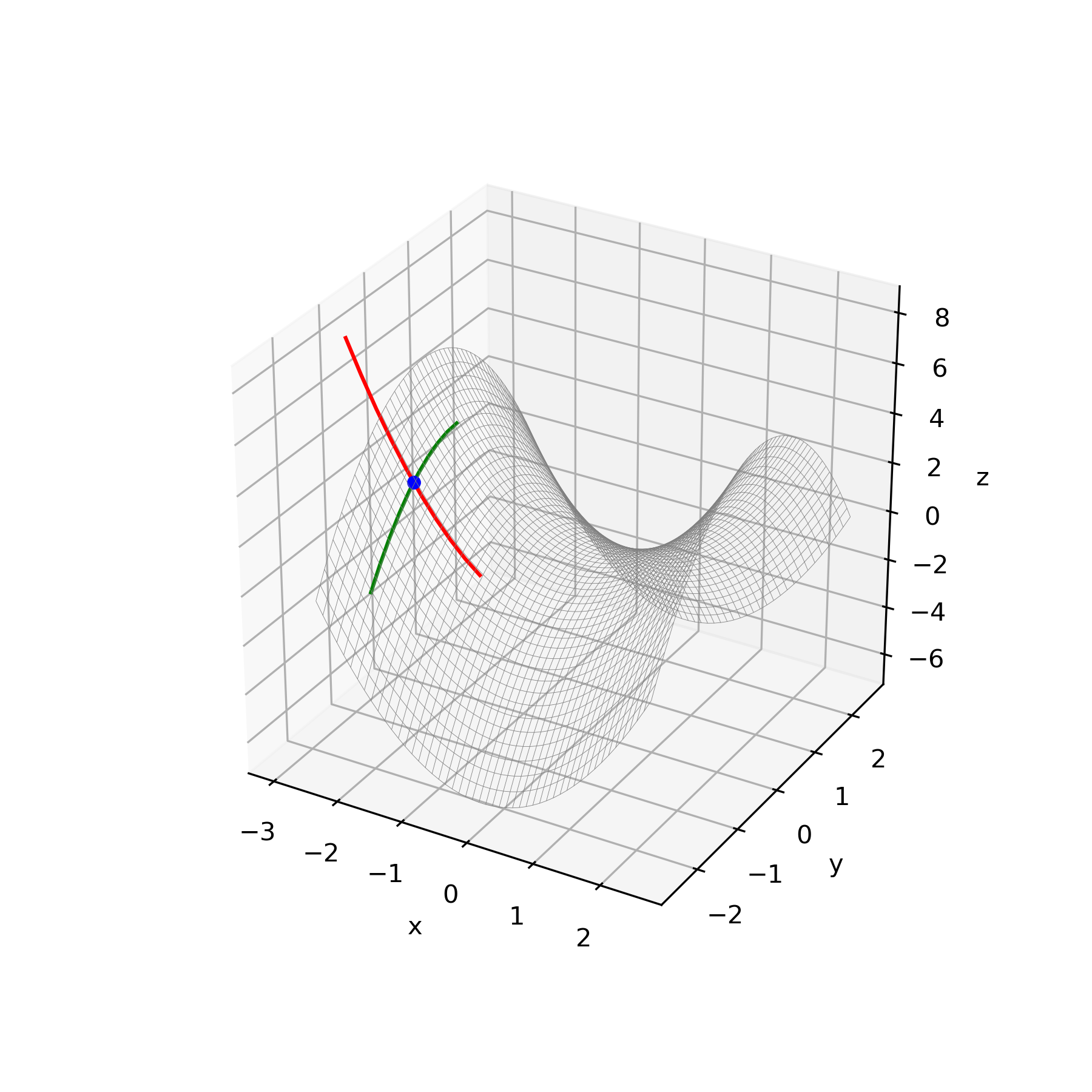
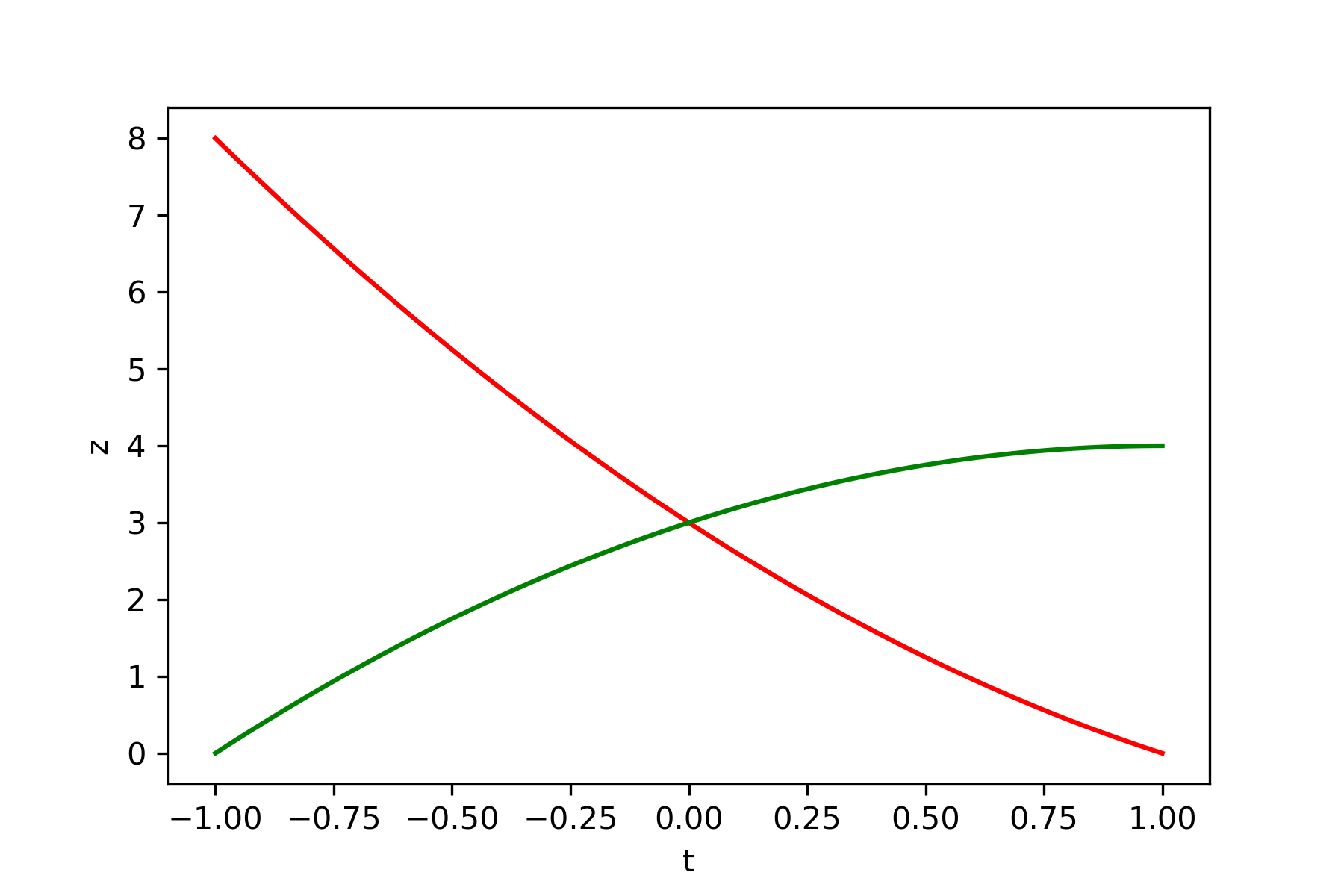
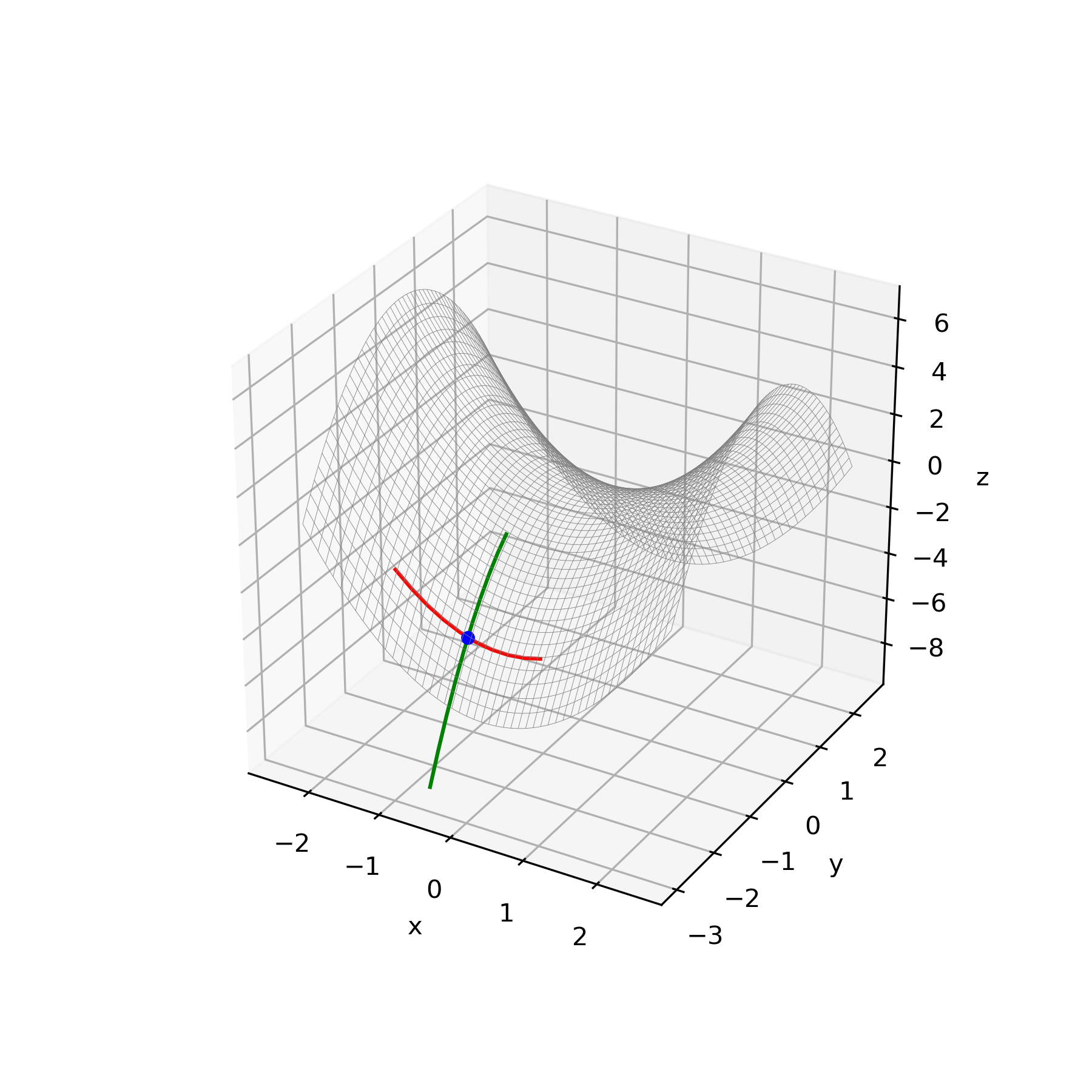
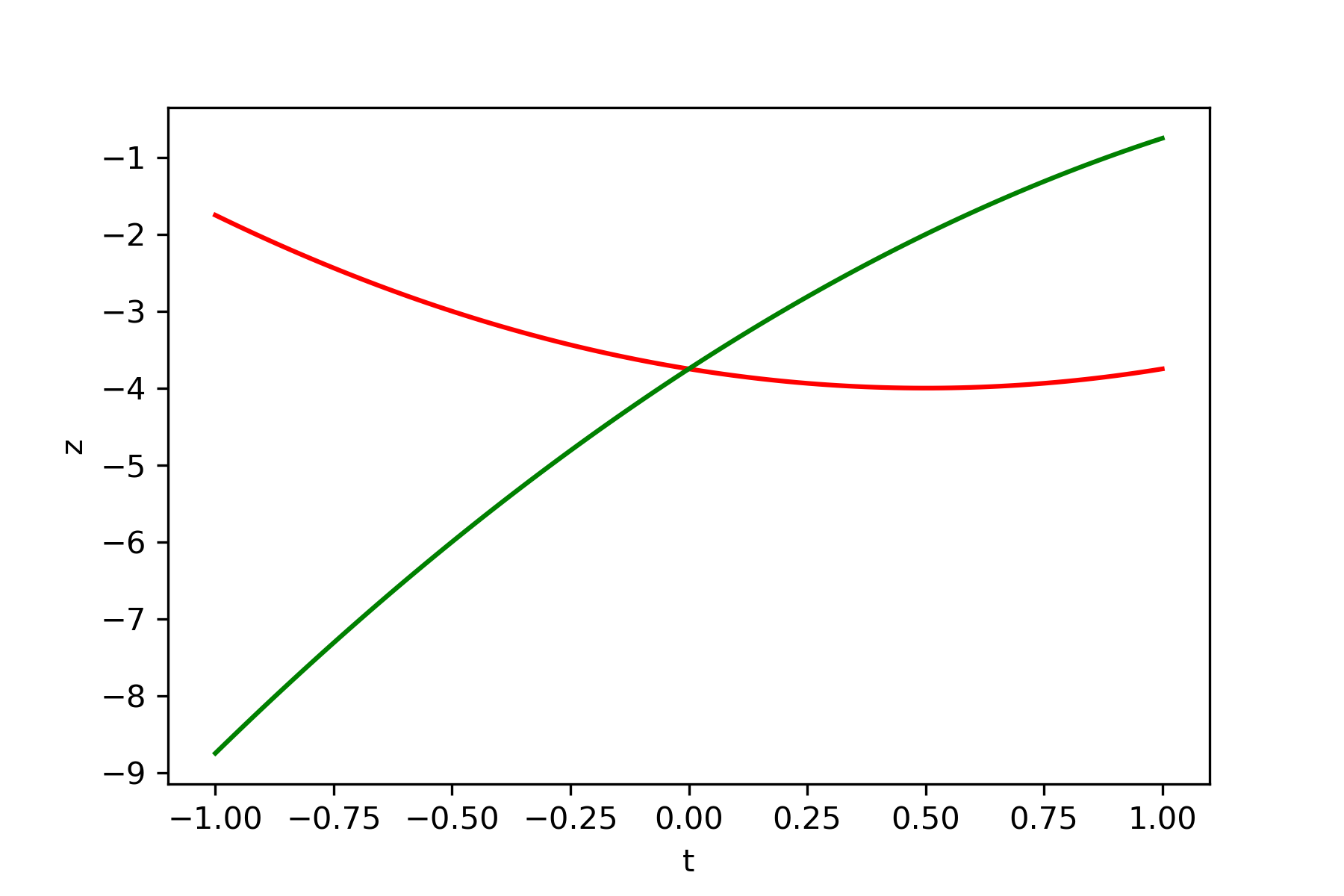
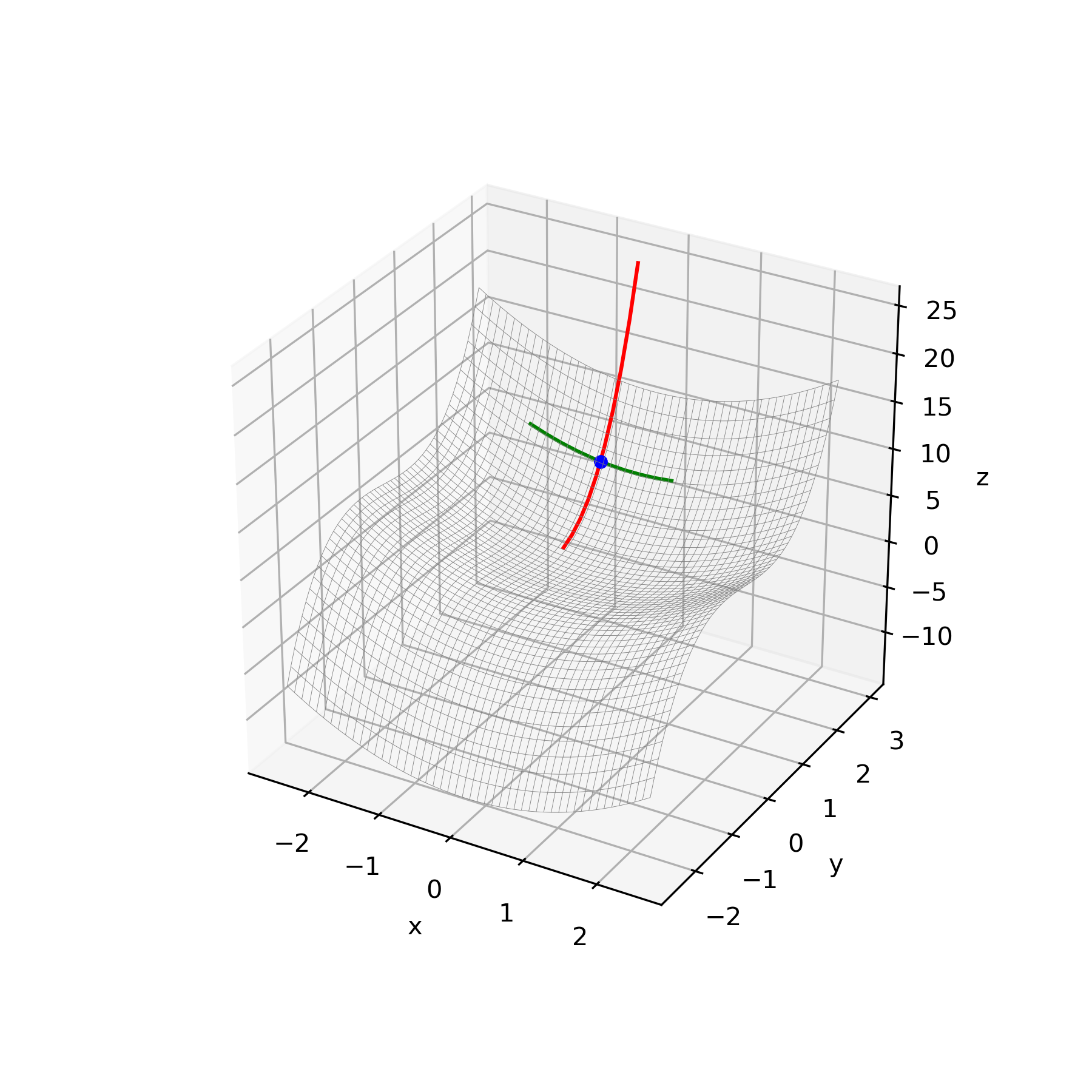
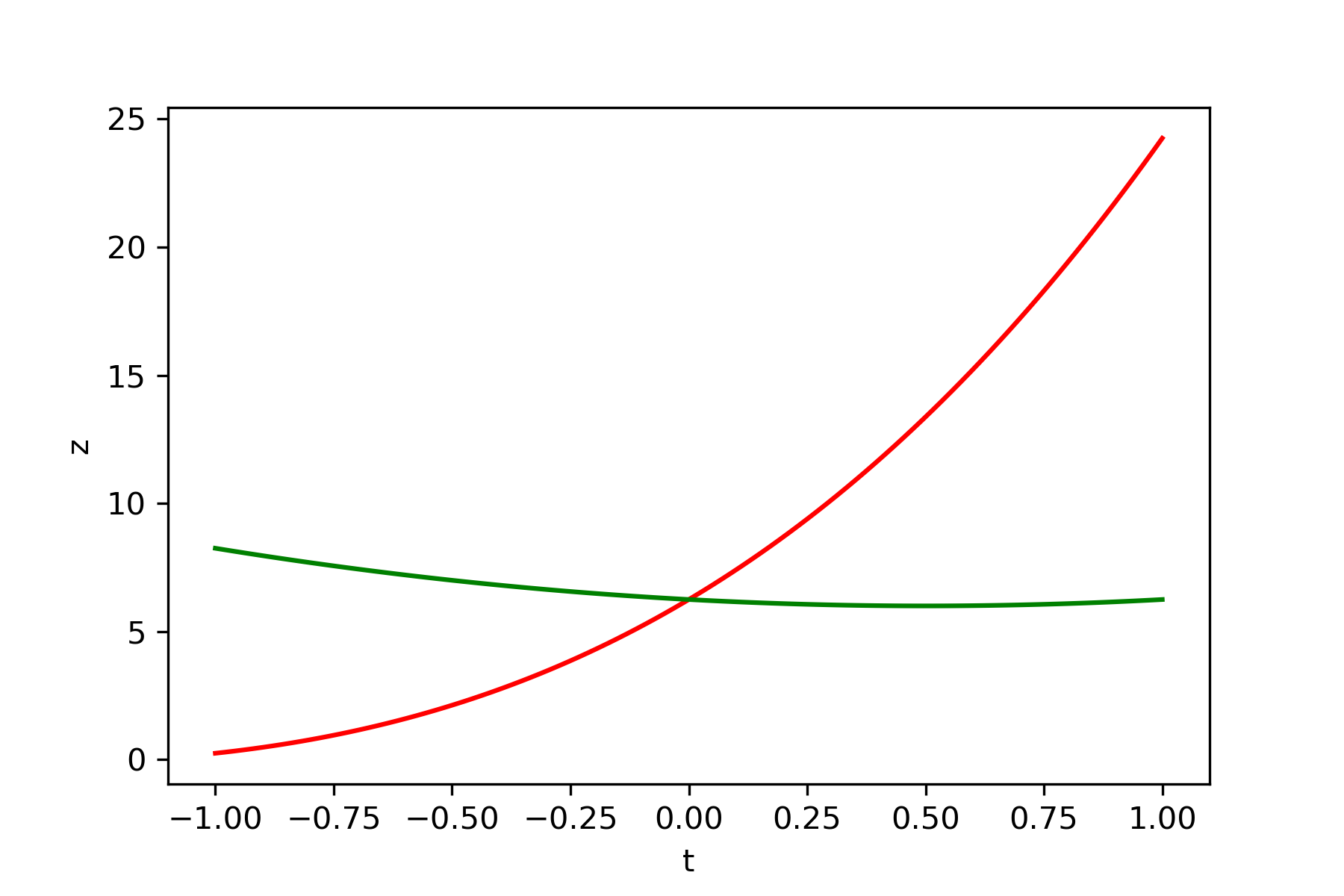
上記のアルゴリズムに従って種々の関数の鞍点を導出しました。更新方法は再急降下法を使用、Pythonにて実行しました。赤線が極小値ベクトル、緑線が極大値ベクトルです。
・関数 $y=x_1^2-x_2^2$
初期値$x_1=-2$、$x_2=-1$
微小量$\delta=0.001$
学習率$\epsilon_1=0.1$、$\epsilon_1=0.1$
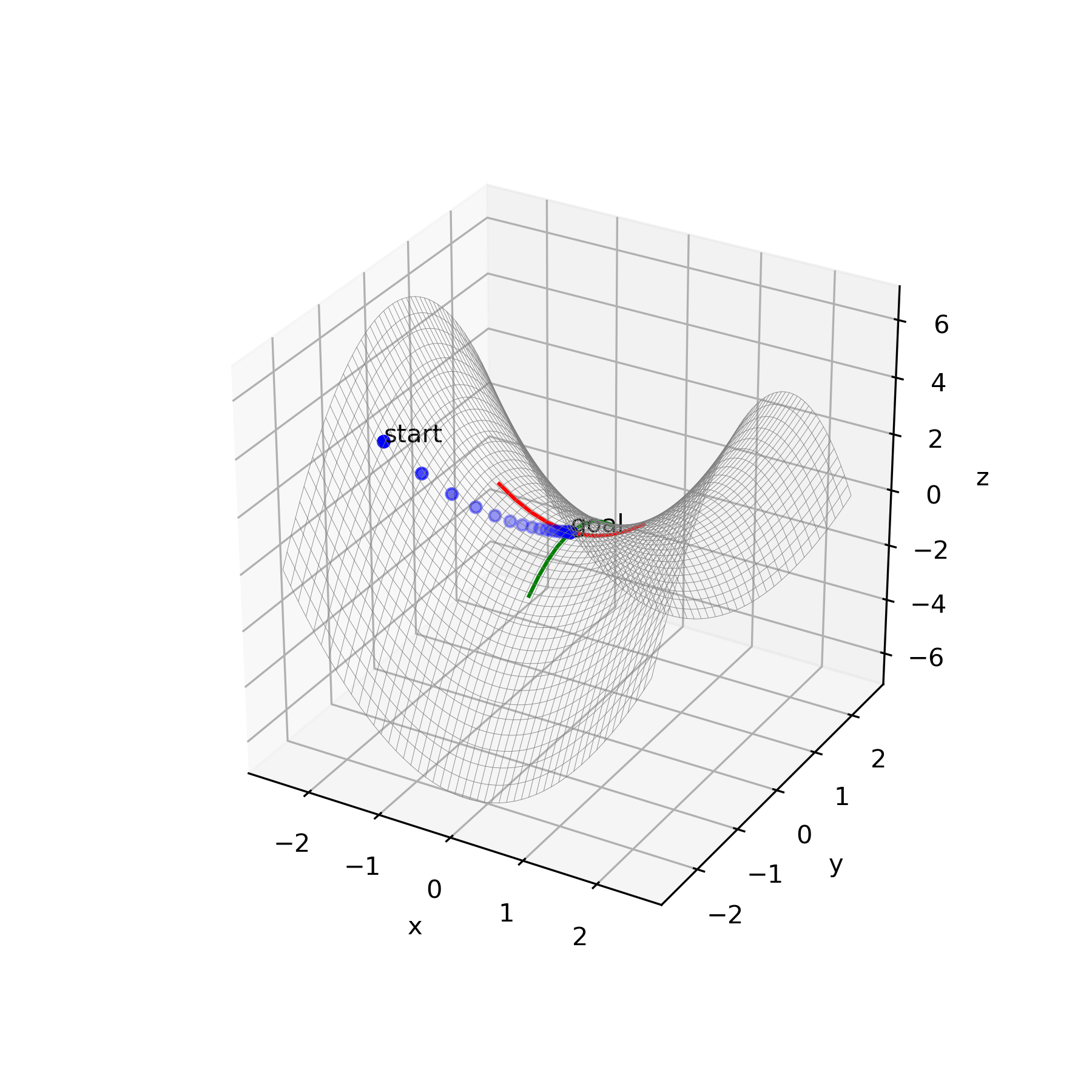
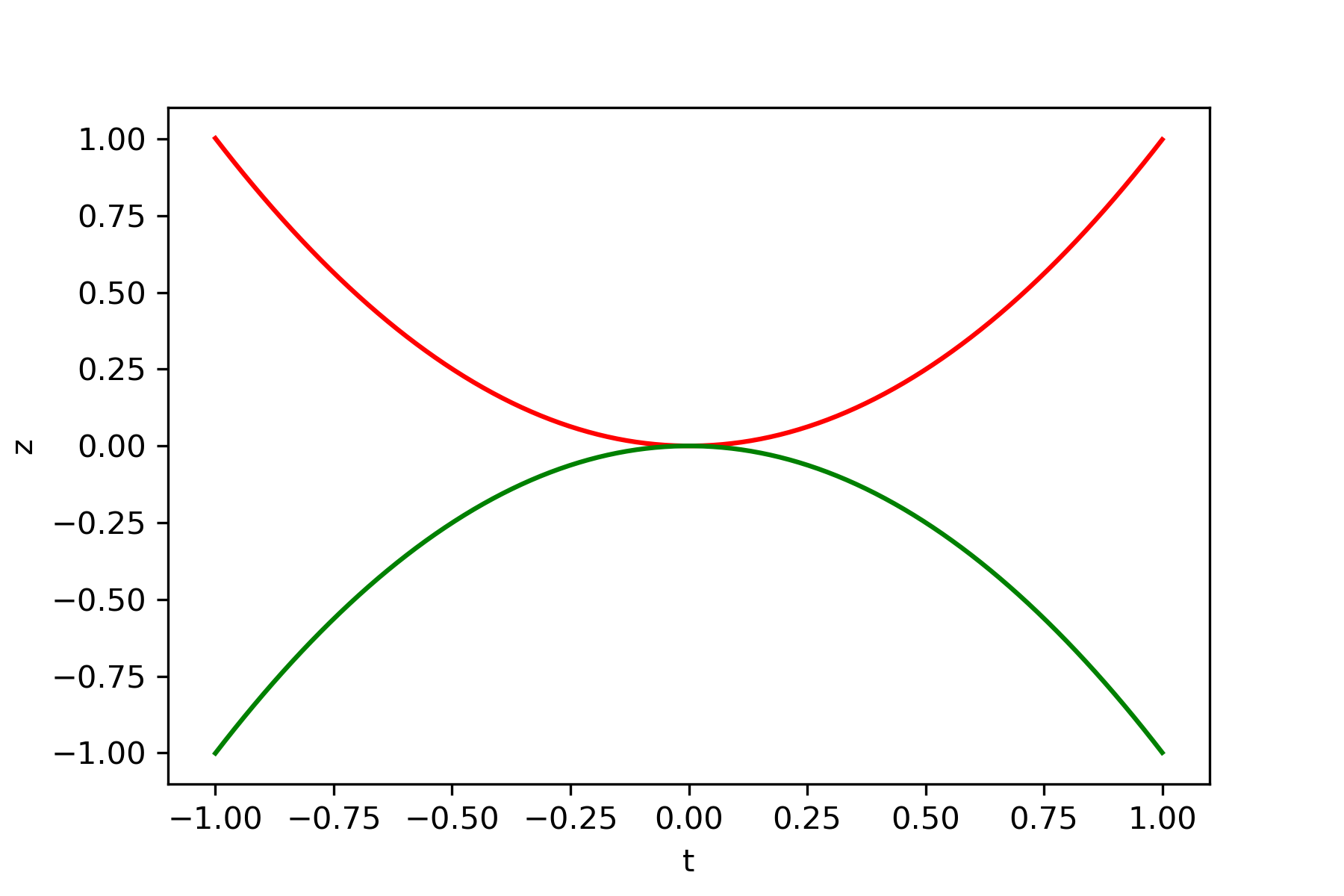
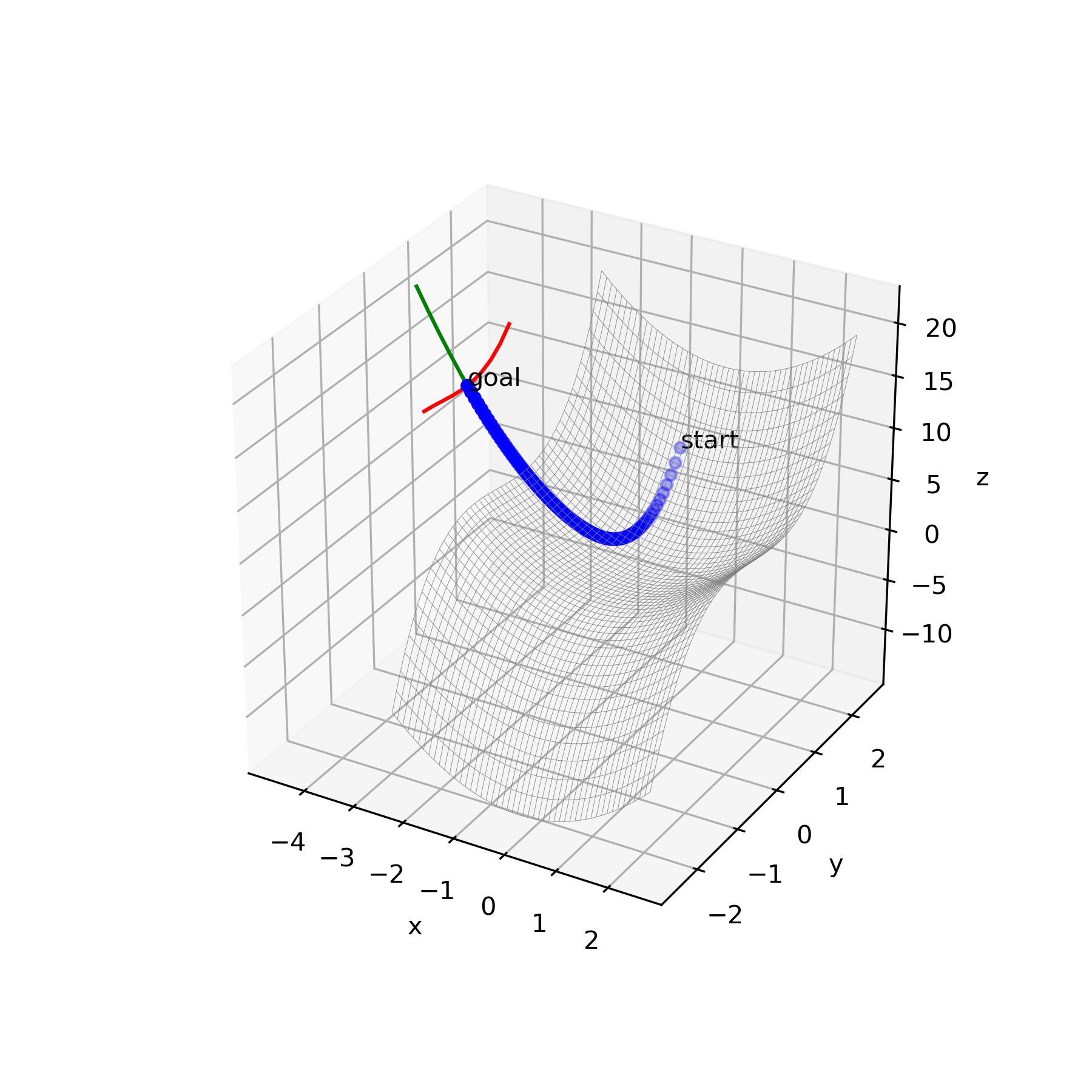
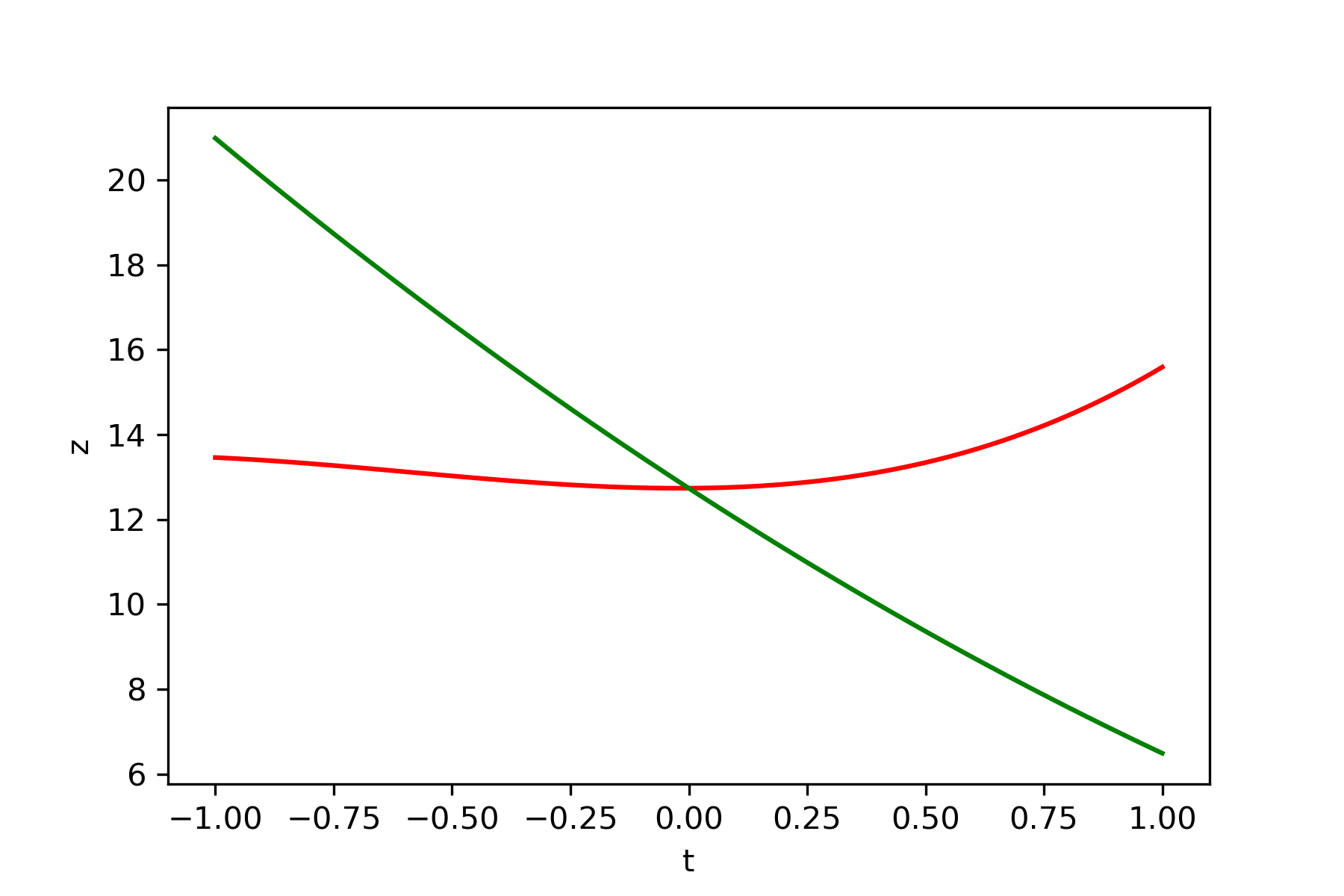
結果
鞍点$x_1=-0.0003$、$x_2=-0.001$
$\boldsymbol{b}=(1,0)^\rm{T}$、$\boldsymbol{c}=(0,1)^\rm{T}$
・関数 $y=x_1^2+x_2^3-x_2$
初期値$x_1=-2$、$x_2=-0.5$
微小量$\delta=0.05$
学習率$\epsilon_1=0.1$、$\epsilon_1=0.1$
結果
鞍点$x_1=-0.0011$、$x_2=-0.5774$
$\boldsymbol{b}=(1,0)^\rm{T}$、$\boldsymbol{c}=(0,1)^\rm{T}$
5. 課題
改善点として、勾配法なため、共役勾配法や機械学習における種々のオプティマイザ(e.g. Momentum、RMSProp、Adam、RAdam)およびwegstain法が利用可能です。
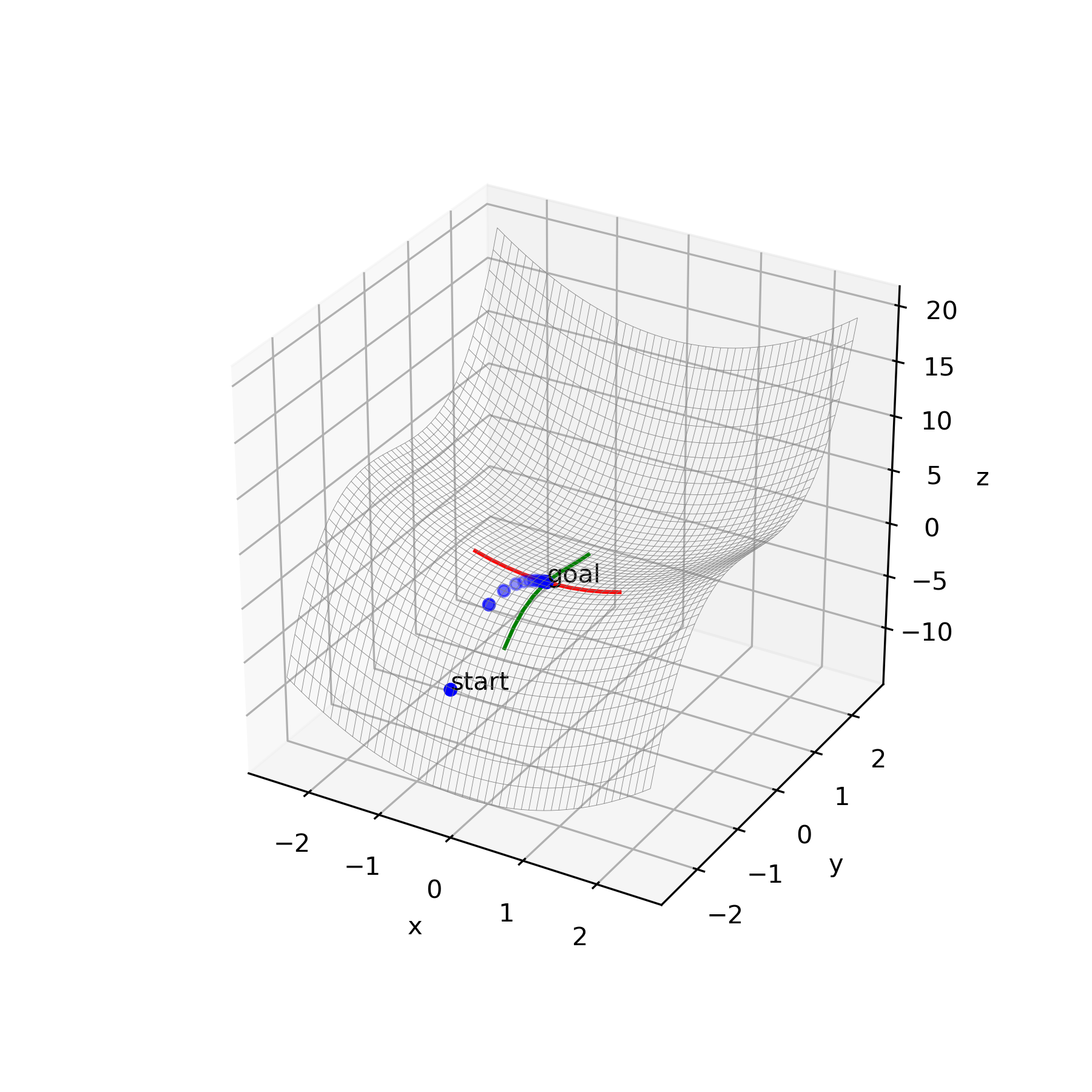
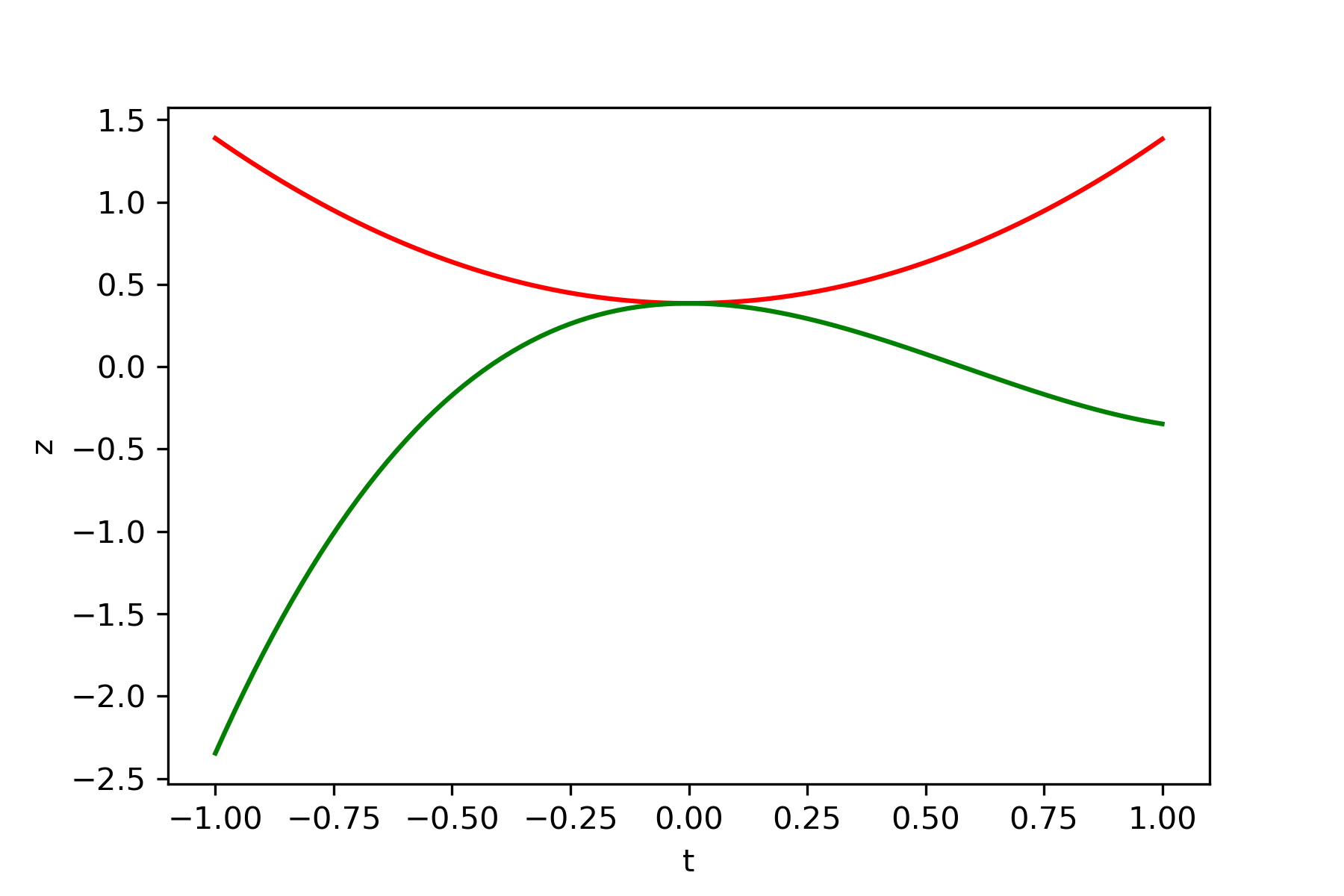
問題点として安定性が悪いことが考えられます。化学反応予測に利用できる鞍点探索に利用できるかと考えましたが、おかしな構造で収束してしまいました。また初期値によっては鞍点に収束しません。以下に例を示します。これは先ほどの例の初期値が異なるものです。
・関数 $y=x_1^2+x_2^3-x_2$
初期値$x_1=-2$、$x_2=-0.5$
微小量$\delta=0.05$
学習率$\epsilon_1=0.1$、$\epsilon_1=0.1$
この例では $x_2$の方向が極小値をとり、 $x_1$の向きが極大値をとるように $\boldsymbol{b}$および $\boldsymbol{c}$が更新されてしまっています。従って3次関数の極小値に向かって更新しつつ、2次関数の坂をぐんぐんと登っていってしまっています。
6. 結言
本記事では勾配法を用いた鞍点探索を行いました。視認性のため2変数関数の例を示しましたが、実際は任意変数関数を用いることができます。質問等がございましたらコメントにて返信いたします。式変形やソースコードのご要望がありましたらお気軽にコメントしてください。
7. ソースコード(2次関数)
「計算1 初期化」のところに関数や初期値、学習率等の設定があります。クラスSDGの内容を種々のオプティマイザに変更することができます。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from datetime import datetime
np.set_printoptions(precision=4, floatmode='maxprec')
class SDG:
def __init__(self, learning_rate):
self.learning_rate = learning_rate
def solve(self, coord, gradient):
return coord - self.learning_rate*gradient
class SaddlePoint:
def __init__(self, function, gradient, coordinate, delta=1.0e-3,
learning_rate=0.5, max_iteration=1000,
judgment1=1.0e-8, judgment2=1.0e-8, log_span=100):
"""
初期化コンストラクタ
function --目的関数
differential --関数の1階微分
coordinates --初期座標
delta --微小値
learning_rate --学習率
judgment --収束判定1
judgment --収束判定2
log_span --ログの表示間隔
"""
self.function = function
self.gradient = gradient
self.coordinate = coordinate.copy()
self.dim = len(coordinate)
self.delta = delta
self.learning_rate = learning_rate
self.max_iteration = max_iteration
self.judgment1 = judgment1
self.judgment2 = judgment2
self.log_span = log_span
# 基底ベクトル
self.b = np.random.rand(self.dim)
self.b /= np.linalg.norm(self.b)
self.c = np.random.rand(self.dim)
self.c /= np.linalg.norm(self.c)
# SDG
self.sdg_b_init = SDG(learning_rate)
self.sdg_c_init = SDG(learning_rate)
self.sdg_b_solv = SDG(learning_rate)
self.sdg_c_solv = SDG(learning_rate)
self.sdg_a_solv = SDG(learning_rate)
def initialize(self):
"""
初期化する関数。適切なb,cを決定する
返り値 --極小値方向ベクトルb, 極大値方向ベクトルc
"""
# 勾配
gradient = self.gradient
# 座標b
coordinate = self.coordinate
# 基底ベクトル
b = self.b.copy()
c = self.c.copy()
# 更新量
diff_b = np.zeros_like(b)
diff_c = np.zeros_like(c)
# 学習率
learning_rate = self.learning_rate
# 微小値
delta = self.delta
# 規格化
norm = np.linalg.norm
# 判定
judgement1 = self.judgment1
# ログ間隔
log_span = self.log_span
# SDG
sdg_b = self.sdg_b_init
sdg_c = self.sdg_c_init
z, _ = gradient(coordinate)
print("-----Initialization of b has started.-----")
for i in range(self.max_iteration):
# 1階微分
z_b1, grad_b1 = gradient(coordinate + delta*b)
z_b2, grad_b2 = gradient(coordinate - delta*b)
# 変化量計算
nabla_b = (grad_b1 - grad_b2)/delta
grad_b = nabla_b - (np.dot(b, nabla_b))*b
# 更新
b = sdg_b.solve(b, -grad_b)
# 規格化
b /= norm(b)
# 収束判定
error = np.linalg.norm(grad_b)
if i%log_span == 0:
print("Iteration = {}, Error = {}".format(i, error))
if error < judgement1:
print("Converged! Iteration = {}, Error = {}".format(i, error))
break
self.b = b.copy()
print()
print("-----Initialization of c has started.-----")
for i in range(self.max_iteration):
# 勾配計算
z_c1, grad_c1 = gradient(coordinate + delta*c)
z_c2, grad_c2 = gradient(coordinate - delta*c)
# 変化量計算
nabla_c = (grad_c1 - grad_c2)/delta
grad_c = nabla_c - (np.dot(c, nabla_c))*c
# 更新
c = sdg_c.solve(c, grad_c)
# 規格化
c /= norm(c)
# 収束判定
error = np.linalg.norm(grad_c)
if i%log_span == 0:
print("Iteration = {}, Error = {}".format(i, error))
if error < judgement1:
print("Converged! Iteration = {}, Error = {}".format(i, error))
break
self.c = c.copy()
print()
print("Result")
print("b = {}".format(self.b))
print("c = {}".format(self.c))
print()
return self.b, self.c
def solve(self):
"""
鞍点を探索する
返り値 --鞍点座標coordinate, 極小値方向ベクトルb, 極大値方向ベクトルc
"""
# 勾配
gradient = self.gradient
# 座標、座標をまとめたもの
coordinate = self.coordinate.copy()
coordinate_Array = coordinate.copy()
# 基底ベクトル
b = self.b.copy()
c = self.c.copy()
# 更新量
diff_b = np.zeros_like(b)
diff_c = np.zeros_like(c)
# 学習率
learning_rate = self.learning_rate
# 微小値
delta = self.delta
# 規格化
norm = np.linalg.norm
# 判定
judgement1 = self.judgment1
judgement2 = self.judgment2
# ログ間隔
log_span = self.log_span
# SDG
sdg_a = self.sdg_a_solv
sdg_b = self.sdg_b_solv
sdg_c = self.sdg_c_solv
print("-----Saddle-point solver has started.-----")
for i in range(self.max_iteration):
# 1階微分
z_b1, grad_b1 = gradient(coordinate + delta*b)
z_b2, grad_b2 = gradient(coordinate - delta*b)
z_c1, grad_c1 = gradient(coordinate + delta*c)
z_c2, grad_c2 = gradient(coordinate - delta*c)
grad_through_b = (z_b1-z_b2) / (2.0*delta)
grad_through_c = (z_c1-z_c2) / (2.0*delta)
# 2階微分
z, _ = gradient(coordinate)
grad2_through_b = (z_b1-2.0*z+z_b2) / delta**2.0
grad2_through_c = (z_c1-2.0*z+z_c2) / delta**2.0
# 更新
# coordinate = sdg_a.solve(coordinate,
# grad_through_b*b/(np.linalg.norm(grad_through_b)+np.linalg.norm(grad2_through_b))
# -grad_through_c*c/(np.linalg.norm(grad_through_c)+np.linalg.norm(grad2_through_c)))
coordinate = sdg_a.solve(coordinate, grad_through_b*b - grad_through_c*c)
coordinate_Array = np.vstack([coordinate_Array, coordinate])
# 収束判定
error_coordinate = np.linalg.norm(grad_through_b**2 + grad_through_c**2)
# b,cの更新
nabla_b = -(grad_b1 - grad_b2)/delta
grad_b = nabla_b - (np.dot(b, nabla_b))*b
# 更新
b = sdg_b.solve(b, grad_b)
# 規格化
b /= norm(b)
# 収束判定
error_b = np.linalg.norm(grad_b)
nabla_c = (grad_c1 - grad_c2)/delta
grad_c = nabla_c - (np.dot(c, nabla_c))*c
# 更新
c = sdg_c.solve(c, grad_c)
# 規格化
c /= norm(c)
# 収束判定
error_c = np.linalg.norm(grad_c)
if i%log_span == 0:
print("B converged! Iteration = {}, Error = {}".format(i, error_b))
print("C converged! Iteration = {}, Error = {}".format(i, error_c))
print("Iteration = {}, Error = {}".format(i, error_coordinate))
print()
if error_coordinate < judgement2:
print("Converged! Iteration = {}, Error = {}".format(i, error_coordinate))
break
self.coordinate = coordinate.copy()
self.b = b.copy()
self.c = c.copy()
print()
print("Result")
print("coordinate = {}".format(self.coordinate))
print("b = {}".format(self.b))
print("c = {}".format(self.c))
print()
return self.coordinate, coordinate_Array, self.b, self.c
# =============================================================================
# 計算1 初期化
# =============================================================================
def f(x):
# 関数
return x[0]**2 - x[1]**2
def gradient_f(x):
# 関数の1階微分
return f(x), np.array([2*x[0], -2*x[1]])
x_init = np.array([-2.0, -1.0], dtype="float")
saddlePoint = SaddlePoint(f, gradient_f, x_init, delta=1e-3,
learning_rate=0.1, max_iteration=100,
judgment1=1.0e-5, judgment2=1.0e-5, log_span=1)
b, c = saddlePoint.initialize() # 初期化
# =============================================================================
# グラフ描画 (2D)
# =============================================================================
t = np.linspace(-1.0, 1.0, 100)
tb = np.linspace(x_init-1.0*b, x_init+1.0*b, 100)
tc = np.linspace(x_init-1.0*c, x_init+1.0*c, 100)
fb = f(tb.T)
fc = f(tc.T)
plt.xlabel("t")
plt.ylabel("z")
plt.plot(t, fb, c="red")
plt.plot(t, fc, c="green")
plt.savefig("file/" + str(datetime.now().strftime("%Y_%m_%d_%H_%M_%S")) + "_2d1.png", dpi=300)
plt.show()
# =============================================================================
# グラフ描画 (3D)
# =============================================================================
# ワイヤーフレーム
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
X = np.linspace(-2.5, 2.5, 50)
Y = np.linspace(-2.5, 2.5, 50)
X, Y = np.meshgrid(X, Y)
Z = f([X,Y])
# 基底ベクトル
width = 1.0
bt = np.linspace(x_init-width*b,x_init+width*b,10)
bz = f(bt.T)
ct = np.linspace(x_init-width*c,x_init+width*c,10)
cz = f(ct.T)
# 軌跡
zArray = f(x_init)
# 表示
ax.plot_wireframe(X,Y,Z,color="gray",linewidth=0.2) # ワイヤーフレーム
ax.plot(bt[:,0],bt[:,1],bz,color="red") # 極小
ax.plot(ct[:,0],ct[:,1],cz,color="green") # 極大
ax.scatter(x_init[0],x_init[1],f(x_init),color="blue") # 軌跡
plt.savefig("file/" + str(datetime.now().strftime("%Y_%m_%d_%H_%M_%S")) + "_3d1.png", dpi=300)
plt.show()
# =============================================================================
# 計算2 鞍点探索
# =============================================================================
x, xArray, b, c = saddlePoint.solve() # 鞍点計算
# =============================================================================
# グラフ描画 (2D)
# =============================================================================
t = np.linspace(-1.0, 1.0, 100)
tb = np.linspace(x-1.0*b, x+1.0*b, 100)
tc = np.linspace(x-1.0*c, x+1.0*c, 100)
fb = f(tb.T)
fc = f(tc.T)
plt.xlabel("t")
plt.ylabel("z")
plt.plot(t, fb, c="red")
plt.plot(t, fc, c="green")
plt.savefig("file/" + str(datetime.now().strftime("%Y_%m_%d_%H_%M_%S")) + "_2d2.png", dpi=300)
plt.show()
# =============================================================================
# グラフ描画 (2D)
# =============================================================================
# ワイヤーフレーム
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
X = np.linspace(-2.5, 2.5, 50)
Y = np.linspace(-2.5, 2.5, 50)
X, Y = np.meshgrid(X, Y)
Z = f([X,Y])
# 基底ベクトル
width = 1.0
bt = np.linspace(x-width*b,x+width*b,10)
bz = f(bt.T)
ct = np.linspace(x-width*c,x+width*c,10)
cz = f(ct.T)
# 軌跡
zArray = f(xArray.T)
# 表示
ax.plot_wireframe(X,Y,Z,color="gray",linewidth=0.2) # ワイヤーフレーム
ax.plot(bt[:,0],bt[:,1],bz,color="red") # 極小
ax.plot(ct[:,0],ct[:,1],cz,color="green") # 極大
ax.scatter(xArray[:,0],xArray[:,1],zArray,color="blue") # 軌跡
ax.text(xArray[0,0],xArray[0,1],zArray[0], "start")
ax.text(xArray[-1,0],xArray[-1,1],zArray[-1], "goal")
plt.savefig("file/" + str(datetime.now().strftime("%Y_%m_%d_%H_%M_%S")) + "_3d2.png", dpi=300)
plt.show()