合意制御系の接続構造を推定しよう

はじめに

本記事は数理最適化 Advent Calendar 2025の11日目の記事になります。

過去にやったことの備忘録として、"Sparse Topology Estimation for Consensus Network Systems via Minimax Concave Penalty"について、簡潔に解説していきたいと思います。

ちなみに、シミュレーションのMATLABソースコードも公開しております。気になる方は、以下からどうぞ。

ただ、査読時に「ソースコードは公開しないの？」と聞かれて公開したため、人に見せられるコードではないです。後ほど綺麗に整備していきます。

なお、シミュレーションの実行にはCVXが必要となるので、試す際はCVXをインストールしてから動かしてください。

[2025.12.13 追記]
記述ミスがあったので修正しました．

この論文は何だ

簡単に言うと、「合意ネットワークの出力からどんな感じで繋がっているのかを推定しよう」という論文です。

本研究では、Maximum Likelihood Estimation（MLE: 最尤推定法）を用いてネットワークの繋がり方を推定するフレームワークに基づいて、最適化問題の定式化を行っています。これはつまり、観測されたデータに基づいて「観測された動きを最もうまく説明できるつながりは何だ？」というのを逆算していくのです。
最も一般的なアプローチとしては、データが多変量正規分布に従うと仮定する Gauss Graphical Model (GGM) が挙げられます。データが正規分布に従う場合、ネットワーク構造は分散共分散行列の逆行列である精度行列に直接出てくるわけです（行列行列うるさい）。そのため、「観測データから精度行列を推定する問題」として定式化することが可能です。
このとき、最小化すべき尤度関数は次のようになります¹。

\begin{align*}
\underset{\Lambda \succ 0}{\mathrm{minimize}} \quad -\log \det (\Lambda) + \mathrm{Tr}(S\Lambda) + \lambda\|\Lambda\|_1
\end{align*}

ここで、$S$はサンプリングしたデータから生成する標本共分散行列、$\Lambda$は精度行列、$\lambda>0$は正則化パラメータであり、$\lVert \ \cdot \ \rVert_1$は行列の$\ell^1$ノルムを表しています。この$\ell^1$ノルムのおかげで、推定されるパラメータの多くがゼロとなり、変数間の本質的な依存関係を抽出することが可能となるわけです。
なお、各項は次のようになっています。

• $-\log\det(\Lambda)$：精度行列の「広がり」を抑えつつ正定値性を保つ項

• $\mathrm{Tr}(S\Lambda)$：観測された共分散$S$と合うようにするデータフィットの項

• $\lambda|\Lambda|_1$：不要なエッジの重みをゼロにして、グラフ構造をスパースにする項

なぜスパース正則化項がついてる？

純粋なMLEだと、ノイズの影響ですべてノードが微小なつながりを持っているような推定結果を返して来ることが多いです。しかし、実際には繋がりがスパースとなることが多く、余計なエッジまで繋がっている判定してしまうわけですね。そこで、ペナルティ項（正則化項）として$\ell^1$ノルムを加えることで、「繋がりをなるだけ疎にしてくれ」という制約を加えるわけですね。このことから、別名Graphical Lassoと呼ばれたりします。

今回は最小化問題として定式化していますが、多くの文献では最大化問題として書かれていた記憶があったりなかったり。ただ、同じ凸最適化問題なので気にしない。

問題設定

さてさて、ここまでは一般的な Gauss Graphical Model(GGM) の話でした。では、本論文のターゲットである合意ネットワークではどうなるのか。そのために、まずは合意ネットワークのモデルを説明していきます。

次に示す、無向かつ非負の重みをもつ連続時間系における合意ネットワークについて考えます。

\dot{\boldsymbol{\psi}}(t) = -L_\boldsymbol{q}\,\boldsymbol{\psi}(t) + \boldsymbol{d}(t),

ここで、$\boldsymbol{\psi}(t) \in \mathbb{R}^n$はネットワークの状態変数、$\boldsymbol{d}(t) \in \mathbb{R}^n$はプロセスノイズを意味します。$\boldsymbol{q} \in \mathbb{R}_+^m$は全ノード間の通信リンクに割り当てられた重みであり、次元数は$m=n(n-1)/2$となります。

$L_{\boldsymbol{q}} \in \mathbb{R}^{n \times n}$は重み付きグラフラプラシアンであり、$L_{\boldsymbol{q}} = E \ \text{diag}(\boldsymbol{q}) \ E^{\top}$と表現することができます。行列$E \in \mathbb{R}^{n \times m}$は接続行列を意味しており、各列ベクトルは基底ベクトル$\boldsymbol{e}_i$を用いて$\boldsymbol{e}_i - \boldsymbol{e}_j, \ i<j$と表現できます。

わかりづらい　人向け、接続行列について簡単な例を示すと。$L_\boldsymbol{q} \in \mathbb{R}^{4 \times 4}$のグラフラプラシアンの場合、接続行列$E \in \mathbb{R}^{4 \times 6}$は次のようになります。

\begin{align*}
E =
\begin{bmatrix}
1 & 1 & 1 & 0 & 0 & 0\\
-1 & 0 & 0 & 1 & 1 & 0\\
0 & -1 & 0 & -1 & 0 & 1\\
0 & 0 & -1 & 0 & -1 & -1\\
\end{bmatrix}
\end{align*}

また、ノイズ$\boldsymbol{d}(t)$はガウス分布に従う白色ノイズで、以下に示す性質を満たします。

\begin{align*}
\mathbb{E}[\boldsymbol{d}(t)] = \boldsymbol{0}, 
\quad
\mathbb{E}[\boldsymbol{d}(t)\boldsymbol{d}(\tau)^{\top}] = \sigma^{2} I \delta(t - \tau), 
\quad
\mathbb{E}[\boldsymbol{\psi}(t)\boldsymbol{d}(\tau)^{\top}] = \boldsymbol{0},
\quad
\forall t, \tau \geq 0
\end{align*}

このネットワークに対して、最尤推定を用いて精度行列を求め、ネットワークがどんな感じでつながっているのかを推定する問題を考えます。

なお、合意ネットワークに興味がわいた人や「なんやそれ説明せんかい」って人は、以前に書いた記事がありますのでそちらをどうぞ。
初めての合意制御（連続時間系） - Qiita

コントリビューション

では、この論文では何をしたのかという話ですが。合意ネットワークと白色ノイズの性質を用いて、最尤推定のための最適化問題の定式化を行いました。加えて、ペナルティ項、求解アルゴリズムの再検討も行いました。

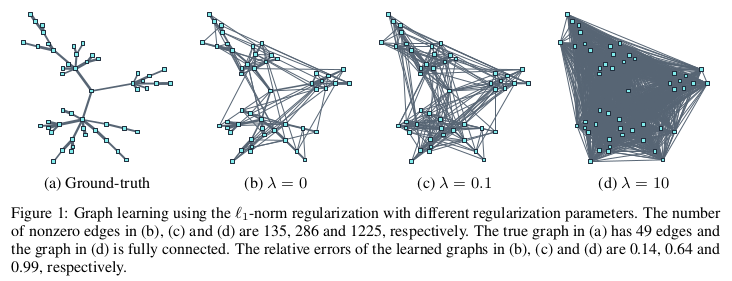
これはつまりどういうことか。上述したフレームワークで使用している$\ell^1$ノルムには実は欠点があります。それは、$\ell^1$ノルムのパラメータを大きくしすぎると、すべてのエッジの重さを小さい正数であると推定しまうのです²。$\ell^1$ノルムのような凸ペナルティを伴う正則化手法は、オラクル特性（漸近正規性および選択一貫性）を満たさないため、偏りのない推定を行うことが難しいです。

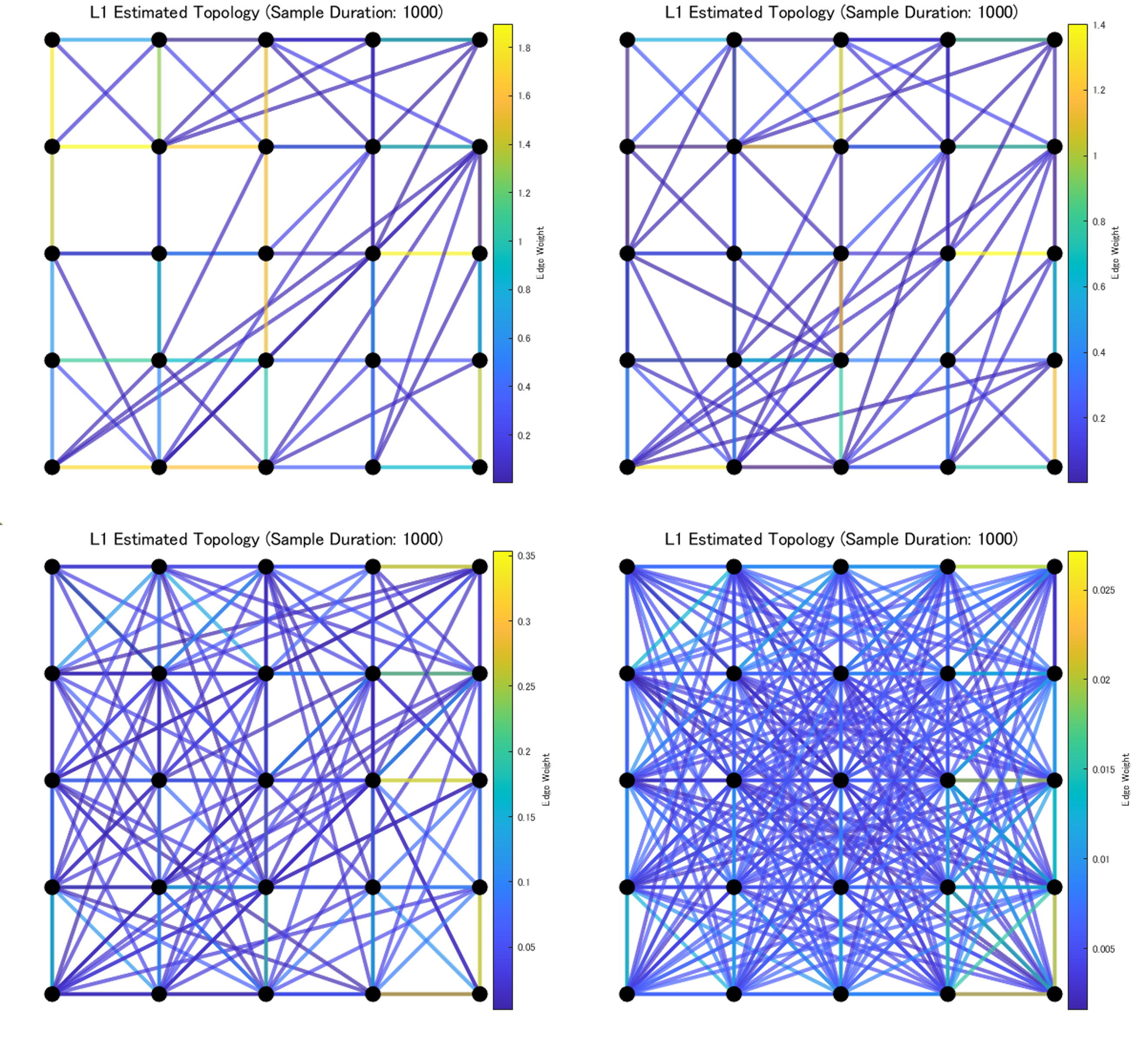
実際に見てみましょう。25個のノードを有するネットワークを用意しました。

左上$\lambda=0.0$、右上$\lambda=0.1$、左下$\lambda=1.0$、右下$\lambda=10.0$の結果になっています。図が小さくて見にくいかもしれませんが、ノードの重さがどんどん圧縮されていき、最終的には全ノードが存在する判定になっていますね。

このことから、最近では非凸なペナルティ関数を用いた研究が信号処理や画像処理で盛んに行われており³、その中でも MCP (Minimax Concave Penalty) を用いた研究が盛んに行われています⁴⁵⁶。

MCPとは、$\ell^1$ノルムよりもさらに$\ell^0$ノルムに近似でき、パラメータによって近似具合を調整できる非凸な関数です。次のように定義されます。

\begin{align}
\lambda\Phi^{\mathrm{MC}}_\gamma (\boldsymbol{q}) 
&\triangleq
\|\boldsymbol{q}\|_1 - ^\gamma\|\boldsymbol{q}\|_1 \\
^\gamma\|\boldsymbol{q}\|_1
&\triangleq
\min_{\boldsymbol{\nu} \in \mathbb{R}^m} \left(\|\boldsymbol{\nu}\|_1+\frac{1}{2\gamma}\|\boldsymbol{q}-\boldsymbol{\nu}\|_2^2 \right)
\end{align}

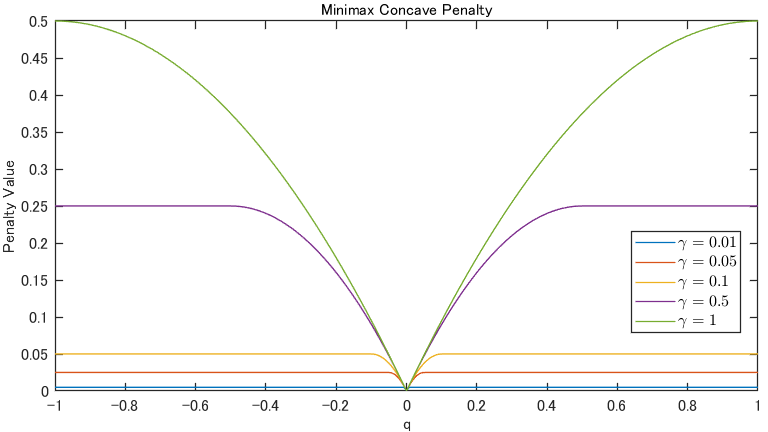
具体的に見せると、以下のような関数になります。見た目のまんま、明らかに非凸ですね。

もっと簡単に言うと。$\ell^1$ノルムは「ほら、値をゼロにせんかて」という圧力が強すぎるため、本来つながっているエッジまで無理やり細くしようとしちゃいます。一方でMCPは「小さいノイズは消すけど、明らかに繋がってそうな部分はしゃーなしやからそのまましとこ」という、調整すればいいとこ取りができる関数です。（あ、つまりパラチュン...）

主結果

導出した主問題

まず、トポロジーを推定するための最適化問題ですね。今回は確率ノイズを含むため、定常共分散行列を使って精度行列を求めます。合意ネットワークおよび白色ノイズの性質を利用することで、定常共分散行列$P_\infty \in \mathbb{R}^{n \times n}$は解析的に求まりました。

P_\infty
\triangleq
\frac{\sigma^2}{2}
\left(\left(
E\ \mathrm{diag}(\boldsymbol{q})E^{\top}+\frac{1}{n}\boldsymbol{1}_n\boldsymbol{1}_n^{\top}
\right)^{-1}
- \frac{1}{n}\boldsymbol{1}_n\boldsymbol{1}_n^{\top}
\right)

しかし、$P_\infty$は導出の過程で特異行列であることがわかり、通常逆行列をとることができません。え、このままやったら精度行列に帰着できんやんけ。そこで、微小なパラメータ$\varepsilon>0$を乗じた定数行列を加え、特異性を回避します。

P_\varepsilon 
\triangleq
P_\infty + \frac{\sigma^2 \varepsilon}{n}\boldsymbol{1}_n\boldsymbol{1}_n^{\top}

この結果をMLEに適応し、再定式化を行った結果がこちらになります。このとき、上記で加算した$\varepsilon$は定数項としてまとめられ、結果として最適化問題に影響を与えない形になりました。また、精度行列が$\boldsymbol{q}$に依存した関数であったため、決定関数は$\boldsymbol{q}$となります。

\begin{align*}
\underset{\boldsymbol{q} \in \mathbb{R}_+^m}{\mathrm{minimize}} &\quad -\log \det (E\ \mathrm{diag}(\boldsymbol{q})E^{\top}+\frac{1}{n}\boldsymbol{1}_n\boldsymbol{1}_n^{\top}) + \frac{2}{\sigma^2}\mathrm{Tr}(SE\ \mathrm{diag}(\boldsymbol{q})E^{\top}) + \lambda\Phi^{\mathrm{MC}}_\gamma (\boldsymbol{q})
\end{align*}

\begin{align*}
\mathrm{subject \ to} &\quad E\ \mathrm{diag}(\boldsymbol{q})E^{\top}+\frac{1}{n}\boldsymbol{1}_n\boldsymbol{1}_n^{\top} \succ0
\end{align*}

さてここで、凸関数$g(\boldsymbol{q}), h(\boldsymbol{q})$を以下のように定義します。

\begin{aligned}
g(\boldsymbol{q})
&\triangleq
-\log \det (E\ \mathrm{diag}(\boldsymbol{q})E^{\top}+\frac{1}{n}\boldsymbol{1}_n\boldsymbol{1}_n^{\top}) + \mathrm{Tr}(SE\ \mathrm{diag}(\boldsymbol{q})E^{\top}) + \lambda\|\boldsymbol{q}\|_1\\
h(\boldsymbol{q})
&\triangleq
\lambda^\gamma\|\boldsymbol{q}\|_1
\end{aligned}

するとどうでしょう、元の問題は次のようにみることができます。

\underset{\boldsymbol{q} \in \mathbb{R}_+^m}{\mathrm{minimize}}
\quad
g(\boldsymbol{q}) - h(\boldsymbol{q})

\begin{align*}
\mathrm{subject \ to} &\quad E\ \mathrm{diag}(\boldsymbol{q})E^{\top}+\frac{1}{n}\boldsymbol{1}_n\boldsymbol{1}_n^{\top} \succ0
\end{align*}

おやおやおや。凸関数の差をとる最適化問題、すなわちDC最適化問題 (difference of Convex functions optimization problem) と呼ばれる非凸最適化問題になるのです。
まぁ、そもそもMCPは$\ell^1$に凹な補正項を足した形になっているので、全体として凸−凸（つまりDC）構造になるのは自然ですよね。
なので、$g$は「元のGraphical Lasso的な凸問題」、$h$は「MCP由来の凸な補正項」と見ることができるわけですな。

さて、本来であれは非凸最適化問題は嬉しくないクラスです。しかし、嬉しいことにですね。このクラスの最適化問題は解くためのアルゴリズムが良く研究されております。今回はもっともよく知られているアルゴリズム、 DC Algorithm (DCA)⁷ を使って求解を行いました。

以下に、本論文におけるDCAを示します。わかる人にはわかりますが、すんごい基本的なDCAです。

なお、アルゴリズム中で登場する$\nabla h$はしきい値関数として解析的に求まり、微分計算することなくアルゴリズムを回すことができます。

シミュレーション結果

さてさて、では砲塔に推定結果良くなるのか見てみましょう。この論文で書かれている100個のノードを持つネットワークで推定するとまぁとんでもなく時間かかる（早くて3時間ぐらい）ので、簡単なネットワークでやりましょう。

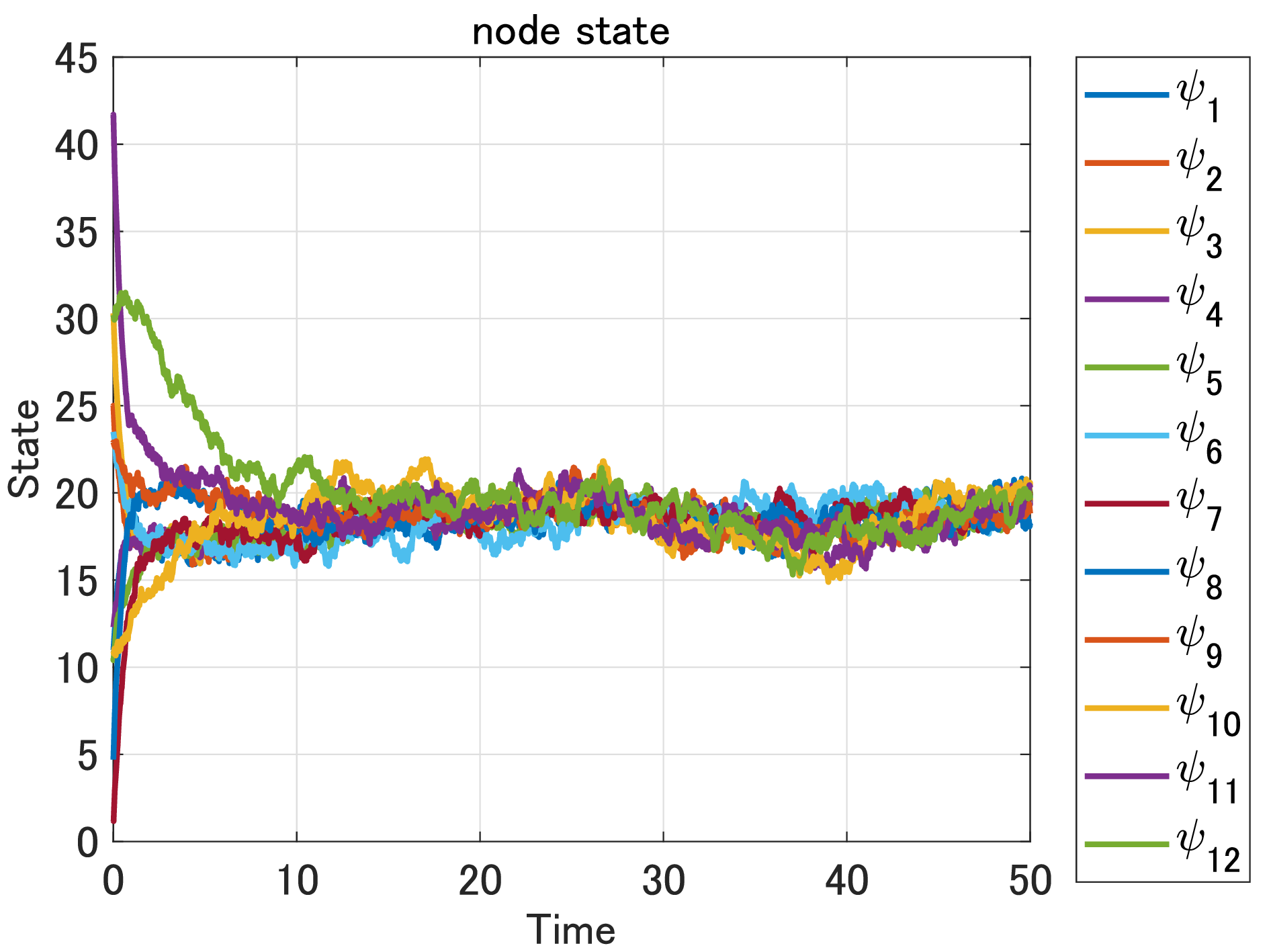
次に示す12個のノードを有する合意ネットワークを対象に推定します。

このネットワークは次のような状態遷移で合意を達成します。ノイズマシマシですね。ノード少なめノイズマシマシ標本データマシマシで（二郎風）。

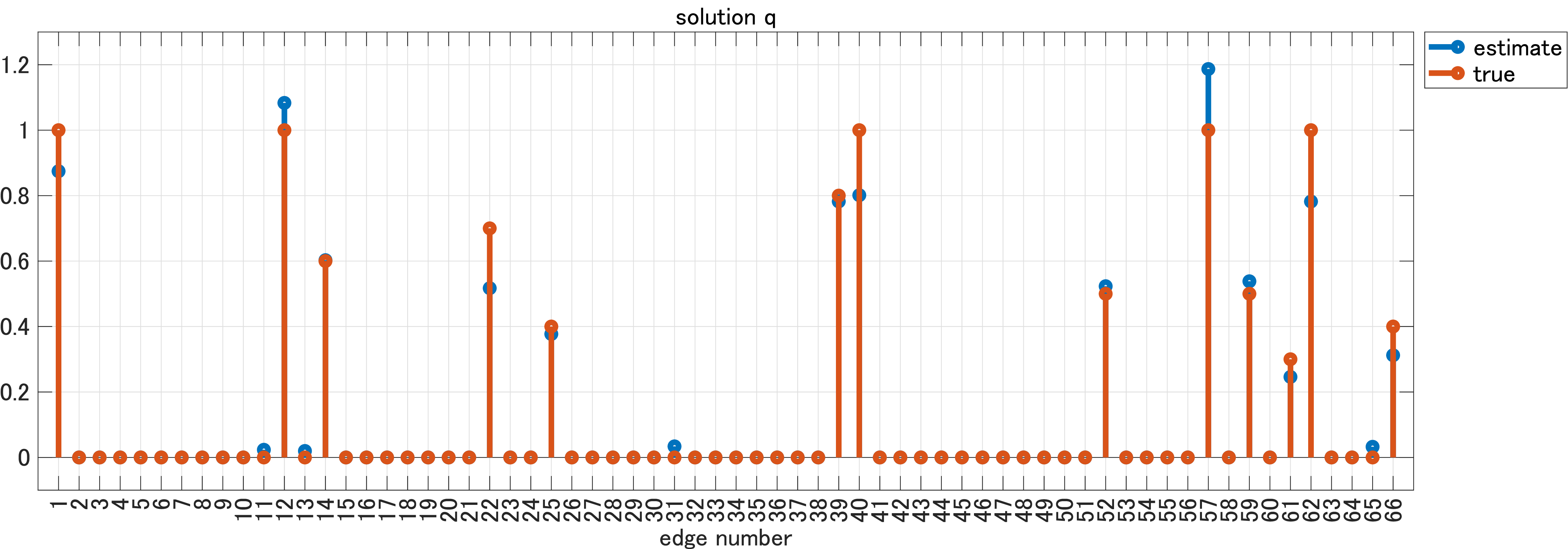
結果は以下のようになりました。比較として、従来手法である$\ell^1$ノルムを使用した推定結果も載せておきます。

まずは、MCPの結果から。

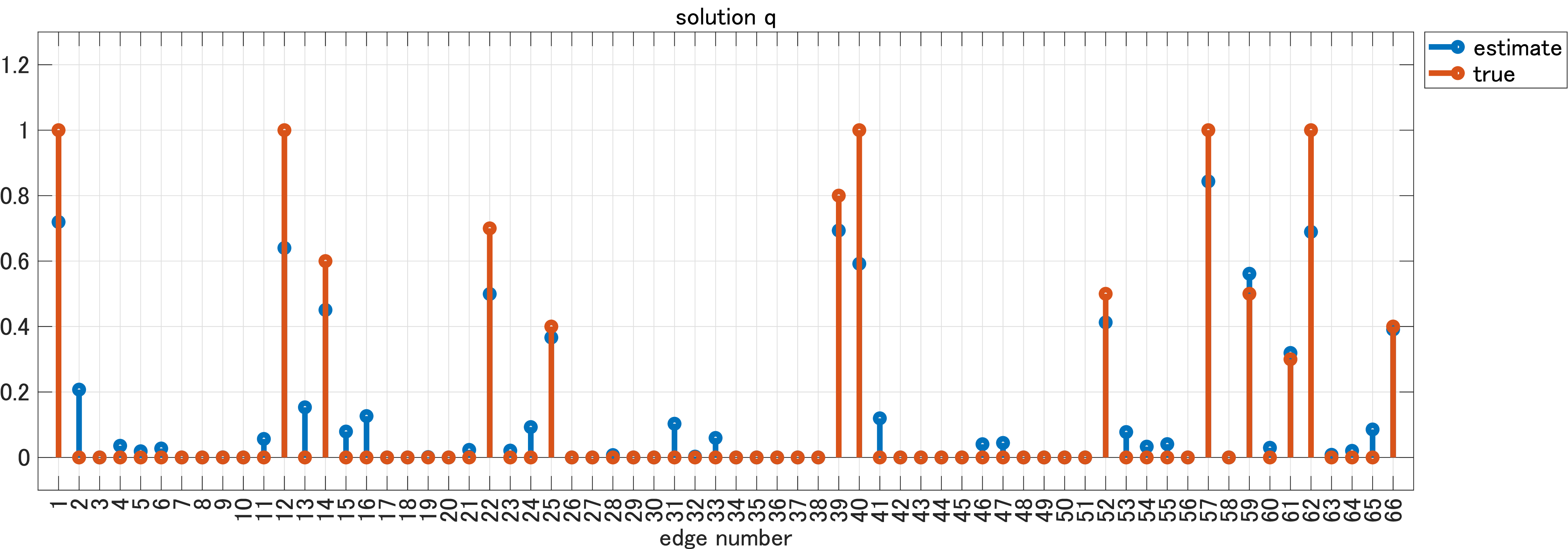
次に、$\ell^1$ノルムの結果。

小規模でもある程度の有意差が見れましたね。ちなみに、論文中の大規模ネットワークだと、$\ell^1$が推定二乗誤差1.1001に対してMCPは推定二乗誤差0.0309でした。

あと、論文内では群ドローンの高度に対して合意制御を行い、そのデータをもとに推定を行うという実証実験も行っていますが、ここでは割愛させていただきます。興味のある人はぜひ本文を。

おわりに

いかがでしたか？オチが全く無いです。他にも、SCADやL1/L2といった非線形なスパース正則化項があるので、気になる人はぜひ調べてみてください。
また、純粋に繋がっているかどうかだけの判定（0 or 1の二値推定）も先行研究としてあるので、興味があってIEEE Control Systems Society (CSS)に加入されている人は読んでみるといいかもしれないです⁸。

それでは、また今度。

1. O. Banerjee, L. El Ghaoui, and A. d’Aspremont, "Model selection through sparse maximum likelihood estimation for multivariate Gaussian or binary data," J. Mach. Learn. Res., vol. 9, pp. 485–516, 2008. ↩

2. J. Ying et.al., "Nonconvex sparse graph learning under Laplacian constrained graphical model," in Proc. Adv. Neural Inf. Process. Syst., vol. 33, 2020, pp. 7101–7113. ↩

3. J. Woodworth and R. Chartrand, "Compressed sensing recovery via nonconvex shrinkage penalties," Inverse Probl., vol. 32, no. 7, 2016, Art. no. 75004. ↩

4. C.-H. Zhang, "Nearly unbiased variable selection under minimax concave penalty," Ann. Stat., vol. 38, no. 2, pp. 894–942, 2010. ↩

5. I. Selesnick, "Sparse regularization via convex analysis," IEEE Trans. Signal Process., vol. 65, no. 17, pp. 4481–4494, Sep. 2017. ↩

6. S. Wang et.al., "Vector minimax concave penalty for sparse representation," Digit. Signal Process., vol. 83, pp. 165–179, Dec. 2018. ↩

7. P. D. Tao and L. T. H. An, "Convex analysis approach to DC programming: Theory, algorithms and applications," Acta Mathematica Vietnamica, vol. 22, no. 1, pp. 289–355, 1997. ↩

8. F. Matsuzaki, R. Yotsumoto and T. Ikeda, "Sparse structure learning for consensus network systems via sum-of-absolute-values regularization," in Proc. 62nd Annu. Conf. Soc. Instrum. Control Eng., Tsu, Japan, 2023, pp. 478-483, 2023. ↩