初めての合意制御（連続時間系）

はじめに

皆様こんにちは，ざきまつです．
永遠の制御・数学初心者をさせていただいています．

後輩「合意ネットワークについて卒論で取り組んでいるんですよ」
僕「楽しいじゃん（合意ネットワーク大好きﾏﾝ）」
後輩「でも，新しい数学が入ってきてよくわかんなくて」
僕「ﾅｰｰｰｰﾆｰｰｰｰ!?」

というわけで，この記事では合意制御について基礎的な内容を扱っていこうと思います．
合意ネットワークおよび合意制御は，群制御において基礎的な問題としてよく扱われます．
今後，協調制御をやっていく中で確実に触るものなので，後輩や勉強されている方々に向けて書いておこうというサムシングになっております．

かなり数学的な内容になっていますが，初心者でもわかりやすいようにﾓｸﾞﾓｸﾞ噛み砕いていきます．
質問があれば，気軽にコメントやTwitterX (@santana_hammer)のDMにてお知らせください．
それでは，やっていきましょうか．

最近，群ロボットやドローンネットワークの研究が結構盛んに行われている印象です．
これらは「マルチエージェントシステム(Multi-Agent System:MAS)」と呼ばれるシステムに属しており，わりかし最近ホットな研究トピックな気がしなくもなくも（以下略）

[10/28 追記]
固有値のインデックスを間違えていたので修正しました．

合意制御 #とは

マルチエージェントシステムの制御手法の一つであり，簡単に言うと「みんなが同じ状態値に収束するような制御」です．

詳細については後述しますが，ゆるふわな説明をすると．
こちらから明示的に目標値を設定することなく，「ネットワークにいるみんなで頑張って考えてね☆」という制御器を全エージェントに対して搭載する制御手法になっています．

例えば，小学校や中学校で「基準！！体操の隊形に開け！！」みたいなやつありましたよね．他にも，「前に倣え！！」とかありましたよね．
前後左右を確認し，みんなと合わせつつ綺麗な隊形を作る...まさにみんなで「あいつがこうだから，これくらいかな」と合意を形成しながら並んでいるわけですね．
これが合意制御，あるいは合意ネットワークです．

実際に制御器を組み込む際は，座標を一致させる他にも速度，角度などといった状態値に対して組み込まれることが多いです．

Mathematic Preliminary

ここでは，合意制御について知る時に必要となる数学知識について記述します．
なお，線型代数学の基礎知識（固有値・固有ベクトルの話まで）がわかることが前提です．

ですが，僕は「お気軽のプロ（らしい）」なので，わからない人もビビらずに見ていただけると．

グラフ理論

ネットワークの構造を表すのにベストgoooooooooodな数学分野です．
筆者の英語能力の低さが垣間見えますね．

グラフ理論自体は奥深い分野ではありますが，ここでは合意制御で使用する必要最低限の知識だけ記述します．

グラフとは

グラフを構成する$n$個の頂点集合を$\nu$とします．この集合には$n$個の頂点が含まれるので$\nu = ${$1, 2, \dots, n$}と表現します．
その中で構成されるつながった組み合わせを$\varepsilon$とし，$\varepsilon$は頂点同士の組み合わせになるため$\varepsilon \subseteq \nu \times \nu$と表現します．

以下，頂点を 「エージェント」もしくは「ノード」 ，辺を 「エッジ」 と表現します．

ここで，「記号わかんねぇぜ！！ﾊﾊﾊ☆」となった人は是非ググってください．
数学の集合関係で出てきた記憶です．

この記事に関わらず，制御理論で登場する数学記号の意味がわからないという方は，「あれっ，大学で数学がわからなくなった！」という本が大変おすすめです．
制御工学でよく出てくる集合記号やその意味，どうしてそうするかの意図など大変丁寧に書かれています．

あれっ，大学で数学がわからなくなった！ - コロナ社

隣接行列 (Adjacency Matrix)

エージェント（またはノード）間の接続を示す行列であり，$A \in \mathbb{R}^{n \times n}$と表現されます．
行と列はシステム内のエージェントを表し、各要素の値はそのエージェント間の接続を表しています．
各要素は以下のように定義されます．

\begin{align}
[A]_{ij} 
= a_{ij} =: 
\begin{cases}
1 & \text{if} \ (i, j) \in \mathcal{E}\\
0 & \text{otherwise}
\end{cases}
\end{align}

僕みたいに数学が苦手な人 いまいちピンとこない人向けにゆるふわ説明すると．
$i$さんは$j$さんと繋がりを持っているかどうか，繋がっていたら1，繋がっていなかったら0が入る行列です．

ツイ廃（X廃？）の人向けの説明をすると，フォローしていたら1，フォローしてなかったら0ってことですね．
フォロバ率100%の人だったら隣接行列は対称行列，そうでなければ非対称行列になります．

次数行列 (Degree Matrix)

各エージェント（ノード）がどれだけ多くのエージェントと接続しているかを示す対角行列（対角線上にしか要素が並んでいない行列）であり，$D \in \mathbb{R}^{n \times n}$と表現されます．
対角要素はそのノードの「次数」（接続の数，何人と繋がっているか）を示し，非対角要素は全て0になります．
各対角要素は以下のように定義されます．

\begin{align}
[D]_{ii} := \sum_{j=1}^{n} a_{ij}
\end{align}

グラフラプラシアン (Graph Laplacian)

グラフの構造を表す行列で，次数行列と隣接行列の差によって定義され，$L \in \mathbb{R}^{n \times n}$と表現されます．

\begin{align}
L := D - A
\end{align}

エージェント間の相対的な位置関係や，全体としての接続性の特性を分析するのに使用される行列です．
「こいつは今，何人と繋がっていて誰と誰と誰と繋がっている」という情報を格納していると思ってください．

この行列はいくつか特性を持っています．

1. $L$は固有値0を最低でも一つ持ち，それに対応する固有ベクトルは$\textbf{1}_{n}$（要素が全て1の$n$次元ベクトル）である．
2. 0以外の固有値は，開右半平面に存在．
3. 特に無向グラフの場合，固有値はすべて非負の実数になる．

これ以外にもいろいろあるんですが，とりあえずこれだけにしておきます．

なお，以下ではネットワークの通信方向に制限が全くない「無向グラフ」を前提に進めていきます．
（繋がっていたら，お互いに情報交換できる状態を仮定します．）

連続時間系における制御器

それでは，本題である連続時間系における合意制御について触れていきます．
連続時間系における制御器は，以下のように記述されます．

\dot{x}_{i}(t) = -\sum_{j \in \mathcal{N}_{i}} \left( x_{i}(t) - x_{j}(t) \right)

$\mathcal{N}_{i} \subseteq \nu$はエージェント$i$と繋がっている他のエージェント（隣人）の集合です．

上述した制御器はエージェント1つ1つに関するものですが，全エージェントの制御器をまとめて記述することが可能です．
グラフ理論のセクションで説明した隣接行列の要素表現を用いて，以下のように書き換えてみましょう．

\begin{align}
\dot{x}_{i}(t) &= -\sum_{j \in \mathcal{N}_{i}} \left( x_{i}(t) - x_{j}(t) \right)\\
&= -\sum_{j=1}^{n} a_{ij}\left( x_{i}(t) - x_{j}(t) \right)
\end{align}

総和記号の部分が，元々は隣人の集まりだったのが全探索に変わりましたね．
これを全てのノードについて記述し，一つの状態ベクトルにまとめると，以下のように変形できます．

\begin{align}
\dot{x}(t)
&=
\begin{bmatrix}
\dot{x}_{1}(t)\\
\dot{x}_{2}(t)\\
\vdots\\
\dot{x}_{n}(t)
\end{bmatrix}\\
&=
\begin{bmatrix}
-\sum_{j=1}^{n} a_{ij}\left( x_{i}(t) - x_{j}(t) \right)\\
-\sum_{j=1}^{n} a_{ij}\left( x_{i}(t) - x_{j}(t) \right)\\
\vdots\\
-\sum_{j=1}^{n} a_{ij}\left( x_{i}(t) - x_{j}(t) \right)
\end{bmatrix}\\
&=
\begin{bmatrix}
-d_{i}^{in} & a_{12} & \ldots & a_{1n}\\
a_{21} & -d_{2}^{in} & \ldots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{n1}& a_{n2} & \ldots & -d_{n}^{in}\\
\end{bmatrix}
\begin{bmatrix}
x_{1}(t)\\
x_{2}(t)\\
\vdots\\
x_{n}(t)
\end{bmatrix}
\end{align}

カッコがすんごいバグっちゃってますね．右辺に記述されている$n \times n$の行列は，グラフラプラシアン$L$の符号を反転した形になっています．

上記の内容より，以下の式が成り立ちます．

\dot{x}(t) = -Lx(t)

とてもシンプルに記述できました．

ちなみに，ネットワークが全体で合意を形成するにはネットワークが連結である必要があります．
これは，ネットワークが複数に分裂したり，ボッチなエージェントがいると合意が形成できないっていう意味になります．チームって難しいね...

合意達成の解析

ここでは，上述した制御器が本当に合意を達成できるのかどうか，数学的に解析します．

\dot{x}(t) = -Lx(t)

この微分方程式の解は，以下のように得られます．

x(t) = e^{-Lt}x_{0}

ここで，$L$は重複も含めて$n$個の実固有値を持っていることが知られています．$n$個の実固有値を$\lambda_{1}, \lambda_{2}, \dots, \lambda_{n} \in \mathbb{R}$と表現しましょう．
また，各実固有値に対応する固有ベクトルは 大きさが1，かつ互いに直行するように選ぶことが可能です．固有ベクトルをここでは$v_{1}, v_{2}, \dots, v_{n}$としましょう．

そういえば，グラフラプラシアンの性質に以下のものがありましたね．

$L$は固有値0を最低でも一つ持ち，それに対応する固有ベクトルは$\textbf{1}_{n}$（要素が全て1の$n$次元ベクトル）である．

この性質を使うことで，次のことが言えるようになります．

\begin{align}
\lambda_{1}=0, \ v_{1}=\frac{1}{\sqrt{n}}
\end{align}

これらをうまく使って，合意がちゃんと達成できるかを確認してみましょう．
以下，議論を簡単にするために$U$を次のようなものとして定義します．

\begin{align}
U := \begin{bmatrix}v_{1}&v_{2}&\dots&v_{n}\end{bmatrix}
\end{align}

さて，微分方程式の解をゴニョゴニョしましょう．
$x_{0}$は初期値であるため，定数となります．となると，気になるのは時間変数となっている$e^{-Lt}$がどう動くかですね．
固有値と固有ベクトルを使って，うまく分解してやると以下のようになります．

\begin{align}
e^{-Lt}
&= e^{-U \text{diag}(\lambda_{1}, \lambda_{2}, \dots, \lambda_{n})U^{\top}} \\
&= Ue^{-\text{diag}(\lambda_{1}, \lambda_{2}, \dots, \lambda_{n})}U^{\top}\\
&= 
\begin{bmatrix}
    v_{1} & v_{2} & \dots & v_{n}
\end{bmatrix}
\begin{bmatrix}
    e^{-\lambda_{1}t} & 0 & \dots & 0 \\
    0 & e^{-\lambda_{2}t} & \dots & \vdots \\
    \vdots & \ddots & \ddots & 0\\
    0 & \dots & 0 & e^{-\lambda_{n}t}
\end{bmatrix}
\begin{bmatrix}
    v_{1}^{\top} \\ v_{2}^{\top} \\ \vdots \\ v_{n}^{\top}
\end{bmatrix}\\
&= \sum_{i=1}^{n} e^{-\lambda_{i}t}v_{i}v_{i}^{\top}
\end{align}

お，なんかいい感じな形になりました．
ここで，$v_{1}$についてだけ取り出して再度書き直してみましょう．

\begin{align}
x(t) = \frac{1}{n}\textbf{1}_{n}\textbf{1}_{n}^{\top}x_{0} + \sum_{i=2}^{n} e^{-\lambda_{i}t}v_{i}v_{i}^{\top}x_{0}
\end{align}

定数項の爆誕です，嬉しいですね．え，嬉しさがわからない？

最後に極限を取ってみると，以下のような結果を得ることができます．

\begin{align}
\lim_{t \to \infty} x(t) 
= \frac{1}{n}\textbf{1}_{n}\textbf{1}_{n}^{\top}x_{0}
= \frac{1}{n}(\textbf{1}_{n}^{\top}x_{0})\textbf{1}_{n}
\end{align}

時間依存項がなくなりました，嬉しいですね．え，嬉しさが（以下省略
つまり十分時間が経過するとある一定の値すなわち，ある合意値に収束（合意を達成）することがわかりますね．

シミュレーション

では最後に，シミュレーションでどんな動きするのか見てみましょう．
ここでは，オイラー法利用して常微分方程式を解いています．
ソースコードはこちら！！

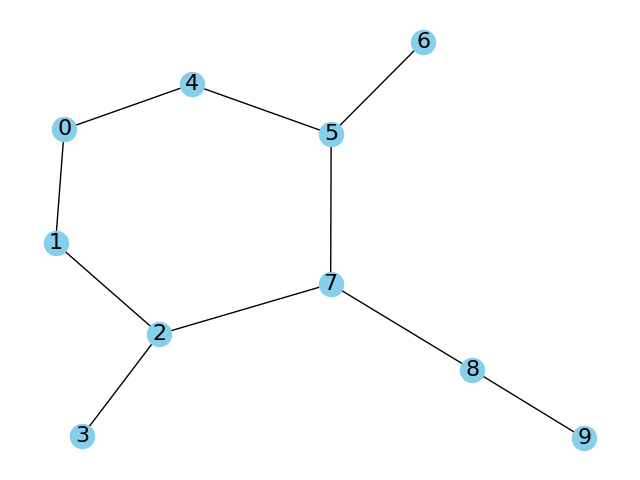
こんな感じのトポロジーを設定してみました．

結果は以下のようになっています．

綺麗に一定値に収束しています．
うん，言うことないね．以上閉廷，解散解散解散解散．

終わりに

次回は離散時間系だよ！！
お楽しみに！！

参考文献

[1] 東俊一ほか，マルチエージェントシステムの制御，コロナ社，2015．
[2] 林直樹，永原正章，マルチエージェントシステムの制御-II 代数グラフ理論，システム/制御/情報，57 (7)，pp. 283 - 292，2013．
[3] 桜間一徳，マルチエージェントシステムの制御-III 合意制御 (1)，システム/制御/情報，57 (9)，pp. 386 - 396，2013．