はじめに
これまでに色々と非凸最適化とか近接勾配法とか書いてきましたが,いちばんの基礎である凸最適化について書いていませんでした.
基礎を飛ばして応用例というかその領域について書いていくなんて,鬼教官も涙目ですね.
なので,この記事では超ざっくりに凸最適化について触れていこうと思います.
それでは,やっていきましょうか.
凸集合
まず,凸最適化の土台である凸関数の土台である凸集合について触れます.
定義
ある集合$C$を定義する.任意のベクトル$x_1, x_2 \in C$に対して
x_1, x_2 \in C, \\
\theta \in [0, 1] \Rightarrow (1-\theta) x_1 + \theta x_2 \in C
が成り立つとき,集合$C$は凸集合であるという.
何言うてるかわかりませんね,図で見てみましょう.
凸集合を図で描くと...
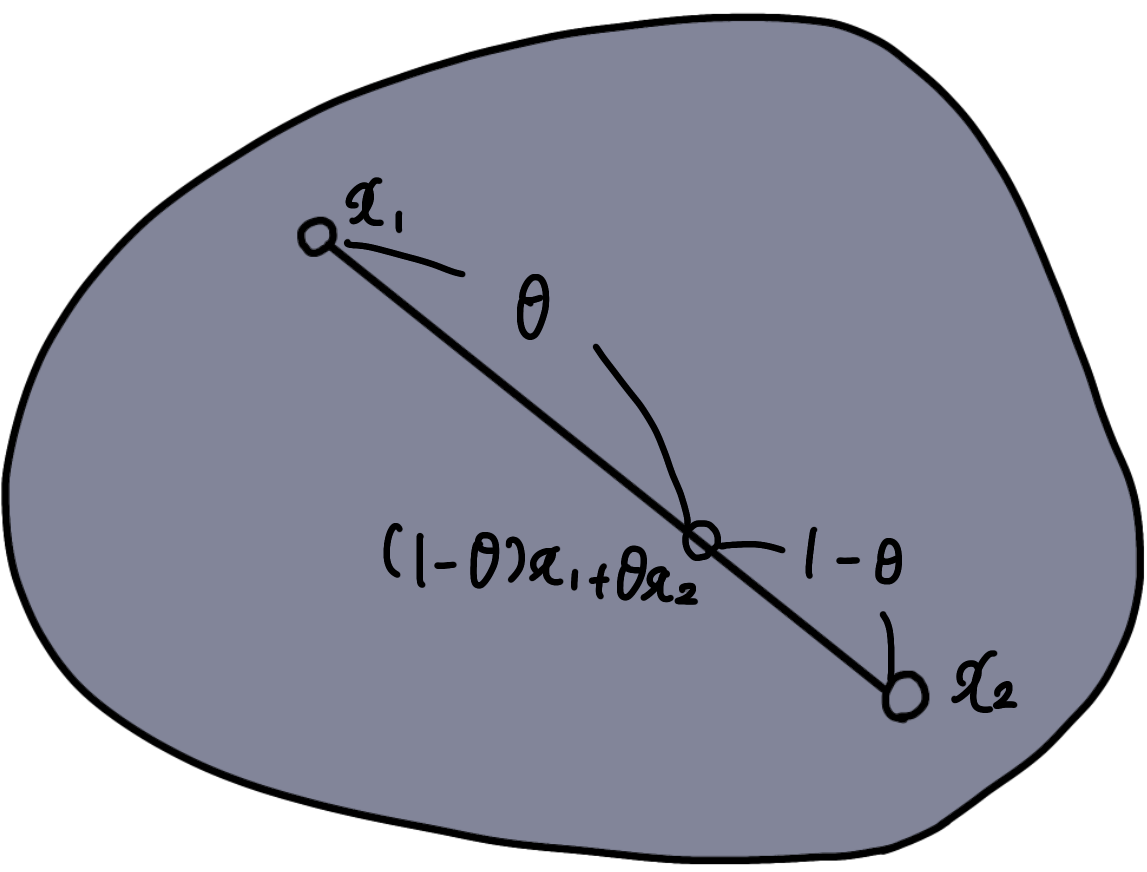
こんな感じです.グレーの部分を集合$C$としています.直感としては,任意の点$x_1, x_2 \in C$を結んだ線分の内分点が集合$C$上に存在することです.
もし,凸集合じゃなかった場合はどうなるか?
その場合は...
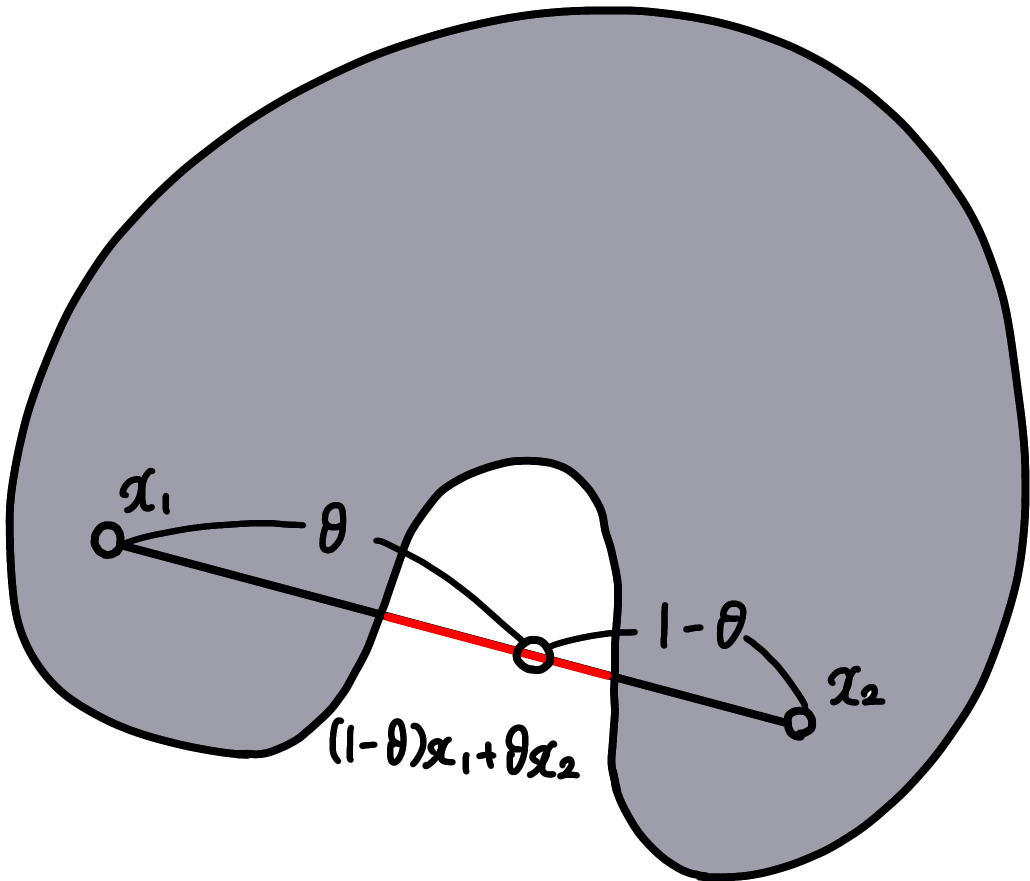
こんな感じですね.赤線部分が集合の外に出ています.内分点のどっかが集合$C$に入っていなければ,こいつは凸集合とは言えません.このような集合のことを,凹集合(非凸集合)と呼びます.
上記の内容をまとめると
- 集合内のどこでもテキトーに点を二つ取ってきて,それを線分で結んで.
- その線分の中でどこで点を取っても,必ず集合に含まれている.
ってことになります.
凸関数
次に,凸最適化を構成する大事な要素の凸関数について触れていきます.
定義
ある実数値関数を$f$とする.$f$のエピグラフが凸集合のとき,$f$は凸関数である.
さぁ,エピグラフとかいうものが出てきました.美味しそうな名前ですねって,それはエビピラフなんよ.確かに似ていますけども.
エピグラフは以下のように定義されるものです.
エピグラフ
以下の集合は,$f$のエピグラフである.
\text{epi} \ f \triangleq \{ (x, y) \in {\mathbb{R}}^n \times {\mathbb{R}} : y \geq f(x) \}
数式見てもよーわからんですね,お気持ちわかります.
これもまた図で表すとわかるかもですね.
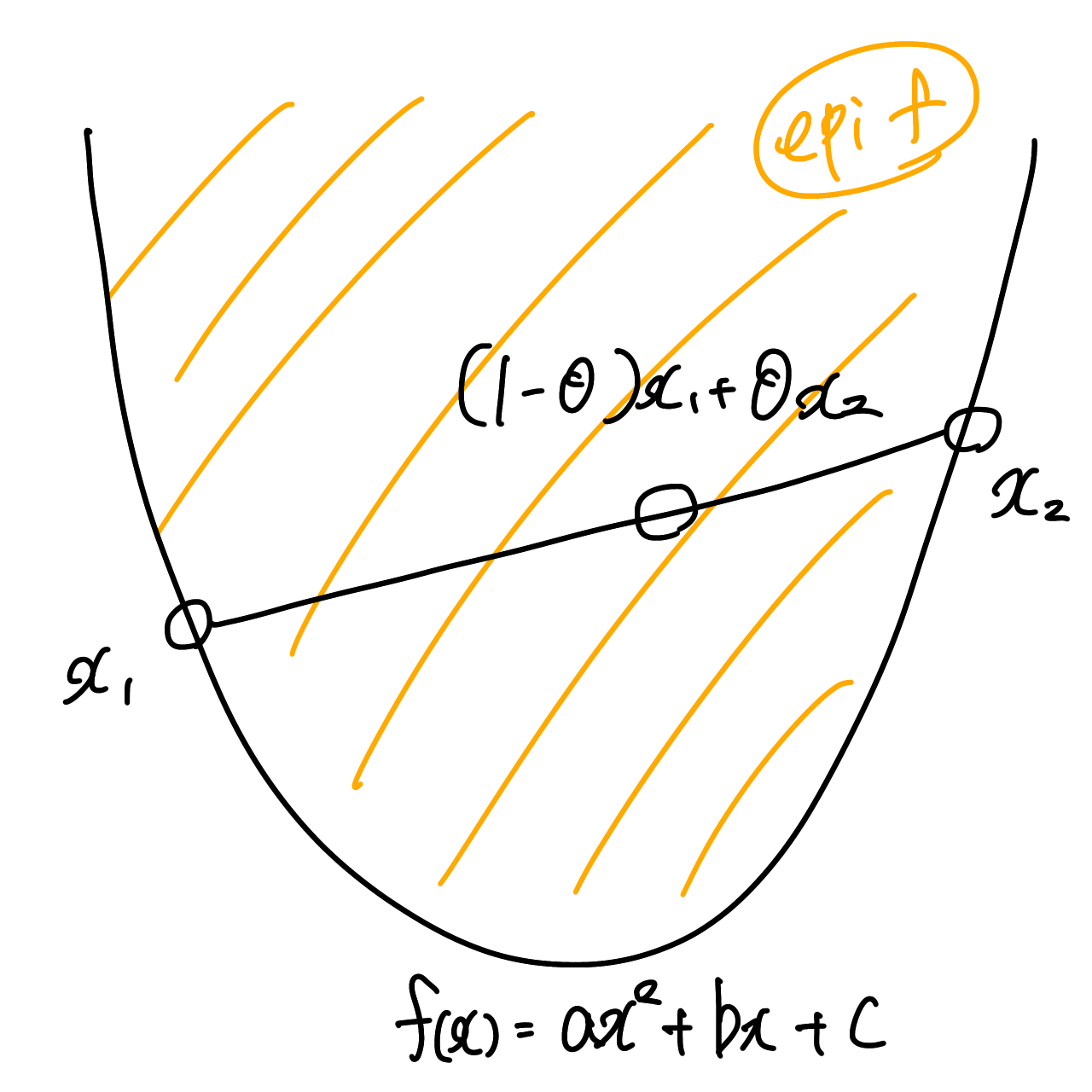
図の中の,オレンジ色の部分がエピグラフです.関数が成すグラフの上部(?)を指しています.
つまり,関数がなすグラフの上部分が凹んだりしていなければ,こいつは凸関数と言って良いんですね.
以上二つの定義より,凸関数は一般的に以下のように表されます.
(1 - \theta)f(x_1) + \theta f(x_2) \geq f \left( (1 - \theta)x_1 + \theta x_2 \right)
まとめると,凸関数の定義の簡単な解釈としては
- 関数の上側が凹んだりしていなければ,凸関数(下に凸)
という感じでしょうか.
ちなみに
「凸があるなら,凹もあるのでは??」と思われた方もいるかと思います.
あります.えぇ,ありますとも.
以下に,凹関数の定義を記述します.
定義
ある実数値関数を$g$とする.$g$の符号反転が凸関数である時,$g$は凹関数である.
なんてわかりやすいんだ...感動的ではないか.
これまでの理解の苦労はなんだったんですかね.
ちなみに,式で表すとこんな感じです.
(1 - \theta)f(x_1) + \theta f(x_2) \leq f \left( (1 - \theta)x_1 + \theta x_2 \right)
凸関数の時と不等号が反転していますね.これが凹関数です.
凹関数の代表例としては
- 対数関数 $g_1(x) = \log x$
- 正弦関数 $g_2(x) = \sin x$ ($0 \leq x \leq \pi$)
- 二次関数 $g_3(x) = -x^2$
- 平方関数 $g_4(x) = \sqrt{x}$
などが挙げられます.非常にイメージしやすいのではないでしょうか.
凸最適化問題
さてさて,ここまでさっくり触れてきた凸集合・凸関数の知識を使って,凸最適化問題について知っていきましょう.
関数$f: \mathbb{R}^n \to \mathbb{R} \cup { \infty }$がプロパーな凸関数,かつ集合$C \subset \mathbb{R}^n$が閉凸集合であるとき,$x \subset C$の中で$f(x)$を最小にする$x$を求める問題.
なんだこれは,全くもってわからんぞ(初心者の声)
新しい用語が出てきました,「プロパー」.なんでしょうねこれ.
制御屋さんなら聞いたことあるかもしれません,てか現代制御やったことある人は知っとかなきゃいけない知識です.
以下,プロパーについて説明します.
プロパー
$f(x)<\infty$となるような$x$が一つでも存在する($\text{dom} \ f \neq \varnothing$)とき,関数$f$はプロパーであるという.
「$\text{dom} \ f$」ってなんだ,ドムドムバーガーで売ってそうなフロートのことか.
違います,この「$\text{dom} \ f$」というのは実効定義域というものです.
実効定義域
関数$f$の定義域のうち,$f(x)$が実数値を取るような$x$の集合を,$f$の実効定義域と呼ぶ.
\text{dom} \ f \triangleq \{ x \in \mathbb{R} : f(x) < \infty \}
つまり,何かしら有限な値を取るような$x$の集合のことを指しています.
- 関数$f$が無限大に発散さよならバイバイせず,かつ凸関数である
- ある値$x$が閉凸集合に含まれる
この時に,$f(x)$を最小化する$x$を求める問題を凸最適化問題と言います.
凸最適化問題の嬉しいポイント
さてさて,凸最適化について駆け抜けてきました.
最後に,凸最適化問題の嬉しいポイントについて紹介します.
大域的な最適値を得ることができる
一般に,勾配情報を利用した最適化手法では,局所的な最適値に収束することが多いです.
凸最適化では,評価関数の凸性が担保されているため,大域的な最適値を得ることができます.
最適化計算の速度が速い
凸最適化特有の最適化手法を用いることで,汎用の最適化手法よりも計算時間を短縮することが可能です.
何か,最近では更に高速化を目指した手法があるとかなんとか.
おわりに
いかがでしたか?
凸最適化について,少しでもイメージできたり「なるほどな」となって頂けたら嬉しいです.泣いて喜びます.
もっと知りたい方がいましたら,以下の記事をお勧めいたします.
凸最適化の概要と主双対内点法のアルゴリズムの解説 - taka_horibe
数理計画 ~目次~ - momo10(ひでき)
それでは,また今度.
参考文献
- 永原正章, "スパースモデリングー基礎から動的システムの応用ー", コロナ社, 2017.