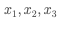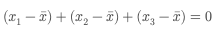共分散とは
2つのデータセットの間で、一方のデータが変動したときに、もう一方のデータがどの程度連動して変動するかを示す指標です。
🎯 結論から言うと…
とするのは、母集団の共分散（真の値）を推定するために、標本から計算した共分散の“偏り”を補正するためです。
🧩 1. 「母集団」と「標本」の違い
| 用語 | 内容 |
|---|---|
| 母集団（Population） | 本来知りたい全体のデータ（例：全国の全ての車の燃費） |
| 標本（Sample） | 実際に観測できる一部のデータ（例：100台分だけ測った燃費） |
私たちは普通、母集団全体のデータはわからないので、
一部の標本データから「母集団の共分散」や「母分散」を推定します。
🧮 2. nではなく(n−1)にする理由（自由度）
平均を使うとき、実は「データの自由度」が 1 減ります。
例：
データが3つあるとき
平均 
を使うと、
次の関係が必ず成り立ちます：
つまり、3つのうち2つの偏差が決まれば、残り1つは自動的に決まってしまいます。
→ 「自由に変えられるデータが1つ減る」ということ。
→ この残りの“自由な数”を 自由度（degrees of freedom） と呼びます。
したがって：
• データが n 個あるなら
→ 自由度は n − 1
🧠 3. もし n で割るとどうなる？
もし単純に n で割ると、
偏差 (x_i - \bar{x}) を計算に使っているために、
実際よりも**分散・共分散が小さめ（過小評価）**になります。
これは「平均を標本から推定している」せいで、
本当のばらつきよりも“少し小さく見積もる”ことになるからです。
✅ 4. だから補正する
その「小さく見積もる分」を補正するために、
割る数を n ではなく n − 1 にして平均を少し大きくします。