はじめに
最近,VAE(Variational Autoencoder)やGAN(Generative Adversarial Networks)等のモデルを学んでいますが,これら生成モデルの話で必ず登場するのが Kullback-Leibler divergence という用語です.機械学習の用語において,「クロス・エントロピー」や「ドロップアウト」でしたら,英単語と物理,数学の知識でなんとなく想像がつきますが,「カルバック・ライブラー」という言葉を初めてみたとき,「???」となる方も多いのではないでしょうか? 特にボルツマンマシンから生成モデルに入ると,計算手法のCD(コントラスティブダイバージェンス)も新しい用語として登場して来るので,「生成モデルって...難しい」となりがちです.本記事では,図を見ながら "Kullback-Leibler" を理解していきたいと思います.
まず,日本語Wikipediaから引用させていただきます.
カルバック・ライブラー情報量(英語: Kullback–Leibler divergence、カルバック・ライブラー・ダイバージェンス)とは、確率論と情報理論における2つの確率分布の差異を計る尺度である。情報ダイバージェンス(Information divergence)、情報利得(Information gain)、相対エントロピー(Relative entropy)とも呼ばれる。
これだけで大体理解される方も多いのではと思います.カルバックライブラー情報量 = エントロピー となればコンセプトはさほど難しくはありません.また,こちらは雑学的な知識になりますが,
The Kullback–Leibler divergence was originally introduced by Solomon Kullback and Richard Leibler in 1951 as the directed divergence between two distributions; Kullback himself preferred the name discrimination information. (from en.wikipedia)
とのことで,これは,KullbackさんとLeiblerさんが考案したもののようです.
(統計モデリングで使われる,"AIC" も 赤池さん's Information Criterionですので,命名の経緯は似ていますね.)
定義としては,以下の式になります.
D_{KL} (P || Q) = \sum_i {P(i)\ log \frac{P(i)}{Q(i)}}
上式において,P(i),Q(i) は,2つの確率分布になります.式としては,それほど複雑のものではなく,また,"log" と分数式が出てくるところは,分類問題のクロス・エントロピーにかなり似ています.一方,「距離」の公理に照らし合わせてみると,「非負性」は満たしますが,「対称性」 $$ D_{KL}(P,Q)\ =\ D_{KL}(Q,P)$$ は満たしませんので,「距離」のコンセプトからは外れるようです.
簡単な分布でKL divergenceを求めてみる
簡単な分布,まず初めに平均の異なる2つの正規分布で Kullback-Leibler divergence(以下,DKL)を求めてみたいと思います.
Pythonで確率分布を計算するのに,scipy.stats の関数を用いました.また DKL の計算には scipy.stats.entropy() が使えることが分かりました.(参考,Scipyドキュメント:https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.entropy.html )
前記のDKL定義式においてlog(自然対数)が入るので,log引数が0となるケースは注意が必要ですが,以下の例では特に問題はありませんでした.)
作成したコードが以下になります.
import numpy as np
from scipy.stats import norm, skewnorm, entropy
import matplotlib.pyplot as plt
ndiv = 100
px = np.linspace(norm.ppf(0.001), (norm.ppf(0.999) * 1.1), ndiv)
# Shifted normal distributions
fig, axes = plt.subplots(3, 3, figsize=(8, 8), sharey=True)
loc_opts = np.array([i * 0.1 for i in range(9)])
loc_opts = loc_opts.reshape([3, 3])
pdf_std = norm.pdf(px, loc=0., scale=1.) # reference distribution
py_zero = np.zeros_like(px) # y=0.0 line
for i in range(3):
for j in range(3):
norm_ij = norm(loc=loc_opts[i, j], scale=1.)
pdf_ij = norm_ij.pdf(px)
ax_ij = axes[i, j]
ax_ij.fill_between(px, pdf_std, py_zero, color='b', alpha=0.3)
ax_ij.fill_between(px, pdf_ij, py_zero, color='r', alpha=0.3)
ax_ij.set_xticklabels([])
dkl_ij = entropy(pdf_std, pdf_ij)
title_str = 'DKL={:>.3f}'.format(dkl_ij)
ax_ij.set_title(title_str)
正規分布の平均値(中央値)を,[0.0, 0.1, ..., 0.8] と設定してDKLを計算しました.
Fig.1 Normal Distributions (shifted)
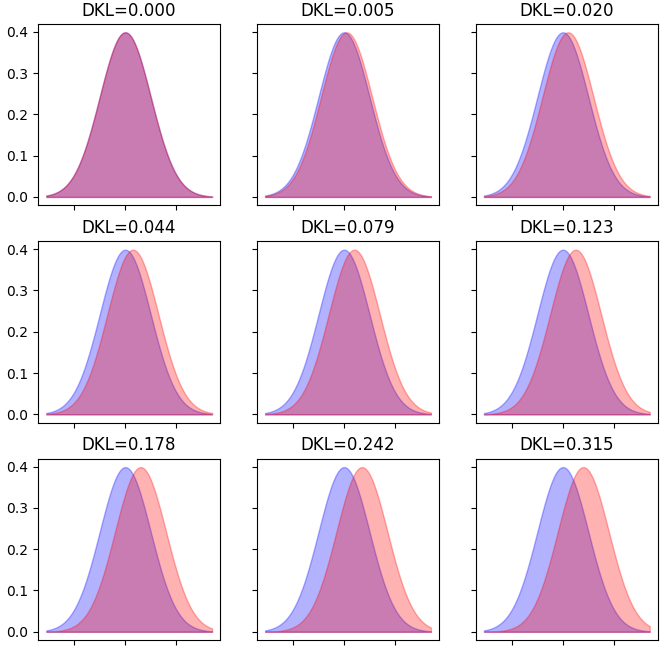
基準となる「青」の分布とシフトした「赤」の分布の間の DKL を算出し,タイトルに示しています.シフト量=0 で DKL=0 となることが確認できました.また,2つの分布が重ならない部分(紫になっていない,青と赤のエリア)面積と DKL 値が正の相関を持っているのがよく分かるかと思います.2つの各分布は,プログラム内では離散値を持っているので,面積を求めてみましたが,線形の関係にはなりませんでした.
s = 0.0000, DKL = 0.0000
s = 1.2105, DKL = 0.0049
s = 2.4190, DKL = 0.0197
s = 3.6210, DKL = 0.0444
s = 4.8121, DKL = 0.0790
s = 5.9891, DKL = 0.1234
s = 7.1529, DKL = 0.1776
s = 8.2951, DKL = 0.2416
s = 9.4114, DKL = 0.3154
式を見れば,両者が線形にならないのは当然といえます.(以下,擬似コードを示します.)
重ならないエリアの面積が,
S = sum(abs(pk - qk), axis=0) * x_width
# pk - probability distribution 1
# qk - probability distribution 2
# x_width - width of discreted x points
であるのに対し,
DKLは,
DKL = sum(pk * log(pk / qk), axis=0)
# pk - probability distribution 1
# qk - probability distribution 2
ですので,SとDKLは線形の関係になりません.
次の例は,正規分布に skew をかけていった時の,DKLの変化を見たものです.
# Skewed normal distributions
fig, axes = plt.subplots(3, 3, figsize=(8, 8), sharey=True)
skew_opts = np.array([i * 0.1 for i in range(9)])
skew_opts = skew_opts.reshape([3, 3])
print('\n')
for i in range(3):
for j in range(3):
ax_ij = axes[i, j]
ax_ij.fill_between(px, pdf_std, py_zero, color='b', alpha=0.3)
pdf_ij = skewnorm.pdf(px, skew_opts[i, j], scale=1.)
ax_ij.fill_between(px, pdf_ij, py_zero, color='r', alpha=0.3)
ax_ij.set_xticklabels([])
dkl_ij = entropy(pdf_std, pdf_ij)
title_str = 'DKL={:>.3f}'.format(dkl_ij)
ax_ij.set_title(title_str)
# calculate area out-of-union
s = sum([abs(y1 - y2) for y1, y2 in zip(pdf_std, pdf_ij)])
print(' s = {:>.4f}, DKL = {:>.4f}'.format(s, dkl_ij))
Fig.2 Normal Distributions (skew added)
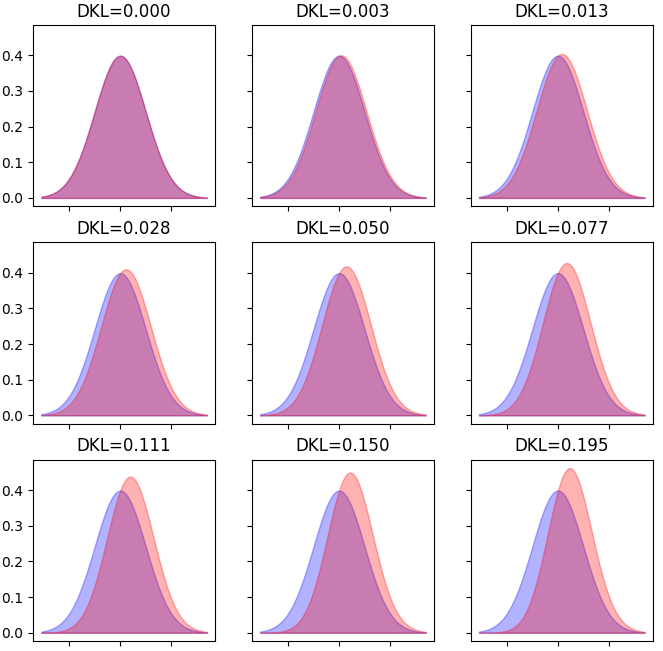
こちらも,重ならないエリアが大きくなるにつれ,DKLの値が大きくなることが確認できました.
いかがでしょうか? このように見てみると Kullback Leibler divergenceが大分理解できた気がするのではないでしょうか? 要は,生成したモデルと入力データから導出されたモデルの「近さ」を測るための指標です.
「GANって学習が難しいから,Kullback Leiblerをよくモニターする必要があるよね?」とか,
「Kullback Leiblerが振動的になるから,Learning Rateを調整しようかな?」などと
つぶやくことで,「こいつ,生成モデルに詳しい」感を,かもしだすことができるかも知れません.
(プログラミング環境は次の通りです:Python 3.5.2, Scipy 0.19.0, Matplotlib 2.0.0 )
参考文献, web site
- カルバック・ライブラー情報量
https://ja.wikipedia.org/wiki/%E3%82%AB%E3%83%AB%E3%83%90%E3%83%83%E3%82%AF%E3%83%BB%E3%83%A9%E3%82%A4%E3%83%96%E3%83%A9%E3%83%BC%E6%83%85%E5%A0%B1%E9%87%8F - Kullback–Leibler divergence
https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence - はじめてのパターン認識(第10章),平井氏 著,森北出版
https://www.morikita.co.jp/books/book/2235 - Scipy Documentation
https://docs.scipy.org/doc/scipy/reference/stats.html