(追記1)用語("in-sample", "out-of-sample")の使い方が不適切との指摘をいただきました.本記事の後半部にこの点,追記いたしました.
(追記2)を後半部に加えました.
Qiita投稿した後,内容の誤りに気がついても,手間を惜しんでそのままになってしまいがちである.ごく小さな誤記であればまだいいが,理論的な誤りや勘違いにおいては,間違った発信が続いていることには違いなく,反省しなければならない.(記事削除が手っ取り早いのですが,「いいね」がついていたりすると削除も失礼かと... )
さて,以前 回帰モデルの比較 - ARMA vs. Random Forest Regression - Qiita で時系列データからLag(遅れ)を特徴量として使う Random Forest回帰のやり方を紹介している.
今回は単変量の時系列データであるが,いくつかの過去のデータ使って現在の値を推定するモデルとしてみた.具体的には,
Volume_current ~ Volume_Lag1 + Volume_Lag2 + Volume_Lag3
というモデルである.訓練データとテストデータを前回と同じ(70, 30)にしたかったが,Lag値を計算する過程でNaNがでるので,初めの部分をdropna()して,(67, 30) のデータ長とした.
まず,データの前処理を行う.
df_nile['lag1'] = df_nile['volume'].shift(1)
df_nile['lag2'] = df_nile['volume'].shift(2)
df_nile['lag3'] = df_nile['volume'].shift(3)
df_nile = df_nile.dropna()
X_train = df_nile[['lag1', 'lag2', 'lag3']][:67].values
X_test = df_nile[['lag1', 'lag2', 'lag3']][67:].values
y_train = df_nile['volume'][:67].values
y_test = df_nile['volume'][67:].values
Scikit-learnのRandomForestRegressorを使用.
from sklearn.ensemble import RandomForestRegressor
r_forest = RandomForestRegressor(
n_estimators=100,
criterion='mse',
random_state=1,
n_jobs=-1
)
r_forest.fit(X_train, y_train)
y_train_pred = r_forest.predict(X_train)
y_test_pred = r_forest.predict(X_test)
機械学習の典型的な手続きに従い,データを訓練データ/テストデータに分割し,訓練データを用いてモデルをフィット,その後,モデル予測値とテストデータのラベルで答え合わせをするという流れである.さてどこが誤りなのか?図を用いて上コードの流れを説明する.
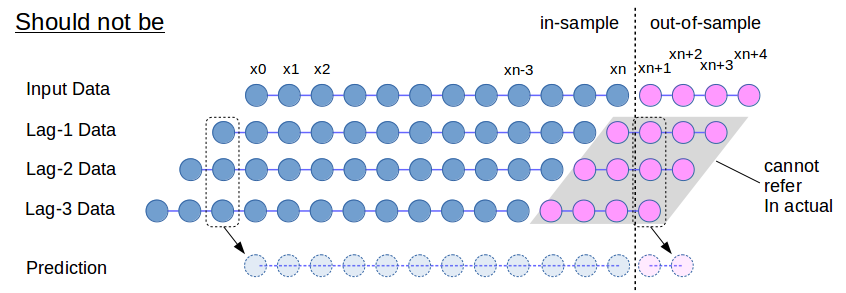
Fig.1 誤った時系列データの予測・検証のやり方
元の時系列データから pandas.DaraFrame.shift で3本のLagデータを生成する.その後,所定の時刻にて訓練データ(in-sample)とテストデータ(out-of-sample)に分割している.一見良さそうだが,この手続きにおいて元のデータ系列のテストデータ区間(ピンク色の部分)からLagデータの系列に組み込まれることになる.モデル検証ではこのような処理を行うことができるが,現実には所定時刻以降のデータ(out-of-sample) は未来の情報につき存在していないため,この処理は実施不可能である.
正しいやり方としては,データ予測に必要なLag値を一つ一つ埋めつつ,前に進めるのが適当.
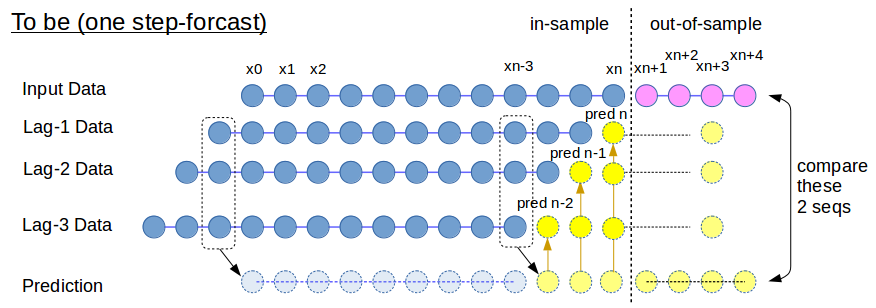
Fig.2 正しい時系列データの予測・検証のやり方
上図にて,ピンク色の情報は,検証(Validation)にて答え合わせとして除外する必要がある.時刻(xn-3)にて訓練データはすべて青色の in-sample データで揃えることができる.次の時刻(xn-2)では,Lag-3のデータが欠損するので,予測モデルを使ってここの値を算定する.次の時刻(xn-1)では,Lag-2, Lag-3の足りないところを埋める,といった計算プロセスになると考えられる.これをコードとしたのが以下.
def step_forward(rf_fitted, X, in_out_sep=67, pred_len=33):
# predict step by step
nlags = 3
idx = in_out_sep - nlags - 1
lags123 = np.asarray([X[idx, 0],
X[idx, 1],
X[idx, 2]])
x_pred_hist = []
for i in range(nlags + pred_len):
x_pred = rf_fitted.predict([lags123])
if i > nlags:
x_pred_hist.append(x_pred)
lags123[0] = lags123[1]
lags123[1] = lags123[2]
lags123[2] = x_pred
x_pred_np = np.asarray(x_pred_hist).squeeze()
return x_pred_np
上のコードにて rf_fitted は,回帰のfit(学習)が完了したRandom Forestモデルである.これを用いて,未来の値,out-of-sample にあたるところを1ステップずつ,計算している.
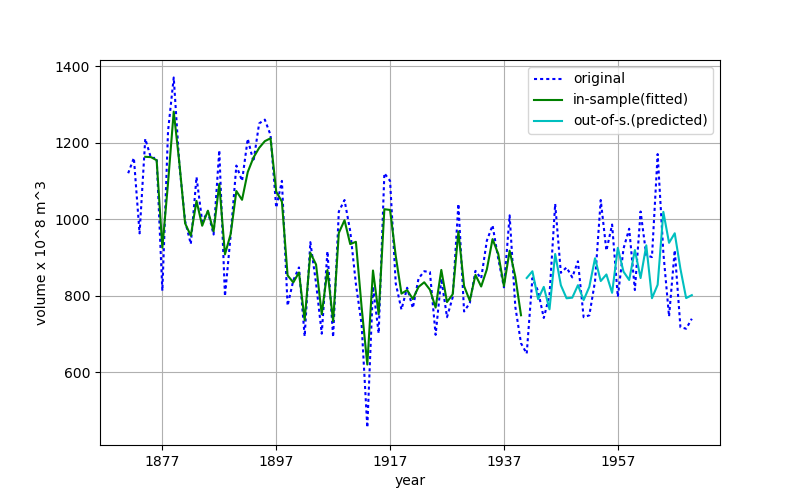
さて間違ったやり方/正しいやり方で予測値はどのように違うかを確認する.
シアン色で描かれる out-of-sample の線に着目すると,上図では本来参照してはいけない入力値(点線)の予測区間の高周波成分が,予測値(シアン色実線)にも反映されているように見える.但しこの区間での重なり具合は高く見えている.
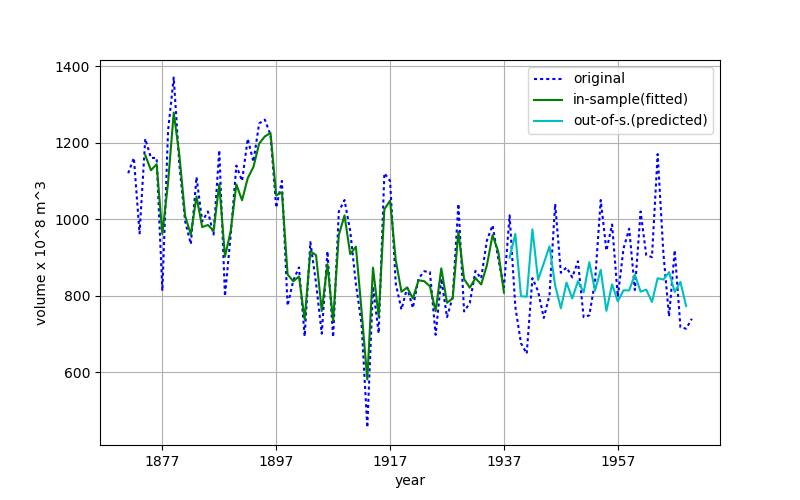
この図では予測区間の予測値高周波成分は,かなり小さく見えていて,区間後半では,実際の値(点線)とやや乖離しているように見える.しかし,in-sample 区間の「ゆるやかに減少している」という大きなトレンドをこの図では,out-of-sample予測値に見ることができる.(個人的な見方ですが... )
時系列データ解析では,このような落とし穴があることに気をつけたい.(普段から時系列データを扱っている方々にとっては基本中の基本なのかも知れませんが.)機械学習コンペサイト”Kaggle"等で時系列データを見つけて,少し実践的なところを勉強せねばと感じている.
また私の投稿記事に「いいね」をしてくれたり,「ストック」される方々も,記事の信頼性について考慮していただければと考えている.(間違っている可能性ありますという「おことわり」です.間違いにコメントいただけると,さらにうれしいと思います.)
参考文献,web site
- "Backtesting", "Walk Forward Optimization" - en.wikipedia
- How to split dataset for time-series prediction? - Cross Validated, StackExchange
https://stats.stackexchange.com/questions/117350/how-to-split-dataset-for-time-series-prediction
(追記1)用語 "in-sample", "out-of-sample" の定義について
本記事に対して,「in-sampleを「訓練データ」と同義に使っているがそういう意味ではないと思う.回帰の場合限定で「説明変数の値が訓練データと同じ」の意味」とのtweetをいただきました.ご指摘の通り,"in-sample"の理解があいまいでしたので,本記事の "in-sample" --> ”訓練データ”,"out-of-sample" --> ”テストデータ” と読み変えていただければと思います.上記用語のコンセプトについて,現時点でまだ十分理解しきれていないので,後日,記事を再更新させていただきます.
(追記2)用語 "in-sample" の定義について
記事の "in-sample" について調べましたので以下,参照下さい.
上記記事を書いた時,"in-sample" / "out-of-sample" という用語を時間軸上のある点で分け,その点までのデータを "in-sample",その点以降のデータを"out-of-sample"と考えていました.この使い方は不正確ではあるものの,このように用語が使われることは少なからずあるようです.
例えば,StackExchange, Cross Validated の質問,What is difference between “in-sample” and “out-of-sample” forecasts?には,回答として以下の説明が載っています.
if you use data 1990-2013 to fit the model and then you forecast for 2011-2013, it's in-sample forecast. but if you only use 1990-2010 for fitting the model and then you forecast 2011-2013, then its out-of-sample forecast.
用語の正確な「使い方」を文献 "The Elements of Statistical Learning, 2nd edition" で調べました.この本は,モデリング,機械学習の定番教科書で,ありがたいことにスタンフォード大学がFreeで配布しているものです.(私は「積ん読(どく)」ならぬ,ダウンロードしっぱなしになっていました...)
7章,"Model Assessment and Selection" 内の汎化性能,汎化誤差の説明にて "in-sample" が説明されていました.
Training set:
\mathcal{T} = \{ (x_1, y_1), (x_2, y_2), ...(x_N, y_N) \}
を用いて獲得したモデル "\hat{f}" で新規データ(Test data)を評価する場合,以下の汎化誤差(Generalization error)が生じます.
Err_{\mathcal{T}} = E_{X^0, Y^0} [L(Y^0,\ \hat{f}(X^0)) \mid \mathcal{T}] \\
汎化における精度低下はいろいろな要因がありますが,その中の一つが,データ点(説明変数)が訓練データとテストデータで異なることにあります.データ点が一致する場合は以下の"in-sample" 誤差となります.
Err_{in} = \frac{1}{N} \sum_{i=1}^{N} E_{Y^0} [L(Y^0_i ,\ \hat{f}(x_i)) \mid \mathcal{T} ]
断片的な引用につき説明が分かりにくいかと思いますが,上の2つの式を比べてください.着目すべきは,モデル式 "hat{f}" の引数で,一般的な "X^0" が下の式では "x_i" (訓練データのx) となっています.このようなデータが "in-samle" dataとなります.以下,図にします.
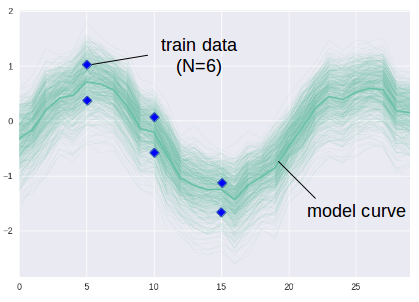
6点から成る訓練データ(Train data)からモデル(濃い線)が得られたケースを考えます.(実際に6点で線のようなsine curveが得られるわけではありません.説明図ということで理解願います.)
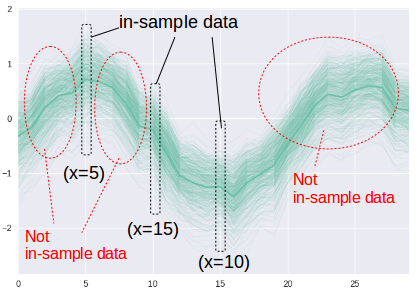
この訓練データとx値が一致するものが,"in-sample" データとなります.今回,訓練データは,x=5, 10, 15でしたので,これと一致しないものは "in-sample"ではありません.よってx軸上の x > 20 のデータは違いますし,加えて x=4, 7 などのすき間の点も "in-sample"ではないわけです.最初に StackExchange, Cross Validated の引用が正確ではない,というのはこの点にあります.但し,よく行われる時系列分析では,データ点が一定の間隔であることが多く(例えば,daily, monthly),この場合,時間軸上のある点で区切っても "in-sample"/それ以外に分割できるので,元の用語の定義に合致するという事情があります.
この用語の使い方の誤解以外の本文中の説明内容,時系列データ分析の処理については,現時点で間違っていないと思いますのでご確認ください.
「おいしいものが食べられる」「おいしいものが食べれる」のように言葉の使い方は変化していきますが,「技術用語は正確に使いましょう」ということで,今回の件は教訓になりました.