はじめに
推薦システムに用いられる協調フィルタリングは,機械学習の一つの応用例であるが,単純な「教師あり学習」のパターンと少し異なるところがある.文献,Internet情報を少しあたってみたが,概念,システム構成についてすぐに理解するのは難しい.しかし,Andrew Ng先生によるCoursera Machine Learning (week 9)で取り扱われていることを思い出し,その教材を復習することで協調フィルタリングについて理解を深めることができた.
受講された方はご存知と思われるが,このコースの演習では Matlab/Octave を用いている.今回は,Pythonで協調フィルタリング(の原型)を実装してみた.初めにNumpy+Scipy(Optimize)で動作を確認し,次にTensorFlowを用いた実装を確認した.
協調フィルタリングの概要を少し
データサイエンティスト養成読本,機械学習入門編から引用する.
協調フィルタリングはECサイトにおける次のような提示を実現する手法です.
- 「この商品を買った人はこんな商品も買っています.」
- 「あなたと同じ商品を買っている人はこんな商品も買っています.」
概念を理解できたところで実装であるが,Coursera Machine Learningでの解説を確認していく.
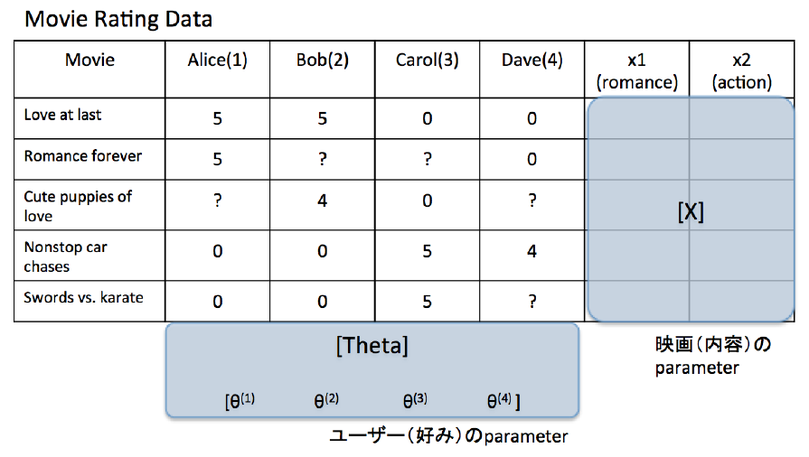
ここでは,映画ランキングの例を用いて説明を進めている.
表は,各ユーザによる映画のレーティングであるが,ユーザの好みに従って評価が分かれてくる.映画の内容に応じて,「ラブロマンスの傾向が強い」「アクション性が高い」等,ことなる尺度(Coursera授業ではメジャーといっていた)のパラメータであるデータ[X]が準備される.一方で「ユーザの好み」に対するパラメータ[Theta]も必要となる.図のようにレーティングのデータは,サイズが,映画数 x ユーザ数の2次元マトリクス([Y])であるが,ユーザがすべての映画にレートつけるわけではないので,不定となっているところが多い.この不定?マークのところを,回帰によって補完するというのが問題の主旨である.
補完できたレーティングのマトリクスが精度よく計算できれば,類似映画を推薦する次のプロセスにおける処理も上手にできるという説明である.
Numpy+Scipy.Optimizeで実装してみる
Couseraコースでの他の演習と同様,まずコスト関数を求めるところからスタートする.パラメータが2つあるので,かなり"ごつい"式となる.
\begin{eqnarray}
J(x^{(1)},...,x^{n_m},\theta^{1},...,\theta^{n_u}) = &\ & \frac{1}{2} \sum_{(i,j):r(i,j)=1}
(({\theta}^{(j)})^T \ x^{(i)} - y^{(i,j)})^2 \ + \\
&\ & (\frac{\lambda}{2} \sum_{j=1}^{n_u} \sum_{k=1}^{n} ({\theta}_k^{(j)}) ^2)
+ (\frac{\lambda}{2} \sum_{i=1}^{n_m} \sum_{k=1}^{n} ({x}_k^{(i)}) ^2)
\end{eqnarray}
パラメータ[X], [Theta]を持つコスト関数は,パラメータのマトリクス積で決まるレーティング予測値とレーティング実データ(ラベル)との二乗誤差,及びパラメータのregularization項から成る.これをPythonのコードに直すと以下のようになる.
def cofi_costfunc(Y, R, shapes, lambda_c, params):
# [J, grad] = COFICOSTFUNC(params, Y, R, num_users, num_movies, ...
# num_features, lambda) returns the cost and gradient for the
# collaborative filtering problem.
num_users = shapes[0]
num_movies = shapes[1]
num_features = shapes[2]
boundary = num_movies * num_features
params_c1 = np.copy(params[:boundary])
params_c2 = np.copy(params[boundary:])
X = params_c1.reshape((num_movies, num_features))
Theta = params_c2.reshape((num_users, num_features))
# You need to return the following values correctly
Jcost = 0.5 * (((np.dot(X, Theta.T) - Y) * R) ** 2).sum() \
+ 0.5 * lambda_c * ((X.ravel() **2).sum() + (Theta.ravel() **2).sum())
return Jcost
パラメータX(映画内容のパラメータ), Theta(ユーザ指向のパラメータ)は,一つのかたまりparamsで入力される.Yは,映画数 x ユーザ数の形のレーティング・データ.Rは,Y同じサイズで,レーティングがつけれているときに1,レーディングがまだない場合に0がセットされる,バイナリーのデータ.(プログラムの変数型としては, 整数型で扱っています.)前処理の後,上述のコスト関数式に対応してコストを求めているのが最後のステートメントである.
次にこのコスト関数のパラメータ(x,theta)に関する偏微分係数(勾配)の式である.
\frac{\partial J}{\partial x_k^{(i)}} = \sum_{j:r(i,j)=1} (( {\theta}^{(j)})^T x^{(i)}
- y^{(i,j)} ) {\theta}_k^{(j)} + \lambda x_k^{(i)}\\
\frac{\partial J}{\partial {\theta}_k^{(j)}} = \sum_{i:r(i,j)=1} (( {\theta}^{(j)})^T x^{(i)}
- y^{(i,j)} ) {x}_k^{(i)} + \lambda {\theta}_k^{(j)}
こちらもそれなりに"ごつい"数式である.しかし,コードに直すと理解しやすい.
def cofi_costfunc_grad(Y, R, shapes, lambda_c, params):
# [J, grad] = COFICOSTFUNC(params, Y, R, num_users, num_movies, ...
# num_features, lambda) returns the cost and gradient for the
# collaborative filtering problem.
num_users = shapes[0]
num_movies = shapes[1]
num_features = shapes[2]
boundary = num_movies * num_features
params_c1 = np.copy(params[:boundary])
params_c2 = np.copy(params[boundary:])
X = params_c1.reshape((num_movies, num_features))
Theta = params_c2.reshape((num_users, num_features))
# You need to return the following values correctly
X_grad = np.dot(((np.dot(X, Theta.T) - Y) * R), Theta) + lambda_c * X
Tgsub = (np.dot(X, Theta.T) - Y) * R
Theta_grad = np.dot(Tgsub.T, X) + lambda_c * Theta
Jgrad = np.concatenate((X_grad.ravel(), Theta_grad.ravel()))
return Jgrad
後半の4行にて,コスト勾配を算出している.
Courseraの演習では,コスト最小化の最適化プロセスを,事前に用意して提供される fmincg.m の関数を用いて行っている.Pythonに直す場合は同様の処理を scipy.optimize.minimize() で行うことができる.
#
import scipy.optimize as spopt
# パラメータの初期値をセット
theta_ini = np.concatenate((X.flatten(), Theta.flatten()))
# wrapper 関数を用意
def compute_cost_sp(theta):
global Y, R, shapes, lambda_c
j = cofi_costfunc(Y, R, shapes, lambda_c, params=theta)
return j
def compute_grad_sp(theta):
global Y, R, shapes, lambda_c
j_grad = cofi_costfunc_grad(Y, R, shapes, lambda_c, params=theta)
return j_grad
# scipy.optimize.minimize のオプションをセット
options = {'gtol': 1.e-6, 'disp': True}
# Regularization係数
lambda_c = 1.5
res1 = spopt.minimize(compute_cost_sp, theta_ini, method='CG', \
jac=compute_grad_sp, options=options)
theta = res1.x
# ひとかたまりのパラメータをXとThetaに分解
X = theta[:num_movies*num_features].reshape((num_movies, num_features))
Theta = theta[num_movies*num_features:].reshape((num_users, num_features))
scipy.optimize.minimize の詳細についてはドキュメントを参照していただきたいが,最適化手法としていろいろなものを選択することができる.今回は元ネタ(fmincg.m)に合わせ method='CG' (Conjugate gradient method) とした.
このようにコスト最小化を行って求めたパラメータ [X], [Theta] から,必要な情報(ex. 「この映画に高い評価をした人は,別のこの映画の評価も高いです.」)を取り出すのが推薦システムの処理となる.(類似度を測るやり方にいろいろあるようですが,ここでは説明を省略いたします.)
TensorFlowを使う
昨年(2015年)にTensorFlowが公開されてから約一年が立つ.わくわくしながらコードを作成し,急いでQiita投稿記事を書いた記憶がある.今回,協調フィルタリングの学習をより高速な処理で実行させるにあたり,TensorFlowを使うことにした.
通常の「教師あり学習」であれば,入力-出力の関係が明確なので,TensorFlowのグラフ表現に迷うことはないのだが,今回は少し難しかった.
- 通常の問題で,重み w,バイアス b にあたるもの ... 今回は 映画内容のパラメータ x とユーザの好みのパラメータ Theta.
- 通常の問題で,教師データにあたるもの ... 今回は,事前にユーザがつけたレーティングの情報.具体的には,データ Y(ユーザが映画につけたレーティングを包有する 映画数 x ユーザ数のマトリクス)と R(ユーザがレーティングをしたか/していないかを示すバイナリーデータ).
よって,変数準備のコードは次のようなものとした.
# Parameter definition
if WARM_START:
data_param = load_data(fn='./data/ex8_movieParams.mat')
X_np = data_param['X'].astype(np.float32)
Theta_np = data_param['Theta'].astype(np.float32)
x = tf.Variable(X_np)
theta = tf.Variable(Theta_np)
else: # COLD START
x = tf.Variable(tf.random_normal([num_movies, num_features],
mean=0.0, stddev=0.05))
theta = tf.Variable(tf.random_normal([num_users, num_features],
mean=0.0, stddev=0.05))
# Placeholders
Y_ph = tf.placeholder(tf.float32, shape=[None, num_users])
R_ph = tf.placeholder(tf.float32, shape=[None, num_users])
Courseraのプログラム演習で,ある程度の事前学習が行われていたパラメータのデータが提供されているので,それを用いる 'WARM_START' のオプションとゼロからのスタートを行うオプションを用意した.'WARM_START' では,numpy.array のデータをそのまま tf.Variable() に渡すだけ,ゼロスタートの場合は,小さい値となる乱数を発生させてx,thetaにセットする.また,教師データのplaceholderは,必要なshapeのものを用意した.
(shape=[None, num_users] は,shape=[num_movies, num_users]でも問題ないと思いますが,TensorFlowの慣例に従いNoneとしています.)
次にコスト関数の計算を定義する.
def Ypred(X, Theta):
'''
calculate rating with parameter X and Theta
args.:
X: movie contents parameter
Theta: user characteristic parameter
'''
feat_dim1 = tf.shape(X)[1]
feat_dim2 = tf.shape(Theta)[1]
tf.assert_equal(feat_dim1, feat_dim2)
rating = tf.matmul(X, tf.transpose(Theta))
return rating
# Cost Function, etc.
cost = tf.reduce_sum(((Ypred(x, theta) - Y_ph) * R_ph) ** 2)
L2_sqr = tf.nn.l2_loss(x) + tf.nn.l2_loss(theta)
lambda_c = 1.0 # L2 norm coefficient
loss = cost + lambda_c * L2_sqr
TensorFlowだけではないが,Deep Learningフレームワークの便利なところはGradientを自動計算してくれるところである.上記のようにコスト関数のみの定義で済むのが「えらい」と感じる.この後,例によってオプティマイザをセットして学習ループとなる.
lr = 1.e-5
train_step = tf.train.GradientDescentOptimizer(lr).minimize(loss)
init_op = tf.initialize_all_variables()
# Train
with tf.Session() as sess:
sess.run(init_op)
for i in range(10001):
sess.run(train_step, feed_dict={Y_ph: Y_np, R_ph: Y_np})
if i % 1000 == 0:
loss_mon = loss.eval({Y_ph: Y_np, R_ph: Y_np})
print(' step, loss = {:6d}: {:10.1f}'.format(i, loss_mon))
# evaluate ranking with final parameters
ymat = Ypred(x, theta).eval()
sio.savemat('./ymat_tf.mat', {'Y': ymat})
print('ymat is saved to "ymat_tf.mat".')
別に tf.train.GradientDescentOptimizer() でなくても好きなオプティマイザを使えばいいと思うが,今回は Cousera の課題ということで,基本的な関数を用いてみた.学習率の調整にやや手間がかかるが,無事に(gpu演算で高速に)計算を行うことができた.
結果比較
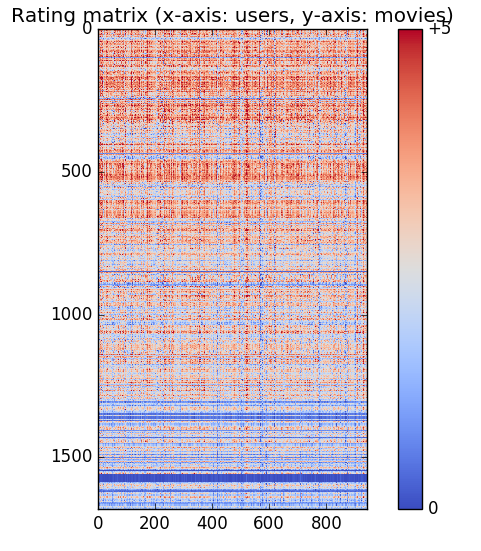
同じアルゴリズムで解いているので,scipy.optimize.minimize によるものとTensorFlowによる結果は同様なものとなるはずである.今回は,求めたパラメータ(X, Theta) からレーティング・マトリクス Y を計算しこれをHeatmap図のようにしてみた.(青:低いレート 〜 赤:高いレート)
By scipy.optimize.minimize
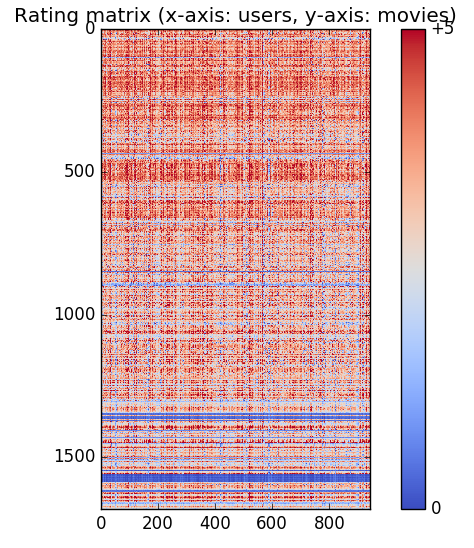
By TensorFLow
詳細部に色の濃淡などの違いが見られるが,大きなパターンとしては同様なものに見ることができる.計算プロセスとしては,問題なしと思われる.
両者の違いを埋めようとするなら,Regularization,学習率,収束状況等,細かいところを調整する必要がある.「協調フィルタリングを学ぶ」をいう目的では以上の内容でOKと思うが,Kaggle等コンペで戦うためには,いろいろ詳細を検討しなければならないだろう.
(今回用いたプログラミング環境は,次のようになります.Python 3.5.2, Numpy 1.11.2, Scipy 0.18.1, TensorFlow 0.11.0 )
(コードをGistにUpしました: https://gist.github.com/tomokishii/2e9f83d391df82f25942c1310b41e0b5 )
参考文献,web site
- Cousera, Machine Learning, by Prof.Andrew Ng(毎週,プログラミング課題の説明書/PDFが配布されます.受講終了後もサイトにて,教材ビデオ,プログラミング演習の関連ファイルにアクセス可能です.)
- データサイエンティスト養成読本,機械学習入門編(第2部特集3),推薦システム入門
http://gihyo.jp/book/2015/978-4-7741-7631-4 - pythonでアイテムベース協調フィルタリングを実装する - MovieLensを例に - Qiita
http://qiita.com/kotaroito/items/6acb58bb16b68a460af9 - 実践 機械学習システム - オライリー・ジャパン,8章 回帰:レコメンドの改良
http://www.oreilly.co.jp/books/9784873116983/ - Scipy Documentation
https://docs.scipy.org/doc/scipy-0.18.1/reference/generated/scipy.optimize.minimize.html