オセロのAIアルゴリズムをディープラーニングで作成し、私が勝てないぐらいまでには強くなった、という話です。
また私の場合は2ヶ月ぐらいかかってしまいましたが、実装自体はそんなに難しくなかったので、実装方法についても説明したいと思います。
この記事でわかることは、ディープラーニングでオセロのAIアルゴリズムを作る方法です。基本的な考え方は他のボードゲームも同じなので、流用できると思います。
対象読者は、TensorFlowなどディープラーニングのライブラリを使い始めて、MNISTの数字分類など基本的な処理はできたけれど、それ以外の問題だとやり方がわからない、というような方です。
きっかけ
私の所属するエンジニアと人生コミュニティで、リバーシチャレンジなるものが開催されたことがきっかけです。このコンテストは「リバーシならどこにこだわっても良い」というルールでした。
私は、ちょうど少しまえに「将棋AIで学ぶディープラーニング」という本を読んでいて、いつかボードゲームのAIを作ってみたいなと思っていたところだったので、エントリーすることにしました。
わりと気楽にエントリーして、ディープラーニングのモデルを簡単に作ってAIに打たせてみよう、ぐらいの気持ちからスタートしたのですが、途中からだんだん「自分に勝つぐらいにしたい」と思い始めて、改善をしていったのでした。
私のオセロの腕について
「自分を負かしたっていっても、あなたのオセロの腕はどうなのよ?」という疑問もあると思います。
ハッキリ言えば弱いです。
ディープラーニングと対戦を繰り返す中で私も少しずつ強くなりましたが、だいたいこんなことを考えて打っています。
(私の思考)
- 最初は真ん中あたりの4x4マスから抜けないように打つと良さそう
- 盤面の端にあるマスは取られづらいからなるべく取りたい
- 四隅は絶対に取られないので、なんとしても取りたい
- 先読みは面倒だからしない
出来たもの
モデルの作成と訓練はTensorFlowを使いましたが、最終的にはiOSアプリ(AppStoreには出していません)になりました。GitHubからcloneすれば手元で動かすことができます。
TokyoYoshida/reversi-charenge

機能としては、AIと対戦できるほか、メンテナンスモードにすると自由に盤面を作ることができます。勝ち負けの判定機能は作っていないので、最後に自分の石の数を数える必要があります。
AIの強さは、だいたい私と対戦して8割ぐらいはAIが勝つぐらいです。なぜかたまに私が自分の石の色だけになる完全勝利をすることもあります。理由は不明ですが、このAIは先読みしないのと、後半まで自分の石をあまり増やさずに最後に追い上げる傾向があることが関係しているのかもしれません。
対戦結果の例
私が黒、AIが白です。
対戦していくうちに、四隅だけを取ろうとしても必ずしも勝てないことや、あまり自分の石が多すぎると、パスしかできなくなってしまうことがあることがわかりました。
作り方の概要
作り方の説明に入っていきます。
盤面のデータを画像として渡すと、次に打つ手を予想してくれるようなニューラルネットのモデルを作り、訓練することでオセロAIを作ることができます。
「次の手の予想」とは、オセロは8x8マスあるので「64マスのどこが最善かを予想する分類問題」ということになります。
 **※画像といってもピクセルデータではなく盤面を表現した配列です**
**※画像といってもピクセルデータではなく盤面を表現した配列です**
これは、AlphaGoのSLポリシーネットワークの仕組みを模したもので、教師あり学習を使って棋譜データから盤面の画像とその時に打った手をニューラルネットに学習させることで、盤面を与えると次の手を予想してくれるようになるというものです。
AlphaGoの場合はさらに様々な手法を組み合わせていますが、今回はSLポリシーネットワークだけを作りました。おまけとしてモンテカルロ木探索も組み合わせたものも作りましたが、これはAlphaGoとはだいぶ異なる方法になっています。
参考:
AlphaGoの論文(原題:Mastering the game of Go with deep neural networks and tree search)
AlphaGoを模したオセロAIを作る(1): SLポリシーネットワーク
作り方の手順は次のとおりです。
1.学習データを作る
2.モデルを作る
3.訓練する
----(今回の説明はここまで)----
4.UIを作る(ついでにモンテカルロ木探索をする)
本記事はその1なので訓練するところまでの説明ですが、オセロの手をAIに予想させるところまでは作ります。
また、実装はPythonを使いGoogle Colaboratory上で動作させていますが、Pythonが動作する環境なら何でも良いです。
1.学習データを作る
これが一番大変な作業だったりします。1つ1つ説明します。
・棋譜データをダウンロードする
学習データは、フランスのオセロ連盟が公開しているオセロの棋譜データベースWTHORを使うので、データをダウンロードしておきます。
・棋譜データをcsvに変換する
ダウンロードした棋譜データはバイナリフォーマットになっているため、これを変換用サイトでcsvに変換します。出力形式を選べますが今回は「全項目出力」を使いました。
参考:オセロの棋譜データベースWTHORの読み込み方
(このツールを作った方の記事です。)
棋譜データをcsvに変換したら、1つのファイルにマージします。
・csvデータをデコードする
データセットをcsvで読み込み、ヘッダ行を削除します。
import pandas as pd
import re
import numpy as np
# csvの読み込み
df = pd.read_csv("wthor棋譜データ.csv")
# ヘッダ行の削除
df = df.drop(index=df[df["transcript"].str.contains('transcript')].index)
読み込んだデータのうち、transcriptという列が実際の棋譜の情報です。
文字列が並んでいるのが分かりますが、1つの列値が1試合分のデータとなっています。

文字列はf5f6e6・・・と続いていますが、2文字で1手となっていて次のようにエンコードされています。
1文字目 ・・・ 列(a,b,c・・・h)
2文字目 ・・・ 行(1,2,3・・・8)
例えばf5なら、左から6列目、上から5行目ということです。
このままtranscriptに1試合のデータがすべて入っているのは分かりづらいので、
1行=1手となるように展開します。あわせて、文字列をデコードして列番号と行番号に変換します。
# 正規表現を使って2文字ずつ切り出す
transcripts_raw = df["transcript"].str.extractall('(..)')
# Indexを再構成して、1行1手の表にする
transcripts_df = transcripts_raw.reset_index().rename(columns={"level_0":"tournamentId" , "match":"move_no", 0:"move_str"})
# 列の値を数字に変換するdictonaryを作る
def left_build_conv_table():
left_table = ["a","b","c","d","e","f","g","h"]
left_conv_table = {}
n = 1
for t in left_table:
left_conv_table[t] = n
n = n + 1
return left_conv_table
left_conv_table = left_build_conv_table()
# dictionaryを使って列の値を数字に変換する
def left_convert_colmn_str(col_str):
return left_conv_table[col_str]
# 1手を数値に変換する
def convert_move(v):
l = left_convert_colmn_str(v[:1]) # 列の値を変換する
r = int(v[1:]) # 行の値を変換する
return np.array([l - 1, r - 1], dtype='int8')
transcripts_df["move"] = transcripts_df.apply(lambda x: convert_move(x["move_str"]), axis=1)
・棋譜データを学習データに変換する
1手1手のデータを盤面に展開して学習の入力データにします。
学習データは、入力データとしてオセロの盤面、教師データとしてその時の1手です。
たとえば、最初の例にあるオセロの盤面を学習データにした場合は、次の図のようになります。
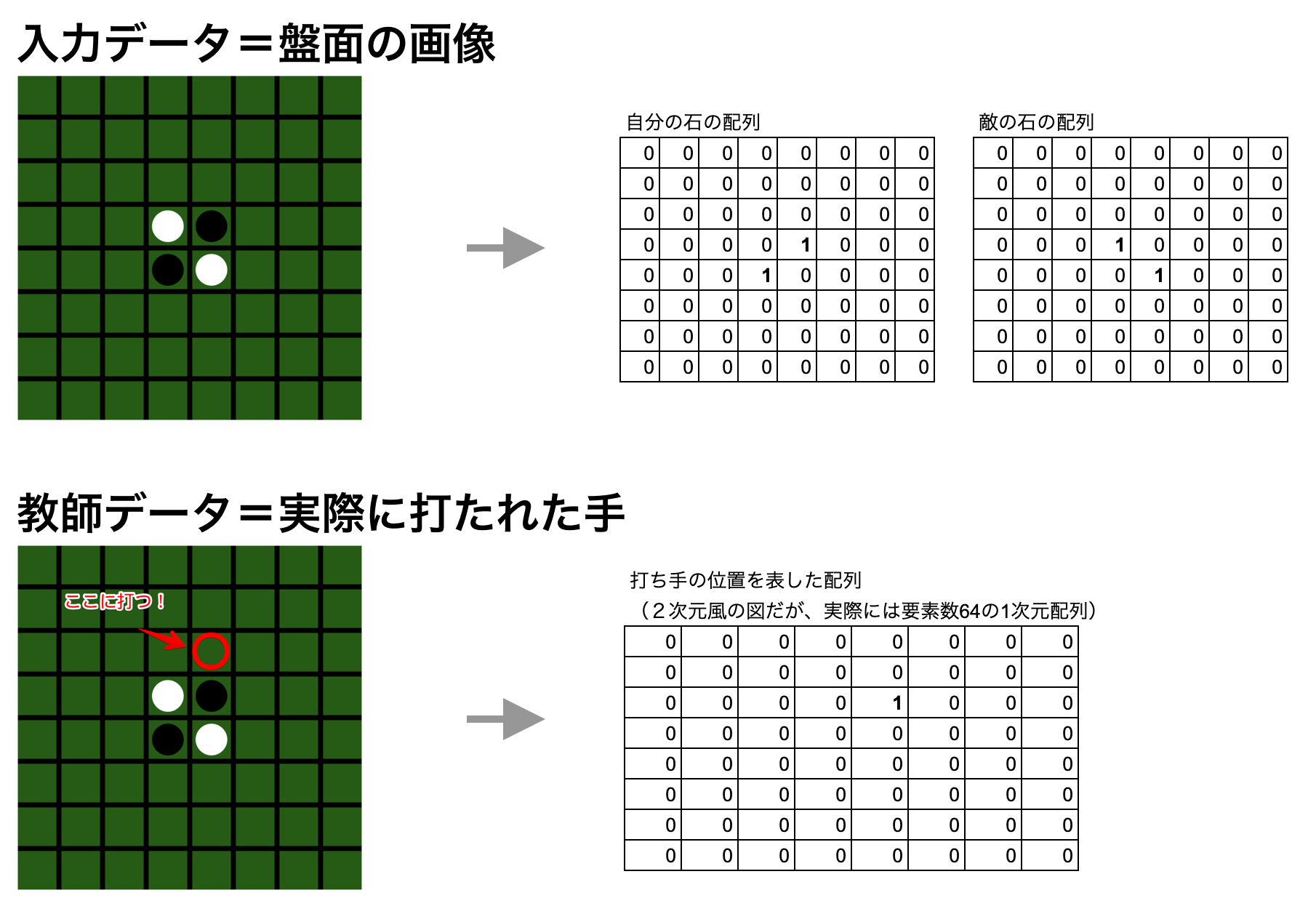
shapeは、それぞれ次のようになります。
学習データ = (バッチ数, 2(チャンネル。自分の石の配置と敵の石の配置), 8(行), 8(列))
予想データ = (バッチ数, 64(8x8の盤面の位置で左上が0番目で右下が63番目))
注意点は、入力データのチャンネルは黒→白という並びではなく、自分の石→敵の石という並びになっていることです。このようにすることで、黒が打ったデータも、白が打ったデータもこの並び方に従っていれば学習データとして利用できるようにしています。
盤面に展開するためには、1手を打ったら敵の石をひっくり返す処理を入れて、その時の盤面を記録していきます。
パスの場合は次のデータも同じプレイヤーの手になります。単純に黒の番、白の番、、と交互に読んでしまうと盤面がおかしくなるのでパスの時の判定処理を入れます。
# 盤面の中にあるかどうかを確認する
def is_in_board(cur):
return cur >= 0 and cur <= 7
# ある方向(direction)に対して石を置き、可能なら敵の石を反転させる
def put_for_one_move(board_a, board_b, move_row, move_col, direction):
board_a[move_row][move_col] = 1
tmp_a = board_a.copy()
tmp_b = board_b.copy()
cur_row = move_row
cur_col = move_col
cur_row += direction[0]
cur_col += direction[1]
reverse_cnt = 0
while is_in_board(cur_row) and is_in_board(cur_col):
if tmp_b[cur_row][cur_col] == 1: # 反転させる
tmp_a[cur_row][cur_col] = 1
tmp_b[cur_row][cur_col] = 0
cur_row += direction[0]
cur_col += direction[1]
reverse_cnt += 1
elif tmp_a[cur_row][cur_col] == 1:
return tmp_a, tmp_b, reverse_cnt
else:
return board_a, board_b, reverse_cnt
return board_a, board_b, reverse_cnt
# 方向の定義(配列の要素は←、↖、↑、➚、→、➘、↓、↙に対応している)
directions = [[-1,0],[-1,1],[0,1],[1,1],[1,0],[1,-1],[0,-1],[-1,-1]]
# ある位置に石を置く。すべての方向に対して可能なら敵の石を反転させる
def put(board_a, board_b ,move_row, move_col):
tmp_a = board_a.copy()
tmp_b = board_b.copy()
global directions
reverse_cnt_amount = 0
for d in directions:
board_a ,board_b, reverse_cnt = put_for_one_move(board_a, board_b, move_row, move_col, d)
reverse_cnt_amount += reverse_cnt
return board_a , board_b, reverse_cnt_amount
# 盤面の位置に石がないことを確認する
def is_none_state(board_a, board_b, cur_row, cur_col):
return board_a[cur_row][cur_col] == 0 and board_b[cur_row][cur_col] == 0
# 盤面に石が置けるかを確認する(ルールでは敵の石を反転できるような位置にしか石を置けない)
def can_put(board_a, board_b, cur_row, cur_col):
copy_board_a = board_a.copy()
copy_board_b = board_b.copy()
_, _, reverse_cnt_amount = put(copy_board_a, copy_board_b, cur_row, cur_col)
return reverse_cnt_amount > 0
# パスする必要のある盤面かを確認する
def is_pass(is_black_turn, board_black, board_white):
if is_black_turn:
own = board_black
opponent = board_white
else:
own = board_white
opponent = board_black
for cur_row in range(8):
for cur_col in range(8):
if is_none_state(own, opponent, cur_row, cur_col) and can_put(own, opponent, cur_row, cur_col):
return False
return True
# 変数の初期化
b_tournamentId = -1 # トーナメント番号
board_black = [] # 黒にとっての盤面の状態(1試合保存用)
board_white = [] # 白にとっての盤面の状態(1試合保存用)
boards_black = [] # 黒にとっての盤面の状態(全トーナメント保存用)
boards_white = [] # 白にとっての盤面の状態(全トーナメント保存用)
moves_black = [] # 黒の打ち手(全トーナメント保存用)
moves_white = [] # 白の打ち手(全トーナメント保存用)
is_black_turn = True # True = 黒の番、 False = 白の番
# ターン(黒の番 or 白の番)を切り変える
def switch_turn(is_black_turn):
return is_black_turn == False # ターンを切り替え
# 棋譜のデータを1つ読み、学習用データを作成する関数
def process_tournament(df):
global is_black_turn
global b_tournamentId
global boards_white
global boards_black
global board_white
global board_black
global moves_white
global moves_black
if df["tournamentId"] != b_tournamentId:
# トーナメントが切り替わったら盤面を初期状態にする
b_tournamentId = df["tournamentId"]
board_black = np.zeros(shape=(8,8), dtype='int8')
board_black[3][4] = 1
board_black[4][3] = 1
board_white = np.zeros(shape=(8,8), dtype='int8')
board_white[3][3] = 1
board_white[4][4] = 1
is_black_turn = True
else:
# ターンを切り替える
is_black_turn = switch_turn(is_black_turn)
if is_pass(is_black_turn, board_black, board_white): # パスすべき状態か確認する
is_black_turn = switch_turn(is_black_turn) #パスすべき状態の場合はターンを切り替える
# 黒の番なら黒の盤面の状態を保存する、白の番なら白の盤面の状態を保存する
if is_black_turn:
boards_black.append(np.array([board_black.copy(), board_white.copy()], dtype='int8'))
else:
boards_white.append(np.array([board_white.copy(), board_black.copy()], dtype='int8'))
# 打ち手を取得する
move = df["move"]
move_one_hot = np.zeros(shape=(8,8), dtype='int8')
move_one_hot[move[1]][move[0]] = 1
# 黒の番なら自分→敵の配列の並びをを黒→白にして打ち手をセットする。白の番なら白→黒の順にして打ち手をセットする
if is_black_turn:
moves_black.append(move_one_hot)
board_black, board_white, _ = put(board_black, board_white, move[1], move[0])
else:
moves_white.append(move_one_hot)
board_white, board_black, _ = put(board_white, board_black, move[1], move[0])
# 棋譜データを学習データに展開する
transcripts_df.apply(lambda x: process_tournament(x), axis= 1)
上のコードを実行したとき、各変数は次のような状態になっています。
boards_black ・・・ 黒が手を打つ直前の盤面の状態
boards_white ・・・ 白が手を打つ直前の盤面の状態
moves_black ・・・ 黒が打った手
moves_white ・・・ 白が打った手
これらを使って学習データを作ります。
黒と白の盤面と打ち手をつなげて1つのデータにするだけです。
x_train = np.concatenate([boards_black, boards_white])
y_train = np.concatenate([moves_black, moves_white])
# 教師データは8x8の2次元データになっているので、64要素の1次元データにreshapeする
y_train_reshape = y_train.reshape(-1,64)
学習データが出来ました。
私はWTHORから20年分のデータをダウンロードしてこの処理をしましたが、535万盤面のデータになりました。まだダウンロードしていないデータも合わせるとさらに強いAIが作れるはずです。
2.モデルを作る
いよいよモデルを作ります。
入力データは、上で説明したとおりshape=(バッチ数,2,8,8)の配列です。これを先頭でPermute(転置)をしていますがこれはTensorFlowの都合です。Conv2DにChannels First(batch, C, H, W)と指定すれば大丈夫だろうと思っていたらなぜかConv2DがChannels Firstを受け付けてくれなかったので、急きょChannels Last(batch, H, W, C)に変換しています。(これがわかっていたら最初からそういうデータを用意すればよかったです..)
続けて、カーネルサイズ3の畳み込み層を12層と、カーネルサイズ1の畳み込み層、最後にバイアス層を入れてSoftMax関数にかけています。結果として出力はshape=(バッチ数,64)の配列になります。64の要素にはオセロのマスごとに次の手の確率が0〜1の数字で入ります。1に近いほど良い手ということになります。
バイアス層ですが、tf.kerasにはバイアス層がなかったのでBiasクラスとして自作しています。
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from keras.engine.topology import Layer
class Bias(keras.layers.Layer):
def __init__(self, input_shape):
super(Bias, self).__init__()
self.W = tf.Variable(initial_value=tf.zeros(input_shape[1:]), trainable=True)
def call(self, inputs):
return inputs + self.W
model = keras.Sequential()
model.add(layers.Permute((2,3,1), input_shape=(2,8,8)))
model.add(layers.Conv2D(128, kernel_size=3,padding='same',activation='relu'))
model.add(layers.Conv2D(128, kernel_size=3,padding='same',activation='relu'))
model.add(layers.Conv2D(128, kernel_size=3,padding='same',activation='relu'))
model.add(layers.Conv2D(128, kernel_size=3,padding='same',activation='relu'))
model.add(layers.Conv2D(128, kernel_size=3,padding='same',activation='relu'))
model.add(layers.Conv2D(128, kernel_size=3,padding='same',activation='relu'))
model.add(layers.Conv2D(128, kernel_size=3,padding='same',activation='relu'))
model.add(layers.Conv2D(128, kernel_size=3,padding='same',activation='relu'))
model.add(layers.Conv2D(128, kernel_size=3,padding='same',activation='relu'))
model.add(layers.Conv2D(128, kernel_size=3,padding='same',activation='relu'))
model.add(layers.Conv2D(128, kernel_size=3,padding='same',activation='relu'))
model.add(layers.Conv2D(128, kernel_size=3,padding='same',activation='relu'))
model.add(layers.Conv2D(1, kernel_size=1,use_bias=False))
model.add(layers.Flatten())
model.add(Bias((1, 64)))
model.add(layers.Activation('softmax'))
モデルが出来たらコンパイルをします。
オプティマイザはAlphaGoと同じSGD、損失関数は分類問題なので、categorical_crossentropyを使用します。
model.compile(keras.optimizers.SGD(lr=0.01, momentum=0.0, decay=0.0, nesterov=False), 'categorical_crossentropy', metrics=['accuracy'])
3.訓練する
訓練をします。
訓練は、Google Colabだとタイムアウトが厳しいので、Google AI Platformのインスタンス上で実行しました。try〜exceptで囲って途中で中断しても学習したモデルを保存するようにしてあります。
このあたりのことは、Google Colaboratoryで利用していたノートブックをGoogle AI Platformで実行し、さらにコマンドラインからも実行する方法にまとめてあります。
try:
model.fit(x_train, y_train_reshape, epochs=600, batch_size=32, validation_split=0.2)
except KeyboardInterrupt:
model.save('saved_model_reversi/my_model')
print('Output saved')
AI Platformのインスタンス(NVIDIA Tesla T4 GPU)で、6時間ほど学習して4エポックほど学習したところ、val_accuracyが0.59になったので、そこで学習を止めました。
AplhaGoは2840万盤面に対して学習しaccuracyが57%だったそうです。
モデルの訓練で苦労したところと対策
最初の頃は、モデルの訓練を12時間もしたもののAccuracyが0.25程度にとどまり、実際に対戦しても弱々でどうしたものかと思っていました。
原因を調べたところ、次のような問題が見つかりました。
- 棋譜データから盤面を展開する処理にバグがあった。このため間違った盤面を学習させていた
- モデルのPermuteの指定方法が間違っていた。これによって、おかしな画像を学習させていた
- Bias層の後で、reshapeして(8,8)にしてしまっていた。8分類問題になってしまっていた
ディープラーニングは、意味のないデータを読み込ませてもなんとなく答えを出してしまうので、間違いがあることに気づきにくいです。また、処理の途中の状態を抜き出してチェックしても、それが正しいのか間違っているのかは判断しづらいです。
そこで、次のような手順で調査をしました。
1. ディープラーニングの出力の質に対する基準を設定する
今回は「私に勝つ」ということが基準でした。Accuracy(正確さ)についての基準値も設定しました。Accuracyが0.25というのは他の方のオセロAIに比べても低いので、他の事例から推測して少なくとも0.35は超えてほしいと考えていました。
逆に言うとこのような基準がないと調査することもなかったので、上のような問題は見つけることが出来なかったと思います。
2. モデルの問題の原因となりうる箇所をMECEに分類しておく
大分類としてはデータ、モデル、パラメータがあります。これらをツリー状に整理した上で、ツリーの枝を1つ1つを掘り下げていきます。
これを意識しないで手当たりデータや実装を差し替えたりすると、どこまでが正しくてどこからがおかしいのか、というように範囲を狭めることができなくなってしまいます。
3. データ加工からモデルの出力までの全体を少しずつ細分化して原因を見つける
2.と同じような話ですが、こちらはデータの流れに注目して細分化していきます。
例えば、ニューラルネットにすべて0などの単純な値を入力してみて、特定の層の出力を確認してみるといったことをすると、問題に気がつくことがあります。(全くわからないことの方が多かったですが...)
AIに打ち手を予想させてみる
学習が終わったら、打ち手の予想ができる状態になっています。試しに予想してみましょう。
# オセロの初期の盤面データを与える
board_data = np.array([[
[[0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0],
[0,0,0,0,1,0,0,0],
[0,0,0,1,0,0,0,0],
[0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0]],
[[0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0],
[0,0,0,1,0,0,0,0],
[0,0,0,0,1,0,0,0],
[0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0]]]],dtype=np.int8)
# 打ち手を予想する
model.predict(board_data)
# 出力結果
# array([[2.93197723e-11, 1.42428486e-10, 7.34781472e-11, 2.39318716e-08,
# 1.31301447e-09, 1.50736756e-08, 9.80145964e-10, 2.52176102e-09,
# 3.33402395e-09, 2.05685264e-08, 2.49693510e-09, 3.53782520e-12,
# 8.09815548e-10, 6.63711930e-08, 2.62752469e-08, 5.35828759e-09,
# 4.46924164e-10, 7.42555386e-08, 2.38477658e-11, 3.76452749e-06,
# 6.29236463e-12, 4.04659602e-07, 2.37438894e-06, 1.51068477e-10,
# 1.81150719e-11, 4.47054616e-10, 3.75479488e-07, 2.84151619e-14,
# 3.70454689e-09, 1.66316525e-07, 1.27947108e-09, 3.30583454e-08,
# 5.33877942e-10, 5.14411222e-11, 8.31681668e-11, 6.85821679e-13,
# 1.05046523e-08, 9.99991417e-01, 3.23126500e-07, 1.72151644e-07,
# 1.01420455e-10, 3.35642431e-10, 2.22305030e-12, 5.21605148e-10,
# 5.75579229e-08, 9.84997257e-08, 3.62535673e-07, 4.41284129e-08,
# 2.43385506e-10, 1.96498547e-11, 1.13820758e-11, 3.01558468e-14,
# 3.58017758e-08, 8.61415117e-09, 1.17988044e-07, 1.36784823e-08,
# 1.19627297e-09, 2.55619081e-10, 9.82019244e-10, 2.45560993e-12,
# 2.43100295e-09, 8.31343083e-09, 4.34338648e-10, 2.09913722e-08]],
# dtype=float32)
出力結果は、マスごとの配列なので、最大値をとると打ち手を取得することができます。
np.argmax(model.predict(board_data))
# 出力結果
# 37
左上から37番目が最善手のようですね。
最後に
いずれ、その2を書きたいと思います。
その2は、iOSデバイス上での動作となります。ディープラーニングをiOSデバイスで動作させる方法や、ミニマックス法やモンテカルロ木探索を取りれようとして失敗した話などを書こうと思います。
(書かなかったらすいません)
また、NoteではiOS開発、とくにCoreML、ARKit、Metalなどについて定期的に発信しています。
https://note.com/tokyoyoshida
Twitterでも発信しています。
https://twitter.com/jugemjugemjugem


