先に成果から
判定をミスった画像
判定精度は99.58%
10,000枚のテストデータセットのうち42枚がエラーとなりました。
画像の下にセンタリングされている数字が正解ラベル。その下に左寄せで5つ表示されている数字は尤度が高い順に並んだ予想。
尤度に比例した棒グラフが表示されますが、殆どのケースで尤度が低すぎて棒グラフになっていません。
多くのものは正解が2番めの尤度(第2候補)になっています。
しかし、右上の3枚のように正解が5番目(第5候補)までに入らないほど酷くハズしてしまうこともあるようです。
数字別に最も尤度が高かった画像
500Epochの学習後に行ったテストにて、数字別に最も尤度が高かった画像を抽出しました。
換言すれば「最も自信を持って正解した画像」と言って良いと思います。
でも「最もそれらしい」と言うよりは「他に似ていない」ものが選ばれている感もありますが...
特に6は「これが一番6らしい」と言われてもピンと来ませんね...
7には横棒が入ってるし...
経緯
VGG19を使うことやエラー画像を集めることが主目的ではありませんでした。
いずれ「収束性能を上げるいくつかの方法」なるテーマで記事を書いてみようかと思っております。そのためにまずは収束に時間がかかる大きな(深い)ネットワークを用いたサンプルを用意しておきます。
VGG19とは
詳細はこちらの論文に記載されておりますが...
VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION
ほとんどの方がご存知でしょうから説明する必要もありませんが、画像認識の世界的なコンペティションであるILSVRC2014にてClassification+localization分野の第一位を獲得したモデルです。
State of the artな世界はDeepなだけでなくWide and Deepな方向に進化を続けており、さらに多くのケースでは高度なArgumentation(データの前処理)を併用しています。
VGG19ではこれらの比較的新しい手法を用いておらず、単純にDeepにしただけのネットワークの集大成と言えます。
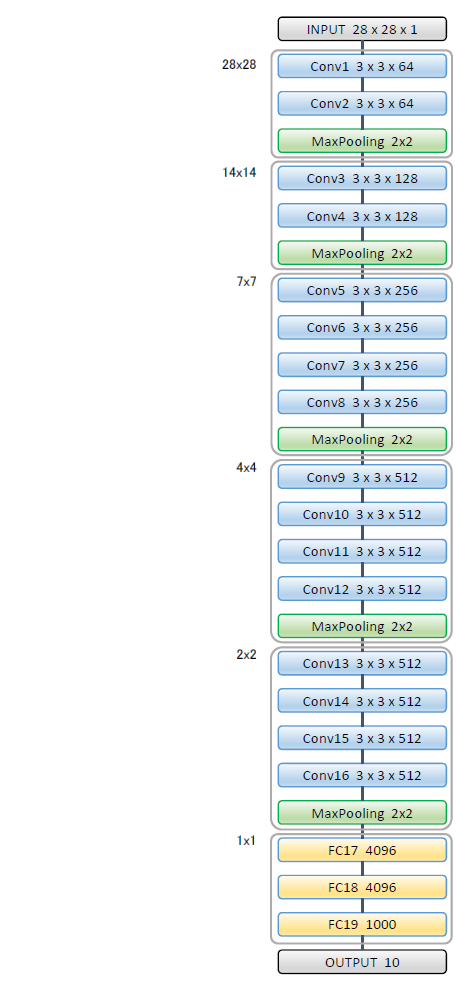
NetworkArchitecture
VGG19の名の通りWeightを持つ層が19層存在します。
19層のうち16層はConv層となっており、MaxPoolingにより5つのブロックに別れています。
詳細は前述の論文3ページ目のTable 1: ConvNet configurations最右列にある"E"が該当します。
図の左側に記載してある数値はPooling後に残るInput(画像)のサイズです。全てのPoolingはStrideが2x2に設定されているため、Poolingごとにサイズは1/2になります。
計5回のPoolingを実施しているため最終的には、最初の1/32のサイズになります。(2Dですので正しくは1/1024)になります。
Poolingは次元削減などとも呼ばれますが、784次元あった入力ベクトルが1次元まで削減されてしまいます。
MNISTで使えるのか?
VGG19はImageNet(224x224x3)の画像をターゲットとして開発されています。
しかしMNISTのデータセットは28x28x1となっており、ImageNetと比較するとかなり小さな画像になっています。
それを5段もPoolingしてしまうと...
28 / (2**5) = 0.875
縦横ともに1x1の情報も残っていません。もはや画像ではなく点ですね。実際には3回目のPoolingで切り上げられているため、辛うじて1x1の情報が残りますが、FC層への入力は1x1の極小サイズが512枚(Conv最終段のフィルタ数)になります。
なんとか学習してくれるかな、と思いつつ事例を探していると身近なところに良い記事が。
TensorFlow Expertを超えて
こちらの記事ではVGG16をベースにPoolingが4回になるよう、最終ブロックをカットする工夫が見られます。
前述の論文3ページ目のTable 1: ConvNet configurationsにある"D"をベースにConv層後の3層とMaxPoolingをカットされているようです。
記事によれば最終的には99.55%の認識率を達成しておられるので、VGG19をそのまま使っても近い成果が得られることを期待します。
VGG19のパラメータ(Weight)総数
| Layer | Kernel (W) | Kernel (H) | Input Channel | Output Channel | Parameters |
|---|---|---|---|---|---|
| Conv1 3x3x64 | 3 | 3 | 1 | 64 | 576 |
| Conv2 3x3x64 | 3 | 3 | 64 | 64 | 36,864 |
| Conv3 3x3x128 | 3 | 3 | 64 | 128 | 73,728 |
| Conv4 3x3x128 | 3 | 3 | 128 | 128 | 147,456 |
| Conv5 3x3x256 | 3 | 3 | 128 | 256 | 294,912 |
| Conv6 3x3x256 | 3 | 3 | 256 | 256 | 589,824 |
| Conv7 3x3x256 | 3 | 3 | 256 | 256 | 589,824 |
| Conv8 3x3x256 | 3 | 3 | 256 | 256 | 589,824 |
| Conv9 3x3x512 | 3 | 3 | 256 | 512 | 1,179,648 |
| Conv10 3x3x512 | 3 | 3 | 512 | 512 | 2,359,296 |
| Conv11 3x3x512 | 3 | 3 | 512 | 512 | 2,359,296 |
| Conv12 3x3x512 | 3 | 3 | 512 | 512 | 2,359,296 |
| Conv13 3x3x512 | 3 | 3 | 512 | 512 | 2,359,296 |
| Conv14 3x3x512 | 3 | 3 | 512 | 512 | 2,359,296 |
| Conv15 3x3x512 | 3 | 3 | 512 | 512 | 2,359,296 |
| Conv16 3x3x512 | 3 | 3 | 512 | 512 | 2,359,296 |
| FC1 4096 | 512 | 4096 | 2,097,152 | ||
| FC2 4096 | 4096 | 4096 | 16,777,216 | ||
| FC3 1000 | 4096 | 1000 | 4,096,000 | ||
| (合計) | 42,988,096 | ||||
| ※Biasは計算から除外しています | |||||
| ※厳密には最終段にSoftMax用の1000x10のWeightが存在します |
VGG19の論文ではパラメータ総数は144Mと紹介されていますが、MNISTで使用すると43M程度になります。
ImageNet(224x224x3)=144MとMNIST(28x28x1)=43Mのパラメータ数の差について
Conv1層の入力チャネル数
軽微な差ですがImageNetはカラーなのでConv1層への入力が3チャネルになっています。
FC1層への入力チャネル数
VGG19の論文と比較し100Mもの差が発生している原因はFC1層のInputが大きく異ることによります。
MNISTは28x28ですので前述の通り、5回のPoolingで1x1になってしまいます。しかしImageNetは224x224ですので5回Poolingしても7x7となるため、MNISTと比較すると49倍に達します。
この差がそのままFC1層への入力チャネル数となるため、FC1層への入力だけで100Mもの差が生じています。
実行結果
赤線は出来るだけ論文に忠実に実装したVGG19 (LearningRate = 5e-5)
青線はTensorFlowのExampleであるDeep MNIST for Experts (LearningRate = 1e-3)
Accuracy
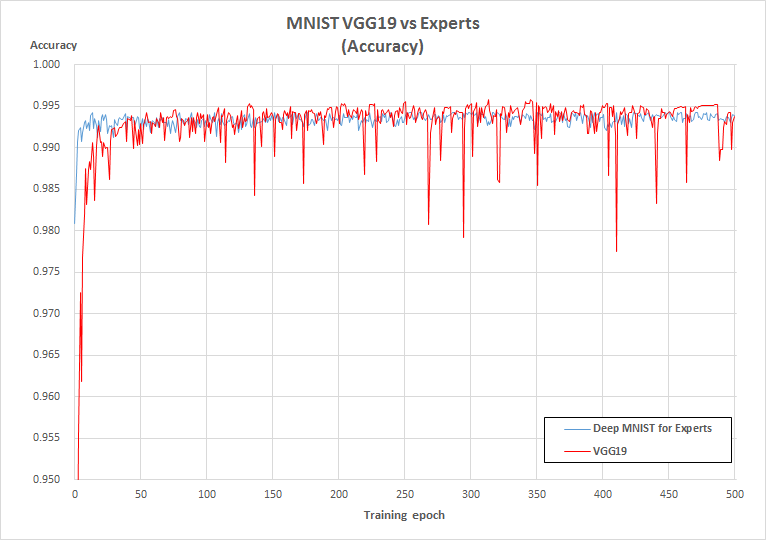
VGG19は314Epoch(16,430Sec)で記録した99.58%が最高精度
Deep MNIST for Expertsは79Epoch(289Sec)で記録した99.44%が最高精度
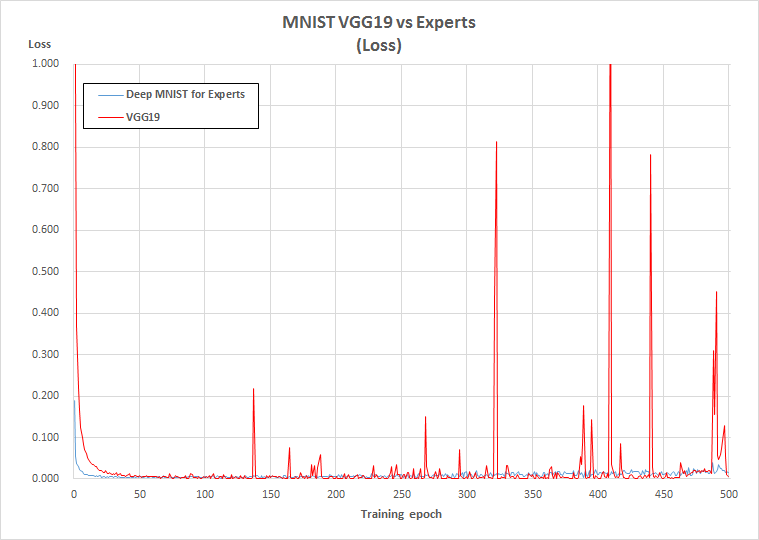
Loss
Accuracy、LossともにVGG19ではたまに急激な悪化が発生しています。
原因はLearningRateを限界まで高めたためと考えられます。
(今回はLearningRate=5e-5としていますが6e-5では学習が進みませんでした)
Deep MNIST for ExpertsのOptimizer設定について
| Optimizer | Learning Rate | Remark | |
|---|---|---|---|
| TensorFlow公式Exampleの実装 | SGD | 1e-2 | Decayあり |
| 今回の試験で用いた実装 | Adam | 1e-3 | Decayなし |
収束に要する時間
GPUにNVIDIA GeForce GTX1080を使用して500Epochの学習時間は下記の通りとなりました。
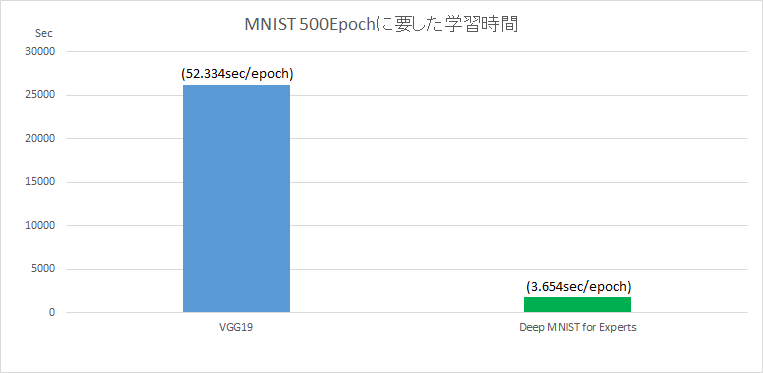
VGG19 26,167Sec (52.334sec/epoch)
Deep MNIST for Experts 1,827Sec (3.654sec/epoch)
500Epochまでの処理時間は約14倍となりました。
また最高精度に達するまでの時間を比較すると、VGG19は約57倍もの処理時間を要しています。
ソースコード
TensorFlowにてVGG-19を実装したサンプルをGitHubに用意致しました。
Python3系専用コードですが宜しければお試しください。
まとめ
CNN2層(FC層と合わせて3層)のDeep MNIST for Expertsと
CNN16層(FC層と合わせて19層)のVGG19を比較してみました。
最高精度では99.44% vs 99.58%と大きな差になったものの、
最高精度到達までの学習時間は57倍にもなってしまいました。
VGG19ではLearningRateをほぼ限界まで高く設定し学習時間の短縮を試みましたが、それでも7時間を超えてしまいました。
近いうちに「学習時間を短縮する」をテーマにした記事を書いてみたいと思います。
お付き合いありがとうございました。